2. 江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003;
3. 江苏科技大学 土木工程与建筑学院,江苏 镇江 212003
2. Jiangsu University of Science and Technology, Naval Architecture and Ocean Engineering School, Zhenjiang 212003, China;
3. Jiangsu University of Science and Technology, Civil and Architecture School, Zhenjiang 212003, China
海洋结构物的安全性目前受到的关注越来越多。由于海洋油气开采增多,所需要的海洋平台因此变多,导致船舶与海洋平台碰撞事故越来越多。Tebbet分析了世界上 100 起需要修理的海洋平台的损伤原因,认为近 25% 的平台损伤是由碰撞引起的。当发生碰撞事故时,会导致各方面巨大的损失,例如对环境的破坏,人员的伤亡,经济的损失等。因此为了减少碰撞损失,很有必要研究海洋平台的碰撞规律。
半潜式海洋平台是一种大部分浮体没于水面下的一种小水线面的移动式海洋平台,由平台本体、立柱和下体或浮箱组成。由于半潜式海洋平台在波浪上的运动响应较小,目前应用越来越广泛,在海洋工程中,不仅可用于钻井,其他如生产平台、铺管船,供应船、海上起重船等都可采用。本文研究分析供应船与半潜式海洋平台的碰撞过程。它是一个复杂的动力过程,涉及到的力学过程极为复杂。不但要考虑到平台结构自身的动力、材料特性,还要考虑到供应船的特征以及船舶与海洋平台周围流场的相互影响。所以,要精确计算碰撞的力学特性比较困难,目前大多采用有限元分析法。
本文采用Ansys/Ls-Dyna软件来模拟碰撞过程,其优点是非线性动力分析以及显示积分求解,研究供应船与半潜式平台碰撞后,平台的应力与应变变化,碰撞力变化以及能量转化,找出碰撞下的规律,为平台安全性方面设计提供建议。
1 碰撞模型船舶与海洋平台发生碰撞的部位有首碰、尾碰与侧碰。这 3 种情况下,侧碰对海洋平台的损伤最大,尾碰次之,首碰最小。因为侧碰时,船舶带动了较多的附连水,碰撞时的能量最大。根据文献[4, 16, 17],侧碰时,附连水质量系数取 0.4,首碰和尾碰时附连水质量系数取 0.1。本文中供应船正常工作重量为 8 000 t、平台总质量为 40 500 t,附连水使用附加质量法进行分析。
1.1 海洋平台参数及模型本文根据所提供的平台的CAD图纸,采用Ansys分别建立平台立柱、横撑和浮箱模型,并对碰撞区域的网格单独进行细化。
|
|
表 1 供应船主尺度 Tab.1 The dimension of supplier ship |
|
|
表 2 平台主尺度 Tab.2 The dimension of platform |
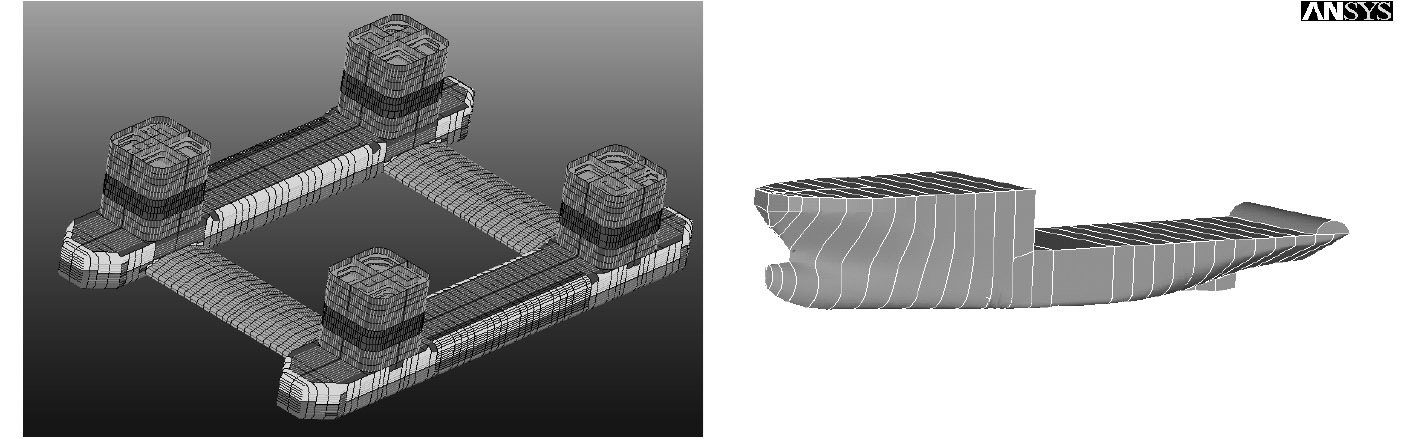
|
图 1 海洋平台及供应船的有限元模型 Fig. 1 The FEM model of both supplier ship and platform |
坐标标记为( X, Y, Z)笛卡尔坐标系。坐标原点取在平台中心处, X 轴重合于基线,向平台首部方向为正; Y 轴垂直于中线面,向右舷为正; Z 轴垂直于水线面向上为正。坐标以米为单位。本文中所用坐标系的示意图如图 2和图 3所示。
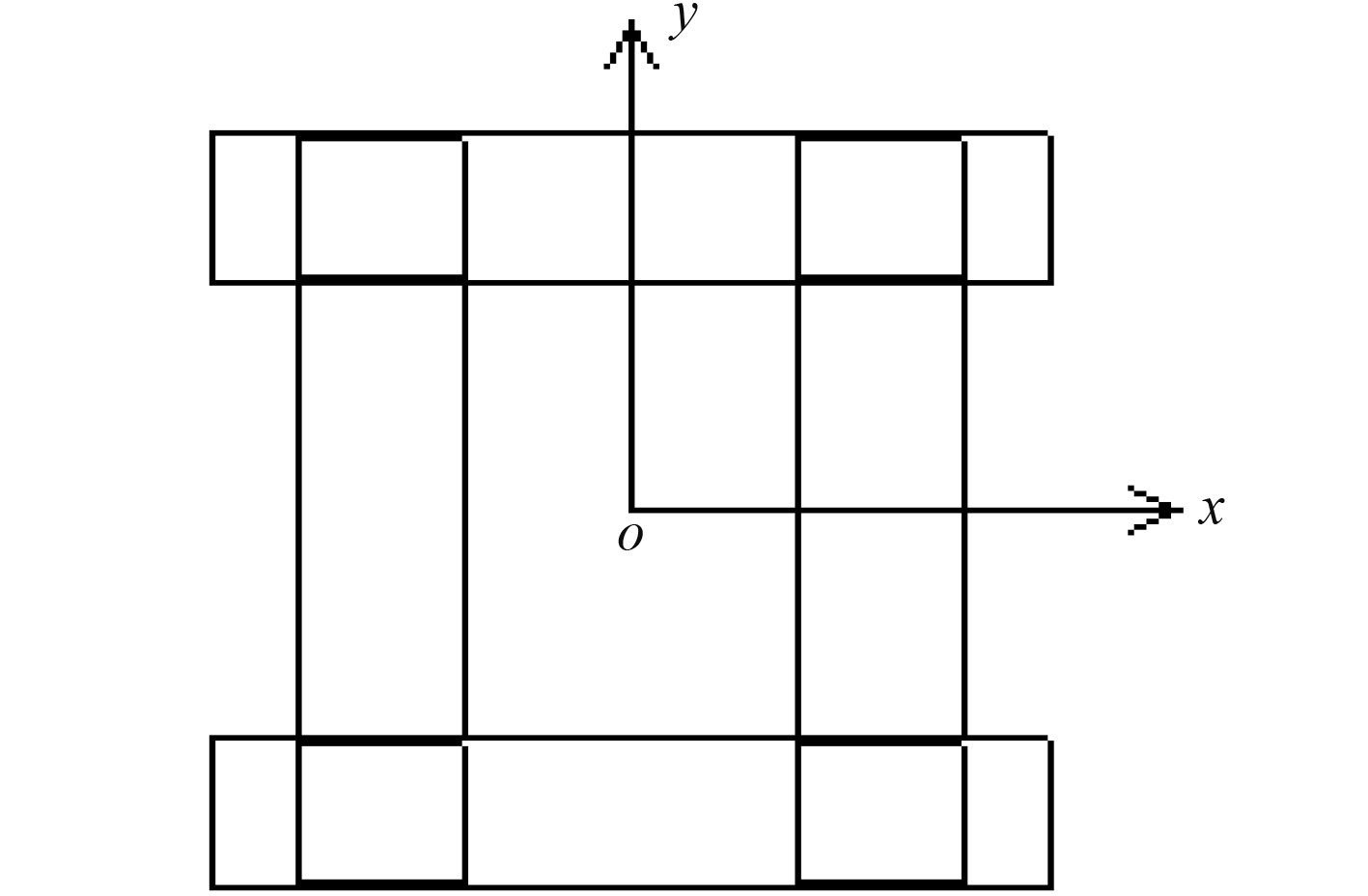
|
图 2 XOY 平面坐标示意图 Fig. 2 Schematic diagram of XOY plane coordinate |
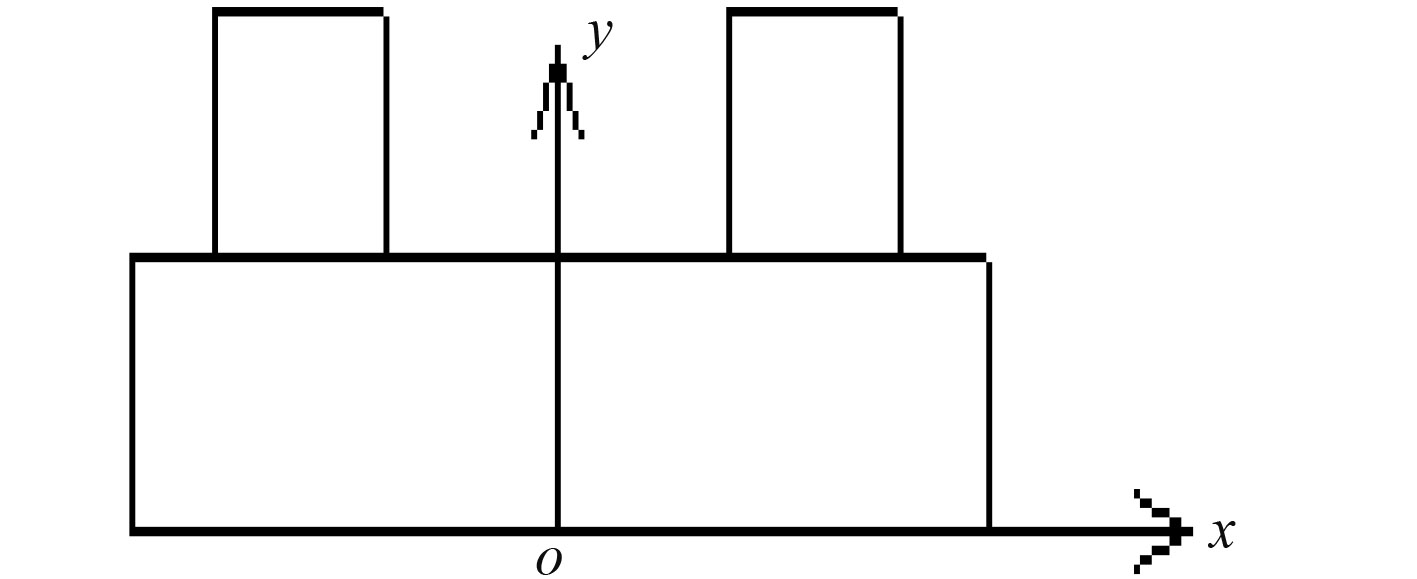
|
图 3 XOZ 平面坐标示意图 Fig. 3 Schematic diagram of XOZ plane coordinate |
供应船靠泊位置在平台首尾 2 个立柱之间,供应船靠泊时,以船尾靠向平台。所以供应船对平台可能的撞击位置为立柱外侧平面或立柱过渡处(分别称为正侧撞和角撞)以及横撑、下浮体构件。
1.3 边界条件本模型没有对平台上层建筑建模,与技术人员协商后,边界条件取平台立柱上端刚性固定[8 –9]。
2 船舶碰撞的简化算法假设:
1)碰撞区域两边对称,为矩形。
2)破坏产生在速度最小时(当速度为临界速度时,破坏产生在速度降为 0 的时候),所有的动能全部转化为破坏区域内的内能。若速度最小不为 0 时,这是动能碰撞前后的差量转化为破坏区域的内能。
E
0为弹性模量,
E
1为切线模量;
塑性应变能
| ${V_p} = \oint {E_0 \cdot \varepsilon_0} + \frac{1}{2}E_1 \cdot \varepsilon_1{\rm{d}}v{\text{;}}$ |
弹性应变能
| ${V_e} = \oint {E_0 \cdot \varepsilon_0} {\rm{d}}v{\text{;}}$ |
形函数一阶假设在塑性区域:
因此
| ${V_e} = \oint {E_0 \cdot \varepsilon_0} {\rm{d}}v = t \cdot 1 \cdot 2 \cdot \int_0^{a_0} {E_0} \frac{{\varepsilon_0\left( 0 \right) \cdot y}}{{a_0}}{\rm{d}}y = t \cdot 1 \cdot E_0 \cdot \varepsilon_0 \cdot a_0,$ |
所以
| $\begin{split}\\[-12pt]V = & t \cdot 1 \cdot E_0 \cdot \varepsilon_0 \cdot a_0 + t \cdot 1 \cdot a_1\left( {2 \cdot E_0 \cdot \varepsilon_0 + E_1 \cdot \varepsilon_1} \right)=\\[5pt]& t \cdot 1\left( {p_0 \cdot a_0 + 2p_0 \cdot a_1 + E_1 \cdot a_1 \cdot \varepsilon_1} \right){\text{。}}\end{split}$ | (1) |
计算下面这些数据得
| $\begin{array}{l}E_0 = 2.06{\rm E} + 11,\;\;\;\;\;E_2 = 2.06{\rm E} + 10, \;\;\;\;\;\varepsilon_1 = 1.72{\rm E} - 3,\\[5pt]t = 0.02,\;\;\;\;\;\;\;\;\;\;\;\;\;l = 6.18,\;\;\;\;\;\;\;\;\;\;\;\;\;P_0 = E_0\times \varepsilon_1 = 3.55{\rm E}+8\end{array}$ |
用Matlab线性回归得到的经验公式为:
| $\begin{array}{*{20}{l}}{p_1 = 1.014{\rm E}+9 = t*l*E_1*a_1 = 2.546{\rm E}+9,}\\[5pt]a_1 = 1.014/2.546 = 0.398,\\[5pt]{p_2 =-2.501{\rm E}+7 = t*l*p_0*\left( {2 + a_0} \right) = 4.388{\rm E}+7*\left( {2 + a_0} \right)} \\[5pt]a_0 =-2.57{\text{。}}\end{array}$ |
因为以塑性应变开始为正,所以弹性区域为负值,其绝对值为弹性区域大小。
| $V = t \cdot l\left( {E_1 \cdot a_1 \cdot \varepsilon_1 - 1.774p_0} \right){\text{。}}$ |
注意的是,式(1)或式(2)必须在产生塑性变形时使用。
如果碰撞区域有环肋,则环肋先于外板破坏,式(2)可修正为:
| $V = t \cdot l\left( {E_1 \cdot a_1 \cdot \varepsilon_1 - 1.774p_0} \right) + n \times A_0{\text{。}}$ |
式中: A 0 为环肋破坏吸收的能量; n 为破坏区域内的数量; A 0 可由实验确定。
由以上可知,当临界破坏能由公式无肋或有肋确定后,由假设 2 即可求得临界破坏船速。即
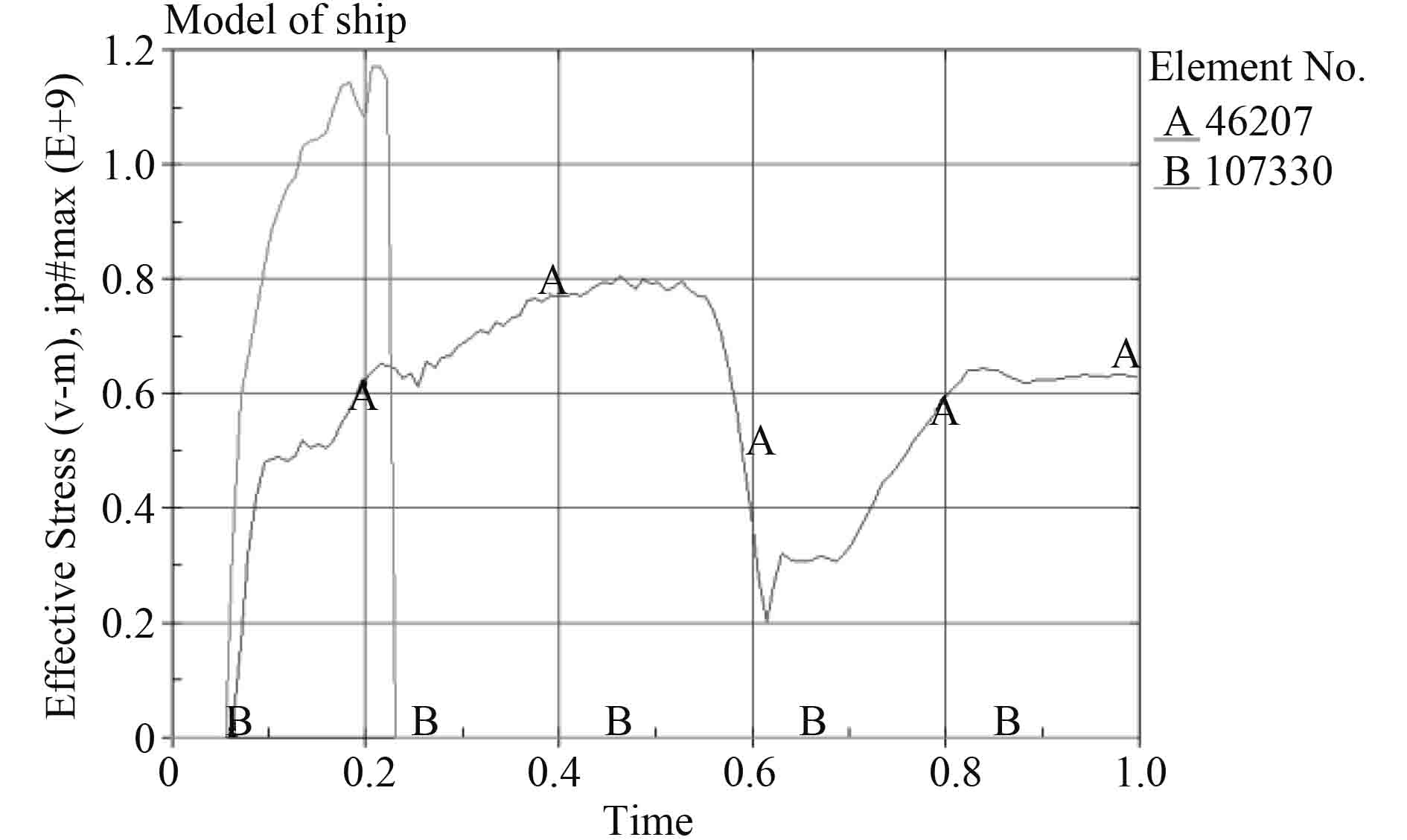
图 4~ 图 6为供应船船尾以 3 m/s速度下正碰平台立柱水平强框处应力、应变图以及能量时历图。
|
图 4 应力时程曲线 Fig. 4 Time history of stress |
|
图 5 应变时程曲线 Fig. 5 Time histiory of strain |
|
图 6 能量转换时程曲线 Fig. 6 The curve of exchange of potential energy and kinetic energy |
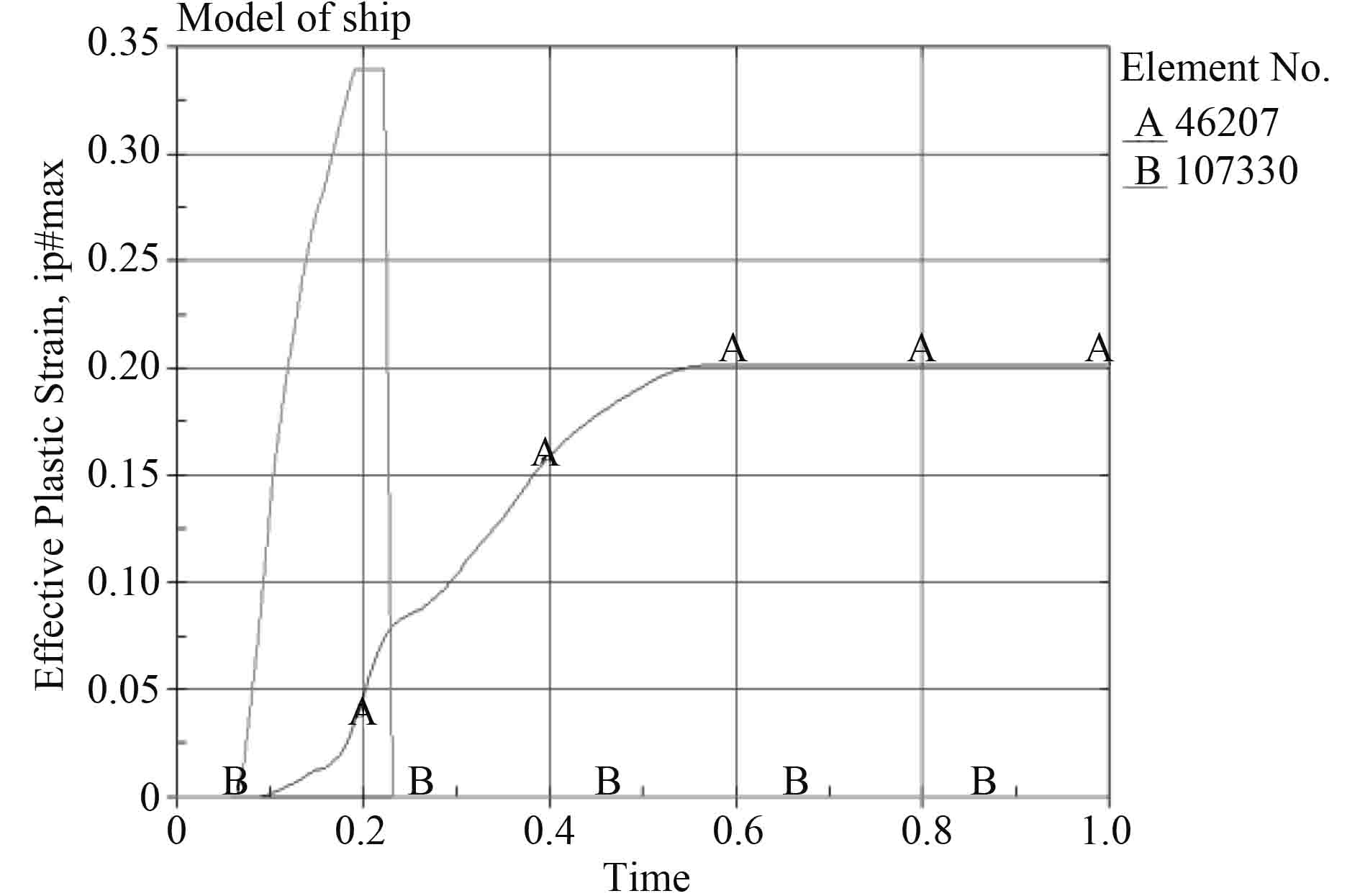
从应力、应变时历图中可看到,船尾与平台在 0.06 s时发生碰撞,碰撞刚开始时平台立刻发生变形,与此对应的是产生弹性应变,随着时间的推移,应力不断增大直到超出极限应力后,单元产生塑性变形,此时对应的应变图中为塑性应变。相应的,应力会进一步增大,其应力变化率刚开始时较大,因为刚开始时发生弹性应变,单元的应变率较大。之后,应力的变化率开始减小,因为此时发生塑性变形,此单元的应变率较小。
外板单元曲线到达 0.56 s时,应变不再增加,但是对应的应力却减小。可以得知碰撞已经结束,供应船往回弹,由于之后的变形为塑性变形,其不能恢复所以不发生变化,而弹性变形会减小,相应的应力也开始减小。
通过观察碰撞区域应变图可知,内部单元的应力和应变在 0.22 s同时变成 0。这说明内部单元在此时已经失效,观察其应变可知,此时,其塑性应变达到材料所定义的失效应变 0.34,单元自动失效[21]。并且根据应变时历曲线可知单元完全失效,外板单元在 0.56 s时达到稳定的应变状态,观其应变可知外板单元并未失效。
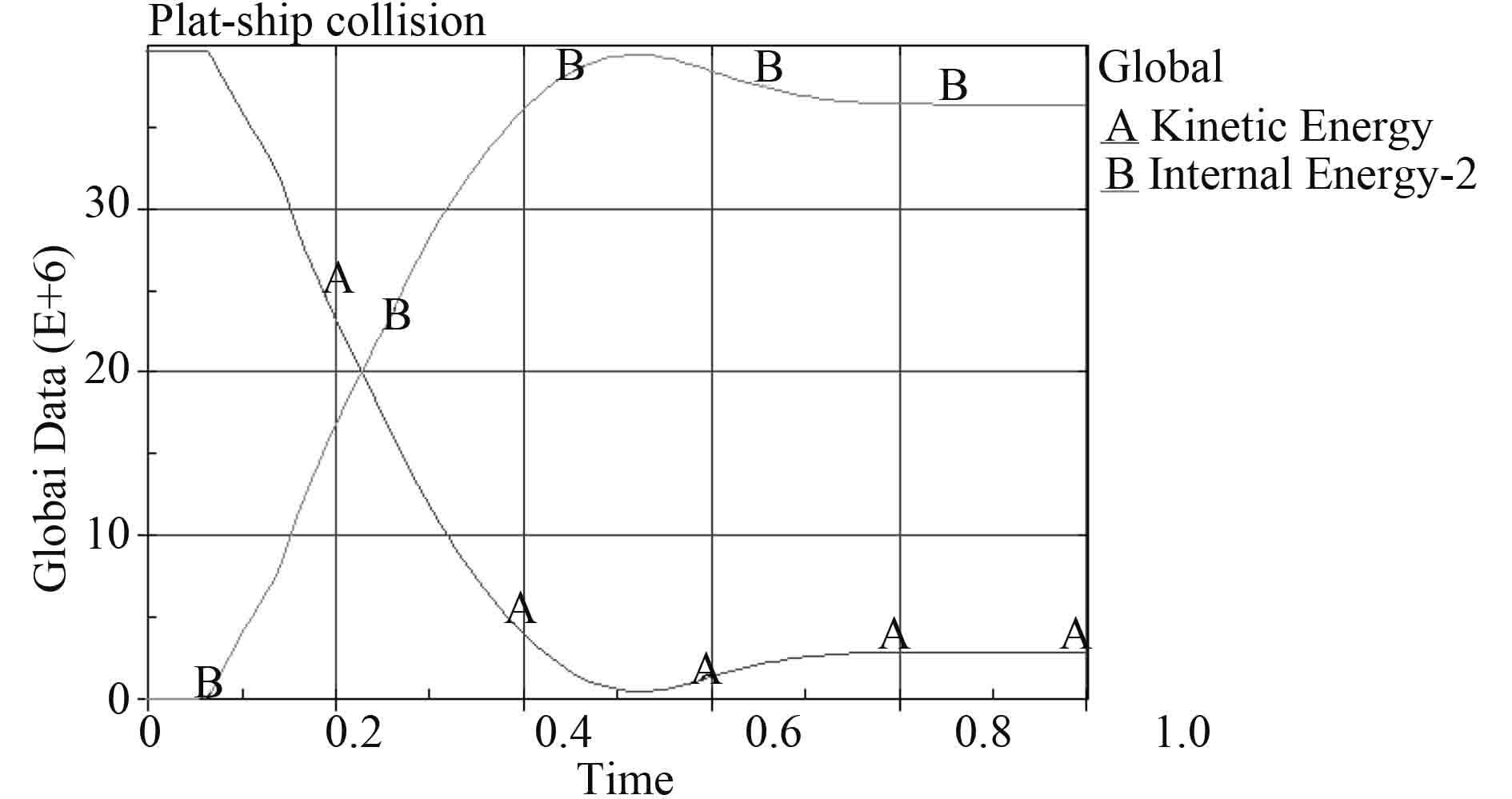
从能量时历图可看到,船舶的动能转化为平台的势能。碰撞过程中,船舶的动能急剧减小,平台的势能急剧增大。在大约 0.56 s时,平台的势能达到最大而船舶的动能达到最小,这表明船舶此时处于最大碰撞。再这之后,平台的势能略微减少,船舶的动能略微增加,说明碰撞达到最大值之后,平台对船舶产生反作用,使船向反方向运动。大约在 0.75 s,平台的势能与船舶的动能趋于稳定。
从图中可知,外板单元没有失效。通过读取能量曲线(internal energy),内部结构单元对应时间-能量点为
可知,外板单元并未破坏,所以船尾正碰平台立柱时,平台内部单元首先发生破坏,内部结构是指水平强框处单元,外板失效所需能量比内部结构失效所需能量大。
3.2 平台下浮体处碰撞分析图 7~ 图 9为供应船以 1 m/s的速度正碰下浮体上部过渡处的应力、应变以及能量时历图

|
图 7 应力时程曲线 Fig. 7 Time history of stress |
|
图 8 应变时程曲线 Fig. 8 Time histiory of strain |
|
图 9 能量转换时程曲线 Fig. 9 The curve of exchange of potential energy and kinetic energy |
从应力曲线可看到,供应船在 0.34 s时与平台碰撞,应力急剧增大,在 0.5 s时达到最大值,之后应力下降,说明供应船已经回弹,接着,应力在短时间内产生低频率的波动。
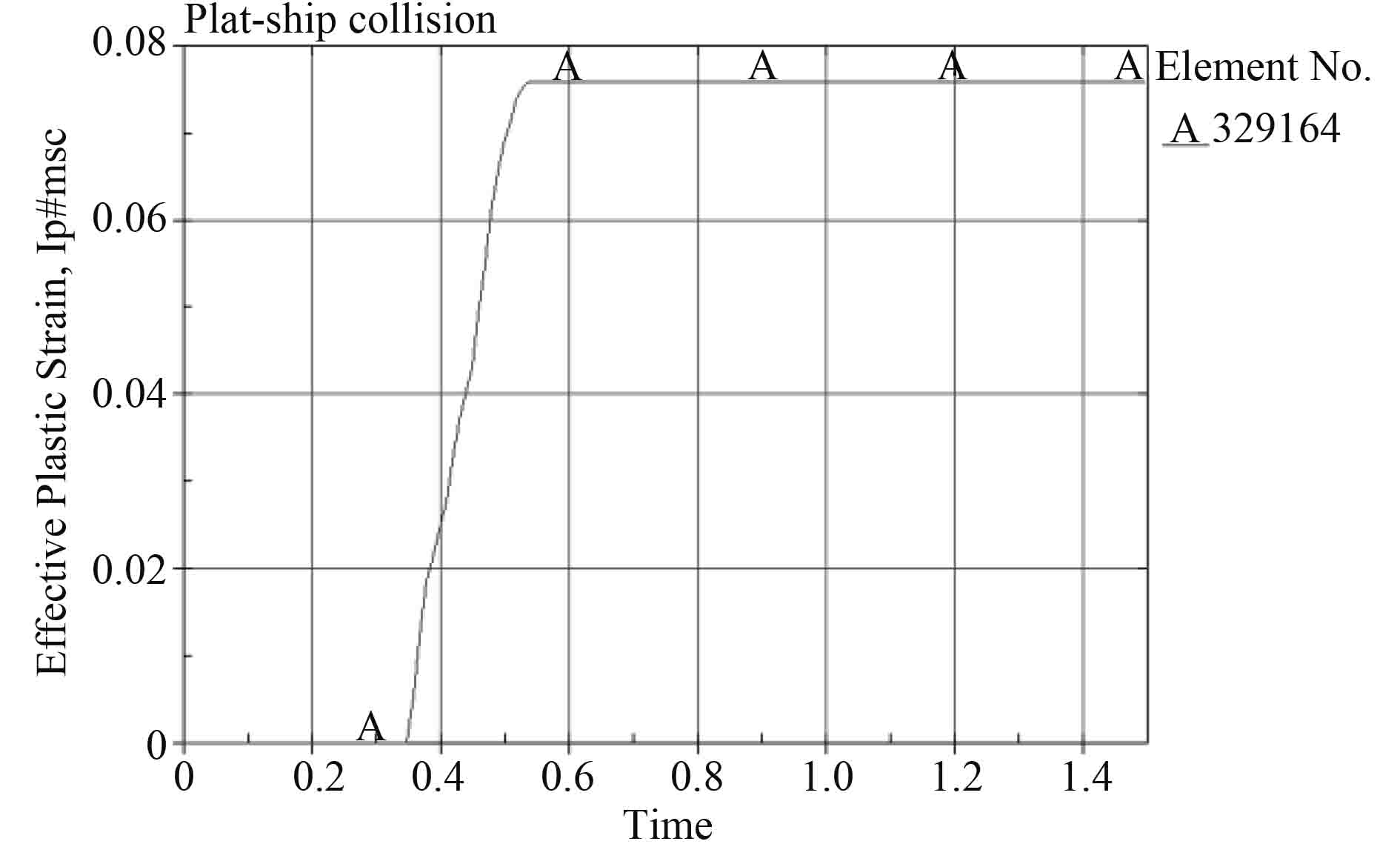
从应变曲线可看出,0.5 s之后,平台的应变不再变化,而应力却开始减小。可以知道碰撞已经结束,塑性变形由于不能恢复而不发生变化,弹性变形会减小,所以应力减小。图中最大应变为 0.076,小于材料的失效应变 0.34。单元没有被破坏。
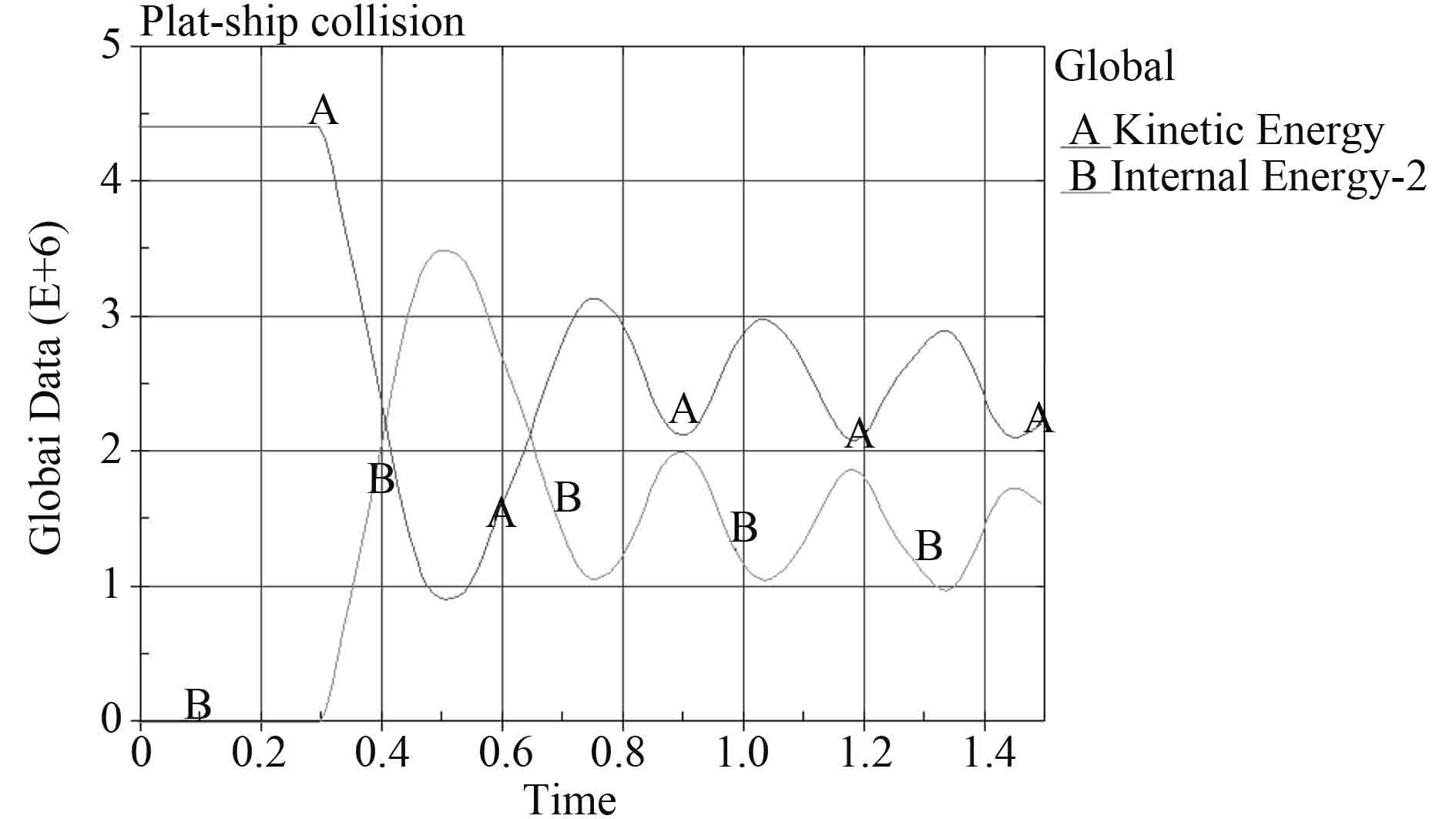
从能量图可看出,船舶的动能转化为平台的势能。大约在 0.4 s时,平台的势能和船舶的动能产生短时间的低频波动,船舶的动能与平台势能之和略小于船舶初始动能[18]。可以推测平台可能发生短时间内的低频振动。
4 结 语本文分析了供应船与半潜式平台的碰撞,得出了半潜式海洋平台在供应船尾碰撞下的应力、应变与能力交换的时程结果同时,通过这些计算,得出如下规律:
1)碰撞过程中正碰时内部结构单元首先发生破坏-此处内部结构是指水平强框处单元,外板失效所需能量比内部结构失效所需能量大。以上碰撞水平强框处时,可充分接触水平强框,导致水平强框先破坏。所以,水平强框起到了吸收能量,保护外板的作用。但水平强框间隔不宜过小,使得结构过强,进而使外板在被碰撞时直接破坏。
2)撞击位置的不同,能量转化也不一样。当撞击速度小于破坏速度时,单元没有破坏,当船回弹时,外板上的单元由于弹塑性材料及弹性应变的影响导致板单元产生“振动”过程,应力和能量产生短时间波动,但这种低速碰撞导致外板产生的低速低频振动,对于工作时的平台,会造成很大的影响,平台无法正常工作,是平台设计时应注意的一点。
| [1] | 龚顺风, 金伟良, 王全增. 海上固定平台受损构件的修理与评估[J]. 中国海洋平台, 2001, 16 (2): 37–41. |
| [2] | JIN Wei-liang, GONG Shun-feng, SONG Jian. Preliminary report of damage assessment analysis for some offshore Jacket platform[R]. Institute of structural Engineering, Zhejiang University, 2001(12). |
| [3] | 李润培, 陈伟刚, 顾永宁. 船舶与海洋平台碰撞的动力响应分析[J]. 上海交通大学学报, 1996, 30 (3): 40–48. |
| [4] | 胡永利, 林一, 谭美. 半潜式平台遭遇碰撞的结构响应分析[J]. 船舶与海洋工程, 2012, 88 (1): 46–55. |
| [5] | Shi Gen Lin, Shen Wei. Hybrid control of a parallel platform based on pneumatic artificial muscles combining sliding mode controller and adaptive fuzzy CMAC[J]. Control Engineering Practice, 2013, 21 (1): 76–86. DOI: 10.1016/j.conengprac.2012.09.010 |
| [6] | Morales C, Gardin S, Schnyder J, et al. Berriasian and early Valanginian environmental change along a transect from the Jura Platform to the Vocontian Basin[J]. earthquake engineering, 2013, 60 (1): 36–63. |
| [7] | 孙彦杰, 李良碧, 尹群. 碰撞、爆炸灾害下海洋平台风险评估研究初探[J]. 中国海洋平台, 2007, 22 (5): 38–47. |
| [8] | 陈铁云, 朱正宏. 海洋平台碰撞和损伤分析的进展[J]. 力学进展, 1989, 19 (4): 454–463. DOI: 10.6052/1000-0992-1989-4-J1989-053 |
| [9] | HYSING T. Damage and penetration analysis-safety of passenger ROR vessels[J]. DNV Report, 1995: 95-0419, Norway. |
| [10] | JOAO G, LIVERIA D O. The behavior of steel offshore structures under accidental collision[C]// Proceeding of 13th annual offshore technology conference. OTC4136, 1981: 187–198. |
| [11] | 金伟良, 龚顺风, 等. 大型船舶碰撞引起的海洋导管架平台结构损伤分析[J]. 海洋工程, 2003, 21 (2): 20–25. |
| [12] | 吴卫国, 朱孟巍. 船舶与海洋平台碰撞的动力特性研究. 武汉理工大学论文, 2006(4): 19-24, 28–36. |
| [13] | BrOWN A, TECH V, TIKKA K, et a1.Structrual design and response in collision and grouding[C]// The Society of Naval Architects and Marine Engineers, 2000 Annual Meeting Preprings, 2000. |
| [14] | Kim J Y, Yu E, Kim D Y, et al. Long term monitoring of wind induced responses of a large span roof structure[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99 (2011): 963–995. |
| [15] | 李上明. 冲击波作用下水下结构载荷计算方法[J]. 工程力学, 2014, 31 (12): 11–18. |
| [16] | 秦立成. 海洋导管架平台碰撞动力分析[J]. 中国海上油气, 2008, 20 (6): 416–422. |
| [17] | 王林, 周国宝, 米旭峰. 基于整体海洋平台模型的下落物体撞击数值仿真[J]. 解放军理工大学学报(自然科学版), 2008, 9 (6): 687–694. |
| [18] | Calautit J K, O’Connor D, Hughes B R. Determining the optimum spacing and arrangement for commercial wind towers for ventilation performance[J]. Building And Environment, 2014, 82 (2014): 274–287. |
| [19] | 刘雄, 梁湿. 风力机翼型动态失速气动特性仿真[J]. 工程力学, 2015, 32 (03): 203–211. |
| [20] | Bing-bing S, Xiao-ying S, Yue W. Multi-object optimization of membrane structure based on Pareto Genetic Algorithm[J]. Journal of Harbin Institute of Technology, 2010, 17 (5): 622–630. |
| [21] | 刘平, 王林. LS-DYNA软件对某半潜式海洋平台发生碰撞的分析[J]. 解放军理工大学学报(自然科学版), 2015, 10 (16): 465–470. |
 2017, Vol. 39
2017, Vol. 39
