0 引　言

多用途船往往是肥大型船，不仅能满足大型货物的运输，同时还能满足其他应急任务。由于单一用途的船舶具有一定的局限性，多用途船是一种发展趋势，因此研究多用途船很有必要，特别是随着如今绿色节能的推广，船舶的阻力性能研究也越发重要。

在船舶的初步设计中，船舶的主尺度及其型线只是初步确定，利用数值模拟，对船型的阻力性能进行预报，为接下来的船型优化研究提供一定的借鉴。

国内近年来运用CFD软件计算船舶阻力特性的研究层出不穷，王金宝等^[1]对低速肥大型船KVLCC2M进行了阻力性能预报，并且对尾流场进行了数值模拟，同时将其方法应用于其他实船，结果比较吻合。倪崇本^[2]利用Fluent软件，通过粘性流的叠模算法求得粘性阻力，用Euler方程在理想流下求得兴波阻力，实现了对高速船的阻力预报，并对多体船进行了预报，获得了较好的结果。刘英良^[3]对超大型集装箱船进行了研究，通过shipflow软件对船的最优方形系数、球首的选择和尾部伴流场进行研究，对超大型集装箱船的设计优化提供了很好的依据。王健^[4]利用Fluent软件对海洋管道、高速单体船和高速三体船进行了数值模拟，计算了各阻力并分析了各流场变化，为多体船和海洋工程的研究做出了贡献。

总的来说，CFD模拟会渐渐成为研究船舶阻力性能的主流。为了能够准确快速的对船舶总阻力进行预报，本文将CFD数值模拟与三因次法相结合，采用Solidworks三维软件对船舶进行三维建模，应用CFD理论进行数值模拟计算，得到对应航速下船模的总阻力值系数，根据普鲁哈斯卡假设和三因次方法，利用最小二乘法拟合形状系数，进而计算出实船的总阻力。

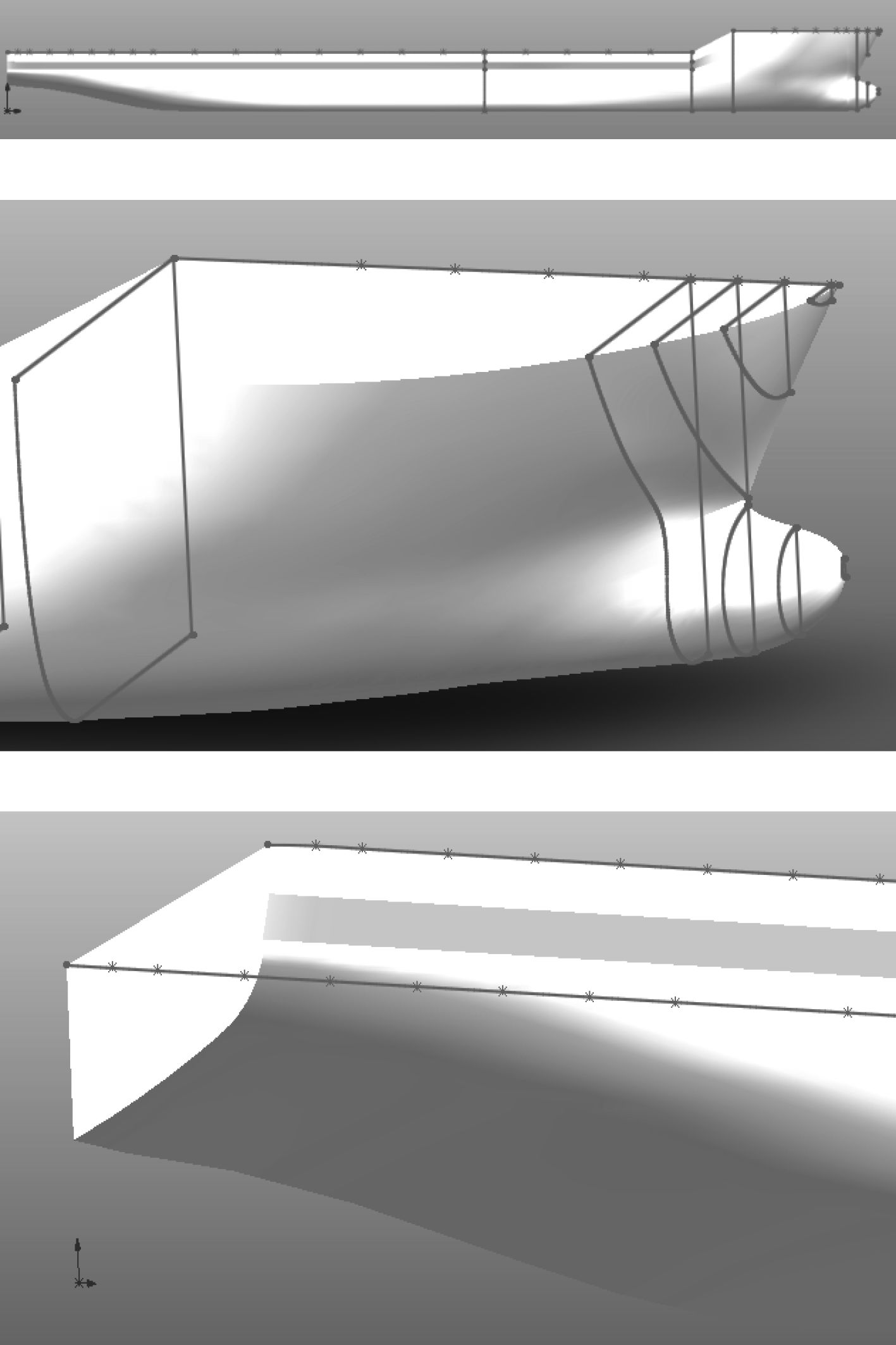
1 数值模拟分析 1.1 模型建立

某肥大型多用途低速船舶主要尺度要素如表 1所示。因为该船具有对称性，在Solidworks^[5]中分站后导入横剖线，通过放样命令，生成光顺的半船模型，如图 1所示。

1.2 网络划分

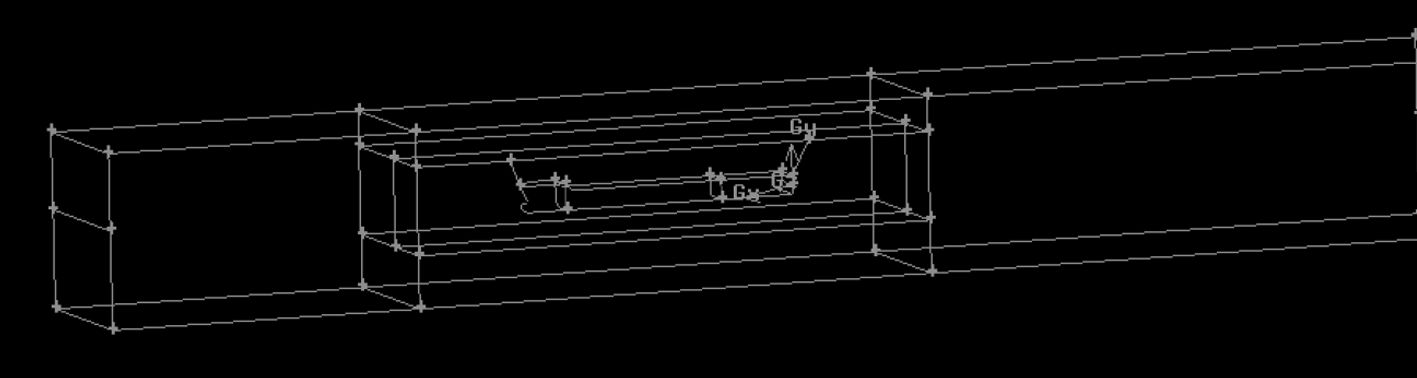
创建1个 800 m × 100 m × 100 m的方形流域，离船首大约1个船长，船尾大约 3 个船长，随后将流域划分为 6 个区域，以设计水线划分流域的进出口，如图 2所示。

为了保证精度及计算速度，船体附近的网格要做加密处理，这也是模拟计算的重点，而且船体表面的曲率变化挺大，需要使用非结构化网格（俗称四面体网格）；相反稍远的地方不需要过密的网格，而且运用非结构化网格会加大计算量，增加计算时间，考虑到实际的硬件设施，故采取结构化网格，且间距可以稍微调大些。这样既保证了计算需求，又大大的减少了计算的时间^[6]。

中间非结构网格采取了Size Function，以 1.3 的比率沿船体表面向外均匀扩散，生成网格之后对网格进行了检查，共生成了 1 021 377 个网格，中间区域有 845 109 个网格，角度倾斜率没有超过 0.95 的，如图 3所示。

1.3 计算参数和边界条件

将划分好的网格msh文件导入Fluent中，首先对船体进行了缩尺，缩尺比为 50，实船与船模主要参数如表 2所示。

其他参数设置如下^{[7 –8]}：

1）选择非稳态数值模拟。

2）选择多相流模型VOF。

3）湍流模型选择RNG $k - \varepsilon $ 模型，采用标准壁面函数。

4）液体材质选择水。将水的密度改为 $\rho = 1\;025\;{\rm{kg}}/{{\rm{m}}^3}$ ，运动粘度 $\nu = 1.053\,\,72\; \times \;{10^{ - 6}}\;{{\rm{m}}^2}/{\rm{s}}$ ，模拟在 20 ℃ 时，海水的密度和运动粘度。

5）大气压的参考点定义在空气域中，重力加速度 $g = 9.81\;{\rm{m}}/{{\rm{s}}^2}$ 。

6）边界条件。空气入口和海水入口设置为速度入口；空气出口和海水出口设置为压力出口，这里需要使用自定义函数（User-Defined Function，UDF），控制出口处的压强分布，水线以下的相对压强随着水深的增加变化，水线以上的相对压强为 0；船中设置为对称面；流域边界设置为Moving Wall，且速度与流域速度一致。

7）离散方法选SIMPLE，离散格式均选 2 阶迎风格式。

8）初始化后捕捉正确海水和空气两相。

9）设置残差监视器。残差收敛标准定为 10 ^–5，阻力监视器监视船体阻力收敛曲线，受力方向沿船长方向，为 X 轴。

10）设置迭代计算。设置时间步长和总步数。时间步长设置为 0.001，这里的总时间用流域的总长度除以模拟的航速，总时间又等于时间步长乘以总步数，这样便能设置相应航速下的总步数，最后设置每1步迭代 20 次。

2 阻力计算

实船船体阻力计算采用三因次法^[9]。认为粘压阻力系数 ${C_{pv}}$ 与摩擦阻力系数 ${C_f}$ 之比为常数 k，即

$k = \frac{{{C_{pv}}}}{{{C_f}}}\text{，}$

(1)

实船总阻力系数为：

${C_{ts}} = (1 + k){C_{fs}} + {C_{ws}} + \Delta {C_f}\text{，}$

(2)

船模的总阻力系数为：

${C_{tm}} = (1 + k){C_{fm}} + {C_{wm}}\text{，}$

(3)

又因：

${C_{wm}} = {C_{ws}}\text{，}$

(4)

故实船总阻力系数为：

$\begin{array}{l}{C_{ts}} = (1 + k){C_{fs}} + {C_{wm}} + \Delta {C_f}= \\\quad \, (1 + k)({C_{fs}} - {C_{fm}}) + {C_{tm}} + \Delta {C_f}\text{。}\end{array}$

(5)

其中（1 + k）形状因子可通过普鲁哈斯卡的假设求得。普鲁哈斯卡认为傅汝德数在 0.1～0.2 之间时，可近似认为兴波阻力 ${C_{wm}}$ 与傅汝德数 ${F_r}$ 的4次方成正比关系。故式（5）可表示为：

$\frac{{{C_{tm}}}}{{{C_{fm}}}} = (1 + k) + b\frac{{F_r^4}}{{{C_{fm}}}}\text{。}$

(6)

通过线性拟合可求得（1 + k）值。

摩擦阻力系数可用 1957ITTC公式计算：

${C_f} = \frac{{0.075}}{{{{\left( {{\rm{lg}}Re - 2} \right)}^2}}}\text{，}$

(7)

式中：雷诺数 $Re = \displaystyle\frac{{v{L_{wl}}}}{\nu }$ ， v 表示航速， ${L_{wl}}$ 表示水线长， v 表示水的运动粘性系数，取海水在 20 ℃ 时的运动粘度， $\nu = 1.053\,\,72 \times {10^{ - 6}}{{\rm{m}}^2}/{\rm{s}}$ ； ${\rm{\Delta }}{{{C}}_{{f}}}$ 表示粗糙度补贴系数，通常取 0.4 × 10 ^–3，也可用ITTC推荐的公式：

$\Delta {C_f} = [105{(\frac{{{k_s}}}{{{L_{wl}}}})^{\frac{1}{3}}} - 0.64] \times {10^{ - 3}}\text{，}$

(8)

式中 ${k_s}$ 通常取 150 × 10 ^–6（m）。

因此实船总阻力为：

${R_{ts}} = \frac{1}{2}{\rho _s}{v_s}^2{S_s} \cdot {C_{ts}}{\rm{}}\text{。}$

(9)

3 结果及分析

本文模拟了船舶在 6 kn，8 kn，12 kn（设计航速），13 kn，14 kn，15 kn，16 kn这 7 个航速下的运动状态，模拟速度分别为 0.436 m/s，0.582 m/s，0.873 m/s，0.946 m/s，1.018 m/s，1.091 m/s，1.164 m/s。当流体流完整个流域，残差收敛达到要求，阻力监视器监测的阻力变化不大，基本稳定后，取相邻总阻力值的平均数，所得船模数值如表 3所示。这里模拟求得的船体总阻力值虽然包括了空气阻力，但由于空气阻力很小，故忽略不计，认为此所得值即为船体总阻力值。

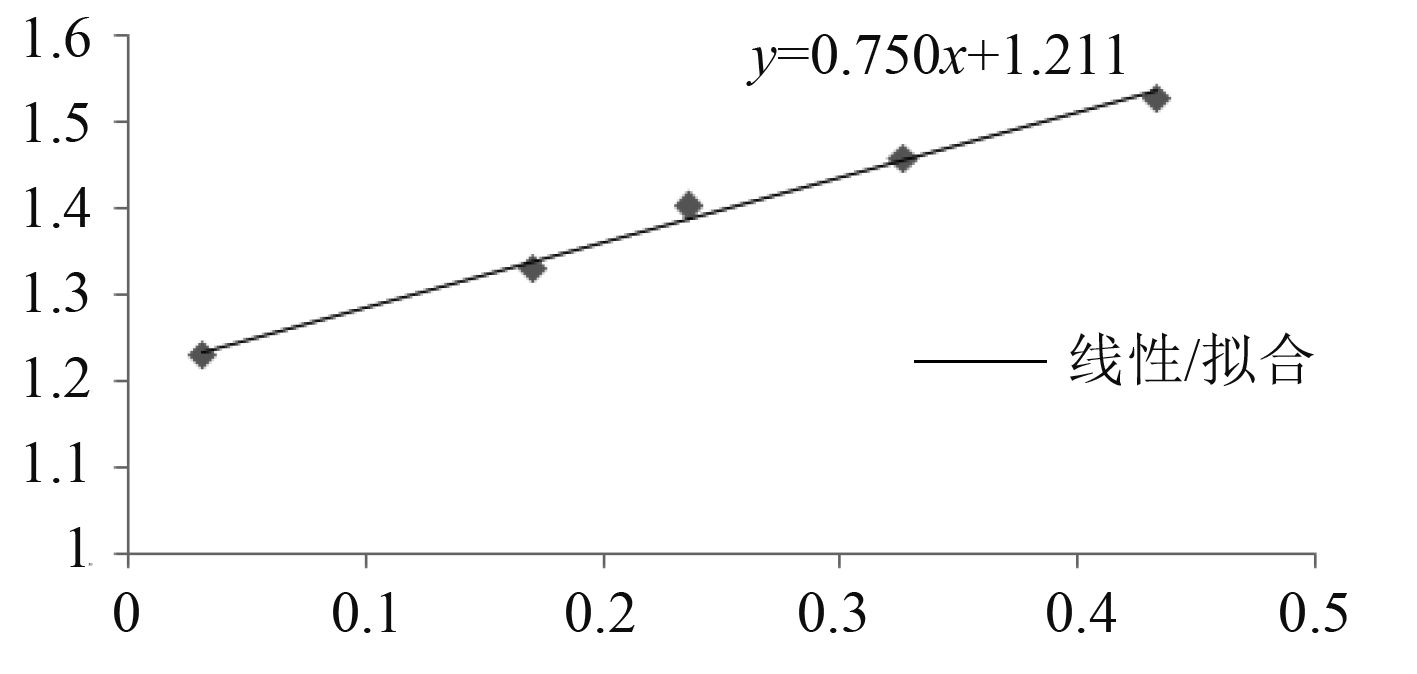
根据普鲁哈斯卡的假设，取傅汝德数在 0.1～0.2 之间的摩擦阻力系数和总阻力系数，将 $\frac{{{C_{tm}}}}{{{C_{fm}}}}$ 作为纵坐标 y， $\frac{{{F_r}^4}}{{{C_{fm}}}}$ 作为横坐标 x 作图，拟合出公式（见图 5），可得 1 + k = 1.211，即 k = 0.211。

根据式（5）和式（9）便可求得实船的总阻力系数和总阻力值。

此船的设计航速为 12 kn，傅汝德数为 0.160，属于低速船。对于低速船，粘性阻力所占比例往往较大，可达 70% 以上，兴波阻力所占比例较小，此船的数据正是符合这一规律，而且随着速度的增加，兴波阻力所占比例逐渐增大，总阻力值增长幅度也变大。

图 6为在航速 12 kn和 16 kn时的自由液面速度云图更直观地表现出了这一现象。当航速为 12 kn时，由于航速低，自由液面基本没有什么波动，速度分布较为平缓，船体周围有少量波动，兴波阻力很小；当模拟 16 kn航行时，船体周围的波动便相当显著，且不断向外扩散，兴波阻力明显变大。

可见，数值模拟比较真实的反映了船舶在海中航行时的状态。

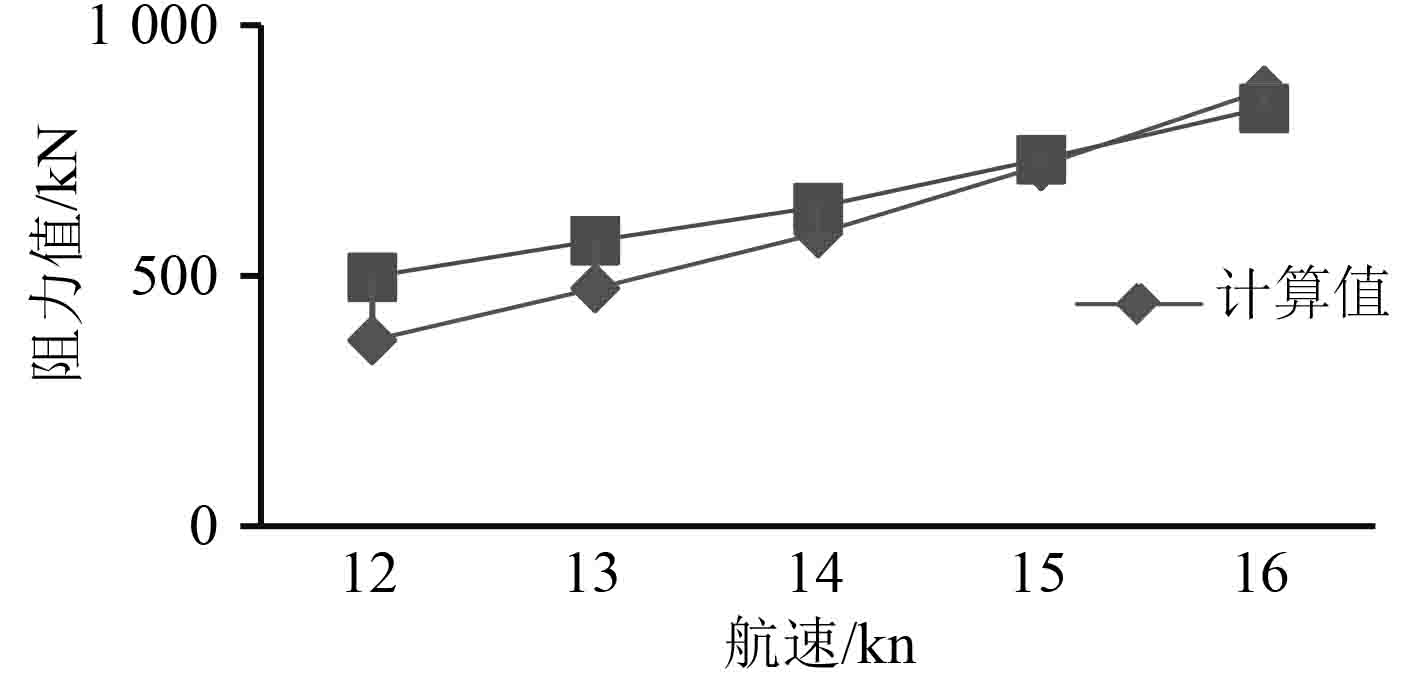
对该船采用艾亚法估算^[10]其阻力性能，并与模拟值进行比较（见表 5），同时绘出阻力随航速变化关系曲线（见图 7）。

由于航速为 6 kn和 8 kn的傅汝德数较低，超出了艾亚法估算查表的范围，所以只对比了 12 ~ 16 kn的阻力值。由以上图表可看出，在航速为 12 kn时，计算值与估算值的误差较大，随着航速的增加，误差逐渐缩小，且随着航速的增加，计算值上升的趋势大于估算值的趋势。这可能是对于肥大船修正系数不够引起的，而且该船拥有球鼻首，能在一定程度上降低阻力，艾亚法通常对于中低速船的估算结果较好，但由于艾亚法的统计资料属于上个世纪的船型，因而对于肥大型船的估计往往会产生一定误差，不过属于合理范围内。

4 结　语

本文采用数值模拟结合三因次法进行船舶阻力性能预报，通过计算结果发现CFD数值模拟确实能很好且相对快速的模拟船舶在不同航速下航行的状态，但前提是满足恰当的模型、高质量的网格和合理设置参数的要求。特别是网格数量和质量将直接影响到模拟的效果，而且湍流模型和求解方法的选取也会不同程度的影响模拟结果。实践证明RNG $k - \varepsilon $ 模型，SIMPLE算法和二阶迎风格式能有效的模拟，且网格设置外稀内密，且在100万左右基本能满足模拟要求。

根据普鲁哈斯卡假设和三因次方法，取傅汝德数在 0.1～0.2，利用最小二乘法拟合得到肥大型中低速船的形状系数为 0.211 相对准确。

本文只是在初步设计中对该多用途肥大船进行数值模拟研究，为多用途肥大船和船型优化提供一定借鉴，还需要进行船模试验进行更深入的研究。