由于海洋环境复杂,船舶、海洋平台、潜艇及潜水器等海洋结构物在服役期间通常承受各种各样的载荷作用,而疲劳损伤是结构破坏的主要形式之一。因此,对这些海洋结构物裂纹扩展速率和疲劳寿命进行准确预报具有很大的实际工程意义。试验研究结果表明,对于低周疲劳,结构的 70%~90% 寿命用在小裂纹阶段,而对于高周疲劳,结构的 95% 以上寿命用在小裂纹阶段。因此,基于断裂力学的方法将结构疲劳破坏看成一个连续破坏的过程,提出一个包含小裂纹扩展的疲劳寿命预报模型是具有工程应用价值的。这将为后续海洋结构物全寿命的研究奠定理论基础。
疲劳小裂纹问题首先是 1975 年Pearson发现的。他对铝合金长、小裂纹进行试验研究发现,在名义应力强度因子范围 ΔK 相同的条件下,长度为 0.006~0.5 mm的表面小裂纹的扩展速率比长度为几十毫米的长裂纹扩展快 100 倍,利用线弹性断裂力学方法很难将疲劳小裂纹扩展速率与长裂纹扩展速率相联系[1]。并且小裂纹在低于长裂纹门槛值下仍能扩展。在Pearson之后,许多学者对疲劳小裂纹扩展进行了研究,并在断裂力学基础上进行了疲劳寿命的预报。研究发现,许多材料疲劳小裂纹扩展行为具有一个共同的特点,在相同应力强度因子范围下,小裂纹扩展速率要明显高于长裂纹扩展速率;即使在长裂纹的应力强度因子门槛值以下小裂纹还能够扩展;如果用基于长裂纹扩展的试验数据来预报小裂纹疲劳寿命,显然不精确。
本文在王珂[2]提出的考虑小裂纹效应的疲劳寿命预报修正模型的基础上对裂纹尖端塑性区域修正因子进行了重新修正。修正后的模型能够预报裂纹尺寸小于材料微结构的小裂纹的扩展行为,模型包括了疲劳裂纹扩展典型的 3 个阶段。通过对钛合金TC4 的小裂纹扩展行为的预报,发现在高应力水平时修正后模型对疲劳寿命的预报更为准确,能很好地解释材料的疲劳小裂纹效应。
1 小裂纹扩展速率模型 1.1 考虑小裂纹效应修正模型小裂纹的扩展寿命在疲劳总寿命中占到了很大的比例,其扩展行为与长裂纹扩展行为相比有着很大的差别。小裂纹的扩展行为具有以下 3 大特点[3]:
1)疲劳小裂纹的尖端塑性区域尺寸和小裂纹长度相比不可忽略,因而疲劳小裂纹的扩展行为是一个弹塑性非线性问题而不是和长裂纹扩展一样被认为是一个线性问题;
2)疲劳小裂纹其裂纹闭合水平是裂纹长度的函数。当小裂纹为微观小裂纹时,裂纹闭合水平近似为 0;当裂纹不断扩展时,裂纹闭合水平逐渐扩展的长裂纹闭合的饱和水平;
3)小裂纹具有Kitagawa效应。对于小裂纹而言,控制疲劳小裂纹扩展行为的是材料的疲劳极限,而不是控制长裂纹的疲劳裂纹门槛值,即疲劳小裂纹时疲劳循环应力控制裂纹扩展,宏观疲劳长裂纹时应力强度因子范围控制裂纹扩展。
基于疲劳小裂纹扩展的 3 大特点,王珂在疲劳寿命预报统一方法(Cui,2011)和Chapetti模型(2003)的基础上,提出了考虑小裂纹效应的修正模型。该模型考虑了裂纹尖端塑性区域平面应力状态下的修正以及小裂纹门槛值与裂纹长度的关系。不仅适用于小裂纹扩展行为的预报,也适用于疲劳裂纹扩展的其他典型阶段,成功地解释了疲劳试验中许多金属疲劳的现象。其修正后模型如下:
| $ \frac{{{\rm d}a}}{{{\rm d}N}} \!\!=\!\! A \! \frac{{{{[\Delta K \!-\! (\Delta {K_{th \!-\! R}} \!-\! \Delta {K_{th \!-\! s}})(1 \!-\! {e^{ - k(a - d)}}) \!-\! \Delta {K_{th - s}}]}^m}}}{{1 - {{({K_{\max }} - {K_C})}^n}}}, \!\! $ | (1) |
| $\Delta K = (1 - R){K_{\max }} = {K_{\max }} - {K_{\min }},$ | (2) |
| ${K_{\max }} = Y{\sigma _{\max }}\sqrt {\pi aF}, $ | (3) |
| $d = \frac{1}{\pi }{(\frac{{\Delta {K_{th - s}}}}{{Y{\sigma _R}}})^2},$ | (4) |
式中:
A 为材料环境常数,MPa
– mm
1-m/2;
Y 为几何修正因子;
a 为裂纹长度,m;
n 为
K
max/
K
min 影响能力参数;
m 为裂纹扩展速率曲线斜率;
R 为疲劳循环载荷中的应力比;
K
max 为最大应力强度因子,MPam
1/2;
K
min 为最小应力强度因子,MPam
1/2;
F 为裂纹尖端塑性区域修正因子;
d 为材料内部裂纹长度;
ΔK
th-R
为载荷比为
R 时长裂纹扩展门槛值,MPam
1/2;
在该修正公式中 F 为裂纹尖端处于平面应力作用下的裂纹尖端塑性区域修正因子,其表达式为:
| $F = \frac{1}{2}(\sec \frac{{{\sigma _{\max }}}}{{{\sigma _{fl}}}} + 1) \text{。}$ | (5) |
式中: σ fl 为材料的流变应力,其值等于材料的屈服强度与极限强度和的一半; σ max 为交变载荷中的最大应力,MPa。
1.2 疲劳小裂纹尖端塑性区域尺寸的修正金属材料在疲劳小裂纹阶段,裂纹尖端塑性区域的尺寸与小裂纹本身的长度相近,不可忽略。所以,小裂纹扩展行为是弹塑性非线性的而不是线弹性的。根据Irwin1960 年提出的修正理论[4]:疲劳小裂纹的裂纹长度等于实际裂纹的长度加上裂纹尖端塑性区域尺寸的一半。由此,修正后裂纹的长度为:
| ${a_{od }} = a + \frac{1}{2}{r_\varepsilon }{\rm{ = }}aF,$ | (6) |
式中: a mod 为修正后裂纹长度; a 为实际裂纹长度; r ε 裂纹尖端塑性区域尺寸,m; F 为裂纹长度修正因子。
研究表明当板材较薄时是其疲劳断裂截面可近似为平面,此时可将应力问题看作为平面应力问题。但是随着板材厚度的逐渐增加,结构也逐渐表现为平面应变问题。所以本文将裂纹尖端区域的问题看成平面应变问题而不是看成平面应力问题。
由Hooke定律和Irwin(1960)提出的理论,裂纹尖端塑性区域的尺寸为:
| ${r_\varepsilon } = \frac{1}{{6\pi }}{(\frac{K}{{{\sigma _Y}}})^2} \text{,} $ | (7) |
式中: r ε 为裂纹尖端塑性区域尺寸,m; K 为应力强度因子,MPam 1/2; σ Y 为材料的屈服应力,MPa。
因此根据Dugdale(1960)提出的理论可知[5]:
| $\frac{1}{{2\pi }}{(\frac{K}{{{{\rm{\sigma }}_Y}}})^2} = \frac{a}{2}({\rm sec}\frac{{{\pi _{\max }}}}{{2{{\rm{\sigma }}_Y}}} - 1)\text{,}$ | (8) |
式中: σ max 为循环载荷中的最大应力,MPa; a 为裂纹长度,m; σ Y 为材料的屈服强度。
将应力强度因子 K 带入并用材料的流变应力 σ fl 来代替材料的屈服应力 σ Y ,则有:
| ${a_{od }} = a + \frac{a}{{12}}(\sec \frac{{\pi {\sigma _{\max }}}}{{{\sigma _{fl}}}} - 1)\text{,}$ | (9) |
故有:
| ${F^,} = \frac{1}{{12}}(\sec \frac{{{\sigma _{\max }}}}{{{\sigma _{fl}}}} + 11) \text{。} $ | (10) |
式中 σ fl 为材料的流变应力,其值等于材料的屈服强度 σ y 与极限强度 σ μ 和的一半。
2 钛合金疲劳小裂纹扩展行为预报目前,钛合金材料被广泛应用于船舶、航空等领域。Peter等对钛合金材料Ti-6Al-4V在不中状况下的小裂纹疲劳断裂行为进行了实验研究。本文依据上述试验资料选取几种典型状况利用疲劳小裂纹统一预报修正模型对钛合金Ti-6Al-4V和 α + β 热处理钛合金进行了小裂纹扩展速率与寿命的预报,并将预报结与对应试验结果进行比较,以此来验证该修正模型的准确性[6]。
由文献资料钛合金Ti-6Al-4V当载荷比 R = – 1 时长裂纹门槛值 ΔK th-R 为 5.6 MPam 1/2;当载荷比 R = 0.1 时长裂纹门槛值 ΔK th-R 为 4.8 MPam 1/2。预报时假设试件中的裂纹为半圆形表面裂纹,其具体材料参数及预报模型参数如表 1所示。
|
|
表 1 钛合金材料参数表 Tab.1 Summary of the material properties |
通过预报模型对 2 种钛合金材料的小裂纹扩展速率进行预报并与试验数据进行对比其结果如图 1~ 图 6所示
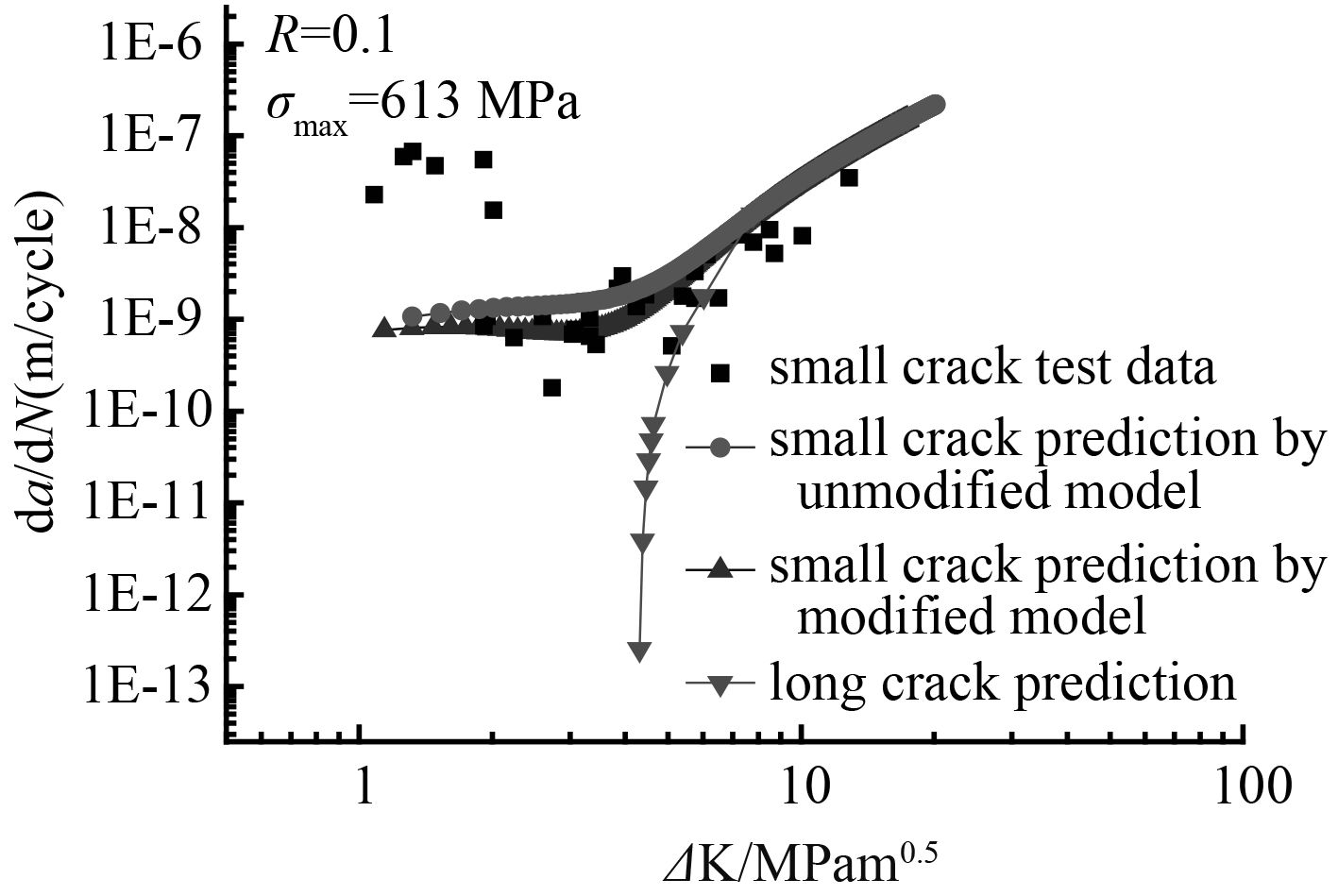
|
图 1 钛合金Ti-6Al-4V小裂纹扩展预报值与实验结果对比( σ max = 613 MPa) Fig. 1 Comparison of experimental and predicted crack growth rates for titanium alloy Ti-6Al-4V ( σ max = 613 MPa) |
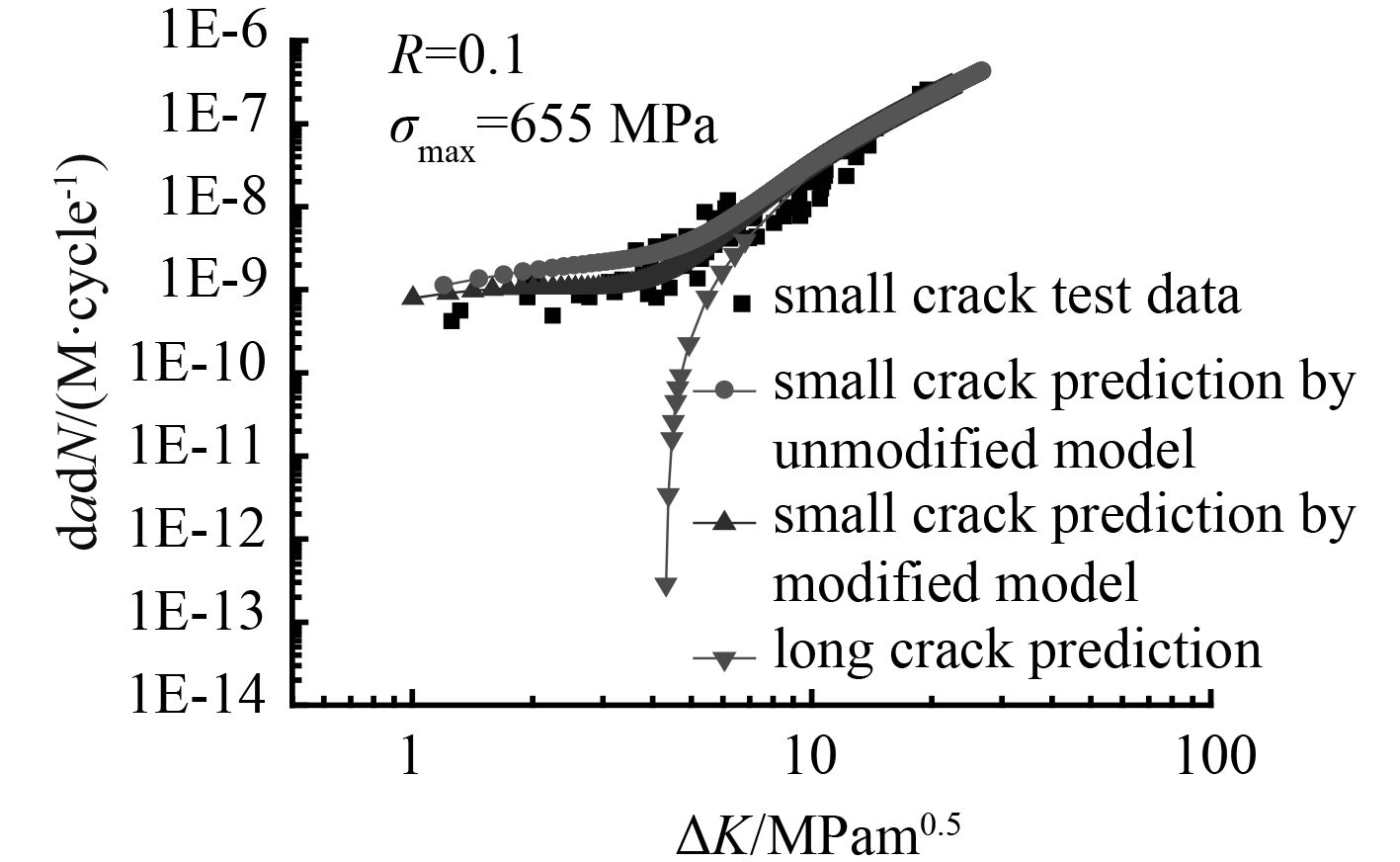
|
图 2 钛合金Ti-6Al-4V小裂纹扩展预报值与实验结果对比( σ max = 655 MPa) Fig. 2 Comparison of experimental and predicted crack growth rates for titanium alloy Ti-6Al-4V ( σ max = 655 MPa) |
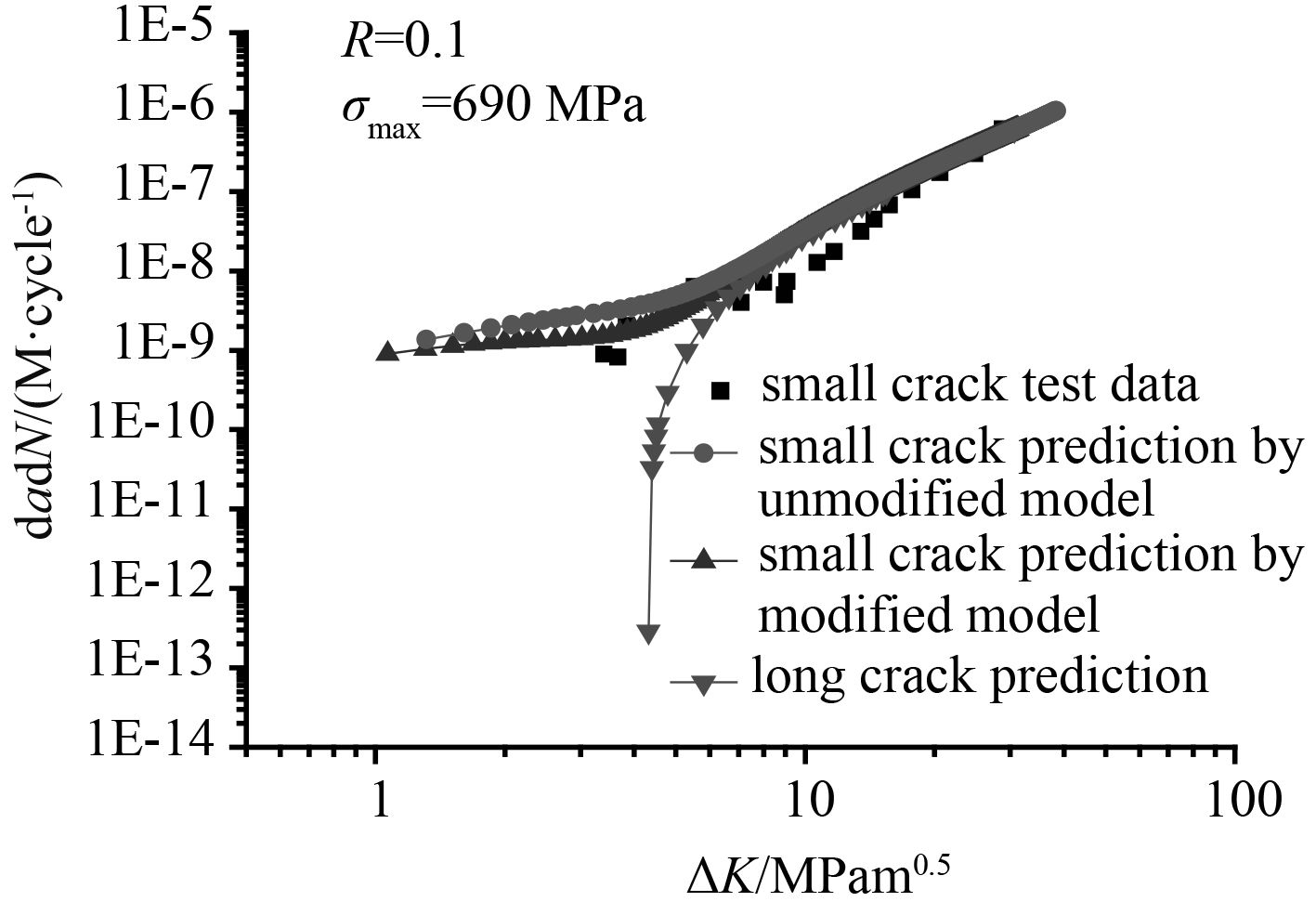
|
图 3 钛合金ti-6Al-4V小裂纹扩展预报值与试验结果对比( σ max = 690 MPa) Fig. 3 Comparison of experimental and predicted crack growth rates for titanium alloy Ti-6Al-4V ( σ max = 690 MPa) |
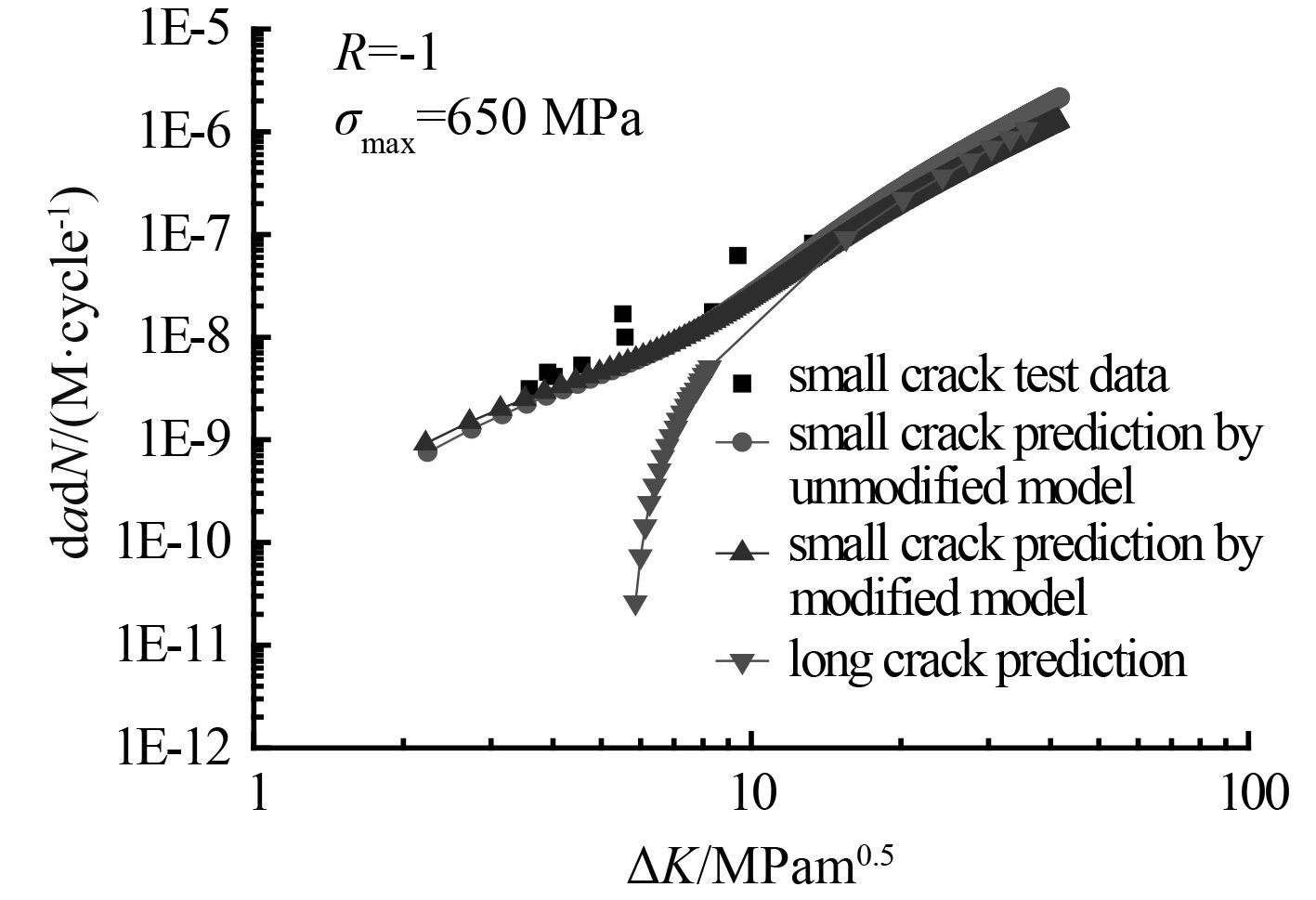
|
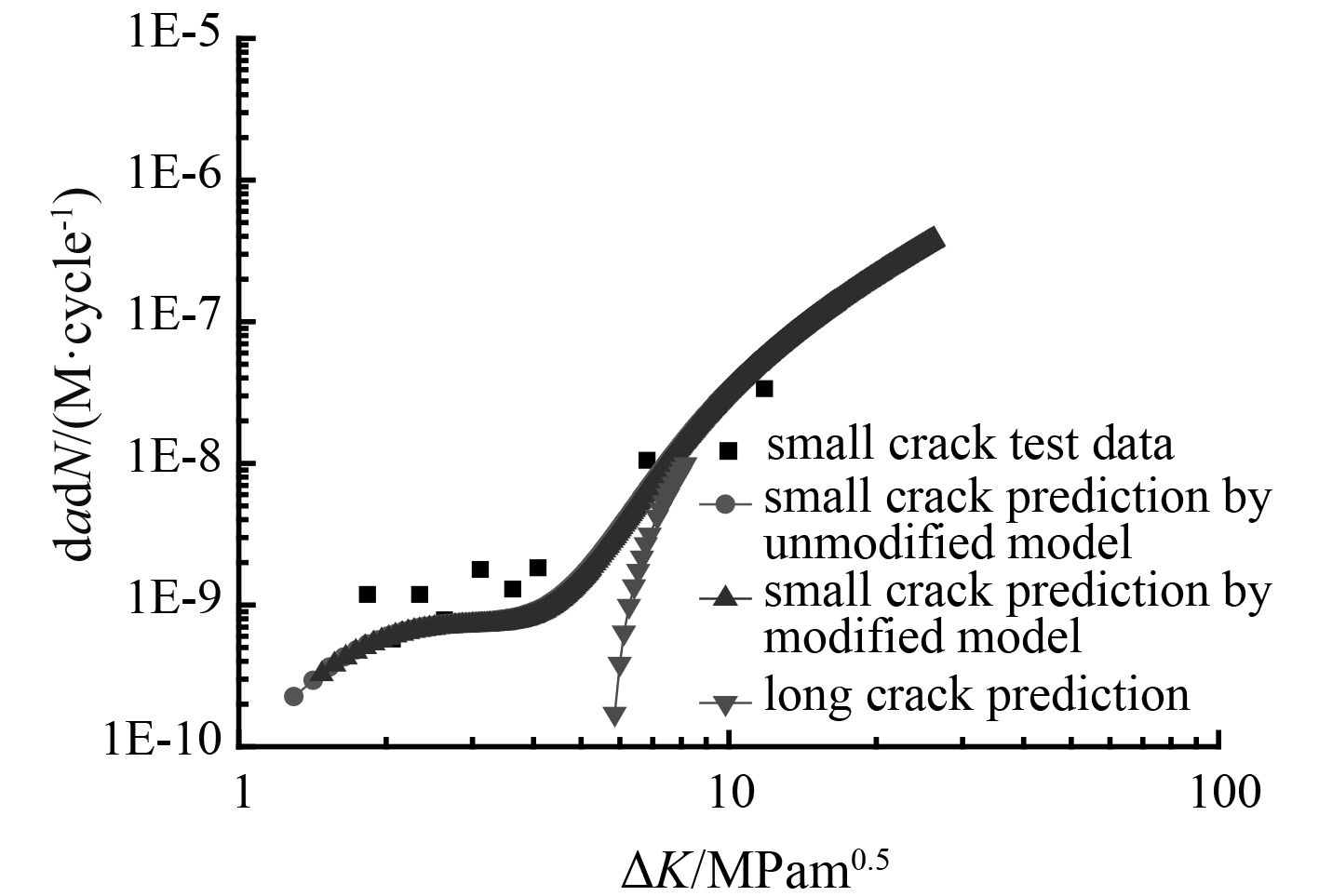
图 4 钛合金小裂纹扩展预报值与试验结果对比图 Fig. 4 Comparison of experimental and predicted crack growth rates for titanium alloy Ti-6Al-4V |
|
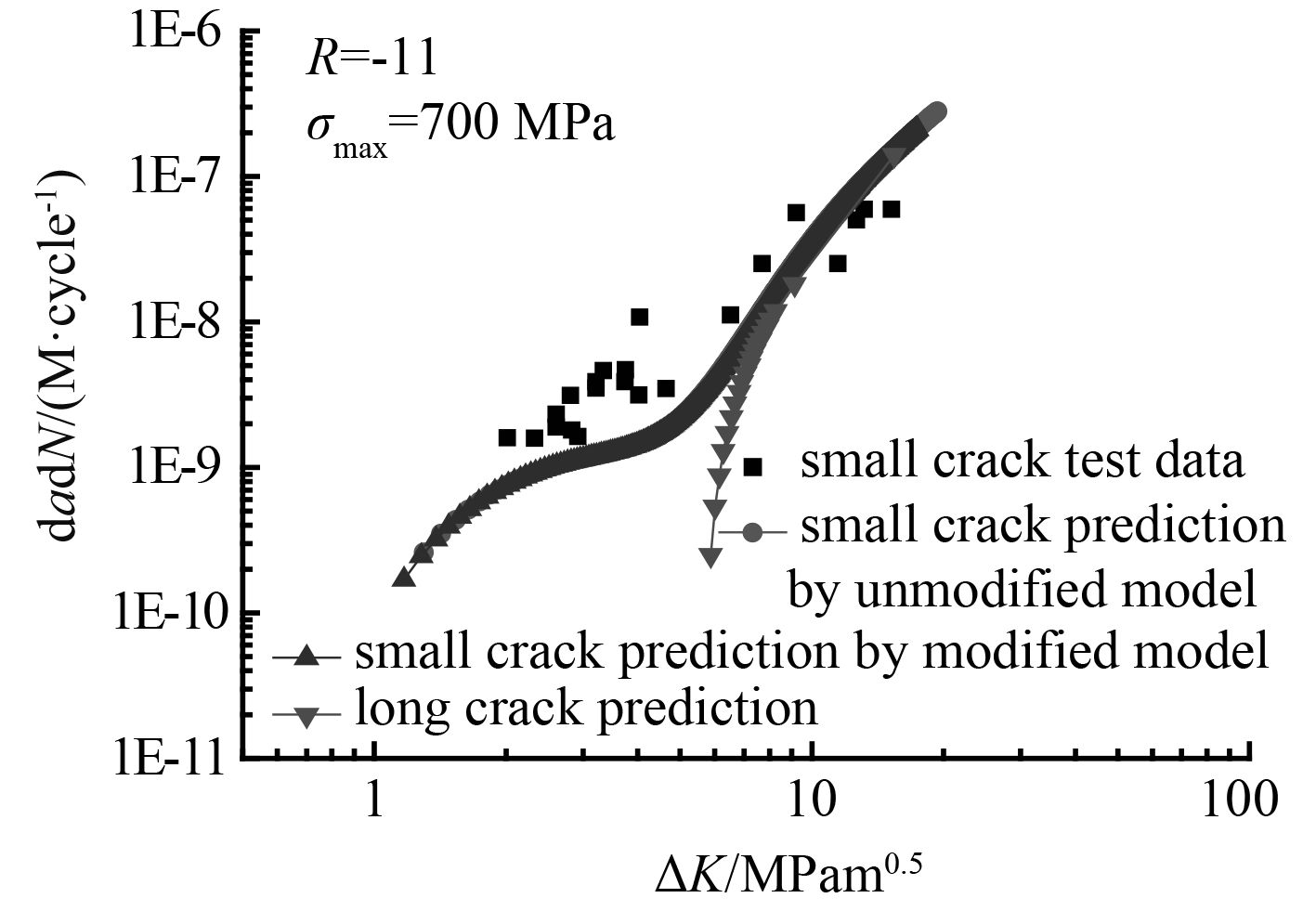
图 5 α + β 钛合金小裂纹扩展预报值与试验结果对比图 Fig. 5 Comparison of experimental and predicted crack growth rates for titanium (α + β processed) |
|
图 6 钛合金( β 处理)小裂纹扩展速率预报值与试验结果对比 Fig. 6 Comparison of experimental and predicted crack growth rates for titanium alloy ( β processed) |
由图可看出,修正模型对钛合金疲劳小裂纹的预报值和试验值有很好的吻合。 图 1~ 图 3反映了在载荷比 R 一定时最大应力水平对钛合金疲劳小裂纹扩展速率的影响。从图中可看出,修正后的模型与试验值吻合跟好。当应力强度因子较小时平面应变状态下裂纹扩展速率的预报值要小于平面应力状态下裂纹扩展速率的预报值。并且当应力强度因子范围小于长裂纹门槛值 4.8 MPam 1/2 时小裂纹仍可以继续扩展。同时可以看出当应力强度因子小于 10 MPam 1/2(即裂纹长度小于 0.2 mm)时,在相同应力强度因子范围下小裂纹扩展速率大于长裂纹预报值。随着裂纹长度的增加各曲线均与长裂纹扩展速率重合。 图 4~ 图 6反映了不同微结构的钛合金Ti-6Al-4V在不同加载状态下的小裂纹扩展特点。裂纹扩展速率与应力强度因子范围总体呈正相关关系;当应力强度因子范围小于长裂纹门槛值 ΔK th-R = 5.6 MPam 1/2 时小裂纹仍继续扩展,并且在相同的应力强度因子范围下钛合金小裂纹扩展速率均高于长裂纹的裂纹扩展速率;随着小裂纹尺寸的不断增加,应力强度因子范围逐渐增大,钛合金的疲劳小裂纹扩展速率逐渐与长裂纹扩展速率重合。图中修正后的裂纹扩展速率曲线与原先的疲劳裂纹扩展速率曲线近乎重合,这表明在小裂纹阶段,尖端塑性区域看成何种状态对裂纹扩展速率的影响不大。从预报曲线与试验数据的对比可以看出在整个应力强度因子范围内修正模型对 2 种钛合金的裂纹扩展速率都具有较强的预报能力,很好地反映了钛合金材料的小裂纹扩展特点。
利用本文模型对 2 种钛合金材料的疲劳寿命进行预报研究并将预报结果与试验值(Peter,2001)及未修正模型的预报值进行对比,其结果如图 7~ 图 9所示。
|
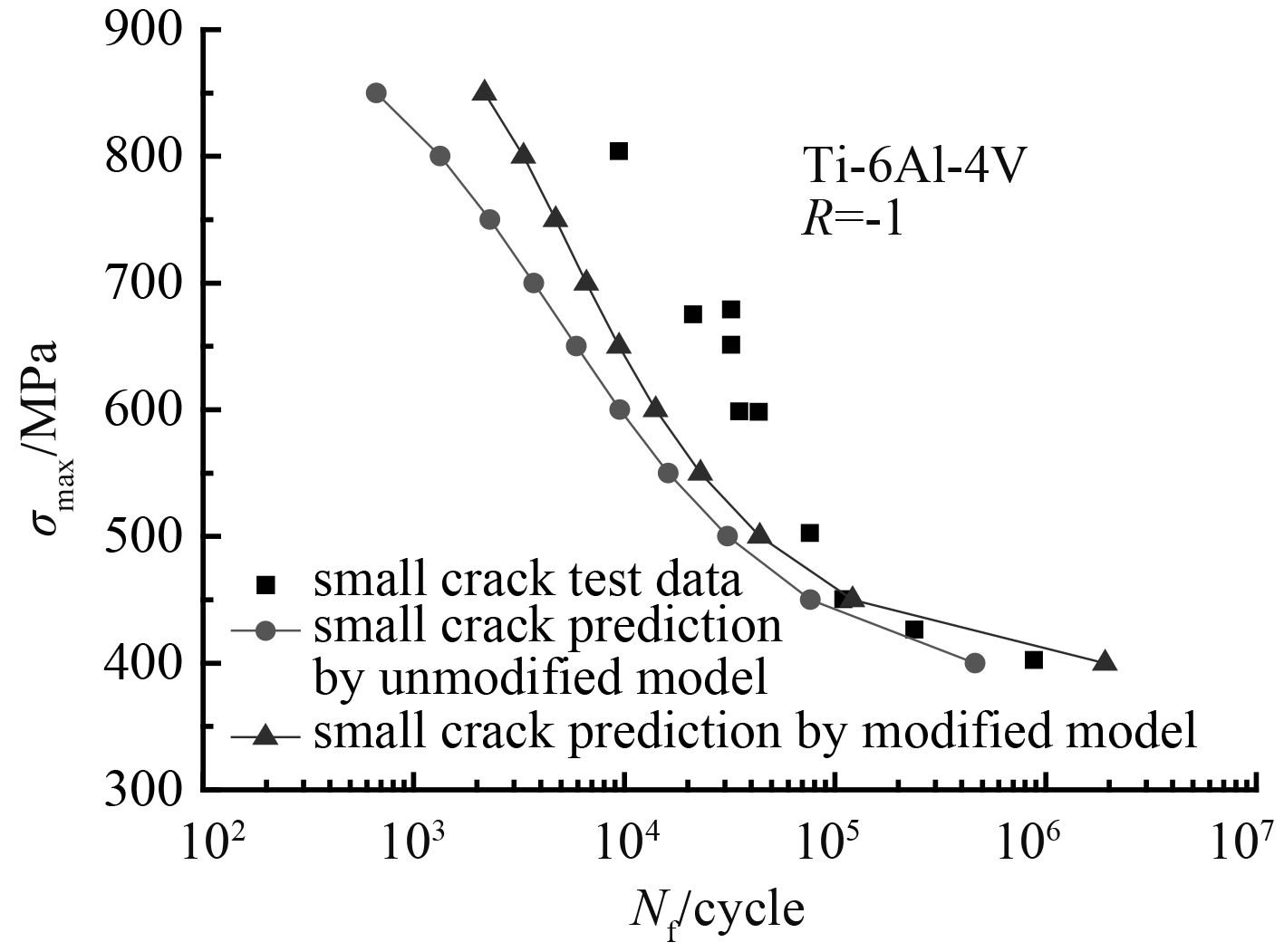
图 7 钛合金Ti-6Al-4V疲劳寿命预报值对比( R = –1) Fig. 7 Comparison of experimental and predicted fatigue lives for titanium alloys |
|
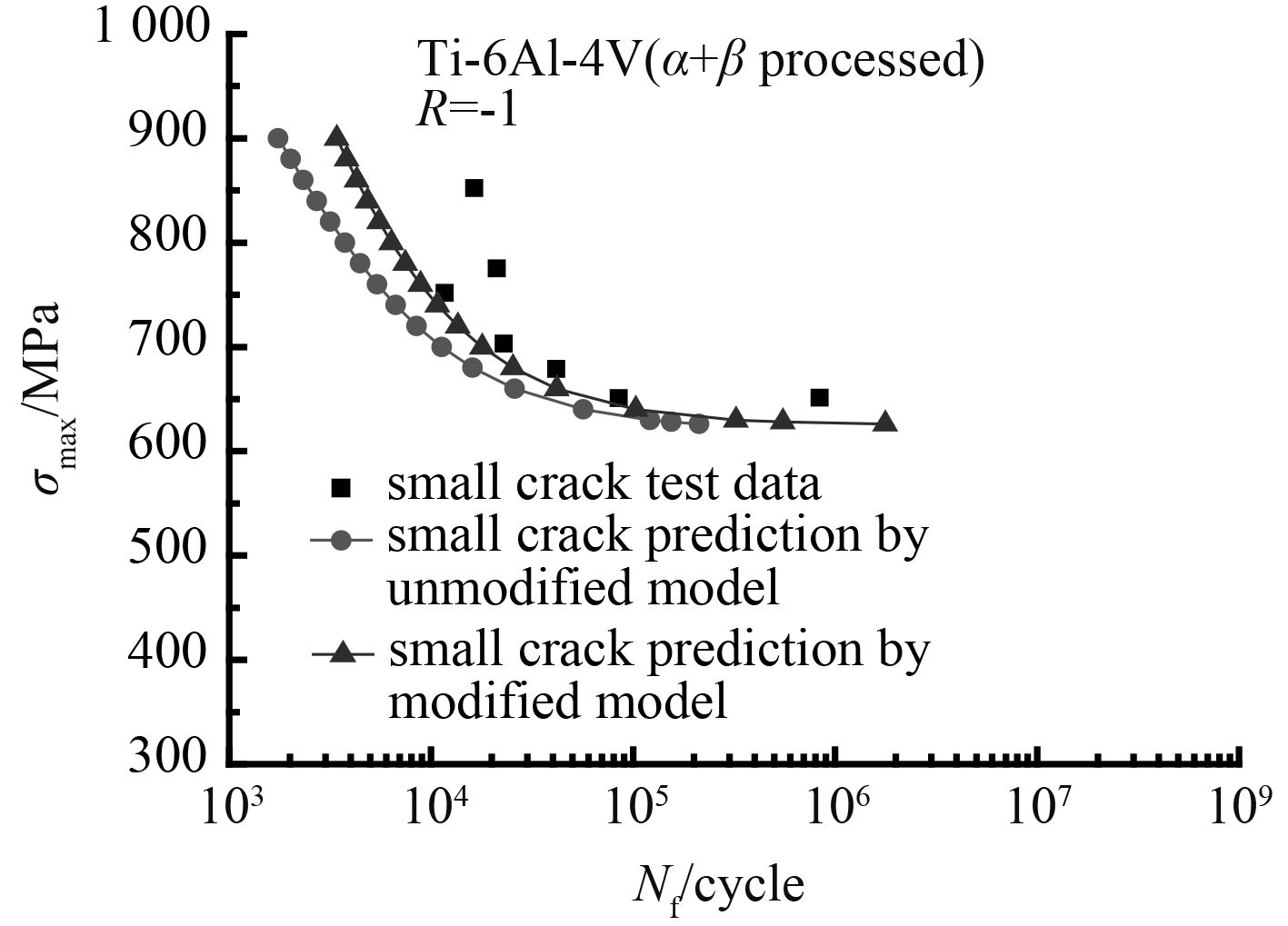
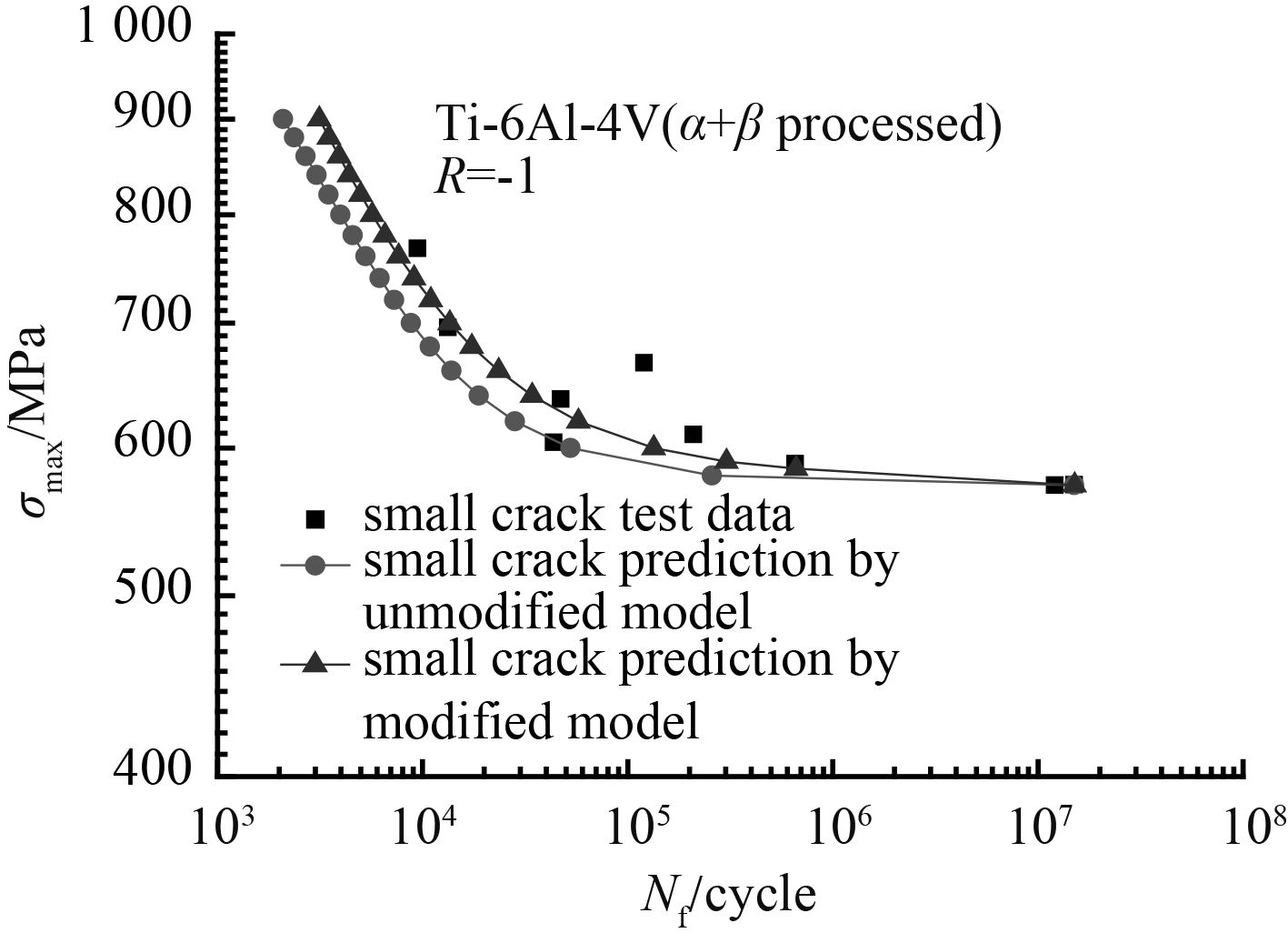
图 8 α + β 热处理钛合金疲劳寿命预报值对比 Fig. 8 Comparison of experimental and predicted fatigue lives for titanium alloys( α + β processed) |
|
图 9 β 热处理钛合金疲劳寿命预报值对比 Fig. 9 Comparison of experimental and predicted fatigue lives for titanium alloys( β processed) |
由图可以看出:修正后的模型与原来模型相比,修正后的模型对钛合金的寿命预报更为准确,尤其是在应力水平较高时。从图可以看出在最大应力高于材料屈服应力时,修正模型的预报值与试验值相比略小于试验值。这是由于当应力水平较高时,材料在试验过程中产生了应变硬化,即材料在经历了屈服阶段以后增加了其抵抗变形的能力,但从曲线的整体的趋势看修正模型对 2 种钛合金材料的寿命有很好的预报能力。
3 结 语本文提出在疲劳裂纹扩展统一预报模型的基础上,考虑小裂纹效应,针对裂纹尖端塑性区域的应力状态,提出了疲劳裂纹扩展统一预报修正模型并通过预报研究得出以下结论。
1)预报模型对钛合金的疲劳裂纹扩展行为具有很强的预报能力。
2)将小裂纹尖端塑性区域考虑成平面应变状态当应力强度因子范围较小时其对裂纹扩展速率略有影响,随着裂纹长度的不断增加,逐渐与长裂纹预报值重合。
3)修正后模型对 2 种钛合金材料寿命的预报值更为准确,但当应力水平较高时由于材料应变硬化的缘故,预报结果还存在一定的误差。
4)材料的微结构直接影响钛合金的疲劳裂纹扩展行为,热处理增强了材料的抗疲劳性能。
| [1] | PEARSON S. Initiation of fatigue cracks in commercial aluminium alloys and the subsequent propagation of very short cracks[J]. Engineering Fracture Mechanics, 1975, 7 (2): 235–247. DOI: 10.1016/0013-7944(75)90004-1 |
| [2] | WANG K, WANG F, CUI W, et al. Prediction of short fatigue crack growth of Ti-6Al-4V[J]. Fatigue & Fracture of Engineering Materials & Structures, 2014, 37 (10): 1075–1086. |
| [3] | MCEVILY A J. An analysis of the growth of small fatigue cracks[J]. Materials Science and Engineering: A, 1991, 143 (1): 127–133. |
| [4] | IREIN G R. Fracture Mode transition for a crack traversing a plate[J]. Journal of Fluids Engineering, 1960, 82 (2). |
| [5] | DUGDALE D S. Yielding of steel sheets containing slits[J]. Journal of the Mechanics & Physics of Solids, 1960, 8 (2): 100–104. |
| [6] | PETERS J O, LÜTJERING G. Comparison of the fatigue and fracture of α+β and β titanium alloys[J]. Metallurgical & Materials Transactions A, 2001, 32(11): 2805–2818(14). https://link.springer.com/article/10.1007/s11661-001-1031-8 |
 2017, Vol. 39
2017, Vol. 39
