0 引　言

加筋板被广泛应用于许多工程结构中，它大大提高了板的承载能力。在加筋板的设计中，加筋板的稳定性是一个必须考虑的重要因素，同时由于加筋板稳定性问题的复杂性，对加筋板稳定性的研究显得尤为重要^[1]。加筋板结构为船体甲板结构的基本构件，其稳定性直接影响整体结构的承载能力。舰船在中垂状态时甲板板架受总纵弯曲轴向压力，甲板板架是距离中和轴最远的主船体受压结构，所受的轴向压力最大，只有保证甲板的稳定性，才能保证舰船整体结构的稳定性^[2]。加筋板作为船体甲板的主要结构单元，研究其稳定性十分必要。船用加筋板结构屈曲行为一般分为板的屈曲、加强筋屈曲、加强筋之间的板格屈曲和加筋板格的整体屈曲 4 种^{[3 –4]}。其中加筋板的整体屈曲是最危险的屈曲情况。

加筋板结构在长期使用过程中，由于各种载荷的作用，会产生固定的初始挠度变形。初始挠度变形对加筋板的稳定性和极限承载能力都会产生严重不利影响。因此，在加筋板的稳定性分析中，考虑初始变形等因素的影响，具有重要的工程意义。

目前，国内考虑初始挠度变形对结构稳定性影响的研究较多。但研究初始挠度的具体形式对加筋板稳定性影响较少；而且对船用加筋板初始挠度的考虑都是基于船体结构建造时的测量的数据，并未考虑舰船长期服役之后产生的挠度变形的具体情况以及其对加筋板稳定性产生的影响。本文主要考虑舰船长期服役之后，加筋板的整体挠度变形情况对其稳定性的影响。假设初始挠度为双级数形式，利用有限元方法计算含初始挠度加筋板的弹性失稳压力。并通过控制初始挠度函数形式，讨论初始挠度的幅值与半波数对弹性失稳压力的影响，最后得到初始挠度对加筋板稳定性的影响因子。

1 含初始挠度加筋板的稳定性分析 1.1 有限元模型建立

本文根据某舰船的甲板结构，选取甲板典型位置处的某一加筋板作为研究对象。该加筋板具有 6 条纵向加强筋，板尺寸 a × b 为 1 500 mm × 2 800 mm，加强筋间距 s = 400 mm，加强筋均为角钢，角钢尺寸为「 $\frac{{6 \times 100}}{{6 \times 26}}$ 。

研究中，利用有限元分析软件Ansys，根据加筋板的具体尺寸，建立合适的有限元模型。采用shell181 单元，单元长度在 20～30 mm之间，计算中假定板的材料是理想弹塑性，弹性模量 E = 2.1 × 10 ⁵ MPa，泊松比 ν = 0.3。

加筋板的边界条件定义为四边简支，具体定义方法可以参照相关文献^[5]：

1）加筋板的四周边界限制法向位移 U _z = 0，即为 z 方向简支；

2）长度方向两端 AB， CD 边（ x = 0 和 x = a 处）限制转角位移 R _x = R _z = 0，即可沿 y 方向自由转动；宽度方向两端 AD， BC 边（ y = 0 和 y = b 处）限制转角位移 R _y = R _z = 0，即可沿 x 方向自由转动；

3） AB， CD 边线保持沿 x 方向的直边约束， AD， BC 边线保持沿 y 方向的直边约束；

4） AB、 CD 边线中点限制 y 方向位移，即 U _y = 0， AD、 BC边线中点限制 x 方向位移，即 U _x = 0。

加筋板的外载荷施加方式为在 AB， CD 两端截面同时施加轴向压力为 1 MPa的集中力载荷，在有限元软件中转换施加到截面节点上。有限元模型的边界条件和载荷施加情况如图 1所示。

1.2 初始挠度设计

初始挠度这种结构上的缺陷可分为整体和局部 2 种形态。整体初始挠度是指板和加强筋同时产生挠度变形；局部初始挠度是指仅板产生的挠度变形。初始挠度形态主要包括两方面因素，即幅值和半波数。在较长的跨度范围内，初始挠度是由多个半波所组成的曲面，而在较短的范围内（ 2 个加强筋之间）一般只有一个半波。船体加筋板初始挠度形态可以看成由多种半波形式叠加而成，可用如下公式表示：

$w = \sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{A_{mn}}\sin \frac{{m\pi x}}{a}\sin \frac{{n\pi y}}{b}} }\text{，} $

(1)

也有用如下公式来表示焊接作用导致加筋板产生的挠度变形^[6]：

$\frac{{{w_0}}}{{{w_{opl}}}} = {B_{oi}}\sin \frac{{i\pi x}}{a}\sin \frac{{\pi y}}{b}\text{，} $

(2)

式中： ${w_0}$ 为初始挠度，mm； ${w_{opl}}$ 为加强筋间板格的最大初始挠度，mm； ${B_{oi}}$ 为初始变形幅值，mm。

加筋板结构的一阶屈曲模态是最容易产生的失稳状态，对加筋板的稳定性有重要影响^[7]。一般认为，取一阶模态作为结构的初始缺陷比较合理。本文在考虑初始挠度时，并不是考虑焊接影响产生的挠度变形，而是考虑长期外载荷作用下产生的挠度变形，这种挠度变形在加载之前就已经存在，故称为初始挠度。根据舰船甲板实际情况，可以假设初始挠度用下式表示：

$w = A\sin \frac{{i\pi x}}{a}\sin \frac{{\pi y}}{b}\text{。}$

(3)

考虑半波数对弹性失稳压力的影响时，限定 y 方向为一个半波，只考虑 x 方向半波数的影响。

本文拟采用式（3）的初始挠度形式模拟实际初始挠度情况，来研究整体初始挠度的幅值和半波数对加筋板弹性失稳压力的影响。

根据船厂生产实践和调研结果，当强力甲板厚度在 7～10 mm之间时，钢板的绝对变形量达到 35 mm时，才会对钢板进行矫正修复；从对我国甲板变形测量的数据统计来看，甲板变形一般在 8 mm左右。为了使研究更具有实用性，本文将初始挠度幅值设定在 0～30 mm之间进行计算研究。国内关于舰船甲板板架变形的半波数测量研究内容较少。国外有对船厂建造中船体变形情况测量的研究^[8]，初始挠度的半波数一般在 3 个以内。本文根据施加初始挠度的实际情况，决定最多取 6 个半波作为研究对象。

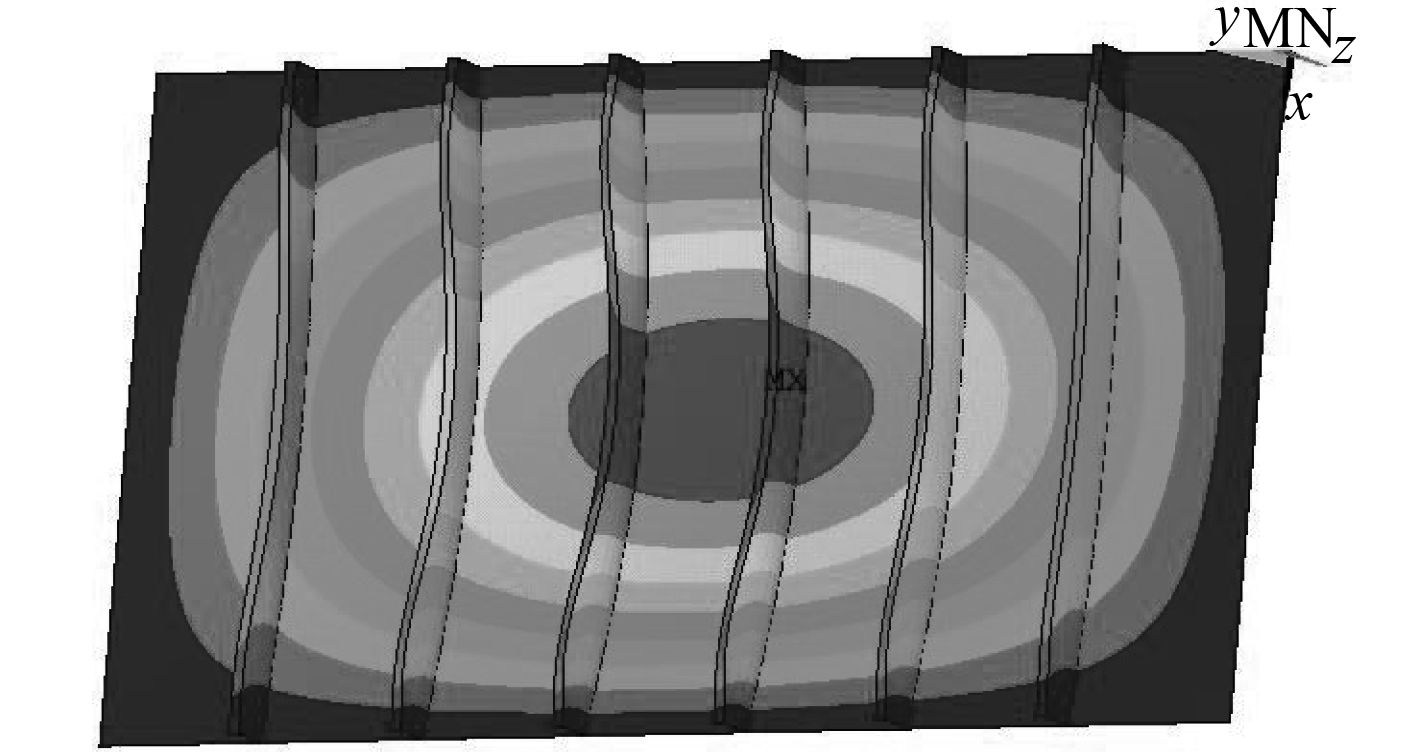
1.3 初始挠度对弹性失稳压力的影响

在有限元软件Ansys中，可以通过对各个节点施加具体的法向位移来实现初始挠度的设计与施加。 图 2所示为具有 1 mm幅值、一个半波初始挠度的加筋板。

当计算模型不具有初始挠度时，计算所得弹性失稳压力为 333.012 MPa。通过不断改变初始挠度的幅值和半波数，计算相应的弹性失稳压力数值，计算数据见表 1。

1.3.1 初始挠度幅值对加筋板弹性失稳压力的影响

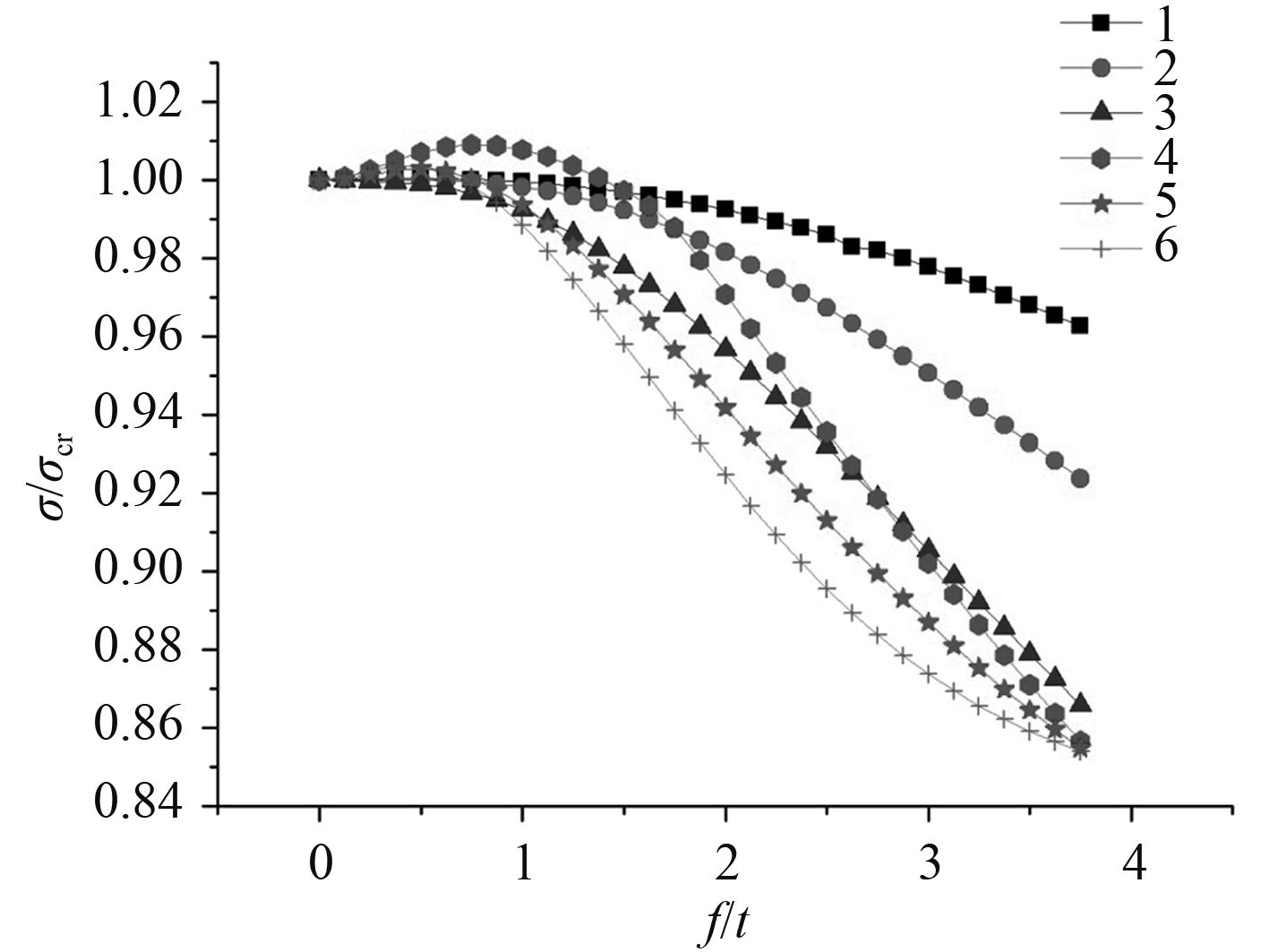
根据计算数据可以绘制出弹性失稳压力与初始挠度幅值的关系图，从而可以判定，在某一半波数情况下，弹性失稳压力随初始挠度幅值的变化规律。为了更加方便比较不同半波数的初始挠度情况下，弹性失稳压力随幅值的变化规律，将各个半波数下的曲线绘制到同一个坐标系下，并考虑将初始挠度幅值和弹性失稳压力转化为无因次量，取初始挠度幅值 f 与加筋板厚度 t 的比值为自变量，取含初始挠度加筋板弹性失稳压力 σ 与不含初始挠度加筋板弹性失稳压力 σ _cr 比值作为因变量，如图 3所示。

从图中可看出，曲线整体呈现半波数越大，弹性失稳压力的变化率越大的规律。在幅值较小的一定范围内，含初始挠度加筋板弹性失稳压力大于不含初始挠度加筋板的弹性失稳压力，该范围即可以称为有利范围；超过一定范围，弹性失稳压力小于原来的弹性失稳压力。

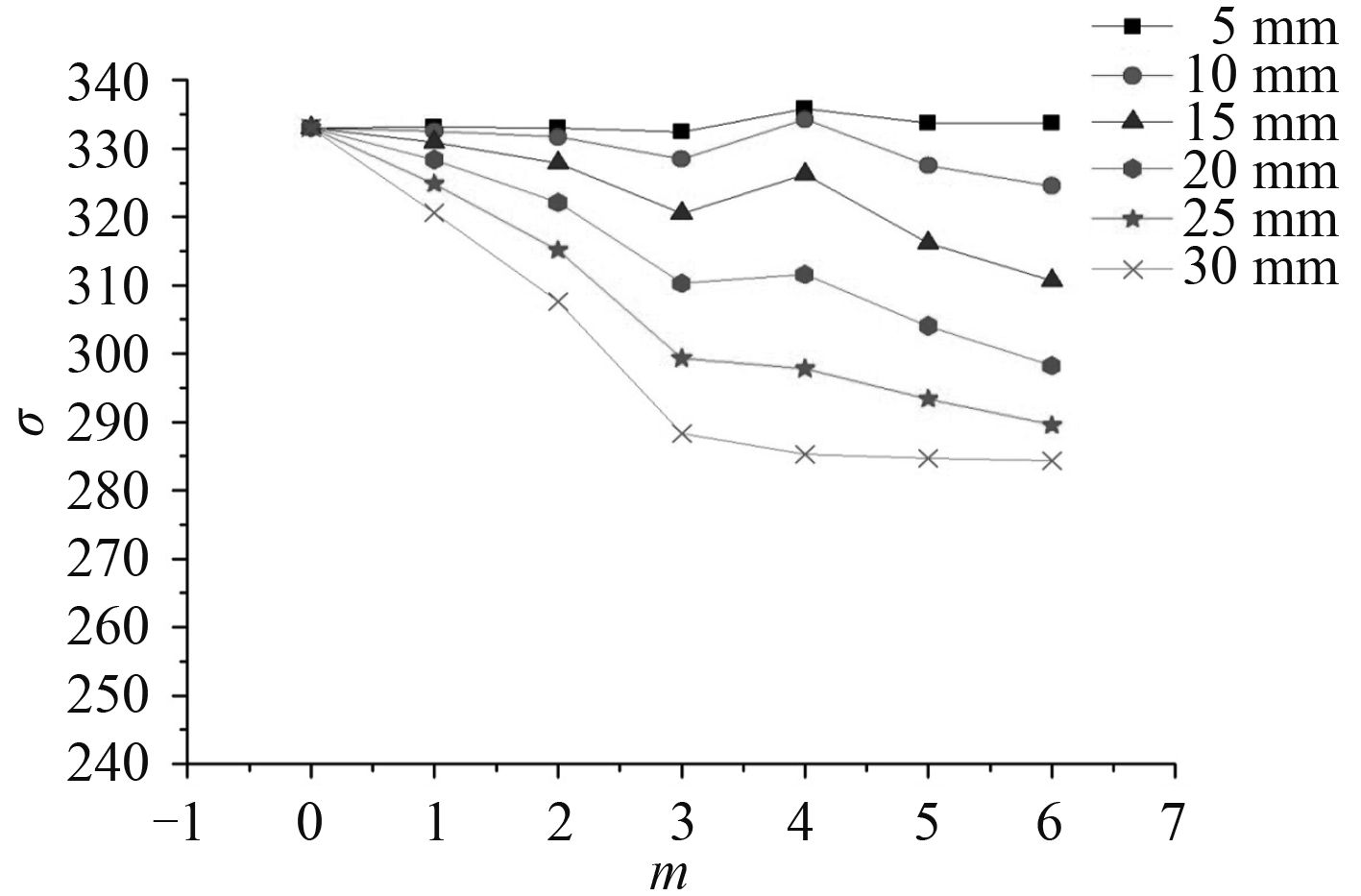
1.3.2 初始挠度半波数对加筋板弹性失稳压力的影响

由于计算数据较多，考虑初始挠度半波数对弹性失稳压力的影响，只选取了含幅值为 5 mm，10 mm，15 mm，20 mm，25 mm和 30 mm初始挠度的数据进行分析，如图 4所示。

图 4显示了当初始挠度幅值不变时，增加初始挠度的半波数，加筋板的弹性失稳压力的变化情况。从图中可以清晰地看出，不同的初始挠度情况下，弹性失稳压力整体的变化规律相似，都是随着半波数的增加而减小。在半波数不超过 3 的情况下，弹性失稳压力的变化率随半波数增大逐渐增大，当初始挠度幅值越大，弹性失稳压力随半波数的变化率也增大；半波数大于 3 的情况下，弹性失稳压力变化率减小。当半波数为 4 时，弹性失稳压力会突然变大，但是这种作用随着初始挠度幅值的增大而逐渐减小并消失。

2 初始挠度影响因子确定

由计算可知，含初始挠度的加筋板的弹性失稳压力与不含初始挠度加筋板的值存在一定差距。后者与前者差值反映了初始挠度对加筋板弹性失稳压力的影响，定义两者差值与后者的比值为影响因子 $\phi $ ，即

$\phi = \frac{{\text{差值}}}{{\text{正常加筋板临界应力}}}\text{，}$

(4)

相关文献已经对含有初始缺陷的加肋圆柱壳理论失稳压力的修正系数进行了研究^{[9 –10]}，参考其研究内容，可以初步确定影响因子与加筋板的长宽比、板厚、加强筋间距等几何尺寸有关。下面将分析含初始挠度加筋板弹性失稳压力与各主要尺寸参数的关系，计算模型是利用第 2 节的有限元模型作为基础，进行相应的参数改变。根据对中修船体甲板变形的勘验测量数据可知，船体加筋板出现的初始挠度幅值大部分在 10 mm左右，具有 1 个半波形式，因此只讨论含有幅值 10 mm、具有 1 个半波初始挠度的加筋板的影响因子。

2.1 加筋板长宽比与影响因子的关系

根据相关对船体加筋板尺寸的统计数据^[11]，船体加筋板板长 a 与加强筋间距 s 的比值应该满足关系： $2 \leqslant a/s \leqslant 6$ 。因此，控制加强筋间距保持不变，主要通过改变加筋板的长度 a 来改变加筋板的长宽比 $a/b$ 。

已知加筋板计算模型加强筋间距 $s = 400\;{\rm{mm}}$ ，具有 6 根加强筋，加筋板宽度 b = 2 800 mm所以加筋板长度取值范围为 $800 \leqslant a \leqslant 2\;400$ ，均匀取值：800 mm，1 000 mm，1 200 mm，1 400 mm，1 600 mm，1 800 mm，2 000 mm，2 200 mm，2 400 mm。经过计算可以得到影响因子如表 2。可以将表 2数据放在直角坐标系中显示，如图 5所示。

从图 5中可以看出，随着加筋板长宽比a/b的变化，影响因子 $\phi $ 的数值都出处在 0.996 到 1 的范围之内，且变化趋势趋于平缓，即影响因子变化率会保持在 0.4% 以内。由此可以确定，加筋板长宽比对影响因子的作用可以忽略不计，即加筋板长宽比对其极限承载力的影响可以忽略。

2.2 加筋板厚度与影响因子的关系

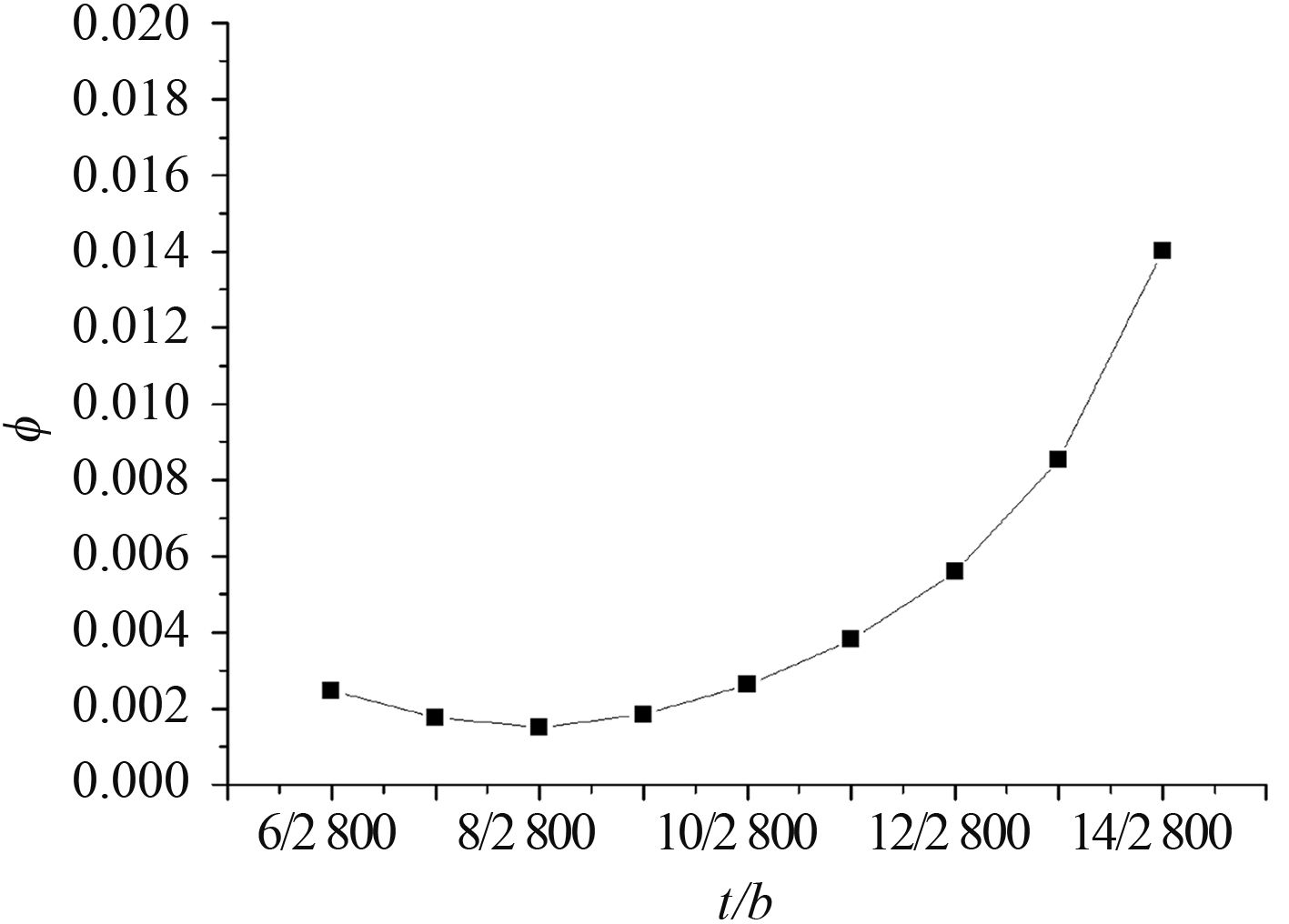
船用加筋板的厚度一般在 8 mm左右，对于特殊的大型船舶和军船，加筋板的厚度可能会超过 10 mm。因此，加筋板的厚度在 6 mm到 14 mm之间均匀取值进行计算，计算结果见表 3。为了保持变量为无量纲因子，将加筋板厚度 t 与加筋板宽度 b 的比值作为因变量。将计算结果绘制成图，如图 6所示。

从图 6可以看出，随着加筋板厚度 t 的增大，影响因子 $\phi $ 先减小然后增大，变化规律可以近似看成二次函数的关系。利用Matlab可以得到拟合的二次函数关系：

$\phi {\rm{ = }}278\,\,0{\left( {t/b} \right)^2} - 16.29\left( {t/b} \right) + 0.025\,\,02\text{。}$

(5)

拟合函数数据与原始数据最大误差为 0.1% 左右，符合工程要求。拟合函数符合实际情况。利用拟合函数可以确定影响因子最小点，设计过程中在最小点附近取值板厚，可以保证较小的影响因子。

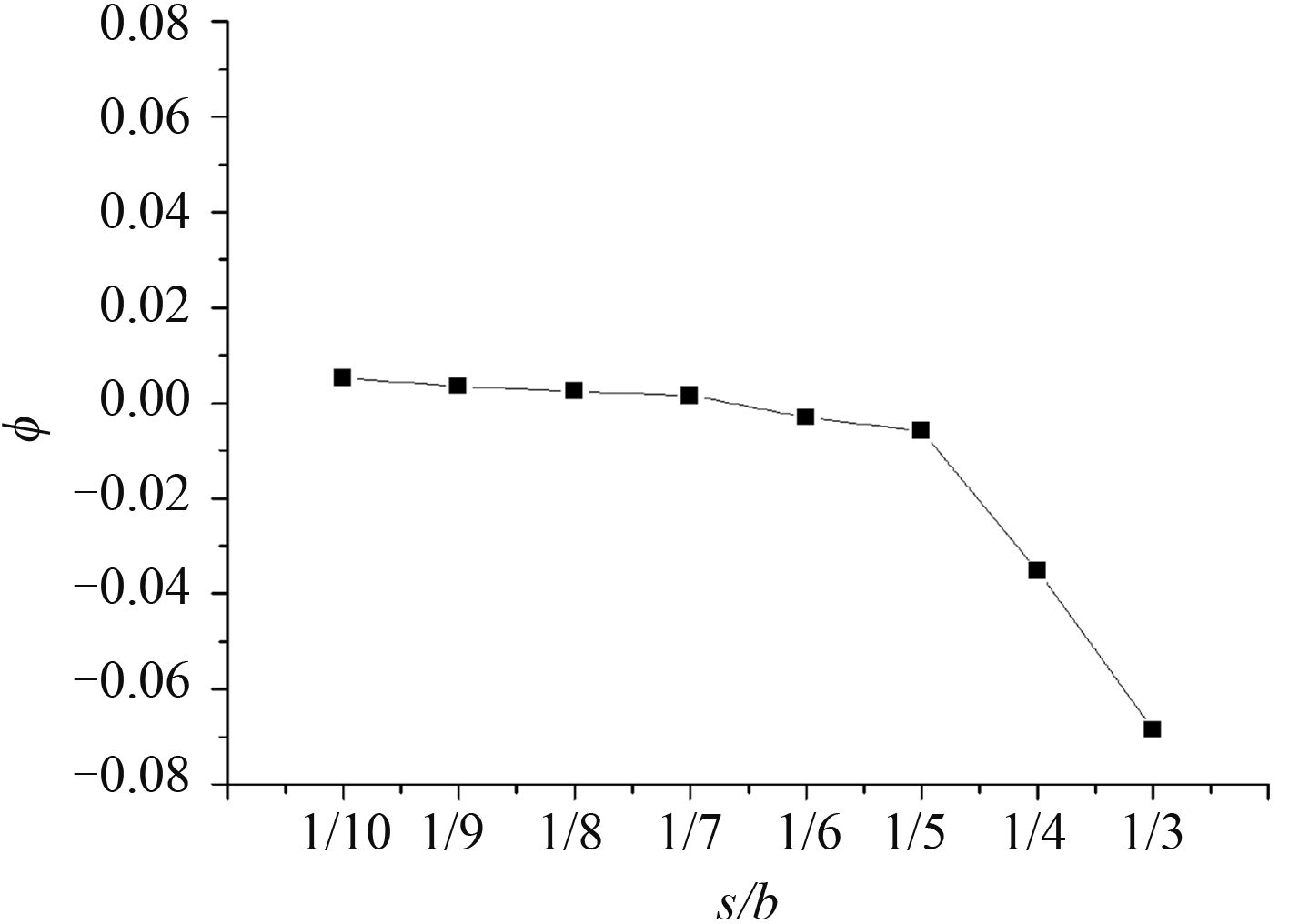
2.3 加强筋间距与影响因子的关系

考虑加强筋间距对影响因子 $\phi $ 的影响，对加强筋间距的控制，主要是通过改变加强筋的数量来实现，即保持加筋板的宽度 b 保持不变。根据统计规律，船用加筋板上加强筋一般在 2 根以上。因此，加筋板数量取 2~9 进行计算，计算结果见表 4。为了保持变量为无量纲因子，将加强筋间距 s 与加筋板宽度 b 的比值作为因变量。将计算结果绘制成图，如图 7所示。

从计算数据可看出，随着加强筋间距的增大，影响因子 $\phi $ 也逐渐减小，并出现负值，即加筋板的稳定性增强。根据图 7可得，当加强筋间距较小时，即 s/b 小于 1/7 时，影响因子的变化率较小。所以，对于密加筋板，加强筋间距对影响因子的影响作用可以忽略不计。当加强筋间距比较大时，初始挠度对加筋板的稳定性具有一定的增强作用。这就说明，当加筋板产生初始挠度之后，加强筋对稳定性的作用减弱，而在实际加筋板设计过程中，加强筋用于增强其稳定性，因此，可以综合考虑初始挠度和加强筋对稳定性的作用进行设计。

3 结　语

1）初始挠度对加筋板的弹性失稳压力影响较大，且随着初始挠度的幅值和半波数的增加，弹性失稳压力不断变小。

2）对于含有某种初始挠度的加筋板，其影响因子主要受加筋板的厚度和加强筋间距的影响，加筋板的长宽比影响较小，可以忽略。

3）影响因子的确定方法，满足工程要求，具有一定的可行性，可应用于船舶结构设计，完善结构设计规范。