在研究环肋圆柱壳总稳定性过程中,有的研究学者认为,当肋骨尺寸增大到一定程度后,继续增大肋骨尺寸,并不能显著提高圆柱壳的总稳定性,而增设纵骨才能有效提高其总稳定性[1 –4]。进一步的研究还表明[4 –5],在通常情况下,加设纵骨对圆柱壳总稳定的影响不明显,只有在壳体短、壳板薄、直径大的情况下才有效。加设纵骨对通常情况下的圆柱壳总稳定性影响不明显,未必对肋间壳板稳定性也影响不明显。有研究表明[6],通常情况下,加设纵骨可能是提高壳板稳定性更好的方法,因此需要深入研究纵骨对环肋圆柱壳肋间壳板稳定性的影响。
1 肋间壳板稳定性计算公式用能量法可以推导出环肋圆柱壳在轴向和横向压力联合作用下的总稳定性方程[7]:
| $\begin{split}\\[-12pt]& {T_1}{m^2}\alpha _1^2 + {T_2}\left( {{n^2} - 1} \right) = \frac{D}{{{R^2}}}{\left( {{m^2}\alpha _1^2 + {n^2} - 1} \right)^2} + \\& \quad \quad \quad \quad \frac{{Et{m^4}\alpha _1^4}}{{{{\left( {{m^2}\alpha _1^2 + {n^2}} \right)}^2}}} + \frac{{EI}}{{{R^2}l}}{\left( {{n^2} - 1} \right)^2}\text{。}\end{split}$ | (1) |
式中符号含义与文献[7]相同。
根据文献[5]的结论可以导出纵横加筋圆柱壳在轴向和横向压力联合作用下的总稳定性方程:
| $\begin{split}\\[-12pt]& {T_1}{m^2}\alpha _1^2 + {T_2}\left( {{n^2} - 1} \right) = \frac{D}{{{R^2}}}{\left( {{m^2}\alpha _1^2 + {n^2} - 1} \right)^2} + \\& \quad \quad \quad \quad \frac{{Et{m^4}\alpha _1^4}}{{{{\left( {{m^2}\alpha _1^2 + {n^2}} \right)}^2}}} + \frac{{EI}}{{{R^2}l}}{\left( {{n^2} - 1} \right)^2} + \frac{{EJ{m^4}\alpha _1^4}}{{{R^2}b}}\text{。}\end{split}$ | (2) |
式中: J 为计及带板的纵骨惯性矩; b 为纵骨间距。
参考文献[8],类似推导公式。可以求得,仅受轴向均匀压力作用下,环肋圆柱壳肋间壳板失稳临界压力公式和纵横加筋圆柱壳肋间壳板失稳临界压力公式为:
| $P_E^{(1)} \!= \!\frac{2}{{{m^2}{\alpha ^2}}}\left[ {\frac{D}{{{R^3}}}{{\left( {{m^2}{\alpha ^2} + {n^2} - 1} \right)}^2} + \frac{{Et{m^4}{\alpha ^4}}}{{R{{\left( {{m^2}{\alpha ^2}\! +\! {n^2}} \right)}^2}}}} \right]\text{,}$ | (3) |
| $\begin{split}\\[-12pt] P_{EL}^{(1)} = & \frac{2}{{{m^2}{\alpha ^2}}}\Biggr[ {\frac{D}{{{R^3}}}{{\left( {{m^2}{\alpha ^2} + {n^2} - 1} \right)}^2} + } \\[5pt]& \left. {\frac{{Et{m^4}{\alpha ^4}}}{{R{{\left( {{m^2}{\alpha ^2} + {n^2}} \right)}^2}}} + \frac{{EJ{m^4}{\alpha ^4}}}{{{R^3}b}}} \right]\text{。}\end{split}$ | (4) |
仅受横向均匀压力作用下,环肋圆柱壳肋间壳板失稳临界压力公式和纵横加筋圆柱壳肋间壳板失稳临界压力公式为:
| $P_E^{(2)}\! = \!\frac{1}{{{n^2} - 1}}\left[ {\frac{D}{{{R^3}}}{{\left( {{m^2}{\alpha ^2} + {n^2} - 1} \right)}^2} \!+\! \frac{{Et{m^4}{\alpha ^4}}}{{R{{\left( {{m^2}{\alpha ^2} + {n^2}} \right)}^2}}}} \right]\text{,}$ | (5) |
| $\begin{split}\\[-12pt] P_{EL}^{(2)} = & \frac{1}{{{n^2} - 1}} \Biggr[ {\frac{D}{{{R^3}}}{{\left( {{m^2}{\alpha ^2} + {n^2} - 1} \right)}^2} + } \\[5pt]& \left. {\frac{{Et{m^4}{\alpha ^4}}}{{R{{\left( {{m^2}{\alpha ^2} + {n^2}} \right)}^2}}} + \frac{{EJ{m^4}{\alpha ^4}}}{{{R^3}b}}} \right]\text{。}\end{split}$ | (6) |
向均匀压力作用下,环肋圆柱壳肋间壳板失稳临界压力公式和纵横加筋圆柱壳肋间壳板失稳临界压力公式为:
| $\begin{split}\\[-12pt] {P_E} = & \frac{1}{{0.5{m^2}{\alpha ^2} + {n^2} - 1}}\times \\& \left[ {\frac{D}{{{R^3}}}{{\left( {{m^2}{\alpha ^2} + {n^2} - 1} \right)}^2} + \frac{{Et{m^4}{\alpha ^4}}}{{R{{\left( {{m^2}{\alpha ^2} \!+\! {n^2}} \right)}^2}}}} \right]\text{,}\end{split}$ | (7) |
| $\begin{split}\\[-12pt] {P_{EL}} = & \frac{1}{{0.5{m^2}{\alpha ^2} + {n^2} - 1}}\Biggr[ {\frac{D}{{{R^3}}}{{\left( {{m^2}{\alpha ^2} + {n^2} - 1} \right)}^2} + } \\[5pt]& \left. {\frac{{Et{m^4}{\alpha ^4}}}{{R{{\left( {{m^2}{\alpha ^2} + {n^2}} \right)}^2}}} + \frac{{EJ{m^4}{\alpha ^4}}}{{{R^3}b}}} \right]\text{。}\end{split}$ | (8) |
引入参数
| $\begin{split}\\[-12pt] {P_E} = & \frac{{E \times {{10}^{ - 6}}}}{{0.5{m^2}{\alpha ^2} + {n^2} - 1}}\times\\[5pt]& \left[ {\frac{{{\gamma ^3}}}{{12(1 - {\mu ^2})}}{{\left( {{m^2}{\alpha ^2} + {n^2} - 1} \right)}^2}\! + \!\frac{{\gamma {m^4}{\alpha ^4} \times {{10}^4}}}{{{{\left( {{m^2}{\alpha ^2} + {n^2}} \right)}^2}}}} \right]\text{,}\end{split}$ | (9) |
| $\begin{split}\\[-12pt]{P_{EL}} = & \frac{{E \times {{10}^{ - 6}}}}{{0.5{m^2}{\alpha ^2} + {n^2} - 1}}\times\\& \left[ {\frac{{{\gamma ^3}}}{{12(1 - {\mu ^2})}}{{\left( {{m^2}{\alpha ^2}\! +\! {n^2} - 1} \right)}^2} \!+\! \frac{{\gamma {m^4}{\alpha ^4} \times {{10}^4}}}{{{{\left( {{m^2}{\alpha ^2} + {n^2}} \right)}^2}}} + \eta {m^4}{\alpha ^4}} \right]\text{。}\end{split}$ | (10) |
取
|
|
表 1 环肋圆柱壳的 m 和 n 值 Tab.1 m and n value for the ring-stiffened cylindrical shell |
对式(10)中的
|
|
表 2 纵横加筋圆柱壳的 m 和 n 值 Tab.2 m and n value for the longitudinal and transverse stiffened cylindrical shell |
从表 1可看出,环肋圆柱壳壳板失稳时,纵向失稳半波数
m = 1,周向失稳波数
n>10,且随着
根据式(9)、式(10)和相应式(3)~式(6)的变换式,编制计算机程序,可以绘制环肋圆柱壳肋间壳板失稳临界压力
图 1为
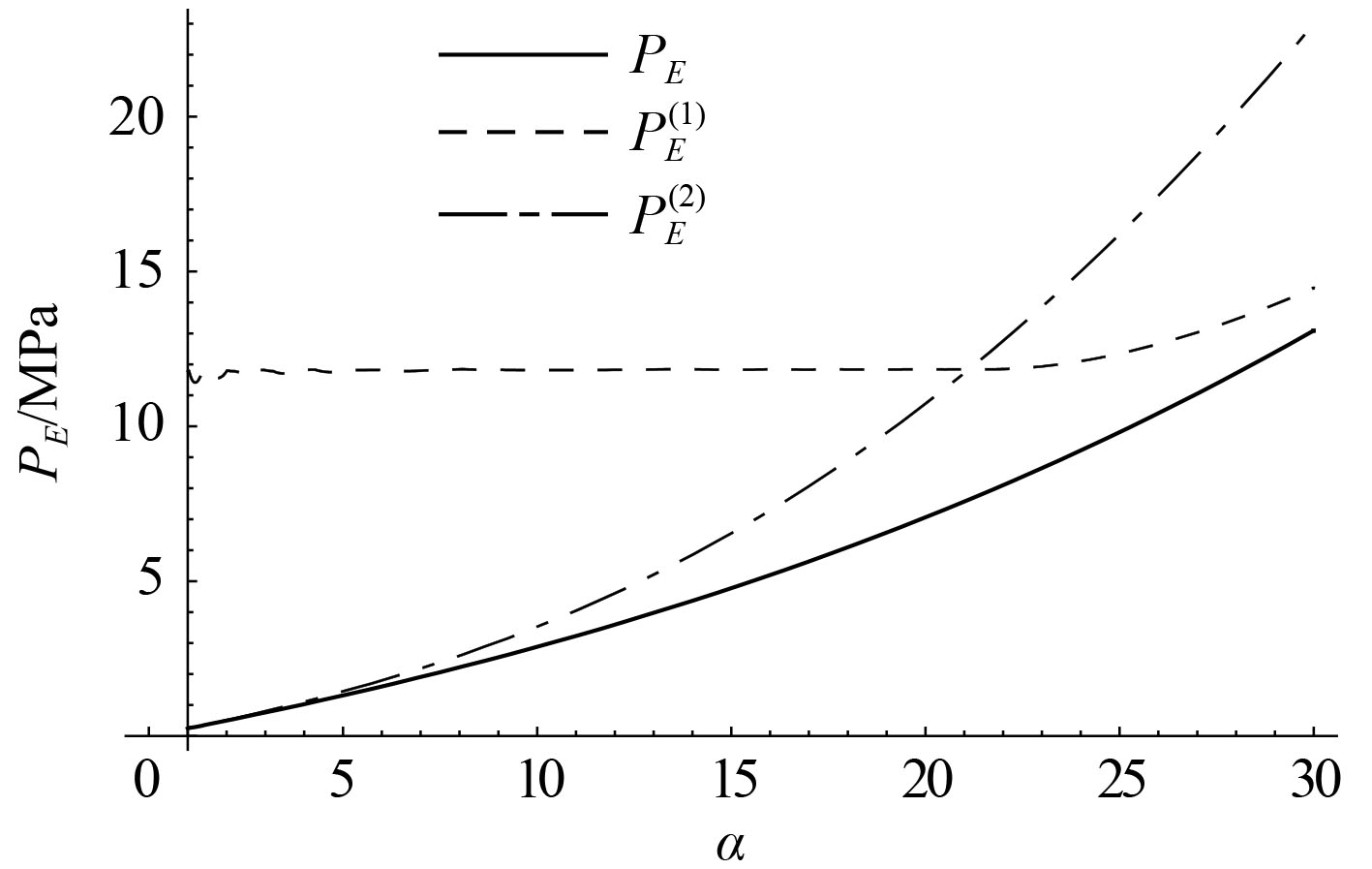
|
图 1
|
图 2是
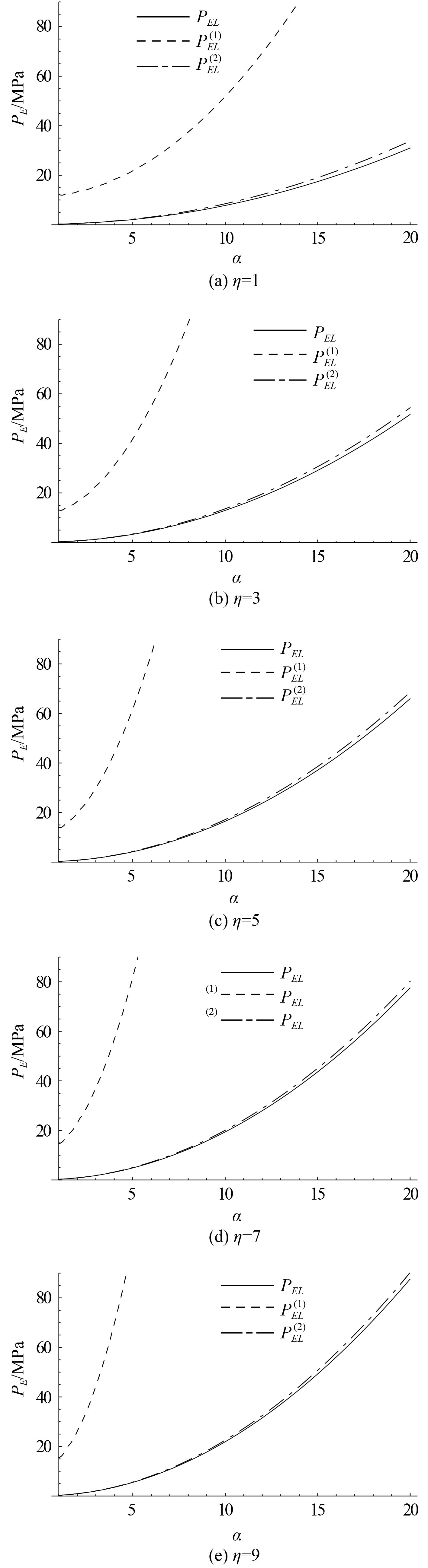
|
图 2
|
图 2是
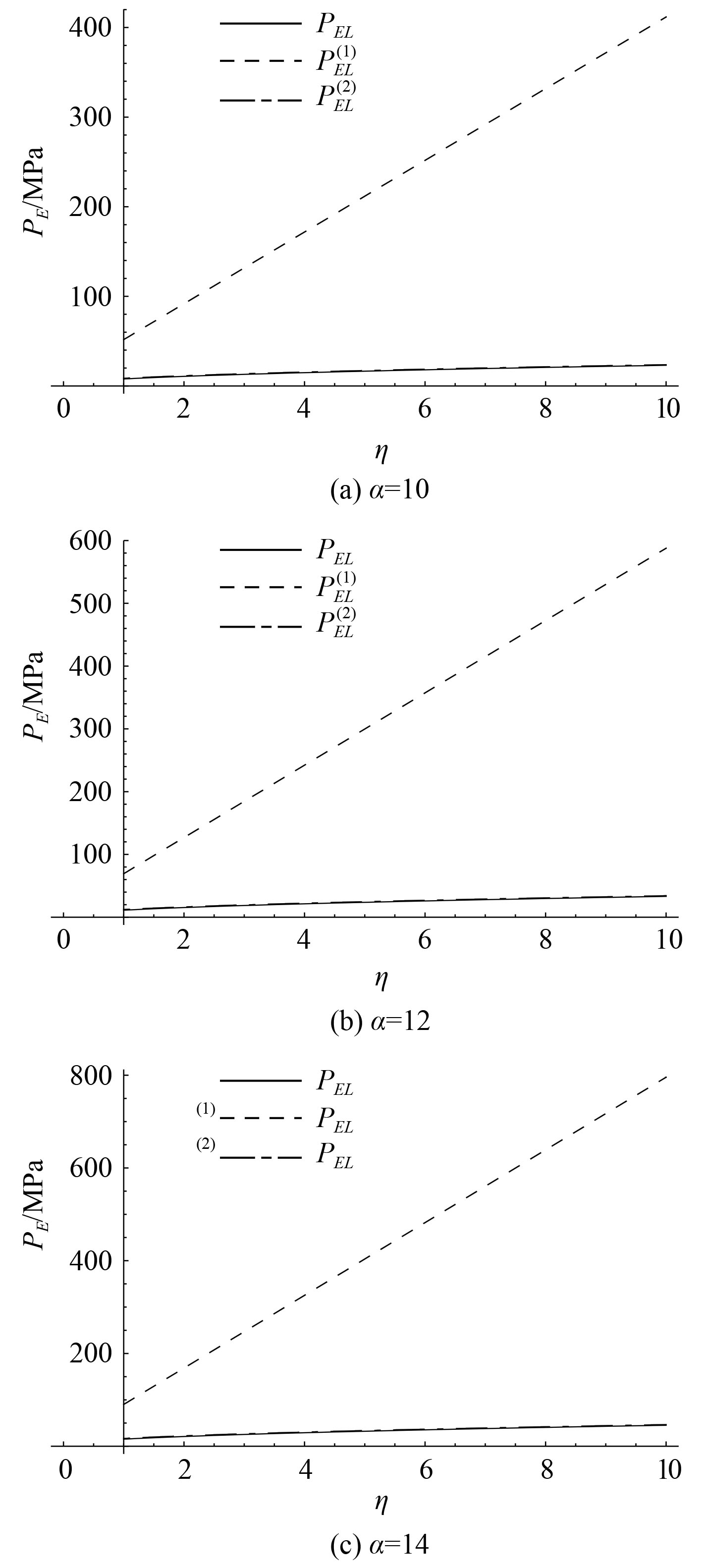
|
图 3
|
由图 1可看出,
由图 2得知,
图 3表明,
将图 1与图 2 ~
图 3比较可以发现,环肋圆柱壳加纵骨后,其肋间壳板稳定性明显提高。这一点也可以从表 1和表 2的对比中得到印证。以
式(7)或式(9)已经是成熟可靠的公式,不必做有限元计算验证。纵横加筋圆柱壳肋间壳板失稳临界压力计算式(8)或式(10)则处于研究讨论阶段,公式本身的准确性和上述计算方法的准确性尚不明确,需要用有限元计算来验证。
根据第3节中的基本数据,
边界条件:
| ${u_r} = {u_\theta } = {u_z} = 0(z = 0)\text{,}$ | (11) |
| ${u_r} = {u_\theta } = 0(z = l)\text{。}$ | (12) |
计算中均匀外压
有限元计算结果列于表 3。
|
|
表 3 失稳临界压力计算结果对比 Tab.3 Lose stability critical pressure calculation result contrast |
从表 3的对比可看出,公式计算的误差在 15% 范围以内,具有一定的可靠性。
5 结 语1)环肋圆柱壳肋间壳板失稳时,纵向失稳半波数
m = 1,周向失稳波数
n>10。加设纵骨后成为纵横加筋圆柱壳,肋间失稳时,纵向失稳波数
m = 1,周向失稳波数
n>10,且
n 比环肋圆柱壳的大。纵骨尺寸越大,即
2)环肋圆柱壳失稳临界压力
3)纵横加筋圆柱壳肋间失稳临界压力
4)环肋圆柱壳加设纵骨后,其肋间失稳临界压力明显提高,
5)式(8)或式(10)计算结果与有限元计算结果相比,误差在 15% 以内,数据的变化趋势二者相同。
| [1] |
王晓天, 邓剑平, 宁林, 等. 环肋圆柱壳稳定特性与破坏模式的探讨[J]. 哈尔滨工程大学学报, 1997 (6): 13–21.
Wang Xiaotian, Den Jianping, Ning Lin, et al. A study of the stability features and bulking pattern of the ring-stiffened cylindrical shell[J]. Journal of Harbin Engineering University, 1997 (6): 13–21. |
| [2] |
谢祚水, 许辑平. 潜艇薄壁大半径圆柱壳的总稳定性[J]. 中国造船, 1994 (2): 82–88.
Xie Zuoshui, Xu Jiping. On the overall stability of submarine circular cylindrical shells with large diameters and thin thicknesses[J]. Shipbuilding of China, 1994 (2): 82–88. |
| [3] |
谢祚水. 环肋圆柱壳稳定特性研究[J]. 中国造船, 1998 (4): 73–80.
Xie Zuoshui. Stability study of ring-stiffened circular cylindrical shell[J]. Shipbuilding of China, 1998 (4): 73–80. |
| [4] |
王林, 谢祚水. 纵横加肋耐压圆柱壳结构稳定性[J]. 造船技术, 1998 (2): 23–25.
Wang Lin, Xie Zuoshui. Stability of longitudinal and transverse stiffened cylindrical shell structure[J]. Technology of Shipbuilding, 1998 (2): 23–25. |
| [5] |
谢祚水. 受均匀外压力作用的圆柱壳结构形式的初步探讨[J]. 镇江船舶学院学报, 1990, 4 (4): 31–37.
Xie Zuoshui. Preliminary study of structure type of circular cylindrical shell under uniform external pressure[J]. Journal of Zhenjiang Shipbuilding Institute, 1990, 4 (4): 31–37. |
| [6] |
谢祚水, 王志军. 潜艇耐压圆柱壳结构的优化设计[J]. 中国造船, 1993, 12 : 23–25.
Xie Zuoshui, Wang Zhijun. Optimum design of circle cylindrical pressure shell for submarine[J]. Shipbuilding of China, 1993, 12 : 23–25. |
| [7] |
许辑平. 潜艇强度[M]. 北京: 国防工业出版社.1980.
XU Ji-ping. Strength of Submarine[M]. Beijing: National Defense Industry Press, 1980. |
| [8] |
王小明. 肋距对环肋圆柱壳壳板稳定性的影响[J]. 中国舰船研究, 2013, 8 (6): 81–84.
Wang Xiaoming. The influence of frame interval on the stability of ring-stiffened cylindrical shells[J]. Journal of Ship Research, 2013, 8 (6): 81–84. |
 2017, Vol. 39
2017, Vol. 39
