潜艇的机械噪声来源于艇内各种机械振动,螺旋桨噪声由轴激起壳体振动产生。对低速巡航的潜艇控制其振动产生的噪声是潜艇声学控制的重要方向。为控制潜艇的结构噪声,通常需进行结构声学计算,找到结构振动与辐射噪声的关系。圆柱壳的理论分析表明,通过对圆柱壳的振动模式与声辐射模式分析,可为圆柱壳结构的噪声控制提供理论依据。实际的潜艇结构是非标准圆柱壳,基于圆柱壳的波数谱分析难以应用,为此本文提出了在艇外建立分析圆柱面,在此圆柱面上设置声场,并采用波数谱法建立分析圆柱面声场与声辐射的关系判断艇的声辐射机理。
求解流体中的潜艇结构振动及计算声辐射时涉及到流固耦合问题,在求解此类问题时常采用的数值计算法包括有限元法和结构有限元耦合流体边界元法以及无限元法。圆柱壳是潜艇的结构原型,国内外学者在研究水下结构受激振力振动与声辐射问题时,常选取加有纵肋或横肋的单层壳体或双层壳体的圆柱壳模型。周其斗[1]在《细长壳体水声辐射问题的有限元结合边界元解法》提出了关于任意形状圆柱壳结构振动和声辐射问题的结构有限元耦合流体边界元(FEM/BEM)的附加质量附加阻尼算法,文中给出了有限元动力响应方程,为计算环肋的双层壳体结构振动与声辐射和船体结构的远场声辐射的问题提供指导思想。纪刚等[2]在《圆柱壳的力辐射模态与噪声控制》中采用结构有限元耦合流体边界元(FEM/BEM)的计算方法,应用DAMP语言编程,通过商业软件Nastran针对圆柱壳进行结构振动与声辐射分析,并应用力辐射模态理论解释圆柱壳振动辐射噪声受激振力加载方式的影响,提出了控制圆柱壳辐射噪声的方法。陈美霞,洛东平[3]通过数值计算法计算了加载简谐激振力下的在无限长圆柱障板中两端简支的有限长表面敷设声阻尼材料的环肋圆柱的振动与声辐射,并与实验结果对比,验证了辐射阻尼材料对抑制壳体振动和声辐射行之有效。上述文献中介绍的结构有限元耦合流体边界元法都是成熟有效的求解水下结构振动和声辐射的数值计算方法。本文在求解潜艇结构在水下的振动和辐射噪声是采用此类方法。
波数谱法是指通过傅立叶变换将在时域上的波场分解为频率-波数域上波分量的叠加。使用波数谱法分析圆柱壳振动时,将圆柱壳的振动分量视作在周向和轴向上具有不同波数的行进波的叠加,分析波传播的频率、波长、波数、传递能量特性[4]。L.H.Donnel在《Structure-Born Sound》一书中建立在柱面坐标系下的细长圆柱体的辐射声场,通过求解湿表面法向速度连续性边界条件下的Helmholtz方程给出了关于声压和法向速度的第 2 类汉克函数表达式[5]。C.Wang在文献[6]中提出由于曲率效应,柱面波的传递特性偏离平面波,并分析了环频率和临街频率在柱面波传递过程中产生的影响,分别给出在波数域下的声学薄壳与声学厚壳的振动和声辐射规律[7]。Soedel W在《Vibrations of shells and plates》一书中建立了圆柱壳上均方法相速度与辐射声功率之间的关系并给出了波数域下各模态速度功率与辐射声功率之间的传递效率[7]。
本文的工作是用波数谱法分析潜艇模型的声辐射规律。由于实际潜艇模型外形为水滴形,表面附着指挥台围壳,尾舵等复杂结构,为非标准圆柱形结构,无法对其结构表面的振动物理量通过波数谱法在轴向和周向上分解成具有不同波数的规则行进波的叠加。根据在理想流体中的能量守恒定律,建立一围绕艇模型的同轴虚拟圆柱面称作分析圆柱面,在分析圆柱面上得到的辐射声功率等于潜艇的辐射声功率。对分析圆柱面上的时间-空间信号通过波数分解变换为频率-波数信号,并建立柱面声压值与辐射声功率之间的关系。
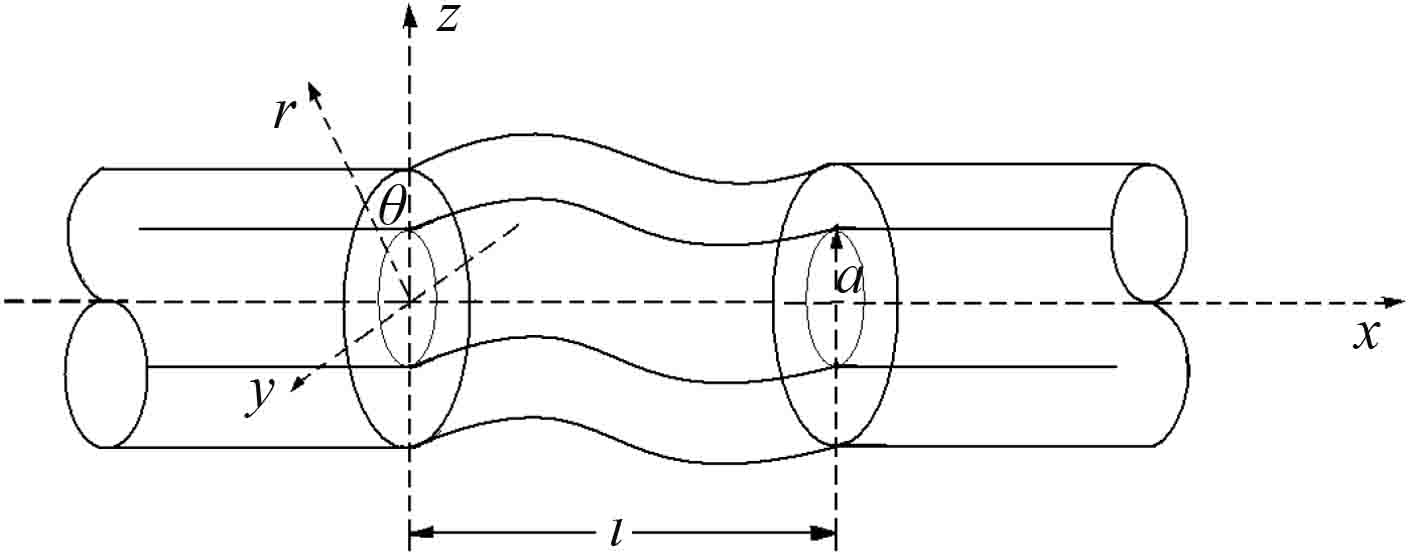
1 求解分析圆柱面上辐射声功率的方法在工程上为了更好地解决有限长圆柱形结构振动和声辐射问题,国内外学者常使用如图 1所示的柱坐标系,并建立无限长圆柱壳模型取其中有限长的振动扰动代替有限长圆柱壳做声辐射分析。文献[3 –7]采用此模型,在波数域上表达圆柱壳的振动及其辐射的声功率:利用波数变换的方法,有限长圆柱面的振动可以在具有障屏的无限圆柱面上展开为一系列规则振动的叠加。对每一规则波,可给出与之对应的辐射声场和声功率表达式;总的声功率表达为各规则波所辐射声功率的叠加,各规则波振动对噪声的贡献也相互独立。在本文的分析中截取无限长圆柱面上有限长的一段作为分析圆柱面,在分析圆柱面上做声辐射分析。如图所示,内层为结构,外层为分析圆柱面。
|
图 1 分析圆柱面及结构模型 Fig. 1 The model of analysis cylindrical surface and structure |
在省去时间项后,针对声压的幅值进行讨论,柱面坐标系下的Helmholtz方程:
| $\frac{{{\partial ^2}p}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial p}}{{\partial r}} + \frac{1}{{{r^2}}}\frac{{{\partial ^2}p}}{{\partial {\theta ^2}}} + \frac{{{\partial ^2}p}}{{\partial {x^2}}} + {k_0}^2p = 0\text{,}$ | (1) |
自由域中无穷远处声场需满足辐射边界条件:
| $p \sim \frac{1}{{\sqrt r }}{e^{ - i{k_0}r}},r \to \infty \text{。}$ | (2) |
在湿表面上有边界条件,流体质点速度与结构在该点处的法向速度一致,理想介质中流体质点速度与声压关系应满足声学运动方程:
| $ - j\omega {\rho _0}v = \frac{{\partial p}}{{\partial r}}\text{,}$ | (3) |
联立以上 3 个方程,Helmholtz方程有一般解:
| $p(r,\theta ,x) = {p_1}(r){p_2}(\theta ){p_3}(x)\text{。}$ | (4) |
假设声场中的轴向和周向周期分量分别为
则方程(1)可以表达为:
| $\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {p_1}(r)}}{{\partial r}}} \right) + \left[ {k_0^2 - k_x^2 - {{\left( {\frac{n}{r}} \right)}^2}} \right]{p_1}(r) = 0\text{。}$ | (5) |
此方程是Bessel方程,方程的一般解是第一类Bessel函数和Neumann函数的线性组合:
| ${p_1}(r) = A{J_n}\left[ {{{\left( {k_0^2 - k_x^2} \right)}^{1/2}}r} \right] + B{Y_n}\left[ {{{\left( {k_0^2 - k_x^2} \right)}^{1/2}}r} \right]\text{。}$ | (6) |
待定系数
A、
B 可通过在
r 到
当分析圆柱面的半径增大时,且
| $\begin{split}\\[-12pt]p = & A\left[ {{J_n}\left( {{{\left( {k_0^2 - k_x^2} \right)}^{1/2}}r} \right) - j{Y_n}\left( {{{\left( {k_0^2 - k_x^2} \right)}^{1/2}}r} \right)} \right]\times\\& \cos ({k_x}x)\cos (n\theta - {\phi _r})\text{。}\end{split}$ | (7) |
式中
| $v = - \frac{1}{{j\omega {\rho _0}}}\frac{{\partial p}}{{\partial r}} = \frac{{j{k_r}A}}{{\omega {\rho _0}}}\frac{{d{H_n}({k_r}r)}}{{d({k_r}r)}}\cos ({k_x}x)\cos (n\theta - {\phi _r}),$ |
总辐射声功率由各模态
| ${\tilde W_n} = \int\limits_0^{ + \infty } {\left[ {\tilde W(n,{k_x})} \right]} \cdot {\rm{d}}{k_x}$ | (8) |
利用Bessel函数和Neumann函数的微分特性,分析圆柱面上每一辐射模态
| ${\tilde W_{rad}}(n,{k_x}) = \int_{ - \infty }^{ + \infty } {\int_0^{2\pi } {p_{n,{k_x}}^2\frac{{\pi k_r^2{{H'}_n}^2({k_r}r)}}{{2{\rho _0}\omega }}{r^2}} {\rm{d}}\theta } {\rm{dx}}\text{。}$ | (9) |
假设分析圆柱面包裹的结构为单层圆柱壳结构,壳体湿表面上有流体介质质点速度与结构表面法向速度一致,根据连续性方程(3)建立的声压和结构法向位移之间的关系,其中圆柱壳半径为 a,湿表面法向位移为:
| $w\left( {x,\theta ,t} \right) = \tilde w\cos ({k_x}x)\cos (n\theta - {\phi _r}){e^{j\omega t}}\text{,}$ | (10) |
| ${\omega ^2}{\rho _0}\tilde w = A{\left( {k_0^2 - k_x^2} \right)^{1/2}}{H'_n}\left[ {{{\left( {k_0^2 - k_x^2} \right)}^{1/2}}a} \right]\text{,}$ | (11) |
解得系数 A:
| $A = \frac{{{\omega ^2}{\rho _0}\tilde w}}{{{{\left( {k_0^2 - k_x^2} \right)}^{1/2}}H{{_n^{}}^\prime }\left[ {{{\left( {k_0^2 - k_x^2} \right)}^{1/2}}a} \right]}},$ |
将系数 A 代回方程(10)中可得湿表面声压:
| $p(a,\theta ,x) = \frac{{{\omega ^2}{\rho _0}\tilde w}}{{{k_r}}}\frac{{H_n^{(2)}\left( {{k_r}a} \right)}}{{H{{_n^{(2)}}^\prime }\left( {{k_r}a} \right)}}\cos ({k_x}x)\cos (n\theta - {\phi _r})\text{,}$ | (12) |
下面求解圆柱壳各振动模态
| $\ \,\!\!{\tilde W_{rad}}(n,{k_x}) \!\!= \!\!\left\{\!\!\!\! \begin{array}{l}\frac{{{\omega ^3}{\rho _0}{{\left| {\tilde w} \right|}^2}}}{{k_r^2{{\left| {H{{_n^{(2)}}^\prime }\left( {{k_r}a} \right)} \right|}^2}}}\int_{ - \infty }^{ + \infty } {{{\cos }^2}} ({k_x}x){\rm{d}}x{\rm{ , }}n = 0\text{,}\\[15pt]\frac{{{\omega ^3}{\rho _0}{{\left| {\tilde w} \right|}^2}}}{{2k_r^2{{\left| {H{{_n^{(2)}}^\prime }\left( {{k_r}a} \right)} \right|}^2}}}\int_{ - \infty }^{ + \infty } {{{\cos }^2}} ({k_x}x){\rm{d}}x{\rm{ , }}n \ne 0\text{。}\end{array} \right.\!\!\!\!$ | (13) |
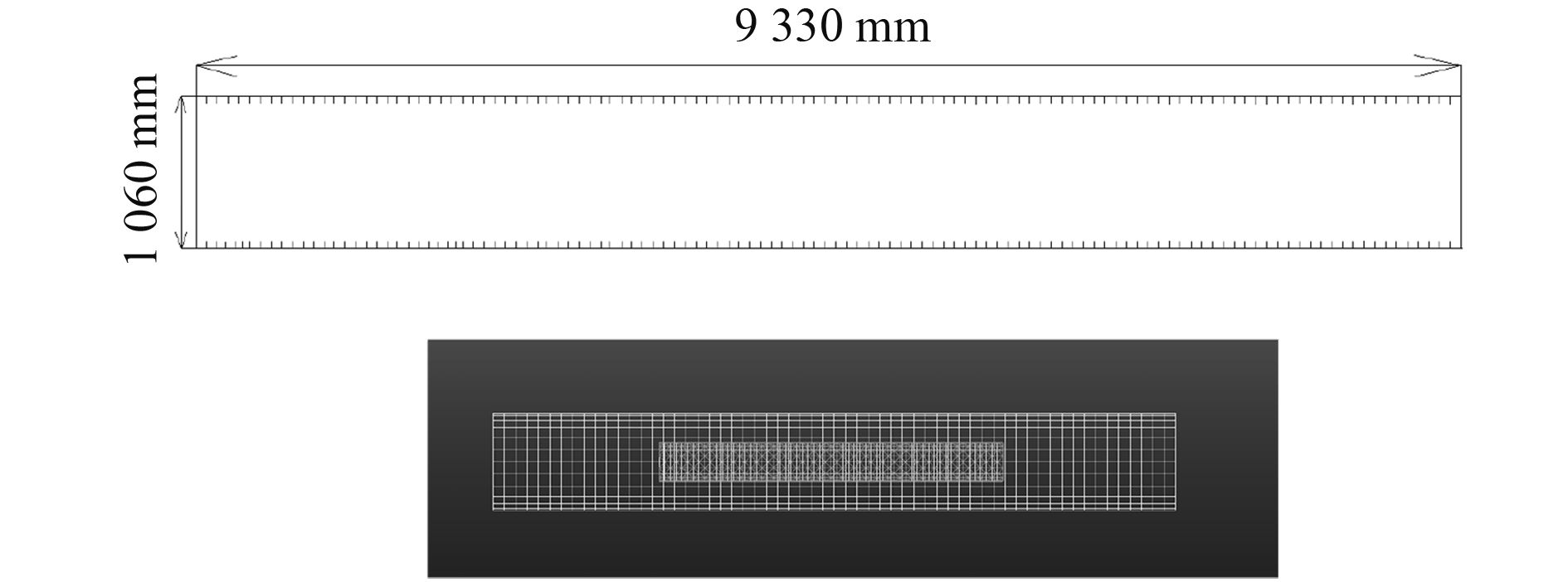
对分析圆柱面上使用波数谱法求解声功率时,采用带有肋骨的圆柱壳模型进行验证。 图 2为圆柱壳模型,其主尺寸参数为长 9 330 mm,半径 530 mm,柱壳板厚 4 mm,端盖板厚 4 mm,均匀布置肋骨 60 根,肋骨厚 3 mm。分析圆柱面与圆柱壳同轴,长 195 000 mm,半径 1 500 mm。分析在某肋骨上加载垂向单位激振力下的声辐射。
|
图 2 圆柱壳尺寸及有限元结构 Fig. 2 Data of the cylinder and FE model |
|
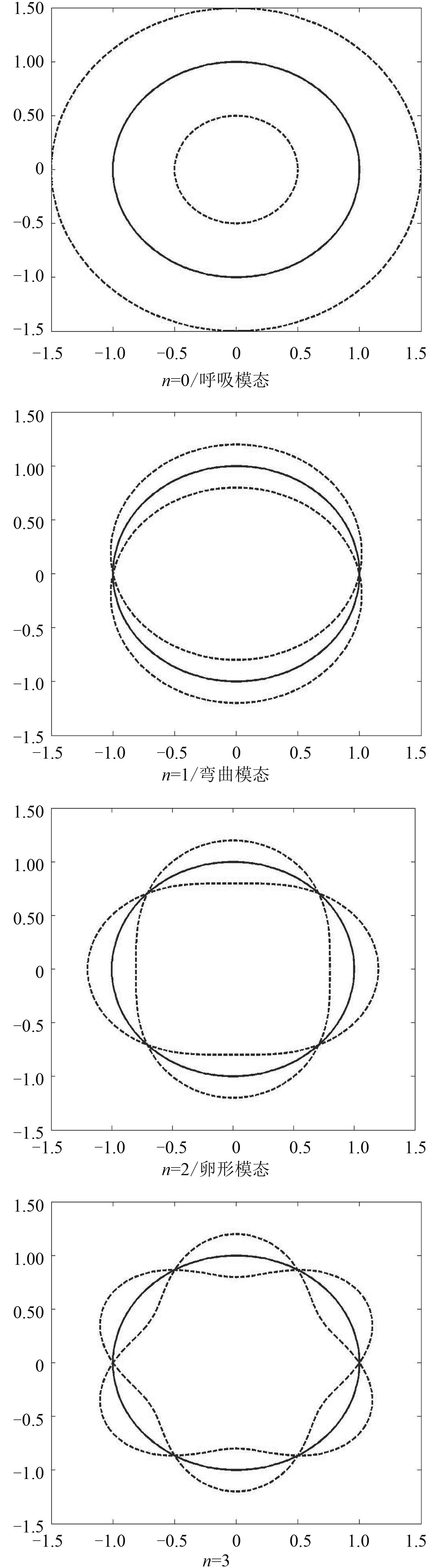
图 3 前 4 阶辐射模态波形 Fig. 3 The first 4-order radiation mode waveform |
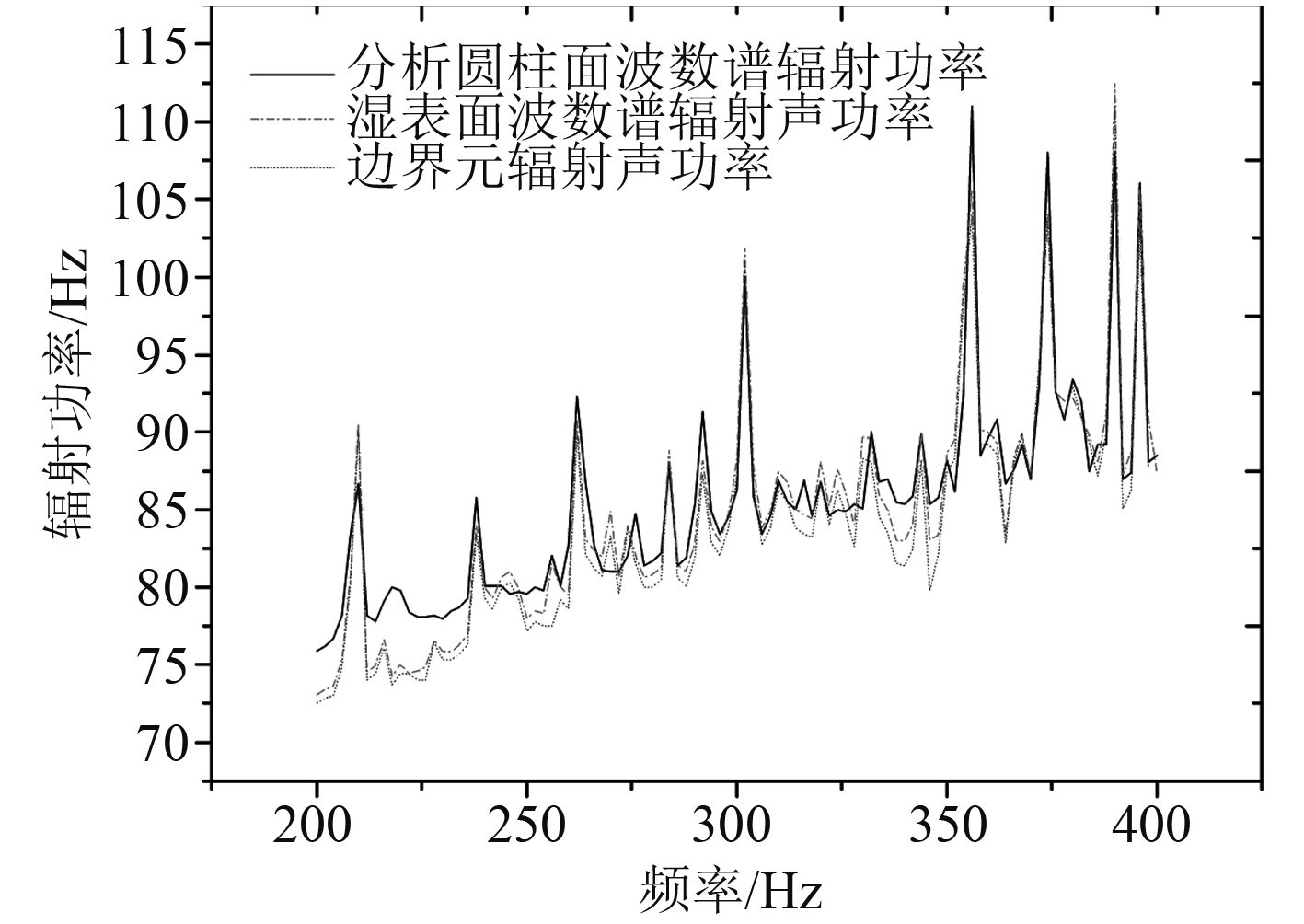
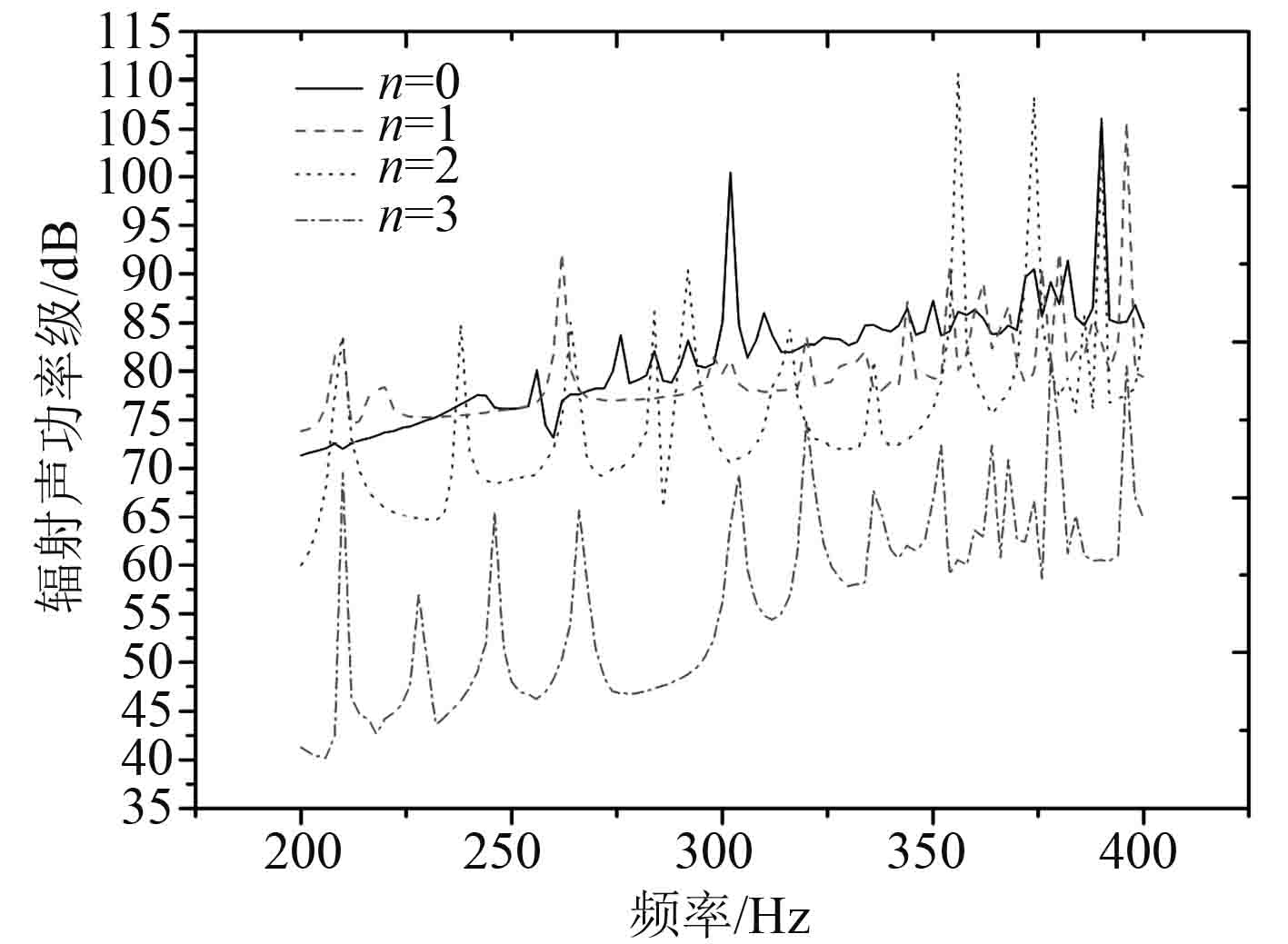
图 3给出了圆柱壳振动进行周向分解后的前四阶振动模态,其中 n 表示周向波数。 图 4给出了辐射声功率随时间的变化曲线,图中的点虚线是在湿表面上利用法向速度和声压求解的辐射声功率,点划线是在湿表面上采用式(8)叠加周向波数小于 16 的振动波得到,实线是在分析圆柱面上采用式(8)叠加前 16 个周向辐射模态得到。在湿表面上采用波数谱法求解的辐射声功率与湿表面直接积分求解辐射声功率的曲线拟合程度较高,谭路在其文章中已就该观点进行论证[4]。在分析圆柱面上求解的辐射声功率在 300 Hz以下略高于在湿表面上直接求解的辐射声功率,在 300 Hz到 400 Hz之间误差减小,部分频率点处湿表面声功率高于分析圆柱面声功率。整体上峰值处误差小于声功率级较小处频点的误差。 图 5给出了分析圆柱面上周向前 4 阶辐射模态的辐射声功率级随频率的变化曲线,可得在 200 Hz到 400 Hz的频率区间内主要辐射模态为 n = 0, n = 1, n = 2,其中 n = 0 模态的辐射声功率整体上大于其他模态,而 9 个主要辐射波峰分别由 3 个辐射模态主导。 图 6给出了在湿表面应用波数谱上通过均方法相速度的积分求解的前4阶辐射声功率级,可得到其声功率的变化规律与分析圆柱面上整体一致,前 3 阶为声功率的主要辐射模态,同时是柱壳的主要振动模态[6]。 n = 0 模态的辐射声功率占主导,在 200 Hz到 400 Hz频域中几个波峰的主要振动模态皆为 n = 0。结合图 5和图 6验证了在分析圆柱面上的主要辐射模态在整体上与圆柱壳结构振动模态基本一致,在个别频率点处辐射模态偏离振动模态。
|
图 4 湿表面与分析圆柱面辐射声功率对比 Fig. 4 Acoustic radiation power on wet surface and analysis cylindrical surface |
|
图 5 分析圆柱面前 4 阶辐射声功率 Fig. 5 The first 4-order radiation mode on analysis cylindrical surface |

|
图 6 湿表面前 4 阶辐射声功率 Fig. 6 The first 4-order radiation mode on wet surface |
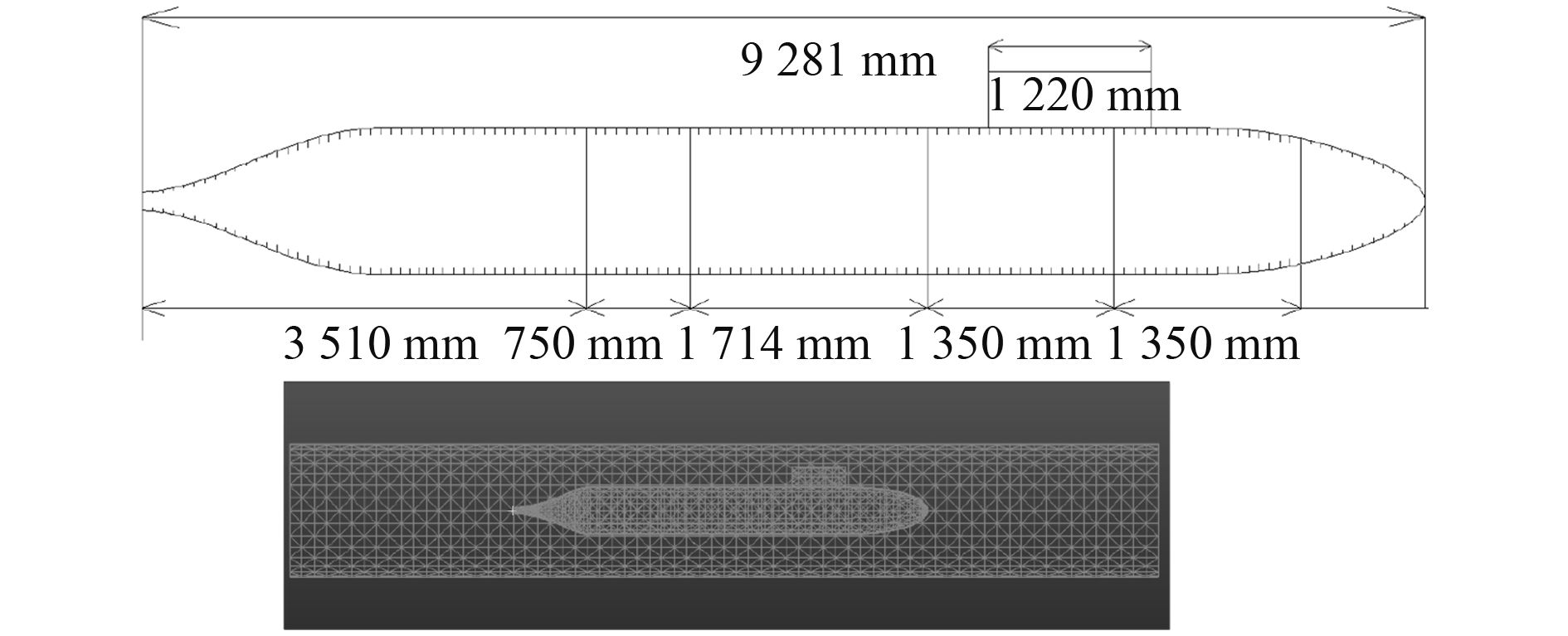
本节讨论稳态扫频单位垂向激振力加载到艇模型的频率响应。如图 1所示,艇模型总长 9 281 mm,最大直径 508 mm,指挥台围壳顶到轴线距离 460 mm。艇体为钢制结构,板厚 4 mm。振动载荷为正弦曲线,幅值 10 N,加载到艇壳某肋骨上。利用结构有限元耦合流体边界元法求解分析圆柱面声压值,用式(9)建立声压与辐射声功率之间的关系,假设在轴向上波数
|
图 7 模型艇尺寸及有限元结构 Fig. 7 Data of the submarine and FE model for the submarine model |
|
|
表 1 模型艇结构尺寸及材料参数和激振力、流体数据 Tab.1 Data of the submarine, force and fluid |
|
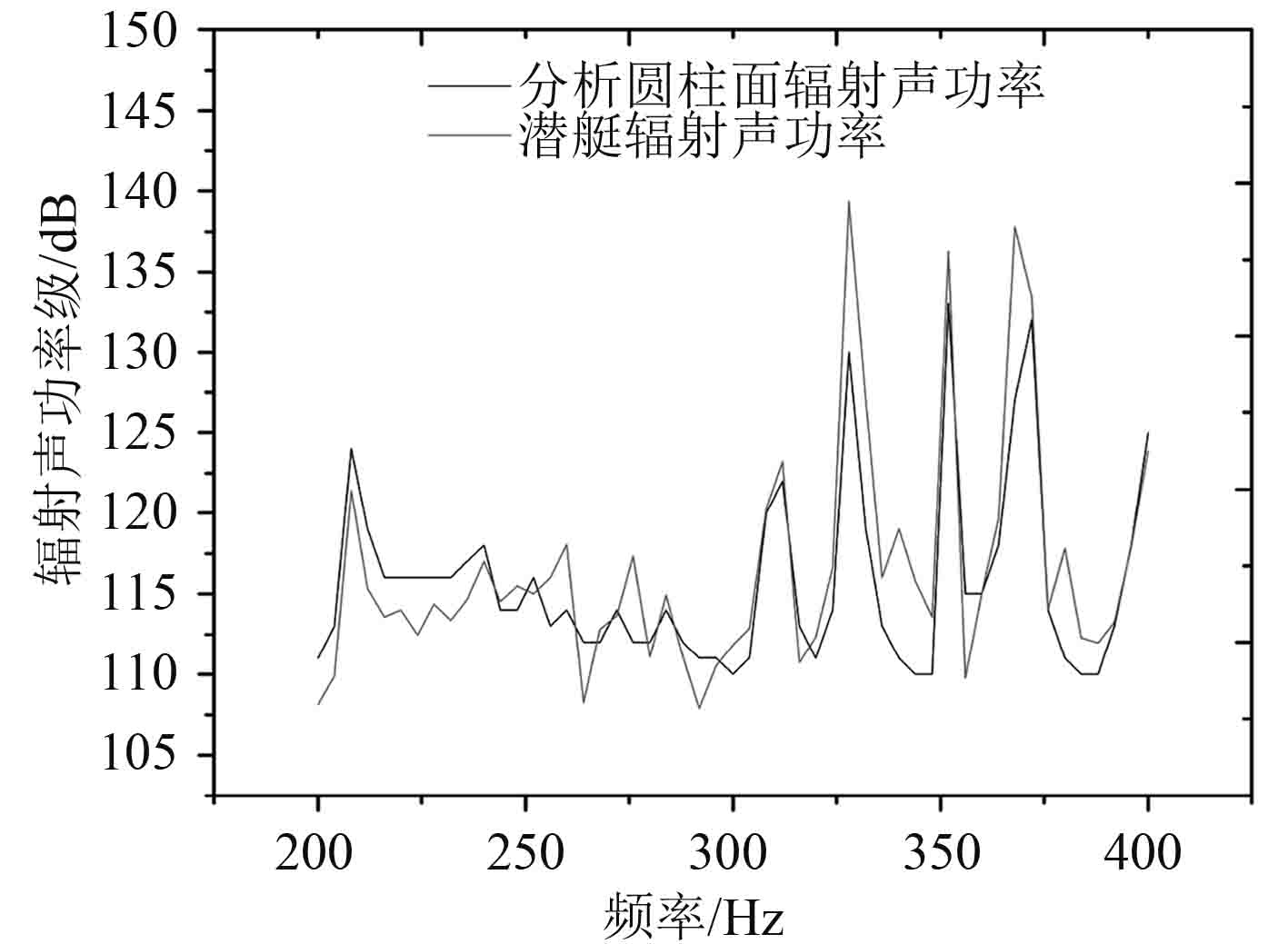
图 8 潜艇湿表面与分析圆柱面辐射声功率对比 Fig. 8 Acoustic radiation power on wet surface and analysis cylindrical surface of submarine |
|
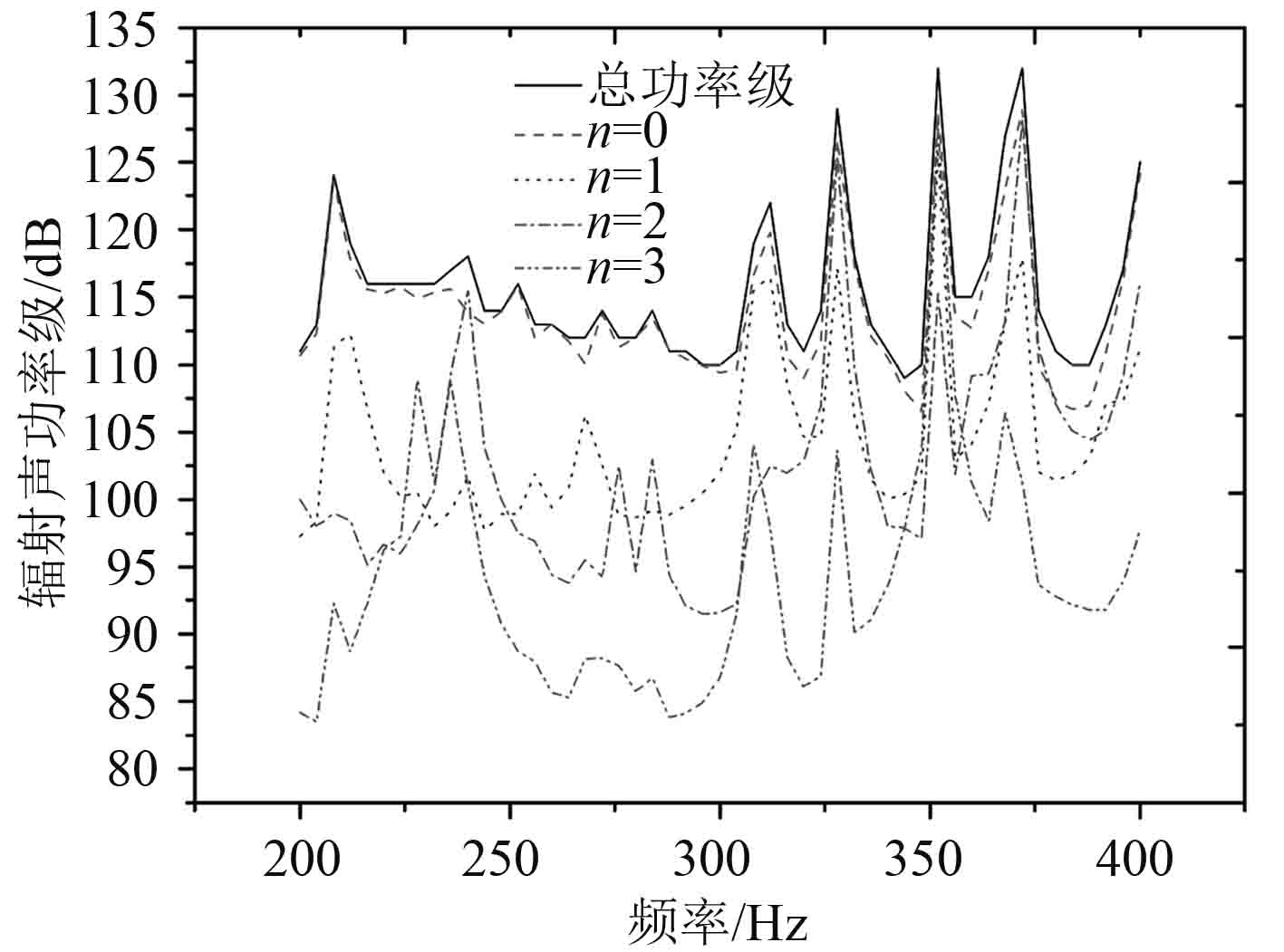
图 9 潜艇分析圆柱面前4阶辐射声功率 Fig. 9 The first 4-order radiation mode on analysis cylindrical surface of submarine |
图 8给出分析圆柱面辐射声功率与潜艇辐射声功率,曲线拟合程度较高,最大误差 13.7 dB。 图 9给出分析圆柱面上声压值经波数谱分解后利用式(8)解出的辐射声功率。得到潜艇在 200~400 Hz的频率区间内的主要辐射模态为 n = 0, n = 1, n = 3。由图 9可以看到,在 200~400 Hz这个频段内 n = 0、 n = 1的辐射模态起主要作用,分别为呼吸模态与弯曲模态。 n = 0 模态下辐射声功率在 200~400 Hz频段是最大的,几乎与总辐射声功率曲线重合,因而它是潜艇在该工况下总辐射噪声的主要成分,由于 n = 0 的噪声辐射主模式为呼吸辐射模态,该模态由壳体的呼吸振动引起,在前文中已得到验证;个别频率处,如 328 Hz,352 Hz,372 Hz等峰值频率, n = 0,1,2,3 模态的辐射声功率均与总功率相近。因此可以得出结论,要控制该工况下的圆柱壳在 200~400 Hz频段的辐射噪声控制应重点针对呼吸运动、弯曲振动进行,个别频率还需针对卵形和 n = 3 模态振动进行。
4 结 语本文使用波数谱法分析艇的声学辐射机理,在艇外围设计分析圆柱面,并放置声场,建立声压值与辐射声功率的关系。并在主尺寸与潜艇相似的标准圆柱壳上验证在分析圆柱面上使用波数分解方法分析其内部结构声辐射规律的可行性。通过分析辐射声功率的频率-波数谱,找到对总辐射声功率贡献较大的辐射模态,控制艇的总辐射声功率可通过控制产生该辐射模态的振动实现。本文为分析潜艇辐射噪声机理提供一种新的解决路径。
| [1] | 周其斗. 细长壳体水声辐射问题的有限元结合边界元解法[J]. 海军工程学院学报, 1996, 2 : 35–44. |
| [2] | 纪刚, 张纬康, 周其斗. 随机力作用下的水下结构声辐射分析[J]. 船舶力学, 2006, 10 (2): 153–159. |
| [3] | 陈美霞, 邱昌林, 骆东平. 基于FEM/BEM法的内部声激励水下圆柱壳声辐射计算[J]. 中国舰船研究, 2007, 2 (6): 50–54. |
| [4] | 谭路, 纪刚, 张玮康. 采用波数域方法分析细长柱壳的振动与声辐射[J]. 海军工程大学学报, 2013, 25 (3): 66–71. |
| [5] | Wang C, Lai J C S. Prediction of natural frequencies of finite length circular cylindrical shells[J]. Applied Acoustics, 2000, 59 : 385–400. DOI: 10.1016/S0003-682X(99)00039-0 |
| [6] | SOEDEL W.Vibrations of shells and plates[M]. Marcel Dekker, Inc., 1993. |
| [7] | CREMER L, HECKL M, PETERSSON B A T. Structure-Borne Sound[M]. Springer, Berlin: 2004. |
| [8] | BATHE K J. Finite element procedures[M]. Upper Saddle River: Prentice-Hall, 1996. |
| [9] | 杨剑, 张璞, 陈火红. 新编MD Nastran有限元实例教程[M]. 北京: 机械工业出版社, 1998. |
| [10] | 谢志勇, 周其斗, 纪刚. 双层柱壳的流固耦合模态计算与试验研究[J]. 海军工程大学学报, 2009, 21 (2): 97–101. |
| [11] | 陈锐. 潜艇结构振动辐射噪声分析研究[D]. 武汉: 华中科技大学, 2005. |
| [12] | 杜功焕, 朱哲民, 龚秀芬.声学基础[M]. 上海: 上海科技出版社, 1998. |
| [13] | 左言言, 徐凌, 鲍冬云, 等. 结构振动的频率-波数分析法[J]. 噪声与振动控制, 1996, 3 : 13–16. |
| [14] | Nilsson A C. Wave propagation in simple hull-frame structures of ship[J]. Journal of Sound and Vibration, 1976, 44 (3): 393–405. DOI: 10.1016/0022-460X(76)90510-1 |
| [15] | Von Flotow A H. Travelling wave control for large spacecraft structures[J]. J of Guidance, 1986, 9 (4): 462–468. DOI: 10.2514/3.20133 |
 2017, Vol. 39
2017, Vol. 39
