圆柱壳结构在工程中得到了广泛的应用,它的动态特性更是得到很多研究人员的持续关注[1]。对于圆柱壳的自由振动问题,通常的求解是基于位移方法,即根据圆柱壳的振动控制方程,引入一般位移表达式,然后再依据边界约束获得频率。对于圆柱壳沿长度方向的位移表达形式大致可以分成两类,即带指数项的精确表达式[2]和其他近似表达式(如梁函数[3]、多项式[4]等)。近似表达式仅仅能够满足某些边界条件,这种近似实际上会带来误差。
本文基于Flügge弹性薄壳理论[5],给出了自由振动频率和波数的精确解形式,并针对齐次边界条件推导了控制方程。通过联立振动控制方程和边界约束方程获得频率之后,本文再进一步研究了边界条件和频散曲线之间的关系,找出了频率-波数点在频散曲线上的位置。对于面内 2 种振动(轴向为主、环向为主)对应的高阶频率也进行了探讨。通过行列式曲线以及频散曲线研究了截止(起始)频率的 3 个区域,以及圆柱壳振动方式和这 3 个频率段的关系。
1 理论分析图 1给出了本文讨论的圆柱壳模型。壳体长度 L,中面半径 R,厚度 h。各向同性材料,弹性模量 E,泊松比 v,剪切模量 G,密度 ρ。壳体中面在坐标轴( x,φ,z)上位移分量分别为 u,v 和 w(向内为正)。
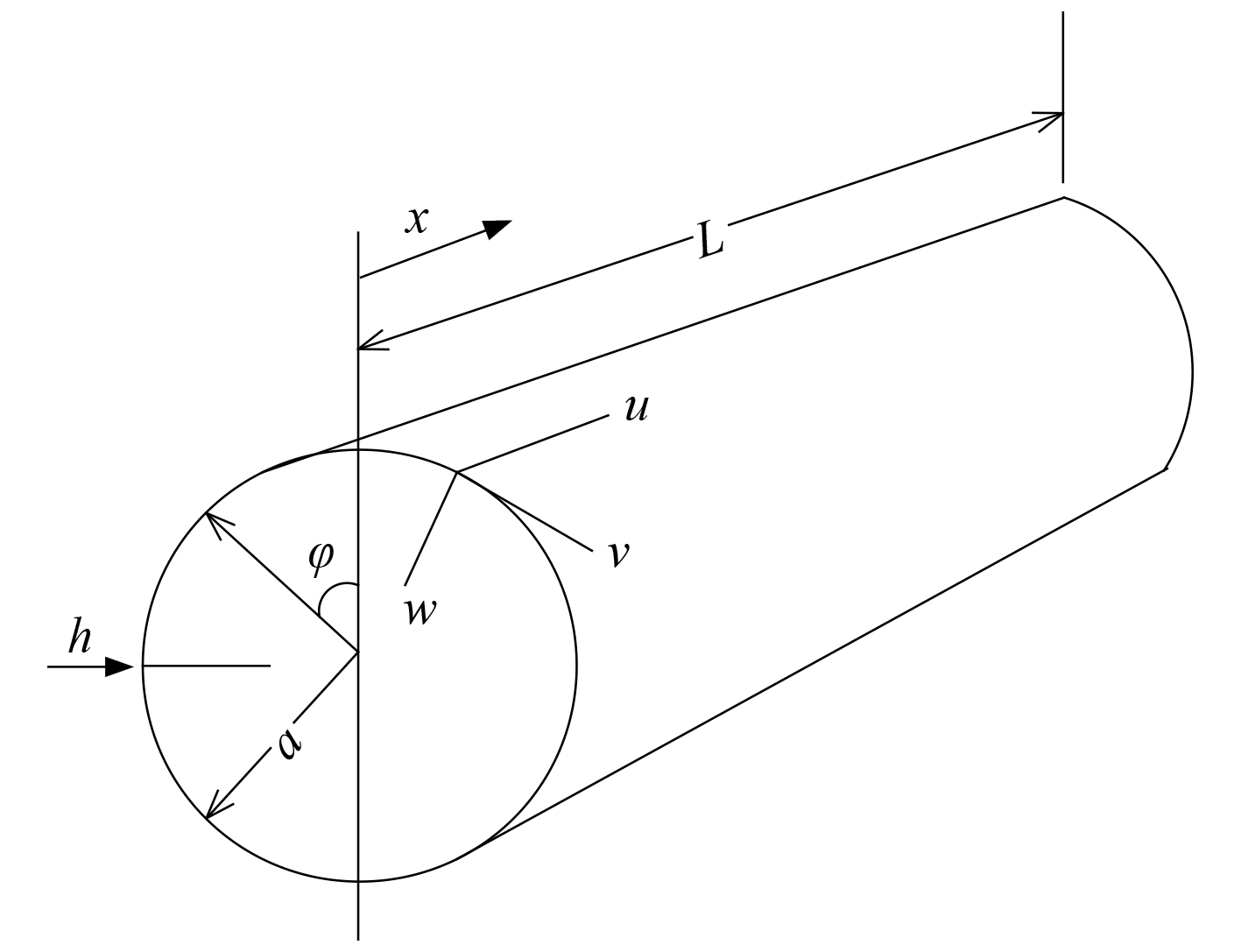
|
图 1 圆柱壳和坐标系 Fig. 1 Circular cylindrical shell and coordinate system |
基于Flügge弹性薄壳理论[5],圆柱壳的自由振动方程可以表示为如下矩阵形式:
| $\left[ {\begin{array}{*{20}{c}}{{L_{11}}}&{{L_{12}}}&{{L_{13}}}\\{{L_{21}}}&{{L_{22}}}&{{L_{23}}}\\{{L_{31}}}&{{L_{32}}}&{{L_{33}}}\end{array}} \right]\left\{ {\begin{array}{*{20}{c}}u\\v\\w\end{array}} \right\} = \frac{{\rho h{R^2}}}{B}\frac{\partial }{{\partial {t^2}}}\left\{ {\begin{array}{*{20}{c}}u\\v\\w\end{array}} \right\}\text{,}$ | (1) |
式中:
基于分离变量方法的思路,假设壳体振动的中面位移函数形式为:
| $\begin{array}{l}u(x,\phi ,t) = {U_0}{e^{\lambda x}}\cos (n\phi )\cos (\omega t)\text{,}\\[5pt]v(x,\phi ,t) = {V_0}{e^{\lambda x}}\sin (n\phi )\cos (\omega t)\text{,}\\[5pt]w(x,\phi ,t) = {W_0}{e^{\lambda x}}\cos (n\phi )\cos (\omega t)\text{。}\end{array}$ | (2) |
式中: U 0, V 0 和 W 0 为振幅; λ 为轴向波数; n 为周向波数; ω 为振动圆频率(1/s)。将式(2)代入式(1),可以得到如下矩阵形式的控制方程:
| $\left[ {\begin{array}{*{20}{c}}{{C_{11}}}&{{C_{12}}}&{{C_{13}}}\\{{C_{21}}}&{{C_{22}}}&{{C_{23}}}\\{{C_{31}}}&{{C_{32}}}&{{C_{33}}}\end{array}} \right]\left\{ {\begin{array}{*{20}{c}}{{U_0}}\\{{V_0}}\\{{W_0}}\end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}}0\\0\\0\end{array}} \right\}\text{。}$ | (3) |
其中方程(3)存在非零解的条件是系数行列式等于 0 ,即
| $\det \left( {\left[ C \right]} \right) = 0\text{。}$ | (4) |
式(4)即为圆柱壳自由振动的控制方程。该方程是关于圆柱壳几何参数以及材料参数的特征方程。该方程是关于轴向波数 λ 的 8 次方程或者频率 ω 的 6 次代数方程。
| ${g_8}{\lambda ^8} + {g_6}{\lambda ^6} + {g_4}{\lambda ^4} + {g_2}{\lambda ^2} + {g_0} = 0\text{,}$ | (5) |
| ${b_6}{\omega ^6} + {b_4}{\omega ^4} + {b_2}{\omega ^2} + {b_0} = 0\text{。}$ | (6) |
式中 g i ( i = 0,2,4,6,8), b j ( j = 0,2,4,6)为方程的系数。
设定圆柱壳的几何参数和材料参数,并假设环向振动波数 n 之后,方程(4)中未知数为轴向波数 λ 和频率 ω。
求解方程(5)可得到的 8 个精确解,这里简写为:
| $\begin{array}{*{20}{l}}\begin{array}{l}\lambda _{1,2}^2 = - \displaystyle\frac{{\sqrt {{a_6}} }}{2} + {a_8} - \frac{1}{2}\sqrt { - \frac{{{a_3}}}{{4\sqrt {{a_6}} }} + {a_9}}\text{,}\\[15pt]\lambda _{3,4}^2 = - \displaystyle\frac{{\sqrt {{a_6}} }}{2} + {a_8} + \frac{1}{2}\sqrt { - \frac{{{a_3}}}{{4\sqrt {{a_6}} }} + {a_9}}\text{,} \end{array}\\[30pt]\begin{array}{l}\lambda _{5,6}^2 = \displaystyle\frac{{\sqrt {{a_6}} }}{2} + {a_8} - \frac{1}{2}\sqrt {\frac{{{a_3}}}{{4\sqrt {{a_6}} }} + {a_9}}\text{,}\\[15pt]\lambda _{7,8}^2 = \displaystyle\frac{{\sqrt {{a_6}} }}{2} + {a_8} + \frac{1}{2}\sqrt {\frac{{{a_3}}}{{4\sqrt {{a_6}} }} + {a_9}}\text{。} \end{array}\end{array}$ | (7) |
式中 a i( i = 1~9)为参数。
方程(6)的 3 个根表示为:
| $\begin{array}{l}\omega _1^2 = {j_4} - \displaystyle\frac{{{2^{1/3}}{j_2}}}{{3{b_6}j_5^{1/3}}} + \frac{{j_5^{1/3}}}{{3 \times {2^{1/3}}{b_6}}},\\[15pt]\omega _2^2 = {j_4} + \displaystyle\frac{{\left( {1 + {\rm{i}}\sqrt 3 } \right){j_2}}}{{3 \times {2^{2/3}}{b_6}j_5^{1/3}}} - \frac{{\left( {1 - {\rm{i}}\sqrt 3 } \right)j_5^{1/3}}}{{6 \times {2^{1/3}}{b_6}}},\\[15pt]\omega _3^2 = {j_4} + \displaystyle\frac{{\left( {1 - {\rm{i}}\sqrt 3 } \right){j_2}}}{{3 \times {2^{2/3}}{b_6}j_5^{1/3}}} - \frac{{\left( {1 + {\rm{i}}\sqrt 3 } \right)j_5^{1/3}}}{{6 \times {2^{1/3}}{b_6}}}\text{。}\end{array}$ | (8) |
式中 j i( i = 1~5)为参数。
本文讨论圆柱壳的齐次边界条件,端部( x = 0, L)的边界条件包括位移和转角约束以及力、力矩约束[1],即
| $\begin{array}{l}u = 0,v = 0,w = 0,\partial w/\partial x = 0\text{,}\\[6pt]Nx = 0,{R_x} = 0,{S_x} = 0,Mx = 0\text{。}\end{array}$ | (9) |
将式(2)代入式(9)得到未知数轴向波数 λ 和频率 ω 的边界控制方程。
联立边界控制方程(9)和方程(4)就能求解齐次边界下圆柱壳的振动频率。先依据式(7)得到 8 个根,分别求出振型。
| ${\alpha _i} = \frac{{{U_{0i}}}}{{{W_{0i}}}},{\beta _i} = \frac{{{V_{0i}}}}{{{W_{0i}}}},i = 1,2 \ldots 8\text{。}$ | (10) |
根据式(10)的振型,改写式(2)的位移函数并代入边界条件(9),可以得到一个关于 W i 的 8 阶齐次方程组
| ${\left[ A \right]_{8 \times 8}}\left\{ W \right\} = \left\{ 0 \right\}\text{,}$ | (11) |
令系数矩阵 A 的行列式等于 0,则
| $\det \left( A \right) = 0\text{。}$ | (12) |
求得频率 ω。
式(12)是一个关于频率的超越方程。通常采用“扫频”方式求解,即设定一定的频率范围,依照一定的频率步长进行扫频计算。
2 数值算例和讨论本文讨论圆柱壳在齐次边界条件下的自振特性,数值算例的基本参数是: L = 0.4 m, R = 0.1 m, h = 0.004 m, E = 2.11 × 10 11 N/m 2, v = 0.3,考虑了 3 种典型的边界条件[1],即薄膜简支SD-SD(shear diaphragms),两端固定C-C(Clamped)和简支-固定(SD-C)。定义无量纲的频率参数为:
| ${\varOmega ^2} = \frac{{\rho {R^2}\left( {1 - {v^2}} \right)}}{E}{\omega ^2}\text{。}$ | (13) |
表 1给出了 3 种边界下的频率计算值。表中 m 为圆柱壳在轴向形成的振型半波数。
|
|
表 1 3 种边界下的频率参数 Ω 计算值 Tab.1 Frequency parameters, Ω for 3 boundary conditions |
圆柱壳的两端共有 8 个边界条件,根据式(9)能够组合成 136 种边界[1]。依据本文给出的算法计算过程稍显复杂,计算量也比较大。在分离变量的求解过程中,很多研究在轴向不采用指数项
圆柱壳的边界条件(9)是关于波数 λ 和频率 ω 两个未知量的方程。通过引入梁边界方程进行简化,式(9)就变成了仅仅关于波数 λ 的方程。这种简化过程实际上也是波传播方法的主要思路[6- 7]。与表 1中 3 种边界条件对应,梁横向振动的边界条件和频率方程见表 2[8]:
|
|
表 2 梁的边界条件和频率方程 Tab.2 Characteristic equations and roots for beam vibration |
如果不考虑边界条件式(9),方程(4)所表示的方程实际上就是圆柱壳的频散方程[7]。当 n = 2 时,波数 λ 和频率参数 Ω 的图形化显示见图 2。方程(4)有 8 个根,在圆柱壳的振动范围,它们的形式为:
| $\lambda = \pm {\lambda _1},\begin{array}{*{20}{c}}{}&{ \pm i{\lambda _2}}\text{,}&{}\end{array} \pm \left( {{\lambda _3} \pm i{\lambda _4}} \right)\text{。}$ | (14) |
其中,

|
图 2 频率 Ω 和波数 λ 的关系曲线 Fig. 2 Wave number in shells vs. frequency |
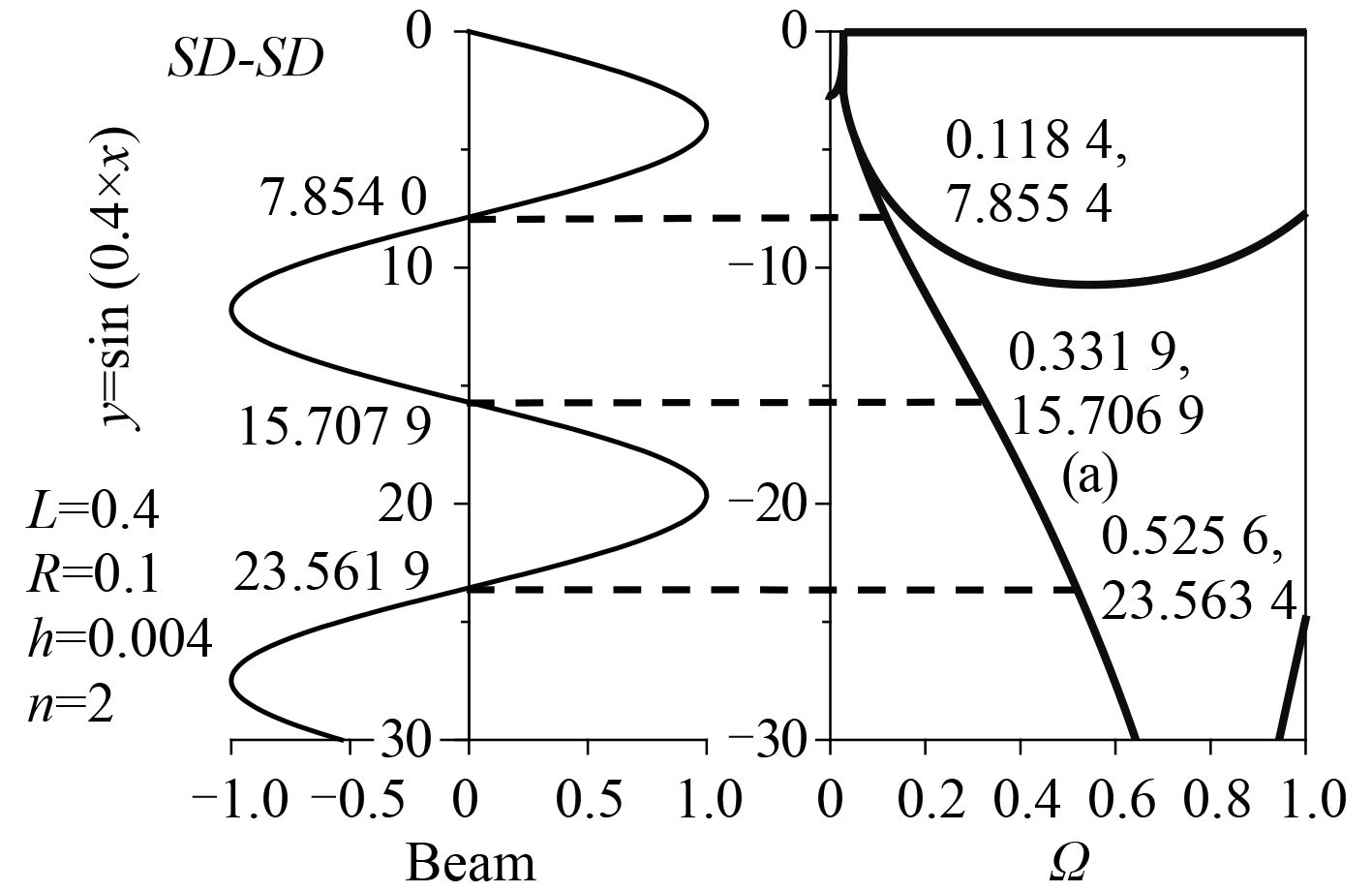
|
图 3 SD-SD 边界下频率的求解和比较 Fig. 3 Frequency determination for SD-SD |
从理论分析可知,圆柱壳的频率是通过式(4)和式(9)联立求解。对于式(4)添加边界条件约束式(9),那么频率点就会限定在这张图的某条分支曲线上。以
SD-SD 边界为例,对于
m = 1,2,3,
n = 2 时的 3 个频率分别为 0.118 4,0.331 9 和 0.525 6(参见表 1)。这 3 个频率对应的纯虚数解
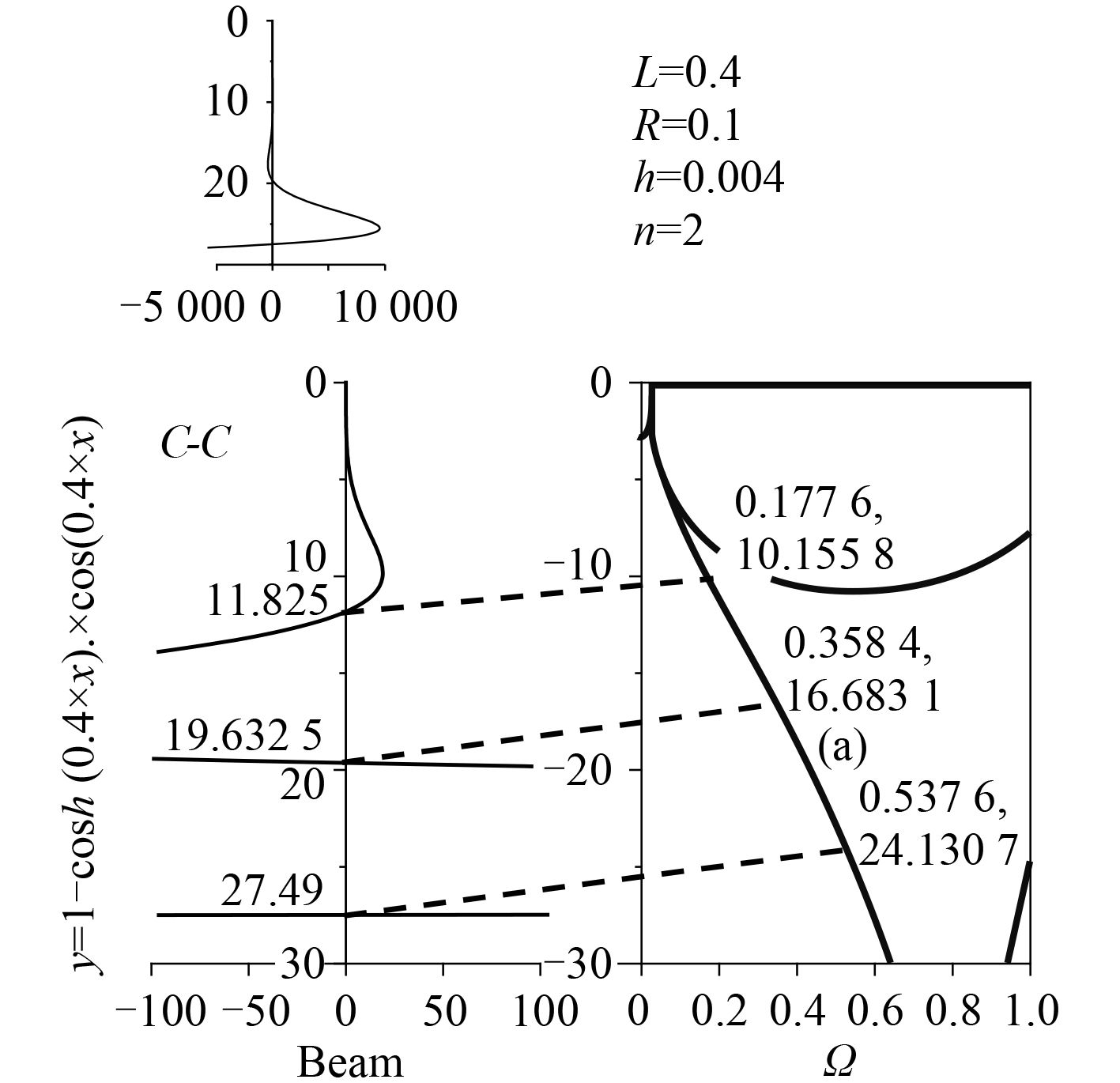
|
图 4 C-C 边界下的频率求解 Fig. 4 Frequency determination for C- C |
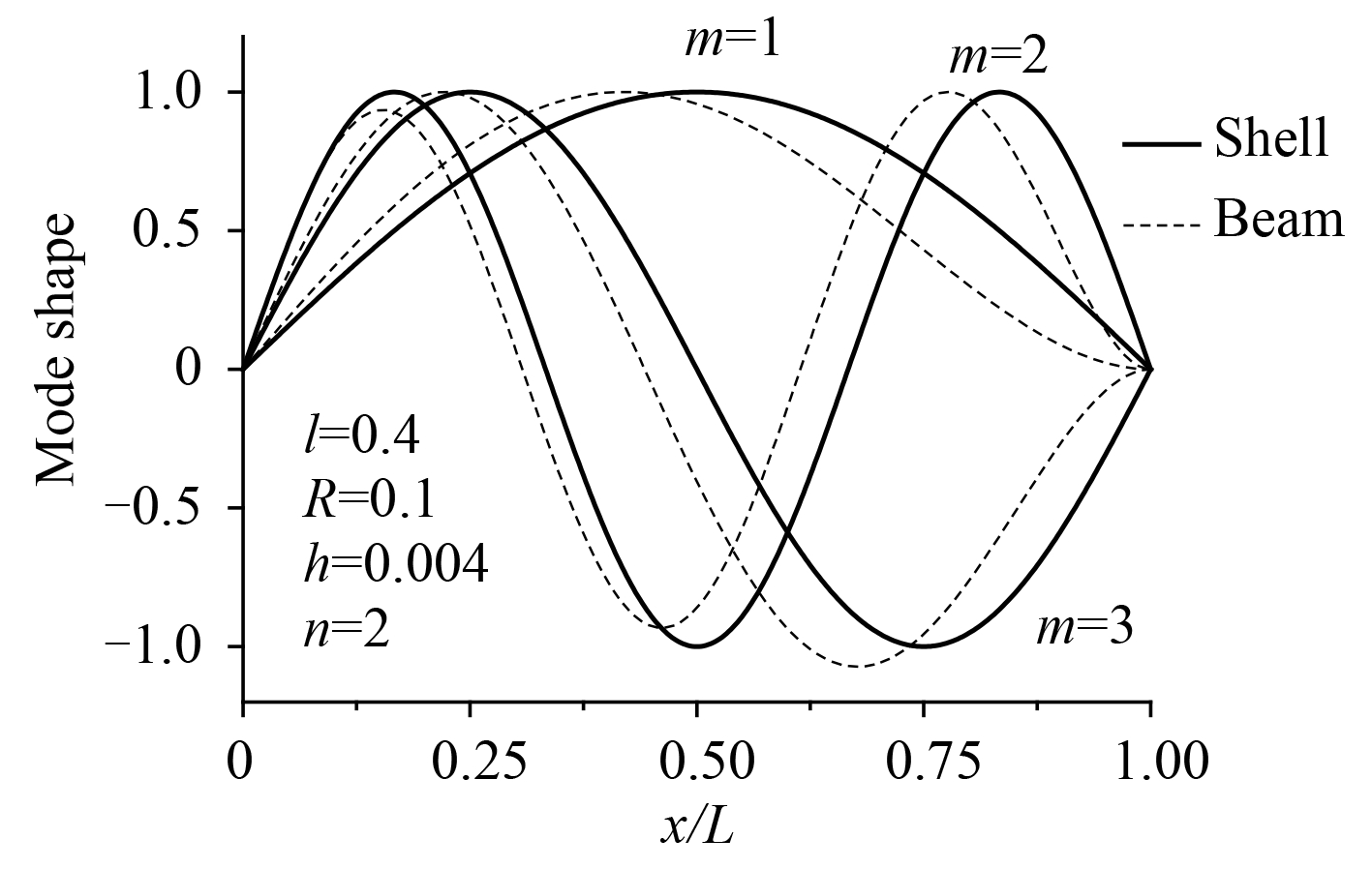
|
图 5 SD-C 边界前 3 阶轴向模态形状 Fig. 5 Axial modes for first 3 modal frequencies for C-SD |
以不同边界下梁的波数节点画水平线和频散图(a)曲线相交,就能够得到圆柱壳的频率,而这也正是波传播法的求解思路。需要注意的是,这种用梁边界代替圆柱壳的边界会带来误差,例如,对于
C-C 边界,类似的结果见图 4。从图 4可以看出,连接梁的波数节点和圆柱壳的频率点的线段已经不平行于横轴。如果用平行线和圆柱壳的(a)分支相交(即波传播方法),则得到的频率就会有较大误差。前 3 阶模态基于梁边界得到的波数
对于
SD-C 边界,前 3 阶频率为 0.148 4,0.346 4 和 0.531 6,对应的纯虚数
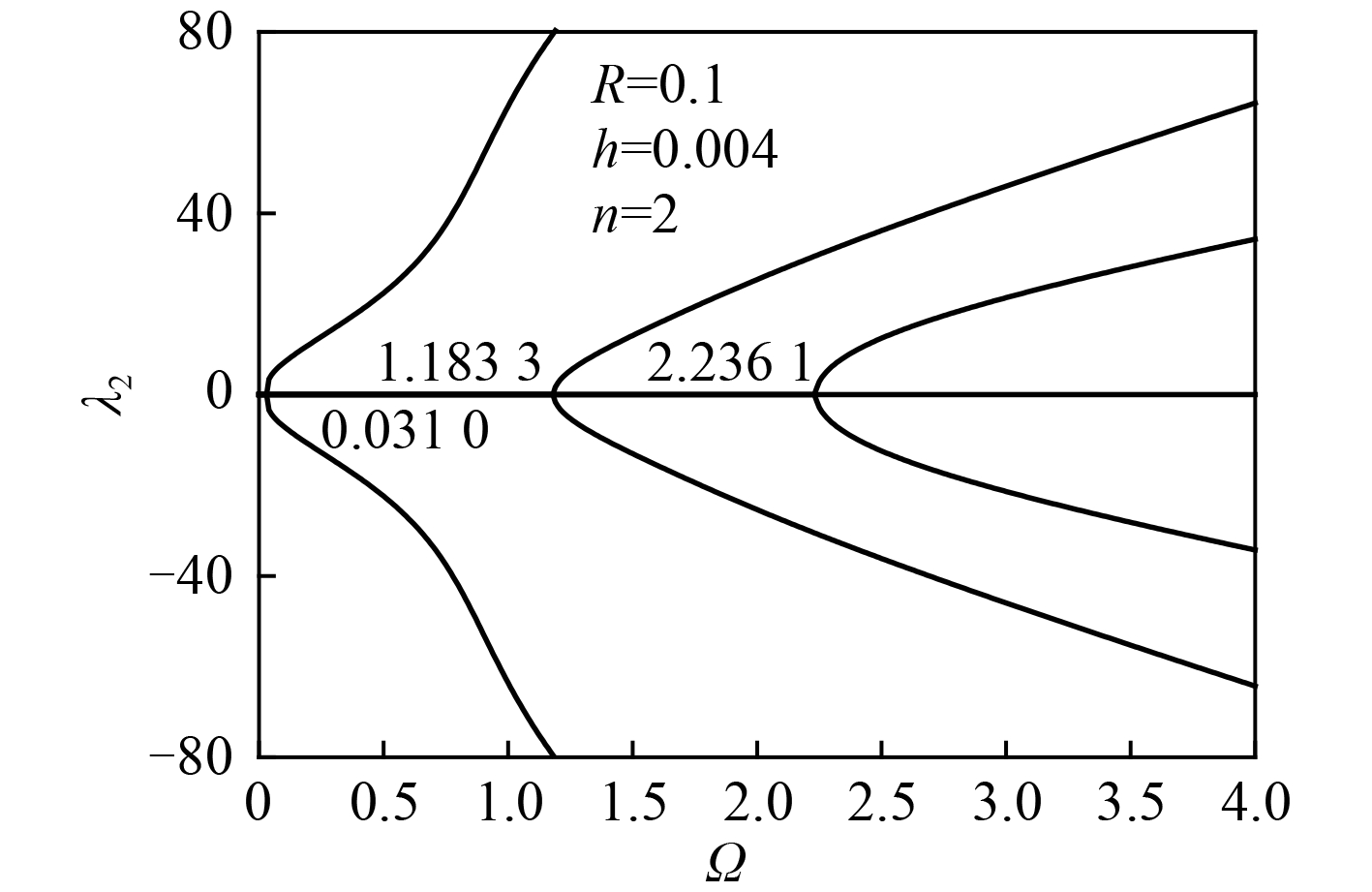
|
图 6 纯虚数解和频率的关系图 Fig. 6 Purely imaginary plot vs frequency parameter |
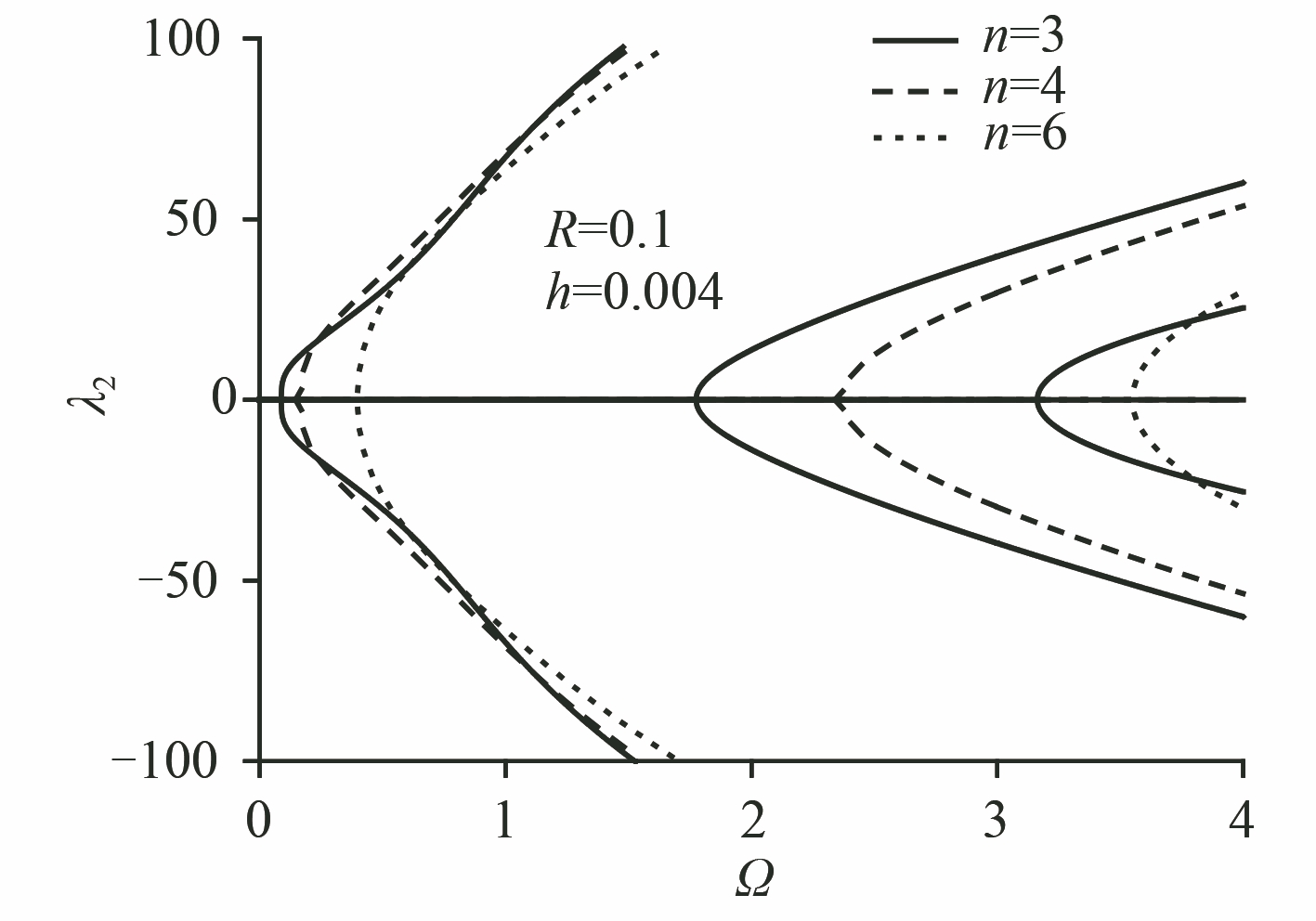
|
图 7 不同 n 值和频率关系曲线 Fig. 7 Purely imaginary plot vs frequency parameter for n = 3, 4, 6 |
图 6给出了纯虚数
λ
2 解随频率变化的情况。根据前述分析,自振频率点位于频散图的纯虚数分支上。对于频率的求解,实际上式(6)在不同的频率区间可以降幂。随着频率逐渐增大,这个方程的次数可以是 2,4 或者 6 次。注意到,图中波数为零时曲线和频率轴有 3 个交点,对于
n = 2,这 3 个频率分别为 0.031 0,1.183 3 和 2.236 1。这 3 个点实际上是圆柱壳中传播波的起始频率
当波数为 0 ,3 个起始频率通过式(8)和式(13)可以得到:
| $\begin{array}{*{20}{l}}\begin{array}{l}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\varOmega _{1,3}^2 = \frac{1}{2}\left( {1 + {n^2} + k{{\left( { - 1 + {n^2}} \right)}^2} \mp } \right.\\[7pt]\left. {\sqrt { - 2k{{\left( { - 1 + {n^2}} \right)}^3} + {k^2}{{\left( { - 1 + {n^2}} \right)}^4} + {{\left( {1 + {n^2}} \right)}^2}} } \right)\text{,} \end{array}\\[7pt]{\varOmega _2^2 = \frac{1}{2}\left( {{n^2} + k{n^2} - {n^2}\nu - k{n^2}\nu } \right)}\text{。} \end{array}$ | (15) |
图 6和图7还可以和长度待定方法联系起来使用。即给定一个频率(大于第 1 个起始频率),总能够找到与之对应的至少 2 个波数 λ(负数舍去),联合边界条件(参考图 3或者图 4),由此波数可以求解得到壳体的长度。这其实就是长度待定方法的求解过程[10],这种方法能够用于圆柱壳的动力设计。
本文是利用系数矩阵行列式进行边界条件的计算并判断频率点。式(12)中 A 是一个复数矩阵。在实际的计算中, A 的行列式并不真正等于 0。通常使用行列式的模值进行频率点的判断。在扫频过程中,模值曲线会出现很多的局部极小值点。对于这些极小点的数值需要仔细甄别。由于起始(截止)频率的存在,低于首个起始频率的点都不会是圆柱壳的自振频率。 图 8给出了一个 SD-SD 边界算例。当 n = 8 时,模值曲线前 2 个极小值点用 P 1 和 P 2 表示,从频散图可以看出, P 1 点对应于 8 个复数解向实数、虚数解和复数解过渡,而 P 2 点就对应首个起始频率, Ω p2 = 0.902 2。从这个过程还可以看出, P 1 和 P 2 点是和圆柱壳的边界条件无关的,它只取决于壳体的几何(不含边界)与材料参数。
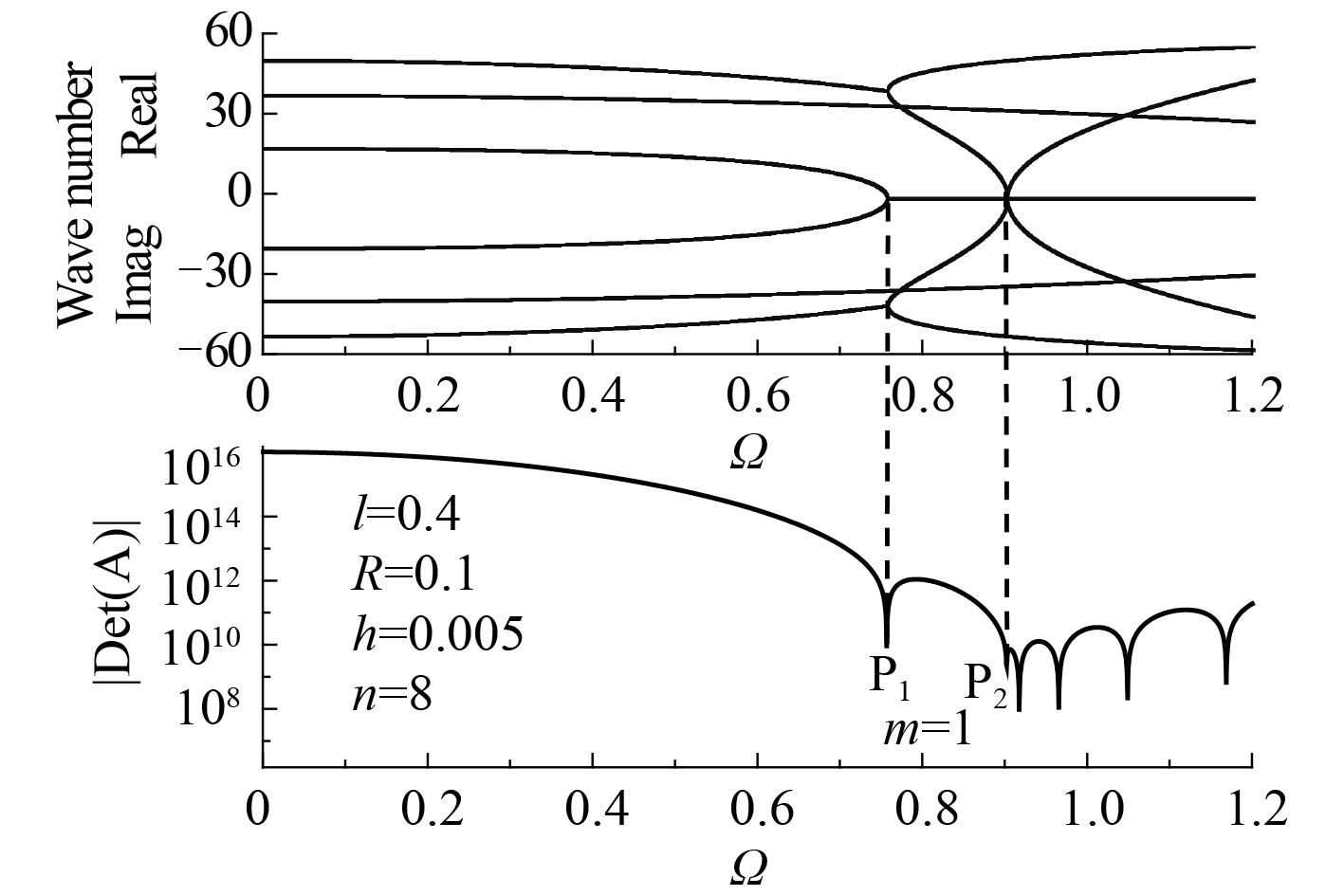
|
图 8 高阶周向波数时的频率求解 Fig. 8 Frequency solution for higher n |

|
图 9 高阶频率计算 Fig. 9 Frequencies for higher modes |
SD-SD 边界的近似梁函数表示中,经常使用三角函数近似表示轴向位移,式(4)就是关于频率 Ω 2 的 3 次方程。根据振型判断,最低频率、中间频率和最高频率分别对应着径向位移分量 w 最大、轴向位移分量 u 最大、切向位移最大 v 而其他 2 个方向位移较小的运动[11]。本文使用的精确解解过程也能够计算对应轴向位移分量 u 和切向位移分量 v 为主的圆柱壳频率。在图 6和图7中,第 2 个和第 3 个起始频率之后的纯虚数分支,就分别代表了轴向位移 u 和切向位移 v 对应的较高频率分布。结合图 3和图 6的思路,可以求解这 2 种较高阶频率。仍旧以 SD-SD 边界为例, 图 9给出了这样的计算过程。从梁的振型结点过来的连接线(平行)对应共有 9 个频率点,这些点反映在系数矩阵行列式曲线上的情况如图 10所示。
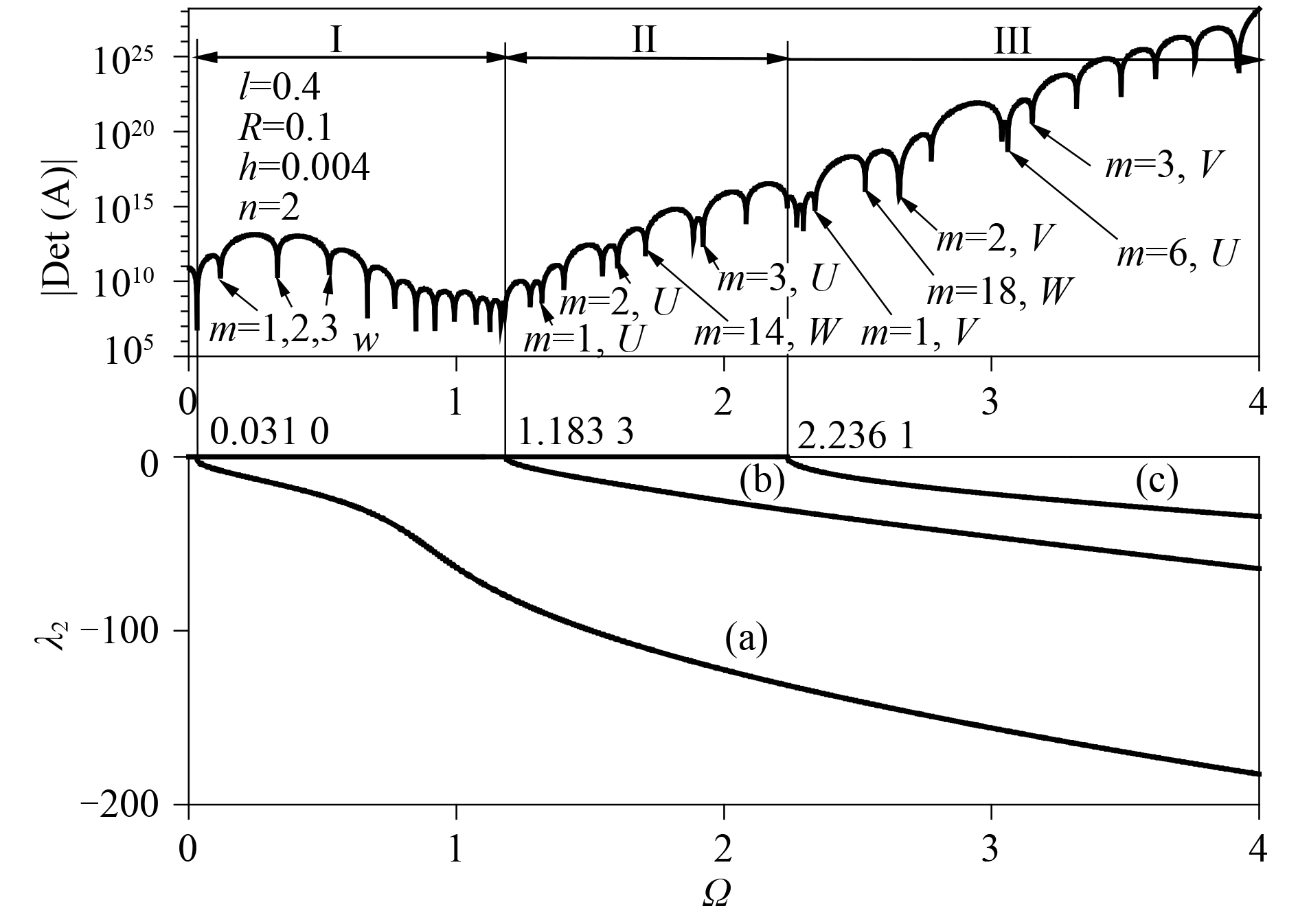
|
图 10 频率区域以及高阶频率求解 Fig. 10 Frequency for axial and tangential modes |
从图 10可看出,第1阶起始频率为 0.031,远小于环频率( Ω ring = 1)。在 [0.031,1] 频率区间有很多的频率点,它们对应于径向 w 为主的振型。轴向位移 u 为主的频率出现在第 2 个起始频率之后,切向位移 v 为主的频率则出现在第 3 个起始频率之后。图中依照起始频率给出了 3 个频率范围(Ⅰ 区, Ⅱ 区和 Ⅲ 区)。在 Ⅰ 区只有( a)分支,即这个区域内的振动均是对应径向位移较大的情况,这也就是通常圆柱壳振动考虑的范围( Ω<1)。在区域 Ⅱ 内,存在 2 条曲线( a)和( b),因此,会出现轴向位移 u 比较大的振型(曲线( b)),如 m = 1,2,3 的轴向振型,也会出现高阶对应径向位移 w 为主的振型(曲线(a)),例如 m = 14 时,对应的 3 个频率是 1.707 2,6.616 6 和 11.181 3。在 Ⅲ 区域里,则 3 种振型会并存。图中除了给出切向 v 为主的前3阶频率点,也给出了 m = 18 时径向振动为主以及 m = 6 时轴向振动为主的频率点。
为了更好理解频散图形对于求解频率的理解,本文还给出了方程(4)的三维图形。从图中能够清晰看出 8 个波数随频率的变化情况。
3 结 语本文采用精确解方法研究圆柱壳的自由振动频率特性。可以得到如下结论:
1)圆柱壳的所有齐次边界条件的频率点都存在于频散曲线中的纯虚数分支上。对于振动而言,根据研究的频率范围,频散曲线可以退化为 2,4 或者 6 次方程。
2)精确解方法能够求解对应的以轴向位移和切向位移为主的频率,它们和高阶径向为主的频率交叉在一起。
3)圆柱壳自振存在着最低的起始频率,这个频率点对应于无限长圆柱壳的频率。加上边界约束之后的频率均高于该起始频率。
4)通常采用的梁横向振动振型和波传播法得到的频率均存在误差。其中 SD-SD 的误差非常小,可以忽略。边界约束越强,壳体越短,则误差越大。
| [1] | LEISSA A W. Vibration of Shells (NASA SP 288)[R]., 1993. |
| [2] | FORSBERG K. Influence of boundary conditions on the modal characteristics of thin cylindrical shells[Z]. 1964: 2. |
| [3] | Dai L, Yang T, Du J, et al. An exact series solution for the vibration analysis of cylindrical shells with arbitrary boundary conditions[J]. Applied Acoustics, 2013, 74 : 440–449. DOI: 10.1016/j.apacoust.2012.09.001 |
| [4] | Sharma C B. Free vibrations of clamped-free circular cylinders[J]. Thin-Walled Structures, 1984, 2 (1): 175–193. |
| [5] | FLUGGE. Stresses in shells[M]. Springer: 1973. |
| [6] | Zhang X M, Liu G R, Lam K Y. Vibration Analysis Of Thin Cylindrical Shells Using Wave Propagation Approach[J]. Journal of Sound and Vibration, 2001, 239 (3): 397–403. DOI: 10.1006/jsvi.2000.3139 |
| [7] | Xuebin L. Study on free vibration analysis of circular cylindrical shells using wave propagation[J]. Journal of Sound and Vibration, 2008, 311 : 667–682. DOI: 10.1016/j.jsv.2007.09.023 |
| [8] | 方同, 薛璞. 振动理论及应用[M]. 西安: 西北工业大学出版社, 1998. |
| [9] |
陈正翔, 江松青, 张维衡. 圆柱壳中结构振动波的传播特性[J]. 振动工程学报, 1998, 11 (4): 450–456.
Chen Zhengxiang, Jiang Songqing, Zhang Weiheng. Dispersion Characteristics of Structure Vibration Waves in Cylindrical Shells[J]. Journal of Vibration Engineering, 1998, 11 (4): 450–456. |
| [10] | WARBURTON G B. Vibration of thin cylindrical shells[Z]. 1965: 7, 399–407. |
| [11] | ARNOLD R N, WARBURTION G B. Flexural vibrations of the walls of thin cylindrical shells having freely supported ends[Z]. 1949: 197. |
 2017, Vol. 39
2017, Vol. 39
