2. 哈尔滨工程大学船舶工程学院,黑龙江 哈尔滨 150001;
3. 青岛海西重机有限责任公司,山东 青岛 266000
2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China;
3. Qingdao Haixi Heavy-duty Machinery Co., Ltd., Qingdao 266000, China
船舶在航行时,遇到恶劣海况,常常会产生剧烈的摇荡运动,导致波浪与船体之间发生剧烈的冲撞现象,这种现象称为砰击。砰击导致的破坏后果严重,不仅能损伤局部结构,而且能使全船的强度丧失。为了避免双体船受砰击而导致局部结构损伤乃至失效,因此,寻找一种适合双体船的砰击载荷计算方法,仍然具有很重要的现实意义。
Von Karman[1]最早开始研究楔形体结构入水问题,忽略液面升高的影响和流畅运动对结构的冲击,提出了砰击压力公式;Jason John McVicar等[2]基于模态法,研究了砰击时间和砰击力的瞬时形态对双体船的影响;戴仰山等[3]探讨了底部砰击响应对于船体总纵强度的影响;于鹏垚等[4]研究了船首外飘砰击设计载荷直接计算;夏齐强等[5]针对双体船湿甲板砰击和连接桥易受到砰击的特点,分析了迎浪状态时,在波浪载荷与砰击载荷共同作用下小水线面双体船的结构响应,并研究了砰击载荷对结构强度的重要影响;刘佳[6]通过Ls-Dyna显示非线性动力分析软件,模拟分析不对称双体船在砰击作用下不同部位所受到的压力、应力响应与运动响应;岳永威等[7]利用Ansys建立双体船有限元模型,采用冲击波压力算法,在时域中对双体船的薄弱部位和典型部位进行强度分析。然而双体船的这种砰击模式是船体与波浪相互作用而产生的一种高度非线性现象,在船体入水过程中,船体、空气和水进行了复杂的耦合作用,特别是空气层在船体入水过程中的“活塞压缩”情况对湿甲板砰击压力的峰值和分布情况造成了很大的影响。若严格进行求解,问题将会非常复杂,且计算量庞大。总的来说,对双体船砰击载荷的研究尚显欠缺,需要对此问题进行一些近似和假设,从而提出一套较为经济可行的工程实用方法。
本文借助CCS指南[8],研究校核大型SWATH船局部砰击强度的规范计算。并通过直接计算的方法,求解得到船在不规则波中的相对位移时历,进而求得相对速度时历,得到砰击时刻并求的船首附近剖面的砰击压力,研究砰击计算结果的差异,为相关船型的砰击载荷预报和结构优化提供了参考。
1 砰击载荷规范计算及强度评估 1.1 有限元模型结合CCS《小水线面双体船指南》有关规定和双体船的结构特性,通过通用的有限元软件MSC.PATRAN建立全船有限元模型。模型如图 1所示。

|
图 1 全船有限元模型 Fig. 1 The finite element model of whole ship |
波浪砰击压力的大小、作用位置和区域随时间变化。其瞬时峰值对面板和局部扶强材的作用影响尤为显著。在合理选取净空后,砰击压力峰值
| ${{{P}}_{{\rm{max}}}} = {{n}}{{{L}}_{{P}}}{\left( {{{{L}}_{{b}}}} \right)^{{\rm{1}}.0{\rm{8}}}}{\rm{kN}}/{{\rm{m}}^{\rm{2}}}{\text{,}}$ | (1) |
式中:
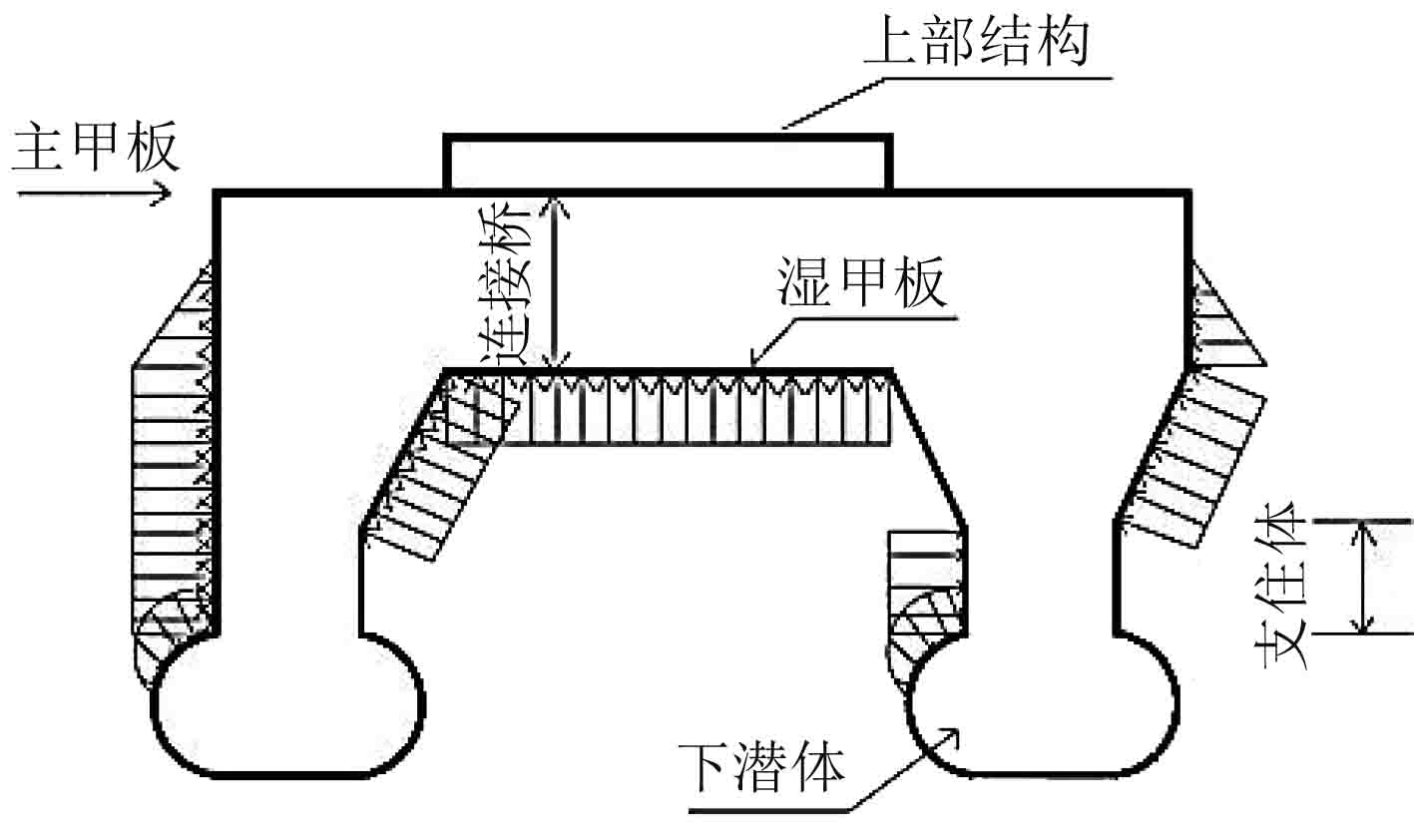
|
图 2 砰击压力分布 Fig. 2 Slamming pressure distribution |
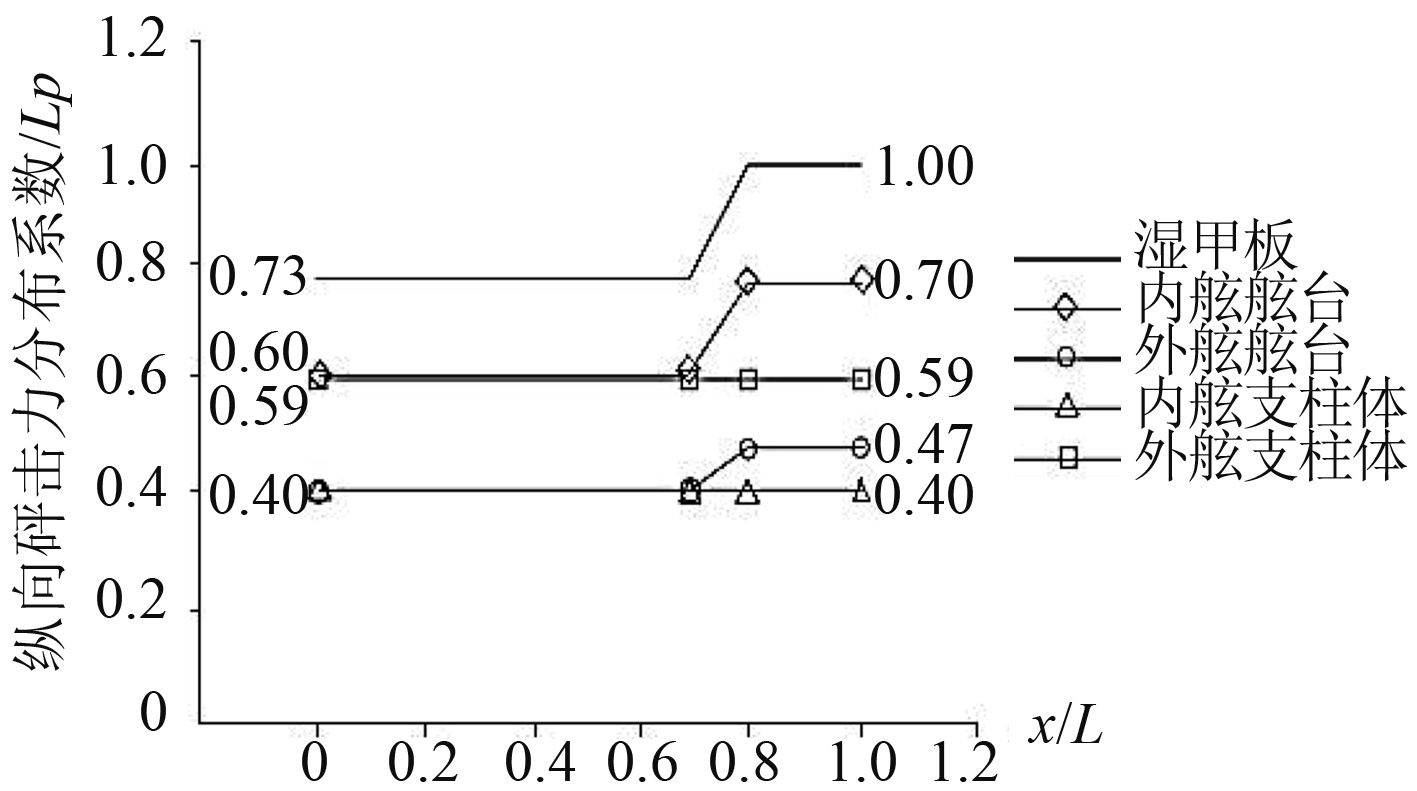
|
图 3 纵向砰击力系数 Fig. 3 Longitudinal slamming force coefficient |
当砰击现象发展到较大区域时,可表征为板格或板架整个作用区域上的平均垂向设计压力
| ${{{P}}_{{{des}}}} = {{{P}}_{{\rm{max}}}}\left[ {{{{K}}_{{d}}}/{{{K}}_{{n}}}} \right]{\rm{ kN}}/{{\rm{m}}^{\rm{2}}}\text{,}$ | (2) |
式中
| ${K_d} \!=\! \left\{\!\! \begin{array}{l}1, {\text{当}}{A_d}/{A_r} \leqslant 0.000\,\,25\text{;}\\[5pt]0.277\,\,6 + 0.015\,\,4{[ - {\log _{10}}({A_d}/{A_r})]^3}\text{,}\\[5pt]\text{当}0.000\,\,25 \leqslant {A_d}/{A_r} \leqslant 0.022\,\,6\text{;}\quad\quad\quad\quad\quad\quad\quad\!\!(3)\\[5pt]0.09 \!+\! 0.37{[\! - {\log _{10}}({A_d}/{A_r})]^{1.5}}, {\text{当}}0.022\,\,6 \!\leqslant\! {A_d}\! /\!{A_r} \!\!\leqslant \!\! 1n\text{。}\end{array} \right.$ |
式中: K n 为系数,计算同 K d ,但计算时取 A d 为 1 m 2; A d 为 P des 的作用覆盖面积,取与 A r 同一单位; A r 为参照面积,m 2,且按下式计算:
| ${{{A}}_{\rm{r}}}=0.0{\rm{6}}{{{L}}_{{b}}}{{B}}{\text{。}}$ | (4) |
式中:
由于计算的是湿甲板处的砰击,本次计算加载位置选取为水线以上至 z 方向 14 m处全船外壳部分。如图 4所示。

|
图 4 全船砰击载荷加载 Fig. 4 The action position of ship slamming load |
砰击加载根据公式将全船分为 12 个部分,以水密舱壁进行划分。从船尾至船首分段位置如表 1所示。
|
|
表 1 分段位置表 Tab.1 Hull section position |
采用MSC.PATRAN及其PCL场函数功能实现砰击压力的有限元加载计算。部分结构应力响应云图如图 5~ 图 6所示。

|
图 5 舷台横框架应力云图 Fig. 5 Stress calculation of sponson transverse frame |

|
图 6 湿甲板应力云图 Fig. 6 Stress calculation of wet deck |
选取部分船体构件并提取结果,结果如表 2所示。
|
|
表 2 规范计算最大Mises应力计算结果 Tab.2 The maximum Mises stress calculation result of specification |
由应力云图可看出,高应力结果集中在船首区域,但在舷台及支柱体也存在高应力区域。且高应力区域基本在横纵构件上,湿甲板应力较小。由表格看出,砰击对大型SWATH船中的一些结构强度影响很大,横舱壁、横框架、外板的应力水平均较大,纵向构件例如纵舱壁、纵隔板、纵桁影响尤其较大,大型SWATH船的纵向强度受砰击影响较大,而且这种影响是不能忽视的,需要重点关注。
2 砰击载荷直接计算及强度评估 2.1 概述该部分基于三维线性势流理论,对船体与波浪之间的相对速度进行直接计算,选取强度评估中最可能发生砰击的工况,结合经验公式确定砰击压力系数,预报典型剖面的砰击压力,实现砰击载荷的直接计算。通过对船体进行有限元强度分析,计算得到全船的应力分布,并与规范计算结果进行比较分析。
2.2 砰击发生的条件湿甲板砰击情况在船舶寿命期内并不时有发生,需要满足一定的运动条件。首先,湿甲板与波浪接触是发生砰击的必要条件,否则砰击现象将无法产生。此外,理论与试验研究都表明,当平板发生砰击时,只有当垂向相对速度超过了某一阀值时,才会在结构上产生可以计量的压力值。因此,当船体的相对运动满足以上 2 个条件时,认为湿甲板砰击情况发生。
设纵摇角为
| ${{{Z}}_{{R}}} = {{{Z}}_{{G}}} - {\rm{x}}{{\rm{\theta }}_{\rm{y}}} - {\rm{\zeta }}{\text{,}}$ | (5) |
砰击的发生,涉及的是船舶与波浪在空间的相对位置,因此,这时的垂向相对速度应为上式对时间的求导:
| ${{{\dot Z}}_{{R}}} = {{{\dot Z}}_{{G}}} - {\rm{x}}{{\rm{\dot \theta }}_{\rm{y}}} - {\rm{\dot \zeta }}{\text{,}}$ | (6) |
发生砰击时,相对运动为负,所以需要满足:
| ${Z_R} \leqslant - {\dot Z_R}{\text{。}}$ | (7) |
船在满载状态下吃水为 7.5 m,湿甲板距离基线的高度为 11 m,则只需保证波面与湿甲板的相对位移为 3.5 m即可,且同时保证二者的相对速度为负。
2.3 砰击压力的计算借助劳式船级社规范[9]计算连接桥处砰击压力,公式为
| $P = \frac{1}{2}{{\rm{k}}_{s1}}{V_{bs}}^2\;{\rm kN/{m^2}}{\text{,}}$ | (8) |
式中
| ${{{k}}_{s1}} = \frac{\pi }{{\tan {\beta _p}}},\text{当}{\beta _p} \geqslant 10\text{时;}$ | (9) |
| ${{{k}}_{s1}} = {\rm{28}}\left( {{\rm{1}} - \tan \left( {2{\beta _p}} \right)} \right),\text{当}{\beta _p} < 10\text{时。}$ | (10) |
式中:
可以看出,砰击压力主要由砰击压力系数和冲击速率决定,而砰击压力系数仅取决于砰击角,根据连接桥发生砰击区域的特点,取砰击角为 0°。
2.4 相对运动时历计算对于该双体船,航速取为 5 kn,有义波高参考海浪谱响应海况有义波高的平均值,跨零周期的确定首先需估计船本身的对应特征周期,该双体船在 8.5 s左右,跨零周期选取接近船的特征周期的值。取 6 级海况,取波浪的
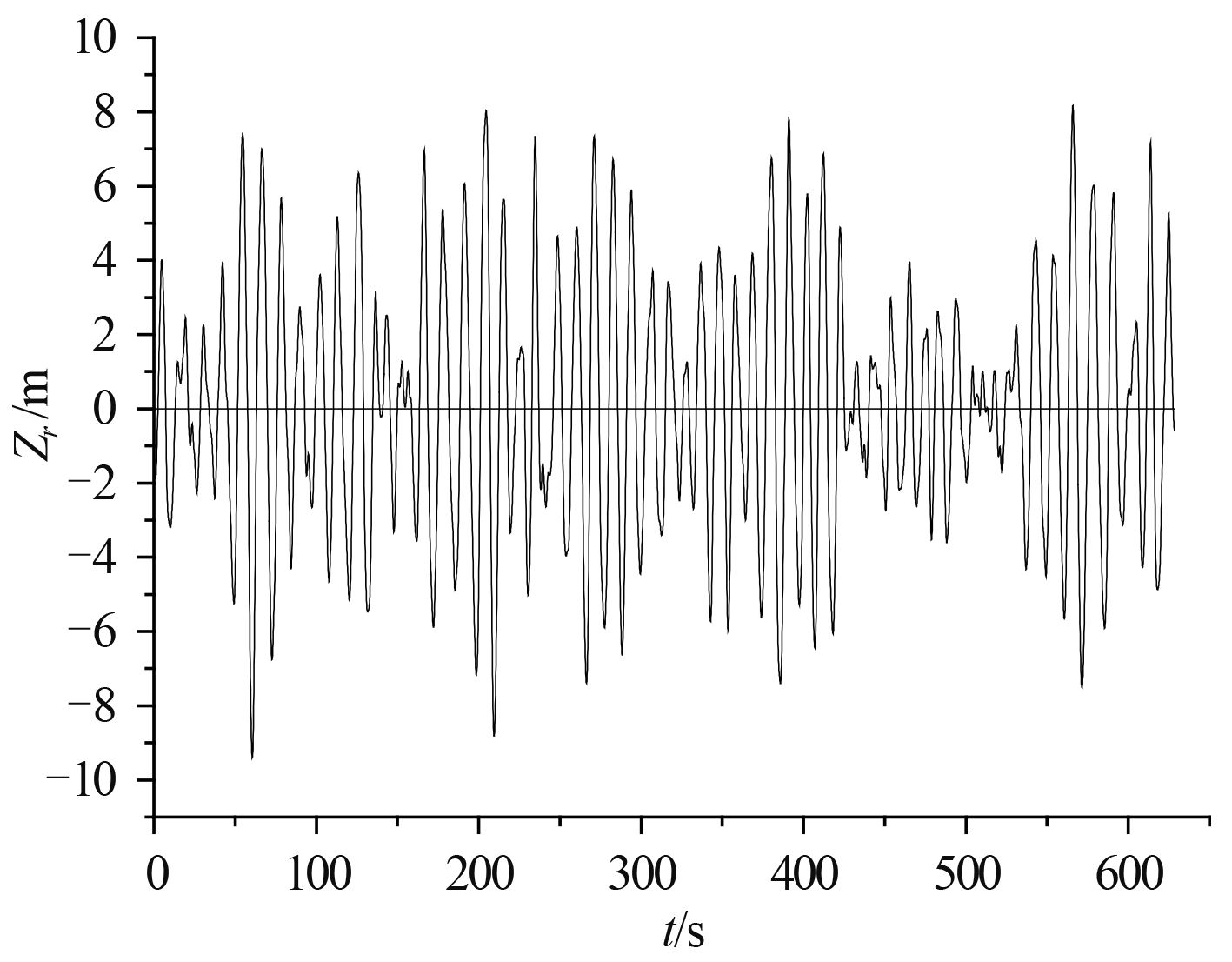
|
图 7 6 级海况相对位移时历 Fig. 7 Relative displacement time-history of level 6 sea condition |

|
图 8 6 级海浪相对速度时历 Fig. 8 Relative velocity time-history of level 6 sea condition |
依照砰击载荷规范计算的载荷加载方式,将上述剖面的砰击压力加载到相应部位,得到计算结果。部分结构应力响应云图部分如图 9~ 图 10所示。

|
图 9 舷台横框架应力云图 Fig. 9 Stress calculation of sponson transverse frame |

|
图 10 湿甲板应力云图 Fig. 10 Stress calculation of wet deck |
选取部分船体构件并提取结果,结果如表 3所示。
|
|
表 3 直接计算最大Mises应力计算结果 Tab.3 The maximum Mises stress calculation result of direct calculation |
计算得到各个部位的应力大小,可以看出在船首附近发生砰击时,对 2 个部位的影响较大,即舷台及支柱体处在FR168 处的横框架,尤其在距离中部 6.72 m附近,应力值达到 299 MPa,另一处为隔板,位于FR168 处的横隔板应力值达到 300 Mpa,FR164-FR172 处的纵隔板应力达到 573 MPa,而湿甲板的应力值也较规范计算的大,达到 163 MPa。
2.6 计算结果比较分析将规范计算砰击响应、直接计算砰击响应进行比较分析,所得结果如表 4所示。
|
|
表 4 砰击载荷最大Mises应力计算结果对比 Tab.4 The maximum Mises stress calculation results compared of slamming load |
由计算结果可知规范加载下,上建围壁、上船体横舱壁、隔板、舷台支柱横框架、舷台支柱纵桁较为危险。直接计算下砰击载荷对上船体横舱壁、隔板、舷台及支柱体横框架的影响较大,尤其在船首肋位号FR168-FR172 的结构强度需要重点考虑,二者在上述结构能保持相对的一致性。然而双体船砰击模式与常规的平板入水砰击模式毕竟不同,湿甲板并不是同时全面地进入水中,存在时间和空间上的分布不均匀性,且涉及到流体,空气和结构的动态耦合分析,规范计算的经验公式仍存在着部分局限性。在某些少数部位,例如湿甲板、隔板、舷台及支柱体横框架,直接值较规范值大,反映了直接计算在特殊部位更有准确性、合理性。
3 结 语本文通过使用 2 种不同的砰击载荷的计算方法,对比分析了砰击载荷对双体船强度的影响,得出了以下结论:
1)综合规范校核与直接计算的结果来看,规范校核比直接计算更为保守,影响的区域更广;
2)对于双体船,湿甲板的砰击是需要予以足够的重视,由上述对比结果可发现,直接计算的计算结果与规范结果相比较大,这与实际情况比较相符,可以发现直接计算较规范计算在某些特殊结构处更具有针对性,结果更为合理;
3)砰击对强度有一定影响,比较 2 种砰击载荷的计算方法发现,应当对船首附近的隔板结构、船体横框架以及湿甲板进行重点关注,为以后双体船结构优化设计提供了依据。
| [1] | VON KARMAN T. The impact on seaplane floats during landing. NACA TN321, Oct. 1929. |
| [2] | Thomas G, Winkler S, Davis M, et al. Slam events of high-speed catamarans in irregular waves[J]. Journal of Marine Science & Technology, 2011, 16 (1): 8–21. |
| [3] |
戴仰山, 贺五洲. 底部砰击预报[J]. 中国造船, 1979 (2): 37–48.
Dai Yangshan, He Wuzhou. The bottom slamming prediction[J]. Journal of China shipbuilding, 1979 (2): 37–48. |
| [4] | 于鹏垚, 任慧龙, 李陈峰, 刘亚冲, 等. 船首外飘砰击设计载荷直接计算[J]. 船舶力学, 2016, 12 : 566–573. DOI: 10.3969/j.issn.1007-7294.2016.05.007 |
| [5] | 夏齐强, 陈志坚. 波浪载荷与砰击载荷联合作用下SWATH船结构动态响应[J]. 上海交通大学学报, 2012 (03). DOI: 10.3969/J.ISSN.1671-9964.2012.03.003 |
| [6] | 刘佳. 不对称双体船在规则波中砰击过程的数值仿真[D]. 大连: 大连理工大学, 2010. |
| [7] |
岳永威, 王超, 方超, 等. 军用双体船抗冲击特性数值研究[J]. 中国舰船研究, 2012, 07 (1): 29–34.
Yue Yongwei, Wang Chao, Fang Chao, et al. Numerical studies military catamaran shock characteristics[J]. Chinese ships research, 2012, 07 (1): 29–34. |
| [8] | 中国船级社. 小水线面双体船指南. 2005: 6–45. |
| [9] | 英国劳氏船级社. 海军舰艇入级规范通则[S]. 2011. |
 2017, Vol. 39
2017, Vol. 39
