0 引　言

近年来，近场声全息技术^{[1 –2]}（NAH）在噪声识别与定位、振动和声辐射特性研究等领域发展迅速，尤其是 Williams等^[3]在 20 世纪 80 年代初提出的基于 FFT 的平面 NAH 技术，因其理论简单，测量方便，易于计算和分析，在工程实际中应用广泛。

在应用平面 NAH 技术进行声场重建时，由于背景噪声分布在整个波数域范围内，逆向重构时位于高波数区域内的背景噪声将会被急剧放大，导致全息重构结果出现较大误差。因此，需要对全息面复声压数据进行波数域滤波^[4]。目前常用的滤波窗函数主要有维纳（Wiener）滤波窗^[5]以及带约束条件的最小二乘滤波窗^[6]。在上述 2 种窗函数中，信噪比都是重要参数，能够直接决定滤波截止波数的选定，严重影响波数域滤波和声场全息重构效果。

但是，信噪比无法在测量过程中直接得到，需要根据全息面测量数据进行估计。辛雨等^[7]提出以辐射圆外的波数域成分数据的均方根值近似代替全息面的噪声信号均方根值，采用能量法进行信噪比估计，但其估值严重依赖全息面数据的选取，而且无法判定估值是否准确。本文在其研究基础上给出波数域内的信噪比估值公式，提出一种判别估值是否精确的方法，并指出可以减小全息面采样间隔来降低估值误差。本文以 2 个点声源为例进行仿真，给出在不同采样间隔下满足不同误差条件的最大信噪比估值，可作为实际应用中的参考。

1 平面 NAH 基本原理^[8]

设全息面测量得到的复声压数据为 ${p_H}(x,y,{z_H})$ ，则有：

$\begin{split}\\[-12pt]{P_H}(x,y,{z_H}) = & \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {{P_s}({{x',y',}}{{{z}}_s})} } {g_D}\times\\[8pt]& {{(x - x',y - y',}}{{{z}}_H}{\rm{ - }}{{{z}}_s}{{){\rm d}x'{\rm d}y'}}{\text{，}}\end{split}$

(1)

式中： ${P_s}(x',y',{Z_s})$ 为声源面声压； ${g_D}(x,y,z)$ 为 Dirichlet 边界条件下的格林函数。

${g_D}(x,y,z) = \frac{{z(1 - ikr)}}{{2\pi {r^3}}}{\text{，}}$

(2)

式中， $r = \sqrt {{x^2} + {y^2} + {z^2}} $ ； $k = \omega /c = 2\pi /\lambda $ 为波数； $\omega $ 为声波的角频率； $\lambda $ 为特征波长。

定义二维傅里叶变换为：

$F({k_x},{k_y}) = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {f(x,y){e^{ - i({k_x}x + {k_y}y)}}{\rm d}} } x{\rm d}y\text{，}$

(3)

对式（1）两边取二维傅里叶变换，并由卷积定理可得：

${P_H}({k_x},{k_y},{z_H}) = {P_S}({k_x},{k_y},{z_S}){G_D}({k_x},{k_y},{z_H} - {z_S})\text{，}$

(4)

式中 ${G_D}({k_x},{k_y},z)$ 为 ${g_D}(x,y,z)$ 的二维傅里叶变换。其表达式为：

${G_D}({k_x},{k_y},z) = {e^{i{k_z}z}}\text{，}$

(5)

当 $k_x^2 + k_y^2 \leqslant {k^2}$ 时，

${k_z} = \sqrt {{k^2} - (k_x^2 + k_y^2)}\text{；} $

(6)

当 $k_x^2 + k_y^2 > {k^2}$ 时，

${k_z} = i\sqrt {(k_x^2 + k_y^2) - {k^2}}\text{，} $

(7)

式中 ${k_x},{k_y}$ 分别对应x、y 方向的空间波数。

将式（5）代入式（4），可得：

${P_H}({k_x},{k_y},{z_H}) = {P_S}({k_x},{k_y},{z_S}){e^{i{k_z}({z_H} - {z_S})}}\text{。}$

(8)

由式（8），已知 $z = {z_s}$ 平面的声压数据时可以预测出 $z = {z_H} > {z_S}$ 的声压情况，并进一步获得其他声场量；同样，已知 $z = {z_H}$ （全息面）的声压数据也可以反演更近的表面 $z = {z_S}$ （重建面）的声压数据及其他声学量。重建公式如下：

${P_S}({k_x},{k_y},{z_S}) = {P_H}({k_x},{k_y},{z_H}){e^{ - i{k_z}({z_H} - {z_S})}}\text{。}$

(9)

2 信噪比定义与噪声能量计算

信噪比即 SNR（Signal to Noise Ratio）是指信号中有用信号和噪声信号的比值，其大小通常用分贝数表示。信噪比可以使用信号或噪声的有效功率或能量定义，也可以使用信号和噪声声压的幅值定义。本文使用能量定义信噪比，公式为：

$SNR = 10\lg \frac{{{E_S}}}{{{E_N}}}{\rm{ = }}10\lg \frac{{E - {E_N}}}{{{E_N}}}\text{。}$

(10)

式中：E_S 和E_N 分别为全息面信号和噪声的能量；E 为全息面总能量。

由式（10）可知，只要获得全息面噪声信号的能量，就可以估计出全息面信噪比。记全息面实际测量声压信号为 $p(x,y,{z_H})$ ，噪声信号为 ${p_N}(x,y,{z_H})$ ，且噪声信号为平稳随机分布，其均值为 0。M，N 分别为全息面上x，y 方向的总测量点数， $E\left[ \bullet \right]$ ， $D\left[ \bullet \right]$ 分别表示数学期望和方差，有

$\left\{ \begin{array}{l}E[{p_N}(x,y,{z_H})] = \displaystyle\frac{1}{{MN}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{p_N}({x_i},{y_j}) = 0{\text{，}}} } \\[5pt]D[{p_N}(x,y,{z_H})] = \displaystyle\frac{1}{{MN}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {\{ {p_N}({x_i},{y_j}) - } } \\[5pt]\quad \quad E[{p_N}(x,y,{z_H})]{\} ^2} \!\!=\!\! \displaystyle\frac{1}{{MN}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{p_N}{{({x_i},{y_j})}^2{\text{。}}}} } \end{array} \right.$

(11)

由式（11）可得：

${E_N} = MND[{p_N}(x,y,{z_H})]\text{。}$

(12)

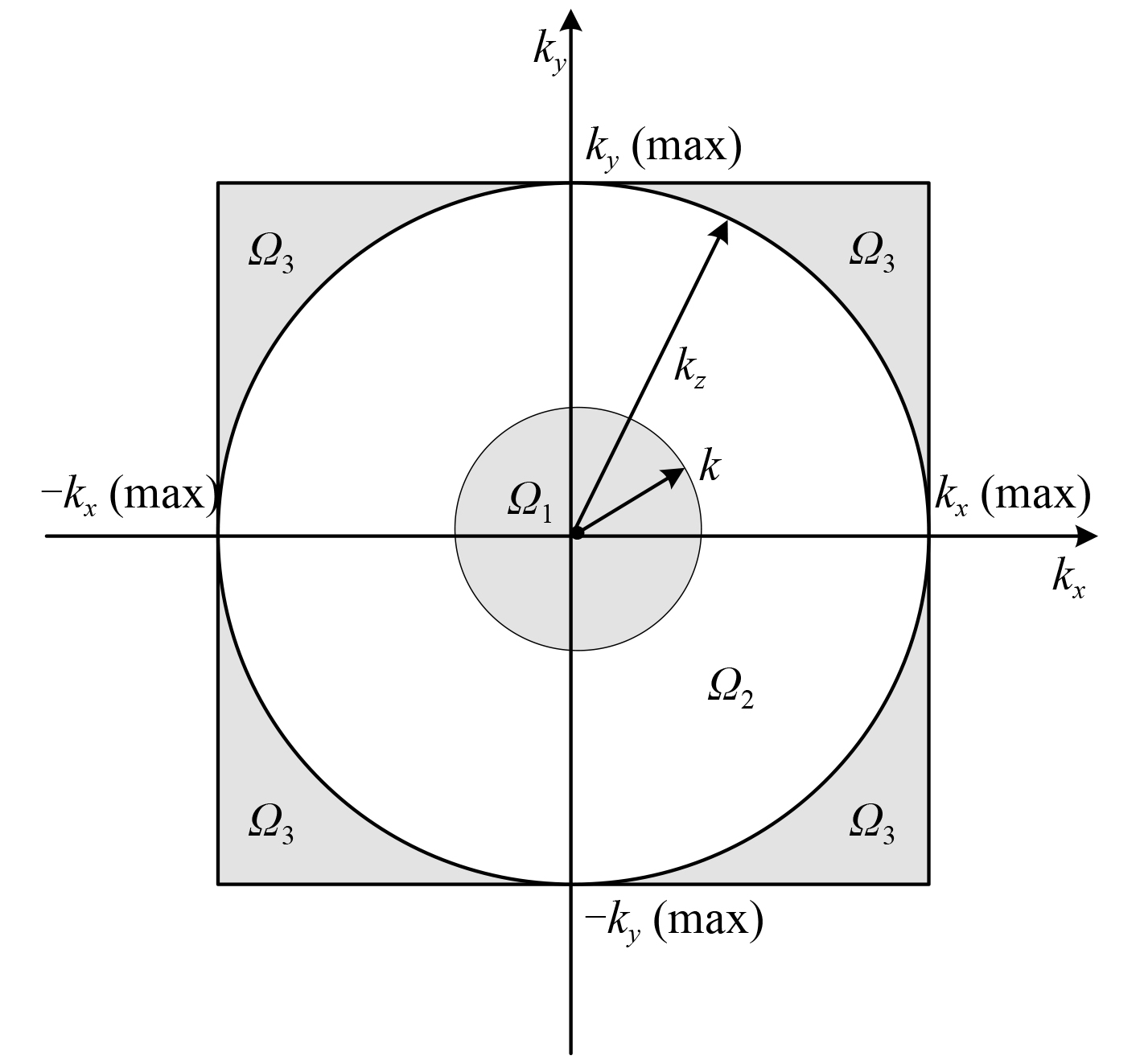
式（12）本质上是噪声信号在空间域内的能量计算公式，只要估算出噪声信号在空间域内的方差，就可以估计出全息面内噪声的能量。但是全息面记录的声压信号是理论声压信号和噪声信号的混合，无法将噪声信号分离出来估计其方差。所以需要在波数域中进行讨论。根据采样定理可知，波数 ${k_x}(\max ) = \pi /\Delta x$ ， ${k_y}(\max ) = \pi /\Delta y$ ，记 ${k_r} = \sqrt {k_x^2 + k_y^2} $ ，将波数域划分为 3 个区域，如图 1 所示。

其中 ${\varOmega _1}$ 对应 ${k_r} < k$ 的波数区域，即辐射圆以内的波数成分，记G_D 为重建面到全息面的传递算子，则 ${\varOmega _1}$ 区域内G_D 幅值恒为 1，对应在传播过程中幅值不随距离衰减的“平面波”，该区域通常包含较大能量； ${\varOmega _2}$ 区域对应 ${k_r} < k < {k_{\max }}$ 的波数成分，此时G_D 为一负指数函数，对应在传播过程中幅值随距离衰减的“倏逝波”； ${\varOmega _3}$ 区域对应 ${k_{\max }} < {k_r}$ 的波数成分，同样为“倏逝波”，而且具有更高的波数成分，在传播过程中衰减的更为迅速。一般而言， ${\varOmega _3}$ 区域内的声压信号几乎全被噪声信号所淹没，无法再应用于重构，因此可以利用 ${\varOmega _3}$ 区域内的波数成分估计全息面噪声信号的能量。

考虑到噪声信号在空间域内是平稳随机分布的，则其在波数域内也必然是平稳随机分布的，因此全息面噪声信号在整个波数域内的方差可以用 ${\varOmega _3}$ 区域内的方差近似估计。即

$\begin{split}\\[-12pt]D[{P_N}({k_x},{k_y},{z_H})] = \frac{1}{{MN}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {} }\text{，} \\{p_N}{({k_x}_i,{k_{yj}},{z_H})^2} \approx D[{P_N}({\Omega _3})]\end{split}\text{。}$

(13)

式中： ${P_N}({k_x},{k_y},{z_H})$ 为 ${p_N}(x,y,{z_H})$ 的二维傅里叶变换； ${P_N}({\varOmega _3})$ 为全息面声压角谱中位于 ${\varOmega _3}$ 区域内的波数成分。而由 Parseval（巴塞伐）定理知，噪声信号在空间域中的总能量等于其波数域内的总能量，即

$ {E_N}\!\!\! =\!\!\! \sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{p_N}{{({x_i},{y_j})}^2}} }\!\!\! =\!\!\! \frac{1}{{MN}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{p_N}{{({k_x}_i,{k_{yj}},{z_H})}^2}} }\text{，} \!\!\!\! $

(14)

式中 ${\left\| \bullet \right\|_2}$ 为矩阵的 2–范数；b 为 ${\varOmega _3}$ 区域内的总测量点数。由式（13）和式（14）可知，全息面中噪声信号的总能量E_N 可以估计为：

${E_N} \approx D[{P_N}({\varOmega _3})] = \frac{1}{b}{({\left\| {{P_N}({\varOmega _3})} \right\|_2})^2}\text{，}$

(15)

全息面测量声压总能量为：

$\begin{split}\\[-12pt]E = \sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {p{{({x_i},{y_j})}^2}} } = & \frac{1}{{MN}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {p{{({k_x}_i,{k_{yj}},{z_H})}^2}} }=\\& \frac{1}{{MN}}{({\left\| {p({k_x},{k_y},{z_H})} \right\|_2})^2}\text{，}\end{split}$

(16)

将式（16）代入式（10）可得：

$SNR \approx {\kern 1pt} 10\lg \frac{{b{{({{\left\| {p({k_x},{k_y},{z_H})} \right\|}_2})}^2} - MN{{({{\left\| {{P_N}({\Omega _3})} \right\|}_2})}^2}}}{{MN{{({{\left\| {{P_N}({\Omega _3})} \right\|}_2})}^2}}}\text{。}$

(17)

3 信噪比估值判别

由于噪声信号平稳随机分布，当全息面的位置和大小确定时，实际的全息面信噪比也随之确定。为便于仿真分析，会向全息面声压数据中添加一定信噪比下的噪声。以添加的信噪比值作为理论信噪比值，研究利用式（17）进行信噪比估计的估值误差。

假设某一全息面下理论信噪比值为 SNR，信噪比估值为SNR’，记估值误差为 $\varepsilon $ ，其表达式如下

$\varepsilon {\rm{ = }}\frac{{\left| {SNR' - SNR} \right|}}{{SNR}}\text{。}$

(18)

由式可知， $\varepsilon $ 出现的根本原因是将 ${\varOmega _3}$ 区域内的波数成分全部视为噪声信号的波数成分，而事实上该区域内的波数成分依然是声压信号和噪声信号波数的混合。因此， $\varepsilon $ 的大小与 ${\varOmega _3}$ 区域内的声压信号衰减程度密切相关。从图 1 可以看出，k_max 越大， ${\varOmega _3}$ 区域内的有用声压信号衰减程度就越高，ε 值就越小，估值也就越准确。由采样定理，波数域内不发生混迭的最高波数成分 ${k_{\max }} = \pi /\Delta $ ， $\Delta $ 越小，估值越准确。如果使采样间隔 $\Delta $ 不变，只在一定范围内改变全息面的大小，则信噪比估值应该近似。但是在实际测量中，为节约成本，一般只测量 1 次，所以，可以选取该全息面内不同区域的数据进行重复估计。

下面以 2 个点声源为例进行仿真：2 点源中心坐标分别取（0, 0.25, 0）和（0, –0.25, 0），点源强度为 0.001 m³/s；分析频率f = 1 000 Hz，声速取 340 m/s，分析波长 $\lambda = 0.34 {\rm{m}}$ ；取 $\Delta = 0.062 5 {\rm{m}}$ ， $L = 2 {\rm{m}}$ ，全息面Z_H = 0.07 m，以全息面坐标原点为中心，从全息面中选取 9 个正方形区域 ${L_i} \times {L_i}(i = 1,2 \cdots 9)$ ，其中L_i 由下式确定：

${L_i} = L - 2(i - 1)\Delta {\text{，}}i = 1,2 \cdots 9{\text{。}}$

(19)

由式（9）可得 ${L_9}{\rm{ = }}1 {\rm{m}}$ ，并得到 9 个信噪比估值 $SN{R'_i}{\kern 1pt} {\kern 1pt} (i = 1,2 \cdots 9)$ ，分别找到其最大估值 $SN{R_{\max }}$ 和最小估值 $SN{R_{\min }}$ ，仿真结果如图 2 所示。

由图 2 可发现，当理论信噪比小于 25 dB 时，理论值和估值极为接近，而且此时 $SN{R_{\max }}$ 和 $SN{R_{\min }}$ 也非常相近；当理论信噪比大于 25 dB 时，理论值与估值的差值越来越大，估值误差迅速增加。同时， $SN{R_{\max }}$ 和 $SN{R_{\min }}$ 的距离也逐渐增大。在理论信噪比为 25 dB 时， $SN{R_{\max }}$ 为 24.62 dB， $SN{R_{\min }}$ 为 24.07 dB，估值误差 $\varepsilon $ 仅为 1.52%。假定对估值误差的要求为 ${\varepsilon _r}$ ，令 ${\varepsilon _r} = 3\% $ ，则可认为，在 25 dB 以下的理论信噪比，其估值都精确。也就是说，在 ${\varepsilon _r} = 3\% $ 的条件下，采样间隔 $\Delta = 0.062 \ 5 {\rm{m}}$ 所对应的最大信噪比估值是 25 dB。

事实上，理论信噪比未知，只能得到估计值 $SN{R_{\max }}$ 和 $SN{R_{\min }}$ ，因此需要对估值误差 $\varepsilon $ 进行修正。记修正后的估值误差为 $\varepsilon '$ ，其表达式为：

$\varepsilon ' = \frac{{\left| {SN{R_{\max }} - SN{R_{\min }}} \right|}}{{SN{R_{\max }}}}{\text{。}}$

(20)

如果 $\varepsilon ' < {\varepsilon _r}$ ，就认为估值精确。理论信噪比为 25 dB 时，有 $\varepsilon ' = 2.35\% < 3\% $ ，满足精度要求。

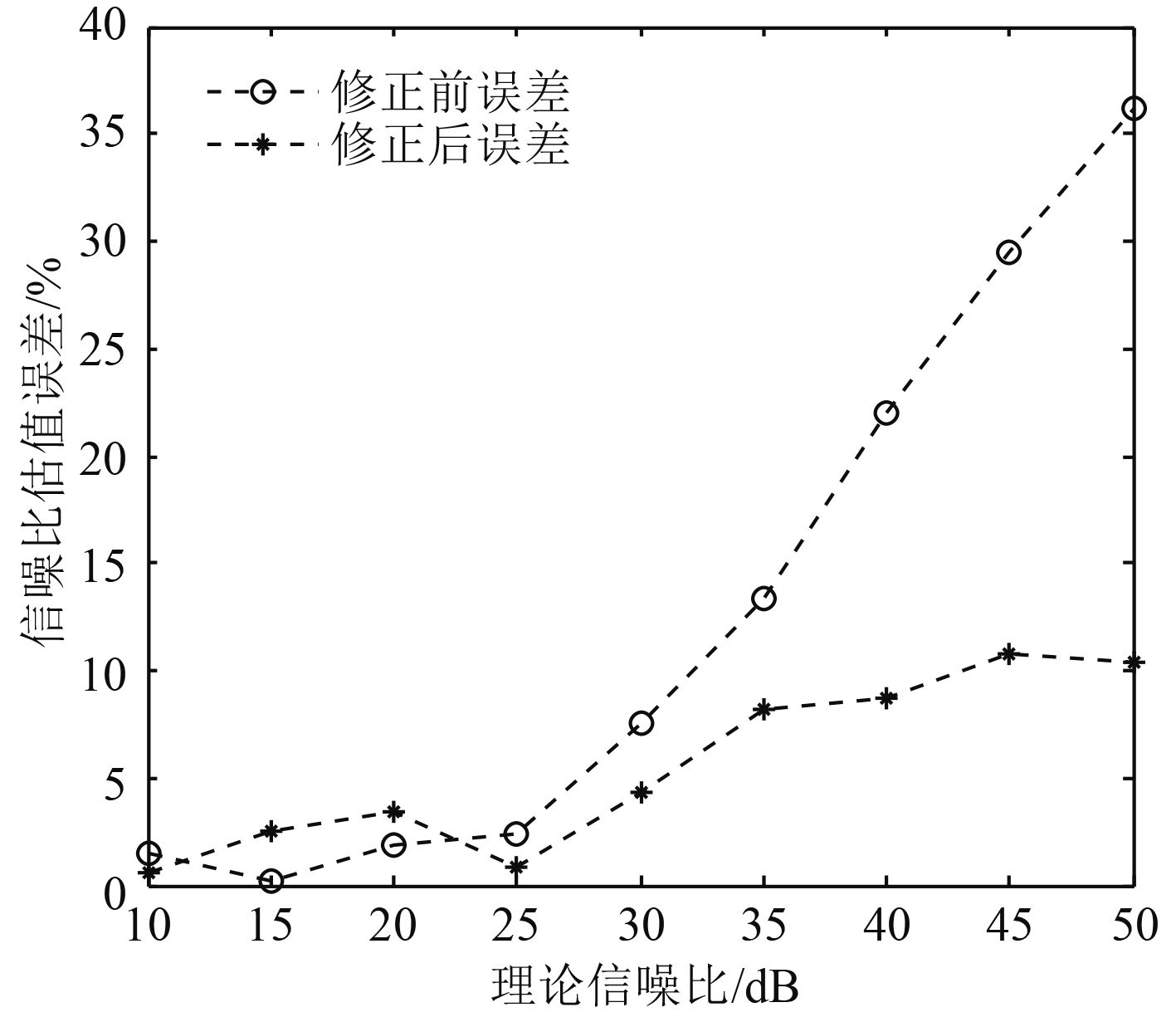
在同样仿真条件下，修正前后的误差对比如图 3 所示。

由图 3 可看出，修正后的估值误差 $\varepsilon '$ 不会随着信噪比的增加而一直增大，而是分为 3 个阶段，第 1 阶段信噪比区间为 10～25 dB， $\varepsilon '$ 在 3% 左右波动；第 2 阶段信噪比区间为 25～35 dB， $\varepsilon '$ 逐渐增大到 10% 左右；第 3 阶段信噪比区间为 30～50 dB， $\varepsilon '$ 基本稳定在 10%。

在对信噪比估值进行判别时，如果取 ${\varepsilon _r} = 15\% $ ，可以发现在理论信噪比为 50 dB 时，信噪比估值只有 32 dB，真实的估值误差 $\varepsilon $ 高达 36%，但修正后的估值误差 $\varepsilon '$ 只有 10%，这显然不合理。所以，在进行估值判别时要合理选择 ${\varepsilon _r}$ 。考虑到信噪比越高，噪声干扰越小，对全息重构的影响也就越小， ${\varepsilon _r}$ 可以随着信噪比的增加而适当增加。通常情况下，信噪比小于 25 dB 时，一般要求 ${\varepsilon _r}$ 在 3% 左右，最高不超过 10%。

综合以上分析，信噪比估值的判别方法如下：

1）保持采样间隔 $\Delta $ 不变，以全息面坐标原点为中心，选择合适的n 值（可以令 ${L_n} = L/2$ ），从全息面中选择n 个正方形区域 ${L_i} \times {L_i}(i = 1,2 \cdots n)$ ；

2）对所取区域的声压数据分别进行信噪比估计，得到一系列估值 $SN{R'_i}$ ，找到其最大估值 $SN{R_{\max }}$ 和最小估值 $SN{R_{\min }}$ ，并计算 $\varepsilon '$ ；

3）根据实际测量情况，选择合适的 ${\varepsilon _r}$ ，如果 $\varepsilon ' < {\varepsilon _r}$ ，认为估值精确，并将 $SN{R_{\max }}$ 作为理论信噪比值。

4 减小信噪比估值误差的方法

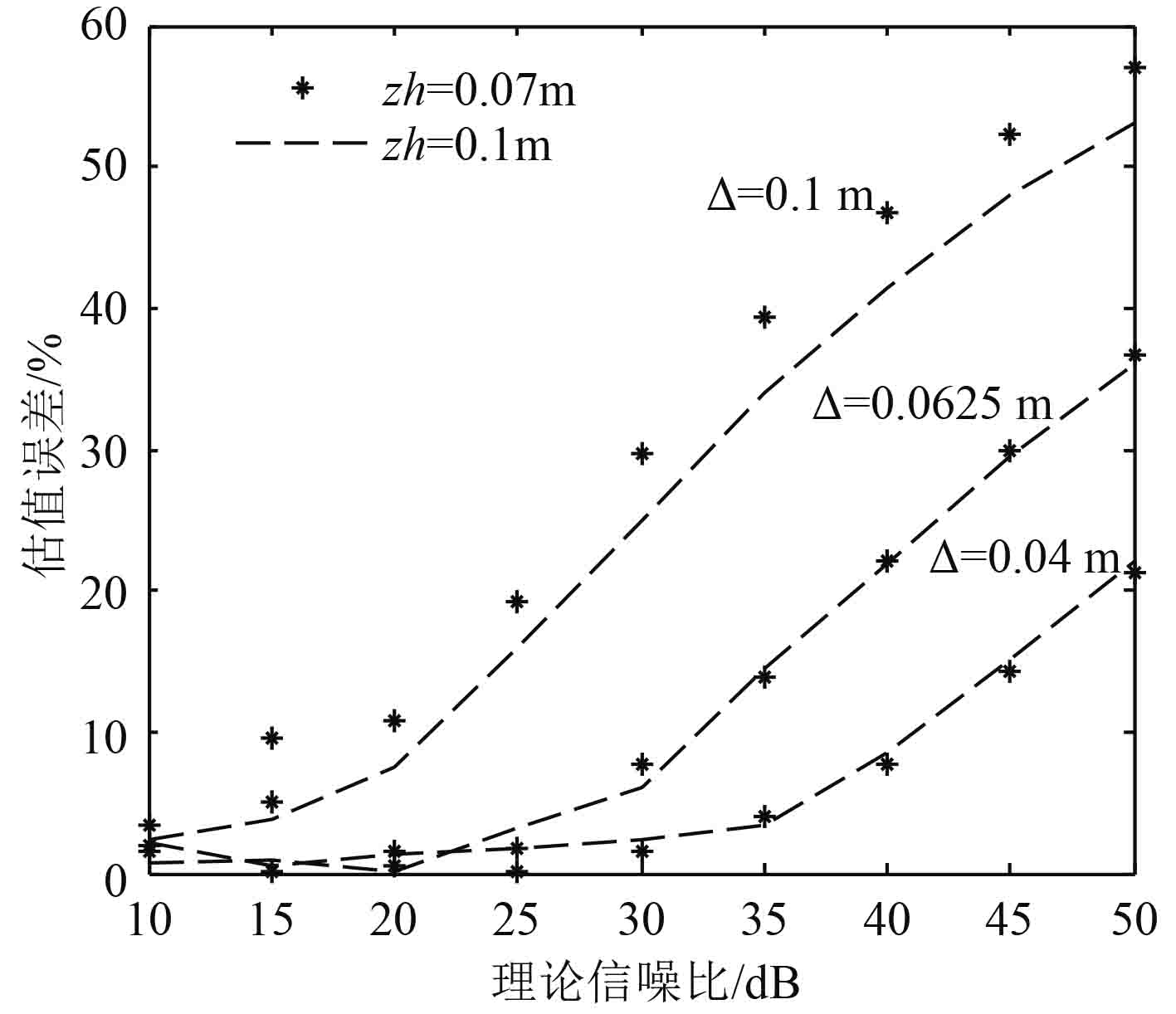
如果判别后发现信噪比估值不准确，可以通过减少全息面采样间隔 $\Delta $ 来提高估值的准确性以降低估值误差。但减小全息面采样间隔进行第 2 次测试时，全息面大小能够保持不变，但是其位置可能会发生细微变化。因此选择 2 个不同位置的全息面，在不同采样间隔下进行仿真，结果如图 4 所示。

从图 4 可看出，采样间隔一定时， $\varepsilon $ 值随着信噪比的增加急剧增加；而信噪比一定时，尤其是在高信噪比区域， $\varepsilon $ 值随着采样间隔的减小迅速降低。而且，在 $\Delta \leqslant 0.0625 {\rm{m}}$ 时，只要 $\Delta $ 不变，即使全息面的位置发生变化， $\varepsilon $ 值也几乎不变，这为测试工作提供了方便。

实际测试中，如果全息面大小不变，减小采样间隔就意味着测量点数会增加，相应的工作量以及测量成本也会随之增加。为方便测量工作，表 1 给出了 ${\varepsilon _r}$ 不同时，不同采样间隔所对应的最大信噪比估值。实际测量中，可以根据测试环境、声源可能的分布状况等综合考虑，参照表 1，选择合适的全息面采样间隔，在使信噪比估值误差满足要求时尽可能减少测量点数。

5 结　语

本文通过分析波数域内噪声信号的分布情况，提出波数域内的全息面信噪比估计公式，并根据该估值公式分析了信噪比估值误差的来源，指出全息面采样间隔对估值误差具有重要影响。提出了一种选择不同区域的全息数据进行重复估计的方法对信噪比估值进行判断，并指出可以通过减小采样间隔来减降低信噪比估值误差。以两点源为例进行仿真，给出了在不同采样间隔下满足不同精度条件的最大信噪比估值，为实际应用提供参考。