0 引 言

被动声呐探测通过接收水中目标辐射的噪声，来对目标进行定位。因其本身不发射信号，具有隐蔽性好，不易受攻击等优点，而备受海军关注。单个被动传感器只能观测到目标的方位，无法得到距离信息，属于不完全观测，要完成目标的跟踪任务需融合多个传感器的信息。因此，对被动多传感器跟踪系统的研究势在必行 ^{[ 1]} 。

对被跟踪的目标当前状态参数的估计维持，与此同时，将传感器所接收到的量测数据进行处理的整个过程被称为一个目标跟踪过程 ^{[ 2]} 。被动跟踪的量测方程为非线性，传统的线性卡尔曼滤波 ^{[ 1]} 无法得到解析解。对于非线性系统，需要用非线性滤波。非线性滤波典型的算法有扩展卡尔曼滤波 ^{[ 1]} 与无迹卡尔曼滤波等，这些算法只能处理弱非线性系统，且受高斯噪声的限制。近年来，粒子滤波在处理非线性非高斯问题中得到了广泛应用。它是一种基于贝叶斯滤波用“粒子”概率密度表示的序贯蒙特卡罗方法，所谓粒子就是一些具有相应权值的随机样本，理论上当粒子数无限时，这些随机样本就能准确地拟合后验概率分布，算法精度逼近最优。标准的粒子滤波为解决样本退化问题，在递推过程中引进重采样思想，但随之而来的问题是样本多样性的匮乏 ^{[ 3]} 。文献[ 4]提出了基于均匀重采样的粒子滤波器（AUPF），在重采样过程中，大部分权值大的粒子仍按照随机抽样得到，其余的粒子按均匀分布抽取，均匀分布的最小值和最大值应取上次迭代中粒子的最小值和最大值，目的是保留被抛弃粒子的分布范围。该方法在减小粒子退化程度的同时，增加了粒子多样性。

目标在运动过程中不断变化，从一种形式变换为另一种形式，这就是所谓的目标机动 ^{[ 5]} 。单一的运动模型不能准确的描述机动目标的运动方式，交互式多模型（IMM）算法通过马尔可夫转移概率对多模型进行切换，能跟踪目标的任意机动，因此在机动目标跟踪中交互式多模型算法是一种有效的方法。文献[ 6]将 IMM 与 PF 相结合得到了 IMM-PF 算法，但标准粒子滤波算法的粒子多样性匮乏，本文在文献[ 4]的基础上，结合 IMM，提出了 IMM-AUPF 算法，并通过仿真验证了该方法的有效性。

1 被动跟踪模型 1.1 离散状态方程

目标运动模型可以用离散状态方程表述为：

${ X}\left( {k + 1} \right) = { F}X(k) + { G}v(k)\text{，}$

(1)

式中： X 为系统状态向量； F 为状态转移矩阵； G 为状态噪声输入矩阵； v（ k）为零均值、协方差为 Q 的白高斯过程噪声。

常见的目标运动模型主要有匀速（ CV）模型、匀加速（ CA）模型和恒速率转弯（ CT）模型。在此仅对本文采用的以下 2 种模型进行叙述，均考虑二维情况。

1） CV 模型

该模型假设目标的加速度为 0，状态向量可以简化为 $X = [x,y,{v_x},{v_y}]$ ，4 个量分别表示目标各方向的位置、速度分量，矩阵 F 和 G 为：

$\begin{array}{l}{ F} = \left[ {\begin{array}{*{20}{l}}{1\quad 0\quad T\quad 0}\\{0\quad 1\quad 0\quad T}\\{0\quad 0\quad 1\quad 0}\\{0\quad 0\quad 0\quad 1}\end{array}} \right]\text{，}\\{ G} = \left[ {\begin{array}{*{20}{l}}{{T^2}/2\quad 0\quad T\quad 0}\\{0{T^2}/2\quad 0\quad T}\end{array}} \right]\text{。}\end{array}$

2） CT 模型

该模型为恒速率转弯模型，状态向量可以写为： ${ X} = [x,y,{v_x},{v_y}]$ ，4 个量分别表示目标各方向的位置、速度分量，矩阵 F 和 G 为：

$\begin{array}{l}{ F} = \left[ {\begin{array}{*{20}{c}}1 & 0 & {\displaystyle\frac{{\sin \omega T}}{\omega }} & {\displaystyle\frac{{\cos \omega T}}{\omega }}\\[8pt]0 & 1 & {\displaystyle\frac{{1 - \cos \omega T}}{\omega }} & {\displaystyle\frac{{\sin \omega T}}{\omega }}\\[8pt]0 & 0 & {\cos \omega T} & { - \sin \omega T}\\[8pt]0 & 0 & {\sin \omega T} & {\cos \omega T}\end{array}} \right]\text{，}\\[45pt]{ G} = \left[ \begin{array}{l}{T^2}/2\quad 0\quad \quad 0\\0\quad \quad {T^2}/2\quad 0\end{array} \right]\text{。}\end{array}$

式中 ω 为运动角速度，即代表模型机动情况的参数，rad/s。

1.2 离散观测方程

目标量测模型可以用离散状态方程表述为：

${ Y}\left( {k + 1} \right) = {h_k}\left( {{x_k}} \right) + {\omega _k}\text{，}$

(2)

式中： Y 为系统测量向量； h _k （ x _k ）为非线性函数； ω（ k）是零均值、协方差为 R 的白高斯过程噪声。

在被动纯方位目标跟踪中有：

${h_k}\left( {{x_k}} \right) = {\left[ {atg\frac{{x - {x_1}}}{{y - {y_1}}}, \cdots ,atg\frac{{x - {x_i}}}{{y - {y_i}}}, \cdots } \right]^{\rm T}}\text{。}$

(3)

式中 i = 1,2，…， N 为被动传感器的个数。

2 AUPF算法 2.1 标准的粒子滤波算法 ^{[ 7]}

粒子滤波是一种基于蒙特卡罗方法和递推贝叶斯估计的统计滤波方法，它依据大数定理采用蒙特卡洛罗方法来求解贝叶斯估计中的积分运算。其基本思想是：首先根据系统状态向量的初始均值和方差，产生一组随机样本的集合，称这些样本为粒子，然后根据系统的状态方程进行下一时刻粒子状态的预测，再根据量测不断调节粒子的权重和位置，通过调整后的信息去逼近状态的后验概率分布。

假设动态系统 k 时刻目标状态的后验概率分布 $p\left( {{x_k}/{z_k}} \right)$ 可由从转移先验密度函数 $p\left( {{x_k}/{x_{k - 1}}} \right)$ 中随机抽取的 N 个样本 $\left\{ {{x^i}_k,{\omega ^i}_k} \right\}$ 来描述。权值 ${\omega ^i}_k$ 被归一化为 $\sum {{\omega ^i}_k} = 1$ ，则 k 时刻目标状态的后验概率分布可离散地加权为：

$p\left( {{x_k}/{z_k}} \right) \approx \sum\limits_{i = 1}^N {{\omega ^i}_k \cdot \delta \left( {{x_k} - {x^i}_k} \right)} \text{，}$

(4)

权值通过重要采样法选择，粒子集可由重要性密度函数 $q\left( {{x_k}/{x_{k - 1}},{z_k}} \right)$ 得到，权值为：

${\omega ^i}_k \propto {\omega ^i}_{k - 1}\frac{{p\left( {{z_k}/{x^i}_k} \right) \cdot p\left( {{x^i}_k/{x^i}_{k - 1}} \right)}}{{q\left( {{x^i}_k/{x^i}_{k - 1},{z_k}} \right)}}\text{，}$

(5)

标准粒子滤波算法选择最易于实现的先验概率密度作为重要性函数，即

$q\left( {{x^i}_k/{x^i}_{k - 1},{z_k}} \right) = p\left( {{x^i}_k/{x^i}_{k - 1}} \right)\text{，}$

(6)

则重要性权值可简化为：

${\omega ^i}_k \propto {\omega ^i}_{k - 1} \cdot p\left( {{z_k}/{x^i}_k} \right)\text{。}$

(7)

标准粒子滤波的算法归纳如下：

1）初始化。由先验概率 $p\left( {{x_0}} \right)$ 产生粒子群 $\left\{ {{x^i}_0} \right\}_{i = 1}^N$ 。

2）所有粒子权值为 $\displaystyle\frac{1}{N}$ 。

3）预测。在 k 时刻，根据状态转移方程预测下一时刻粒子的值 ${x^i}_k$ 和观测值 ${h_k}\left( {{x^i}_k} \right)$ 。

4）更新。按式（7）更新粒子权值，并且归一化。

5）重采样。得到新的粒子集合 $\left\{ {{x^{{i^*}}}_{_k},i = 0,1,2, \cdots ,N} \right\}$ 。则可得 k 时刻状态的最小均方估计为： $\overline x \approx \sum\limits_{i = 1}^N {{\omega ^i}_k \cdot {x^i}_k} $ 。

6）时刻 k = k + 1，转到第 2 步。

标准粒子滤波引进随机重采样过程，虽然解决了粒子退化的问题却又引入了样本贫化现象。标准粒子滤波选用先验概率分布作为重要性密度函数，没有考虑新的观测信息，随着时间的增加，粒子的权重集中到少数粒子上，甚至在经过几步的递归之后，可能只有一个粒子有非零权值，其他粒子粒子权值很小，可以忽略不计，这将导致粒子贫化。

2.2 AUPF 粒子滤波算法 ^{[ 4, 8]}

为保证粒子的多样性，AUPF 在重采样中引入均匀分布的思想，在保证粒子对真实后验概率密度逼近能力的情况下，使粒子具有比较广的分布范围。

均匀重采样的具体步骤如下：

1）对所有的 N 个粒子按权值进行排序，选出权值最大的 N _s 个粒子，其中 ${N_s} = nN\left( {0.8 < n < 1} \right)$ ；

2）计算粒子的概率累积和 $\left( {{a_j}} \right)_{i = 1}^{{N_s}}$ ，并假设 a ₀ = 0；

3）随机采样第 $i\left( {i = 1,2, \cdots ,{N_s}} \right)$ 个服从 [0 1] 均匀分布的数 η _i ，若 ${a_{j - 1}} < {\eta _i} < {a_j}$ ，则可以取得第 i 次随机采样的结果为 x _j ；

5）将 2 次得到的粒子合并，得到将要进入下一次迭代的全部粒子 $\left\{ {{x^i}_k} \right\}_{i = 1}^N$ ，并重新分配权值。

3 IMM 均匀重采样粒子滤波 3.1 IMM 算法介绍

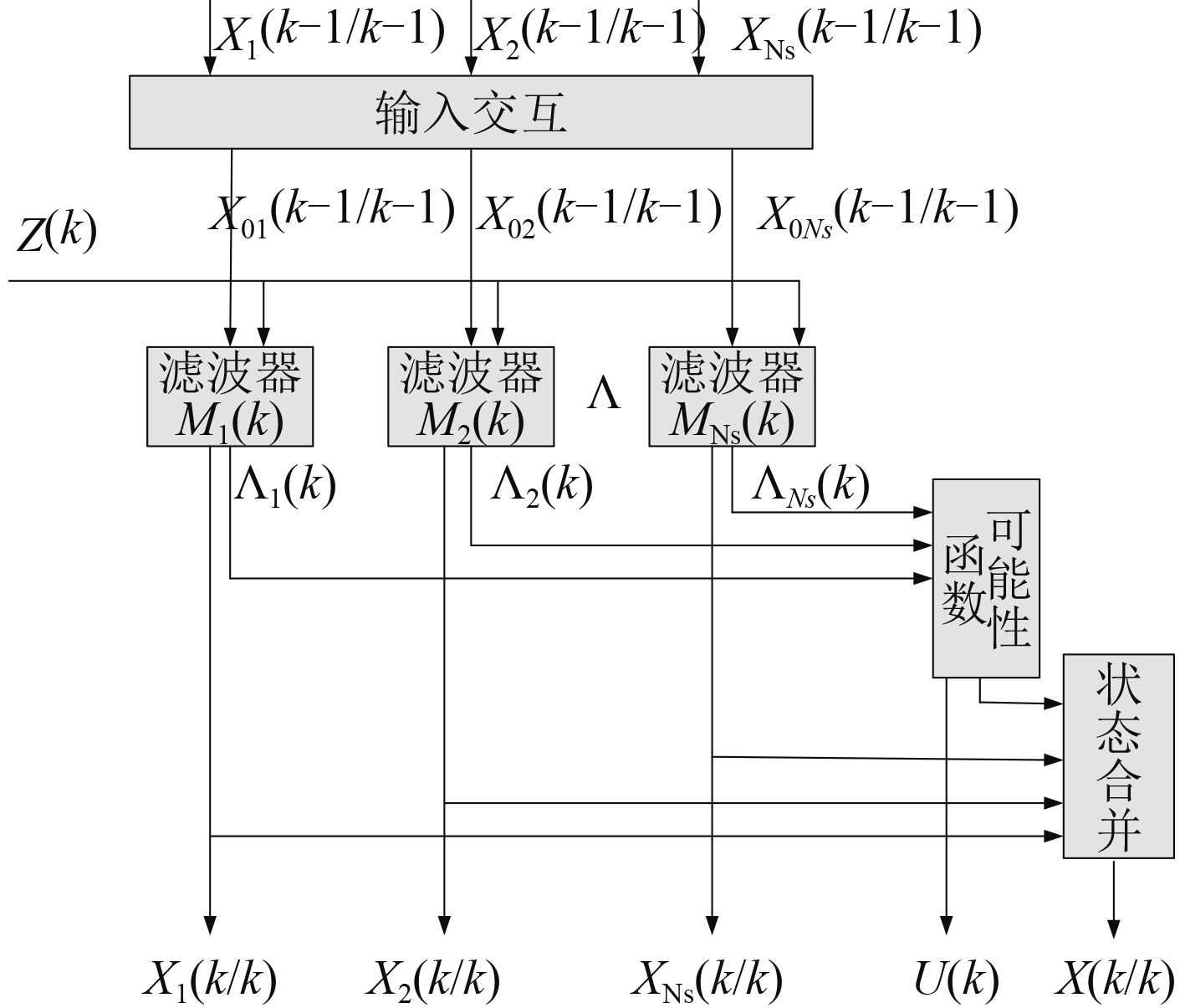
IMM 算法原理如 图 1 所示。IMM ^{[ 9]} 算法：混合概率计算、输入交互、模型滤波、模型概率更新及状态和协方差计算等步骤。

详细步骤的描述见 IMM-AUPF 算法。

3.2 IMM-AUPF 算法介绍

在 IMM 算法的模型滤波中应用 AUPF，即可得到本文的 IMM-AUPF 等。

IMM-AUPF 算法具体实现步骤如下：

1）输入交互 ^{[ 9]}

假设有 N _s 个模型，计算

$\overline {{c_{{l_1}}}} = \sum\limits_{i = 1}^{{N_s}} {{p_{{l_2}{l_1}}} \cdot {u_{k - 1,{l_2}}}} \text{，}$

(8)

$\overline {{c_{{l_1}}}} = \sum\limits_{i = 1}^{{N_s}} {{p_{{l_2}{l_1}}} \cdot {u_{k - 1,{l_2}}}} \text{，}$

(9)

${x^0}_{k - 1/k - 1,{l_1}} = \sum\limits_{{l_2} = 1}^{{N_s}} {{x_{k - 1/k - 1,{l_2}}} \cdot {u_{k - 1/k - 1,{l_2}/{l_1}}}} \text{，}$

(10)

$\begin{array}{l}{P^0}_{k - 1/k - 1,{l_2}} = \sum\limits_{{l_2} = 1}^{{N_s}} {{u_{k - 1/k - 1,{l_2}/{l_1}}}}\times \\\quad \left\{ \begin{array}{l}{P_{k - 1/k - 1,{l_2}}} + \left[ {{x_{k - 1/k - 1,{l_2}}} - {x^0}_{k - 1/k - 1,{l_1}}} \right]\\{\left[ {{x_{k - 1/k - 1,{l_2}}} - {x^0}_{k - 1/k - 1,{l_1}}} \right]^T}\end{array} \right\}\text{。}\end{array}$

(11)

2）并行滤波

从 $N\left( {{x^0}_{k - 1/k - 1,{l_1}},{P^0}_{k - 1/k - 1,{l_1}}} \right)$ 中随机抽取样本点： ${x^{\left( i \right)}}_{k - 1/k - 1,{l_1}}\sim N\left( {{x^0}_{k - 1/k - 1,{l_1}},{P^0}_{k - 1/k - 1,{l_1}}} \right),i = 1, \cdots N;$ 根据状态转移方程进行粒子预测，得到新的粒子集 ${x^{\left( i \right)}}_{k - 1/k - 1,{l_1}}$ ，将其代入观测方程得到 ${z^{\left( i \right)}}_{k - 1/k - 1,{l_1}}$ ，计算残差：

${\delta ^{\left( i \right)}}_{k,{l_1}} = {z_k} - {z^{\left( i \right)}}_{k/k - 1,{l_1}}\text{。}$

(12)

更新权值，并归一化。

3）模型概率更新

预测观测的均值：

$\begin{array}{l}{S_{k,{l_1}}} = R + \sum\limits_{i = 1}^N {{\omega ^{\left( i \right)}}_{k,{l_1}} \cdot } \times\\\quad \quad \quad \left( {{z^{\left( i \right)}}_{k/k - 1,{l_1}} - \overline {{z_{k,{l_1}}}} } \right){\left( {{z^{\left( i \right)}}_{k/k - 1,{l_1}} - \overline {{z_{k,{l_1}}}} } \right)^{\rm T}}\text{，}\end{array}$

(13)

新息：

${v^{{l_1}}} = {z_k} - \overline {{z_{k,{l_1}}}}\text{，}$

(14)

似然函数：

${\Lambda _{k,{l_1}}}\sim N\left( {{v_{k,{l_1}}};0,{S_{k,{l_1}}}} \right)\text{，}$

模型概率：

${u_{k,{l_1}}} = \frac{1}{c}{\Lambda _{k,{l_1}}} \cdot \overline {{c_{{l_1}}}} \text{。}$

(15)

式中：

$c = \sum\limits_{i = 1}^N {{\Lambda _{k,{l_1}}} \cdot \overline {{c_{{l_1}}}} } \text{。}$

(16)

4）重采样

从 $\left\{ {{x^i}_{k/k - 1,{l_1}},i = 1, \cdots ,{N_s}} \right\}$ 中根据重要性权值利用均匀重采样方法，重新采样得到 1 组新的粒子 $\left\{ {{x^j}_{k/k - 1,{l_1}},j = 1, \cdots ,{N_s}} \right\}$ ，并重新分配权值 ${\omega ^{\left( i \right)}}_{k,{l_1}} = \frac{1}{N}$ 。

5）状态估计及协方差

${x_{k/k,{l_1}}} = \sum\limits_{j = 1}^N {{\omega ^{\left( j \right)}}_{k,{l_1}}{x^{\left( j \right)}}_{k/k,{l_1}}}\text{，} $

(17)

$\begin{array}{l}{P_{k/k,{l_1}}} = \displaystyle\sum\limits_{j = 1}^N {{\omega ^{\left( j \right)}}_{k,{l_1}} \cdot } \times\\\quad \quad \quad \left[ {{x_{k/k,{l_1}}} -\displaystyle {x^{\left( j \right)}}_{k/k,{l_1}}} \right]{\left[ {{x_{k/k,{l_1}}} - {x^{\left( j \right)}}_{k/k,{l_1}}} \right]^{\rm T}}\text{。} \end{array}$

(18)

6）输出交互

根据各自滤波器的估计结果及其模型后验概率，计算最终状态估计：

${x_{k/k}} = \sum\limits_{{l_1} = 1}^{{N_s}} {{x_{k/k,{l_1}}}{u_{k,{l_1}}}}\text{。} $

(19)

4 仿真验证与比较 4.1 精度评价指标 ^{[ 8]}

采用的评价指标如下：单次运行的均方根误差曲线图用以定性比较；多次运行的均方根误差（Root-Mean-square-Error，简称 RMSE）以定量比较。单次运行的均方根误差通过下式计算:

$RMSE = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{x_k} - \overline {{x_k}} } \right)}^2}} } \text{。}$

(20)

式中： x _k 为目标状态真实值； $\overline {{x_k}} $ 为估计值； N 为时间步长数。

J 次蒙特卡洛试验的 RMSE 均值:

$\mu = \frac{1}{J}\sum\limits_{i = 1}^J {RMS{E_i}} \text{，}$

(21)

J 次蒙特卡洛试验的 RMSE 均方差:

$\sigma = \sqrt {\frac{1}{J}\sum\limits_{i = 1}^J {{{\left( {RMS{E_i} - \mu } \right)}^2}} } \text{。}$

(22)

4.2 仿真分析

设目标的状态矢量为 ${X_k}\mathop \Delta \limits_ = \left[ {{x_k},{y_k},{v_{k,x}},{v_{k,y}}} \right]$ ，其中，4 个量分别为目标的位置和速度。假定 3 个传感器成正三角形，若前 2 个传感器的位置为（–8 000，–3 500），（–2 000，–3 500），第 3 个传感器的横坐标 x ₃ 为 –5 000，则 ${y_3} = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} - {{\left( {{x_3} - {x_1}} \right)}^2}} - \left| {{y_1}} \right|$ ，粒子数为 300，方位测量误差为 0.1°。

目标轨迹设置如下：目标起始位置为（0，0），采样间隔为 T = 1 s，目标初始速度为 v = 340 m/s，前 20 个采样间隔沿与水平方向成 10° 的方向做匀速直线运动，之后左转弯，转弯速率为 7.84°/s，持续时间为 25 个采样间隔，在第 46 ~ 60 个采样间隔内匀速运动，之后再以转弯速率为 7.84°/s 进行右转弯，持续到 80 个采样间隔，然后以 7.84°/s 继续右转弯，持续时间为 10 个采样间隔，最后在第 91 ~ 100 个采样间隔内匀速运动。

这里采用的模型集为匀速直线运动模型和 2 个恒速率转弯模型，其中 1 个描述目标逆时针转弯，另 1 个对应目标顺时针转弯。各模型之间的马尔可夫概率转移矩阵设定为：

${ p} = \left[ \begin{array}{l}0.9\quad 0.05\quad 0.05\\0.2\quad 0.795 0.005\\0.2\quad 0.005 0.795\end{array} \right]\text{。}$

3 个模型的初始概率为 u ₁（0）= 0.9， u ₂（0）= 0.05 和 u ₃（0）= 0.05。初始协方差矩阵设定为 ${ P}\left( 0 \right) = diag\left( {{{10}^{ - 6}} \times \left[ {400,400,100,100} \right]} \right)$ ，3 个模型的状态噪声方差为 100 m/s ²。

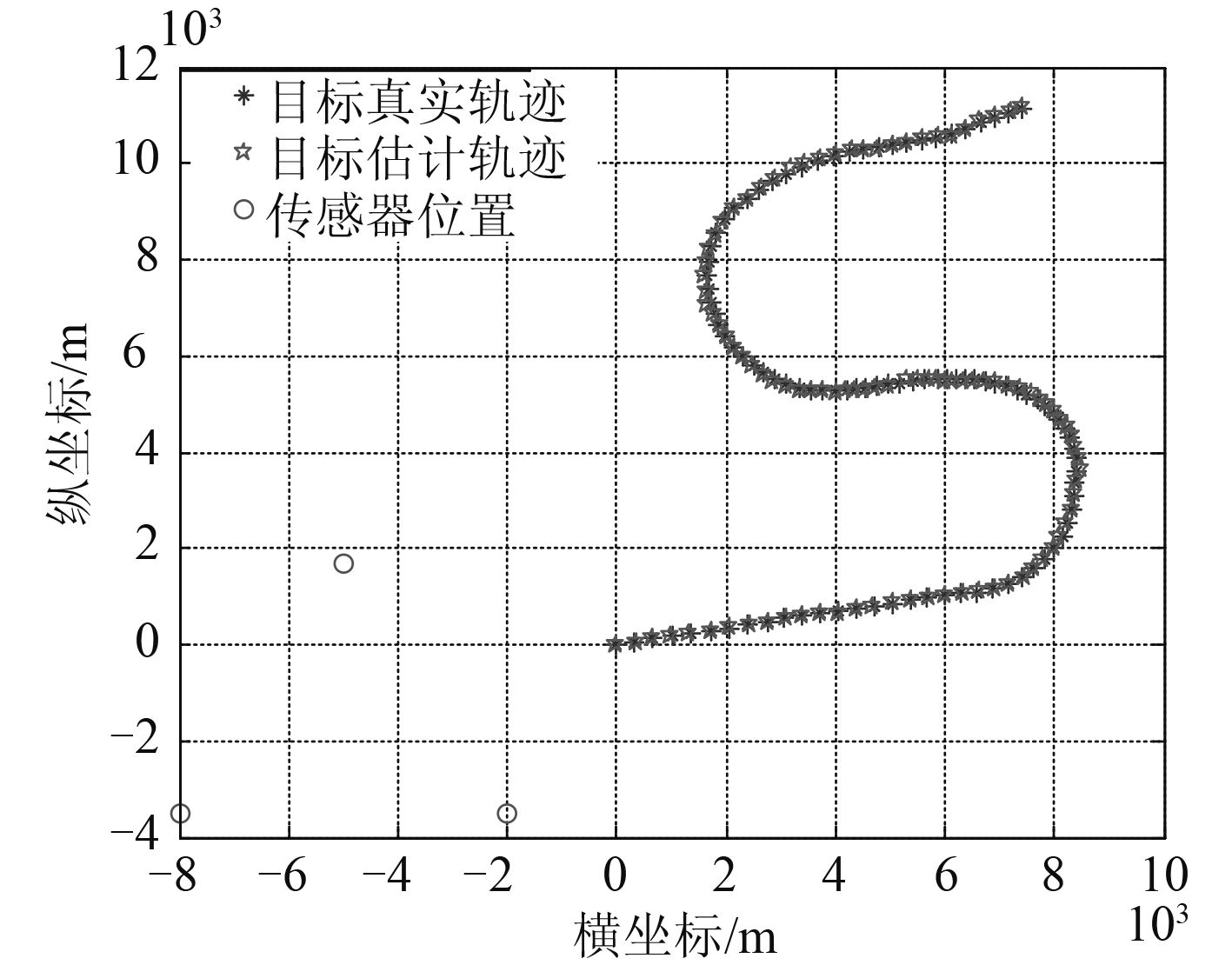
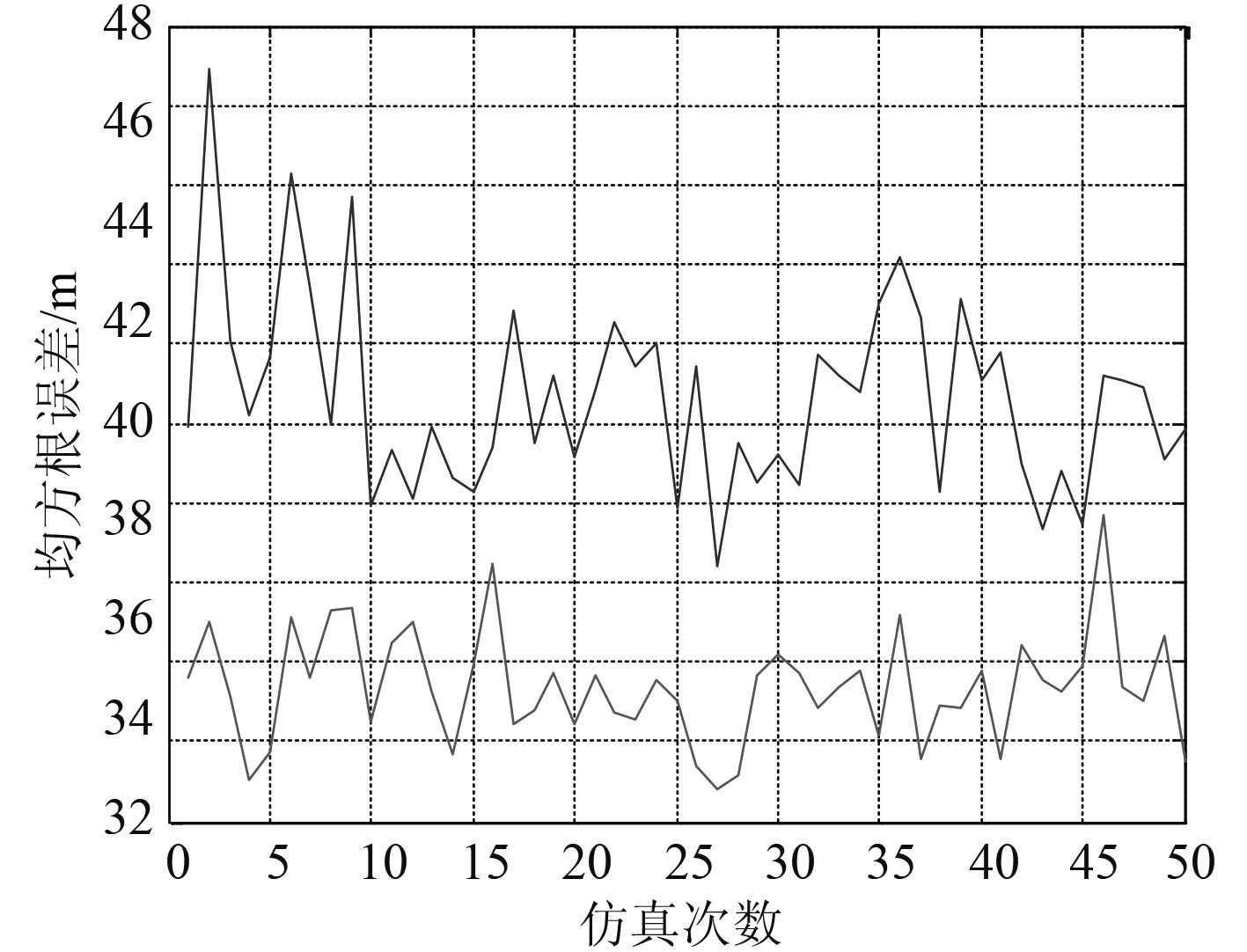
图 2 和 图 3 分别显示了 IMM-PF，IMM-AUPF 两种算法的航迹跟踪结果。 图 4 和 图 5 给出了 2 种方法所采用的 3 个模型在不同时刻的概率。 图 6 和 图 7 分别显示了 2 种方法每次蒙特卡罗仿真实验的 x， y 方向的位置估计的均方根误差。 表 1 和 表 2 分别显示了 2 种方法 50 次蒙特卡罗仿真后均方根误差的均值和方差对比结果。

从以上对比结果可看出，IMM-AUPF 算法的估计精度要优于 IMM-PF，这是因为前者在重采样过程中引进了均匀采样的思想，增加了粒子多样性，改善了样本贫化问题。

5 结 语

AUPF 算法在重采样中引入均匀分布的思想，在保证粒子对真实后验概率密度逼近能力的情况下，使粒子具有比较广的分布范围，增加了粒子的多样性，改善了粒子的贫化问题，使其对状态的估计精度有了进一步的提升。机动目标的跟踪最有效的方法是交互式多模型算法，在 IMM 算法的滤波阶段采用 AUPF，即为本文算法 IMM-AUPF，将其应用于被动多传感器系统中，在不完全观测的情况下，实现对机动目标的有效跟踪。将本文方法与 IMM-PF 算法进行对比，仿真结果表明本文方法的状态估计精度优于 IMM-PF。