为确保航母起降引导系统能精准地引导舰载机进行着舰,需定期对其进行标校。美国航母在码头驻泊时会安排对起降引导系统内各设备进行精度校准和系统下滑道一致性标校,一般采用先对跟踪雷达进行标校,然后将雷达的测量值作为真值,检查其他设备的性能和数据的一致性[1],此方法对国内航母起降引导系统岸基标校具有一定的参考意义。
由于着舰引导雷达具有较高的测距精度,中线电视具有较高的测角精度,文献[2]将着舰引导雷达的测距信息和中线电视的测角信息进行处理,实现两站联合定位,但在空间匹配上未考虑船体变形,具有一定的局限性;文献[3]提出在靶场试验中,用光电经纬仪和雷达联合定位,用几何法给出了解析解并分析了误差模型,但只是简单的融合;也有一些文献[4-5]提出了基于红外的测角信息和雷达的测角/测距信息双模制导系统,可以有效极高目标跟踪定位性能,但是该系统默认雷达和红外在同一位置处,未考虑设备在不同位置时的测量误差传递信息。基于以上分析,本文将着舰引导雷达的测角/测距信息与中线电视的测角信息进行了有效的融合和目标定位,并进行仿真验证,结论表明该方法计算简单且具备较高的定位精度,相应的标校方案具有一定的有效性和优越性。
1 雷达/电视测量模型 1.1 建立坐标系 1.1.1 甲板固连坐标系甲板固连坐标系相对于航母甲板固定不变,着舰引导雷达测量坐标系、中线电视测量坐标系和理想着舰点测量坐标系均属于甲板固连坐标系。3 个坐标系的坐标原点分别为着舰引导雷达天线安装标定点、电视镜头安装标定点和理想着舰点,其中中线电视测量坐标系与理想着舰点测量坐标系X 轴平行于斜角甲板降落跑道中线指向舰尾方向,Y 轴平行于甲板面且垂直于X 轴指向舰右舷,Z 轴平行于甲板面指向上,着舰引导雷达坐标系X 轴平行于舰首尾线指向舰尾方向,Y 轴平行于甲板面且垂直于X 轴指向舰右舷,Z 轴平行于甲板面指向上,X 轴方向为方位 0°,左侧为负,右侧为正,俯仰以XOY 平面为 0°,上为正,下为负。
1.1.2 水平坐标系水平坐标系坐标XOY 平面平行于水平面,X 轴指向正东,Y 轴指向正北,Z 轴垂直于水平面指向上,着舰引导雷达、中线电视、理想着舰点水平坐标系原点分别与对应的甲板固连系原点重合。
1.2 着舰引导雷达测量模型当着舰引导雷达跟踪上目标后,开始对目标的距离、方位、俯仰、多普勒径向速度及加速度进行测量,在某一时刻测量信息为:
| $\left\{ \begin{array}{l}{r_R} = {r_R}^\prime + {n_{rR}}\text{,}\\{\alpha _R} = {\alpha _R}^\prime + {n_{\alpha R}}\text{,}\\{\beta _R} = {\beta _R}^\prime + {n_{\beta R}}\text{。} \end{array}\right.$ | (1) |
式中:rR
,
目标在雷达测量坐标系下极坐标与直角坐标关系为:
| $\left[ \begin{array}{l}{x_R}\\{y_R}\\{z_R}\end{array} \right] = \left[ \begin{array}{c}{r_R}\cos {\beta _R}\cos {\alpha _R}\\{r_R}\cos {\beta _R}\sin {\alpha _R}\\{r_R}\sin {\beta _R}\end{array} \right]\text{。}$ | (2) |
式中:
当中线电视成功捕捉到目标后,数据处理后得到目标与十字丝的角度偏差,也能算得目标在中线电视坐标系下的方位角和俯仰角,在某一时刻中线电视测角模型为:
| $\left\{ \begin{array}{l}{\alpha _T} = {\alpha _T}^\prime + {n_{\alpha T}}\text{,}\\{\beta _T} = {\beta _T}^\prime + {n_{\beta T}}\text{。}\end{array} \right.$ | (3) |
式中:
目标在中线电视坐标系下极坐标与直角坐标关系为:
| $\left[ \begin{array}{l}{\alpha _T}^\prime \\\cos {\beta _T}^\prime \end{array} \right] = \left[ \begin{array}{l}\arctan \left( {\frac{{{y_T}}}{{{x_T}}}} \right)\\\arctan \left( {\frac{{{z_T}}}{{\sqrt {x_T^2 + y_T^2} }}} \right)\end{array} \right]\text{。}$ | (4) |
式中:xT ,yT ,zT 为相应时刻目标在中线电视坐标下的三维坐标值。
2 雷达/电视数据融合算法雷达/电视数据融合过程主要包括着舰引导雷达与中线电视数据的时空匹配和测量数据的融合。
2.1 雷达/电视数据的时空匹配 2.1.1 测量数据拟合算法研究表明,如果使用时间不匹配的多传感器数据进行融合,其融合后的性能有可能比单一传感器提供的更差[6-7],将各设备的测量数据进行时间上的关联,是数据融合的重要部分。
着舰引导雷达与中线电视测量初始时刻不一致,采样周期不同,故采用最小二乘拟合算法进行数据拟合[8],对于某组数据
| $S\left( x \right) = {a_1}{\varphi _1}\left( x \right) + {a_2}{\varphi _2}\left( x \right) + \cdots {a_n}{\varphi _n}\left( x \right)\text{,}$ | (5) |
求取基函数系数的法方程为:
| $\begin{split}\left[ {\begin{array}{*{20}{c}} {\left( {{\varphi _1},{\varphi _1}} \right)}&{\left( {{\varphi _1},{\varphi _2}} \right)}& \cdots &{\left( {{\varphi _1},{\varphi _n}} \right)}\\{\left( {{\varphi _2},{\varphi _1}} \right)}&{\left( {{\varphi _2},{\varphi _2}} \right)}& \cdots &{\left( {{\varphi _2},{\varphi _n}} \right)}\\ \vdots & \vdots & \ddots & \vdots \\{\left( {{\varphi _n},{\varphi _1}} \right)}&{\left( {{\varphi _n},{\varphi _2}} \right)}& \cdots &{\left( {{\varphi _n},{\varphi _n}} \right)}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{a_1}}\\{{a_2}}\\ \vdots \\{{a_n}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{{d_1}}\\{{d_2}}\\ \vdots \\{{d_n}}\end{array}} \right]\text{。}\end{split}$ | (6) |
式中:
着舰引导雷达与中线电视的测量数据均是在各自坐标系下完成测量的,在进行下滑道一致性标校时须将所有数据转换至理想着舰点坐标系下进行比较,此外,由于航母船体较大,在不同位置的船体姿态会存在差别,如果不进行修正会严重影响标校效果,应使用各设备附近的局部基准数据进行船体姿态修正。
雷达测量坐标系转换至理想着舰点地理坐标系,模型可表示为:
| $\left[ \begin{array}{l}{x_{RL}}\\{y_{RL}}\\{z_{RL}}\end{array} \right] = {{ T}_A}{{ T}_L}{ T}_R^{ - 1}\left[ \begin{array}{l}{x_R}\\{y_R}\\{z_R}\end{array} \right] + \left[ \begin{array}{l}{x_r}\\{y_r}\\{z_r}\end{array} \right]{\text{。}}$ | (7) |
式中:xr ,yr ,zr 为着舰引导雷达安装标定点在理想着舰点坐标系下的三维坐标。
| ${{T}_A} = \left[ {\begin{array}{*{20}{c}}{\cos {\varphi _c}}&{\sin {\varphi _c}}&0\\{ - \sin {\varphi _c}}&{\cos {\varphi _c}}&0\\0&0&1\end{array}} \right]\text{,}$ |
| $\begin{array}{l}{{T}_R} = \left[ {\begin{array}{*{20}{c}}{\cos {\gamma _R}}&{ - \sin {\gamma _R}}&0\\{\sin {\gamma _R}}&{\cos {\gamma _R}}&0\\0&0&1\end{array}} \right] \times\\ \left[ {\begin{array}{*{20}{c}}{\cos {\psi _R}}&0&{ - \sin {\psi _R}}\\0&1&0\\{\sin {\psi _R}}&0&{\cos {\psi _R}}\end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}}1&0&0\\0&{\cos {\theta _R}}&{ - \sin {\theta _R}}\\0&{\sin {\theta _R}}&{\cos {\theta _R}}\end{array}} \right]\text{。}\end{array}$ |
式中:
根据式(7)转换求得的目标相对理想着舰点坐标系下的三维坐标,可求得在此坐标系下的距离
由于中线电视只能测得角度信息,故在坐标系转换时可先假定距离为单位 1,进而可求得目标在中线电视坐标系下的三维坐标,后续坐标转换与雷达测量坐标系原理相同,只是将数据换成中线电视相应数据,不再赘述,可同样求得目标在理想着舰点坐标系下的方位角
着舰引导雷达在测距和测角上存在误差,中线电视也存在测角误差,将数据转换至理想着舰点坐标系的过程中存在有误差的传递,在分析误差传递过程中可做以下合理假设:
1)着舰引导雷达、中线电视及理想着舰点处的局部基准给出的船体姿态信息无误差;
2)着舰引导雷达、中线电视及理想着舰点在理想着舰点坐标系下的相互位置已知;
3)斜角甲板中线与首尾线的在甲板面上的夹角不变。
联合式(2)和式(7)对
| $\left[ \begin{array}{l}\Delta {x_{RL}}\\\Delta {y_{RL}}\\\Delta {z_{RL}}\end{array} \right] = M \cdot A \cdot \left[ {\begin{array}{*{20}{c}}{\Delta {r_R}}\\{\Delta {\alpha _R}}\\{\Delta {\beta _R}}\end{array}} \right]\text{。}$ | (8) |
式中:
| $\begin{array}{l}A\! = \!\left[ {\begin{array}{*{20}{c}}\!\!\!{\cos {\beta _R}\cos {\alpha _R}}\!\!\!&\!\!\!{ - {r_R}\cos {\beta _R}\sin {\alpha _R}}\\\!\!\!{\cos {\beta _R}\sin {\alpha _R}}\!\!\!&\!\!\!{{r_R}\cos {\beta _R}\cos {\alpha _R}}\\\!\!\!{\sin {\beta _R}}\!\!\!&\!\!\!0\end{array}} \right.\left. \begin{array}{l} \!\!\!- {r_R}\sin {\beta _R}\cos {\alpha _R}\\ \!\!\!- {r_R}\sin {\beta _R}\sin {\alpha _R}\\\!\!\!{r_R}\cos {\beta _R}\end{array}\right]\end{array}\!\!\!\!\text{,} $ |
| ${M} = {{T}_A} \cdot {{T}_L} \cdot {T}_R^{ - 1}\text{。}$ |
对坐标系转换后得到的
| $\left[ {\begin{array}{*{20}{c}}{\Delta {r_{RL}}}\\{\Delta {\alpha _{RL}}}\\{\Delta {\beta _{RL}}}\end{array}} \right] = B \cdot \left[ \begin{array}{l}\Delta {x_{RL}}\\\Delta {y_{RL}}\\\Delta {z_{RL}}\end{array} \right]\text{。}$ | (9) |
式中:
| $\begin{array}{l}B \!= \!\left[ \!\!\!\begin{array}{l}\frac{{{x_{RL}}}}{{\sqrt {x_{RL}^2 + y_{RL}^2 + z_{RL}^2} }}\\\frac{{ - {y_{RL}}}}{{x_{RL}^2 + y_{RL}^2}}\!\!\!\\\frac{{ - {x_{RL}}{z_{RL}}/\sqrt {x_{RL}^2 + y_{RL}^2} }}{{\left( {x_{RL}^2 + y_{RL}^2 + z_{RL}^2} \right)}}\end{array} \right.\left. {\begin{array}{*{20}{c}}{\frac{{{y_{RL}}}}{{\sqrt {x_{RL}^2 + y_{RL}^2 + z_{RL}^2} }}}\!\!\!\!&\!\!\!\!{\frac{{{z_{RL}}}}{{\sqrt {x_{RL}^2 + y_{RL}^2 + z_{RL}^2} }}}\!\!\!\!\\{\frac{{{x_{RL}}}}{{x_{RL}^2 + y_{RL}^2}}}\!\!\!\!&\!\!\!\!0\!\!\!\!\\{\frac{{ - {y_{RL}}{z_{RL}}/\sqrt {x_{RL}^2 + y_{RL}^2} }}{{\left( {x_{RL}^2 + y_{RL}^2 + z_{RL}^2} \right)}}}\!\!\!&\!\!\!{\frac{{\sqrt {x_{RL}^2 + y_{RL}^2} }}{{x_{RL}^2 + y_{RL}^2 + z_{RL}^2}}}\end{array}}\!\!\! \right]\end{array}\text{,}$ |
结合式(8)和式(9)可得:
| $\left[ {\begin{array}{*{20}{c}}{\Delta {r_{RL}}}\\{\Delta {\alpha _{RL}}}\\{\Delta {\beta _{RL}}}\end{array}} \right] = {BMA}\left[ {\begin{array}{*{20}{c}}{\Delta {r_R}^\prime }\\{\Delta {\alpha _R}^\prime }\\{\Delta {\beta _R}^\prime }\end{array}} \right]\text{。}$ | (10) |
误差协方差矩阵为:
| ${{P}_{RL}} = {BMA}{{P}_R}{\left( {{BMA}} \right)^{\rm{T}}}\text{。}$ | (11) |
可以看出,
根据以上分析可同样求得
将着舰引导雷达与中线电视测得的数据进行时空匹配后,可以进一步将测量的数据进行融合。
本文根据测量信息均方根误差最小的原则,采用加权平均法[9]进行数据融合,可以得到最后的目标位置:
| $\left\{ \begin{array}{l}{r_{RT}} = {r_{RL}}\text{,}\\[9pt]{\alpha _{TR}} = \sigma _{\alpha TR}^2\left( {\frac{{{\alpha _{TL}}}}{{\sigma _{\alpha TL}^2}} + \frac{{{\alpha _{RL}}}}{{\sigma _{\alpha RL}^2}}} \right)\text{,}\\[9pt]{\beta _{TR}} = \sigma _{\beta TR}^2\left( {\frac{{{\beta _{TL}}}}{{\sigma _{\beta TL}^2}} + \frac{{{\beta _{RL}}}}{{\sigma _{\beta RL}^2}}} \right)\text{,}\\[9pt]\sigma _{\alpha TR}^2 = \frac{{\sigma _{\alpha TL}^2\sigma _{\alpha RL}^2}}{{\sigma _{\alpha TL}^2 + \sigma _{\alpha RL}^2}}\text{,}\\[9pt]\sigma _{\beta TR}^2 = \frac{{\sigma _{\beta T}^2\sigma _{\beta R}^2}}{{\sigma _{\beta T}^2 + \sigma _{\beta R}^2}} \text{。}\end{array}\right.$ | (12) |
为验证文中提出的数据融合目标定位方法性能,假设目标距理想着舰点 6 km 处以 240 km/h 的速度沿 4°理想下滑道下滑着舰。着舰引导雷达以 30 Hz 频率进行目标跟踪测量,距离、方位角和俯仰角测量误差方差分别为
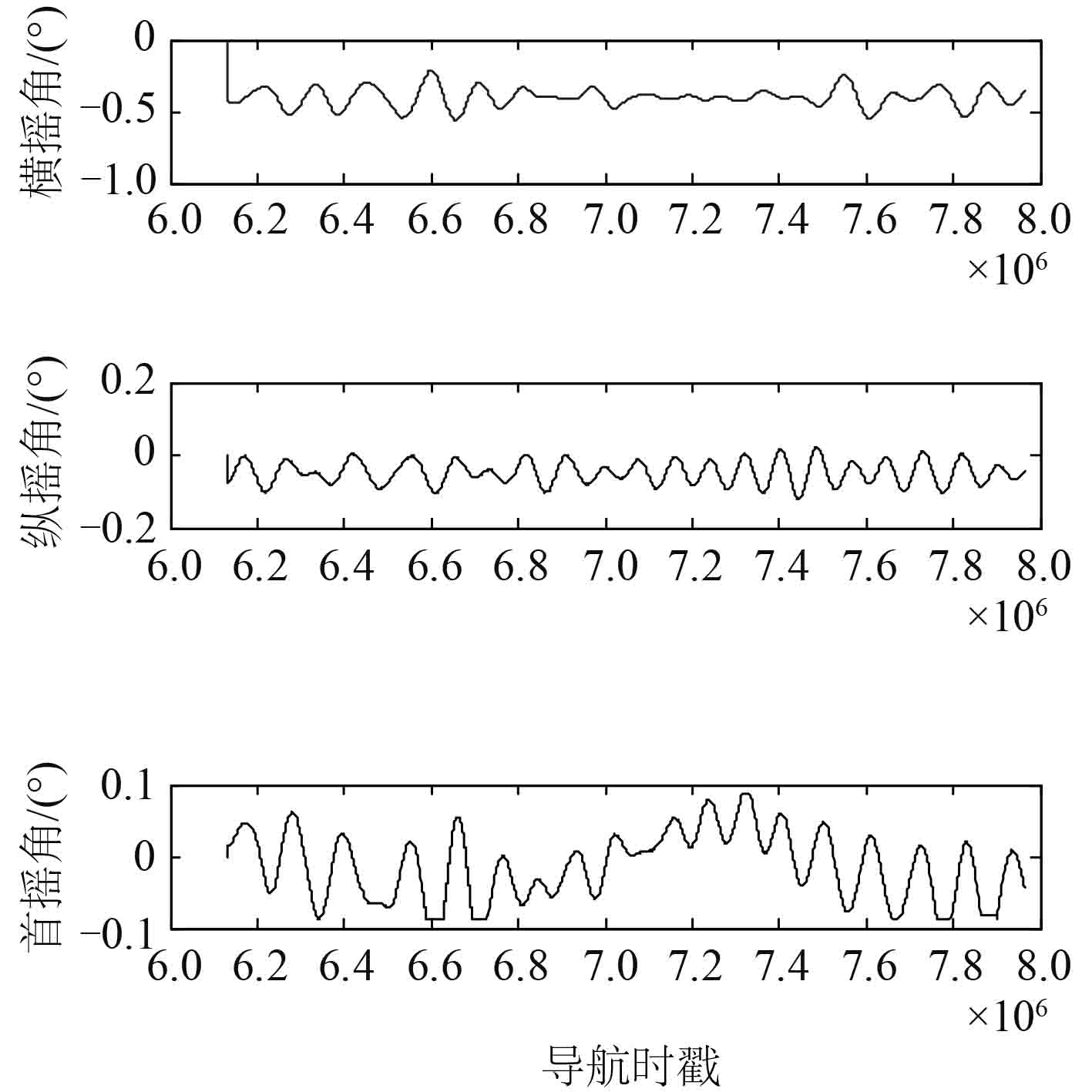
|
图 1 中线电视处船体姿态信息 Fig. 1 The ship attitude information at the centerline camera |
在上述基础上,对着舰引导雷达单站定位、两站联合定位和本文提出的数据融合定位方法进行了 10 000 次蒙特卡洛仿真分析。
设备的测量误差会在模型解算中产生误差传递,在不考虑局部基准测姿误差和各设备位置误差的条件下,传递后的着舰引导雷达距离、角度误差方差变化比如图 2 所示,中线电视的测角误差方差比如图 3 所示。
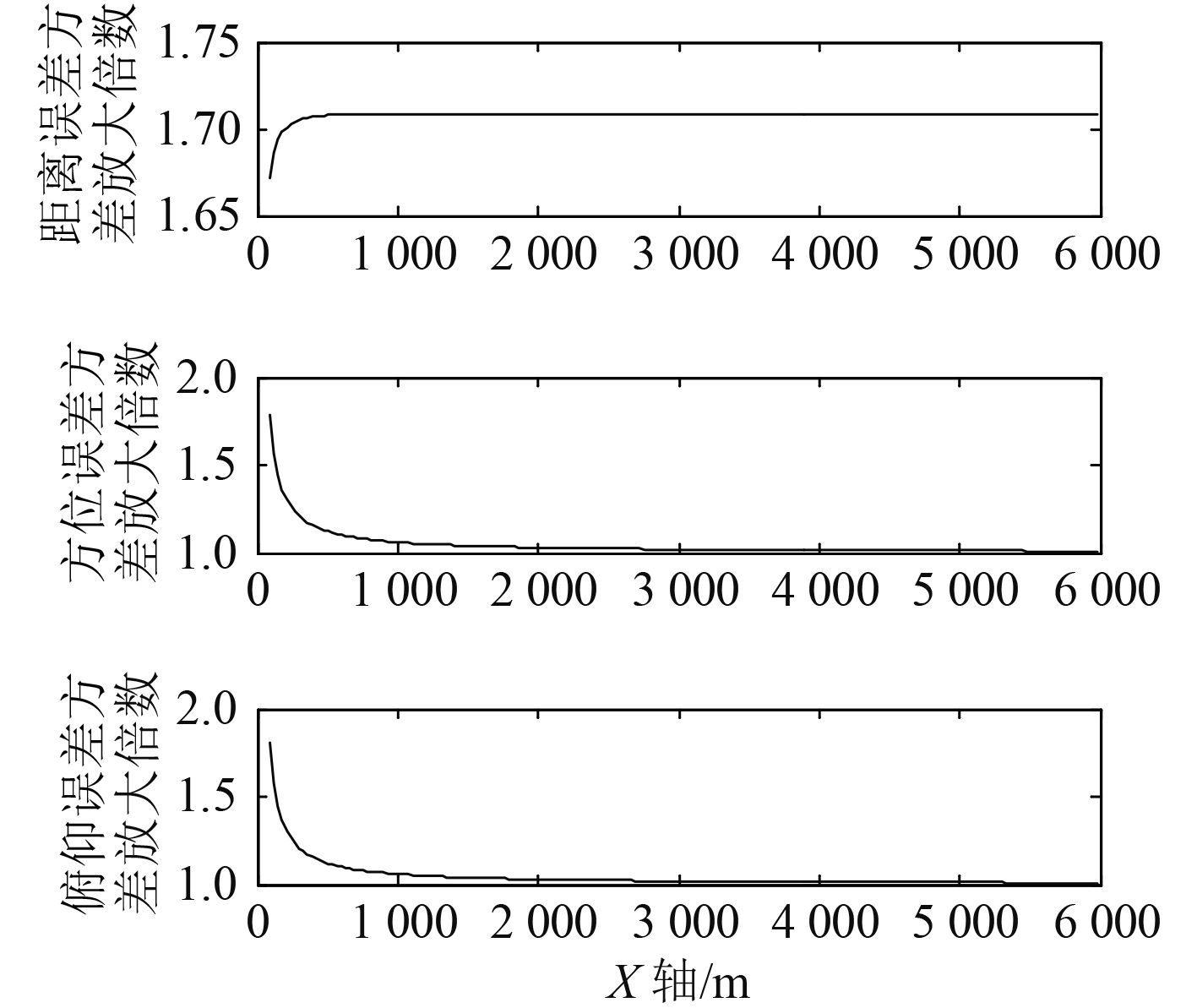
|
图 2 着舰引导雷达测距/测角误差方差放大比例 Fig. 2 The variance amplification ratio of the landing guidance radar ranging and angle measurement error |
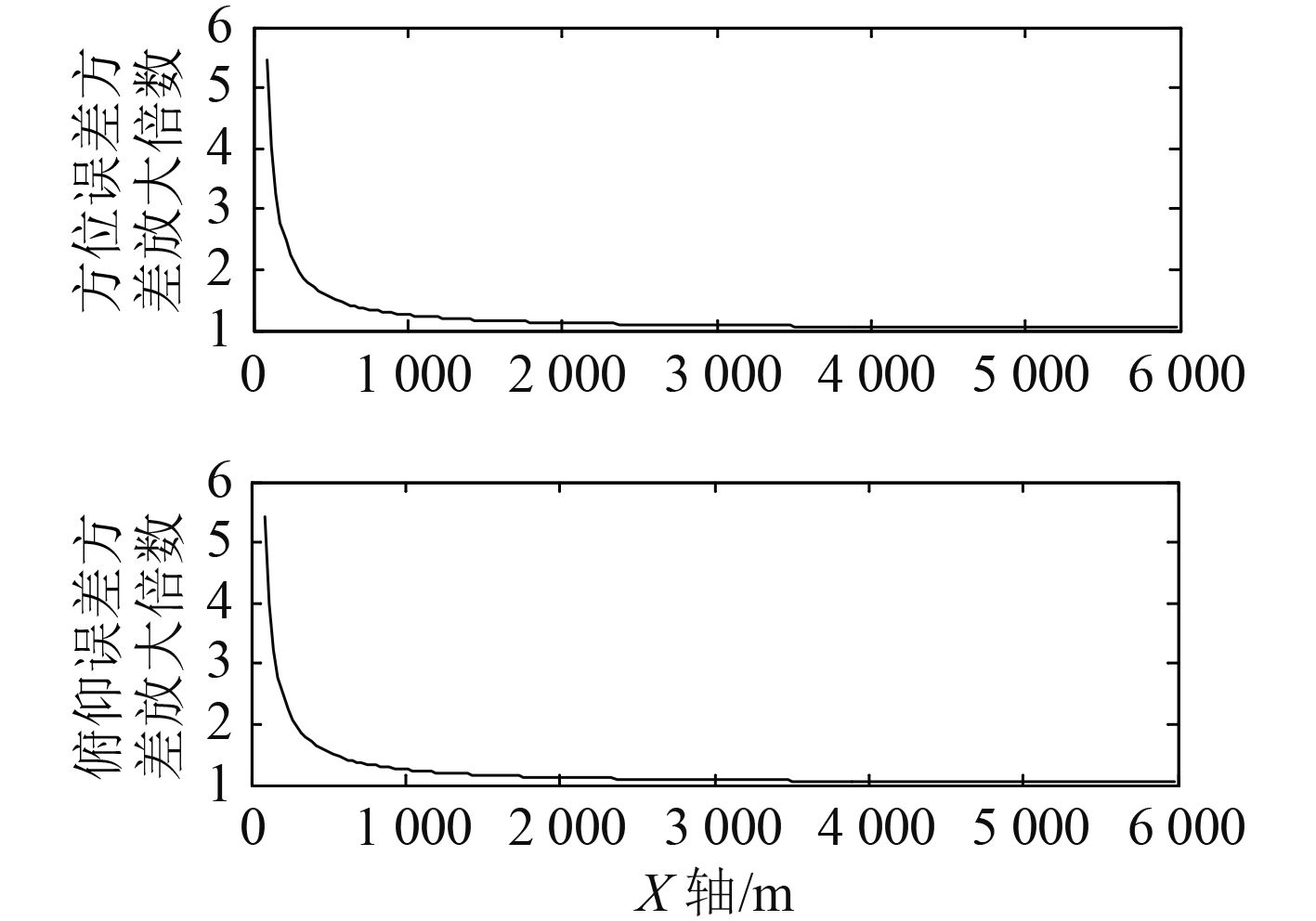
|
图 3 中线电视测角误差方差放大比例 Fig. 3 The variance amplification ratio of the centerline camera angle measurement error |
由图 2和图3 可看出,着舰引导雷达、中线电视测量误差在计算过程中产生的累积程度与目标距理想着舰点的距离有关。着舰引导雷达测距误差引起的距离积误差方差与目标距离成正比,最后放大倍数稳定至 1.7 倍左右,着舰引导雷达、中线电视测角累积误差引起的角度累积误差方差与目标距离成反比,着舰引导雷达测角误差导致的误差方差放大倍数在 2 倍以内,中线电视角误差导致的误差方差放大倍数在目标X 轴坐标值 269 m 处达到 2 倍。
为比较着舰引导雷达单站定位、文献[2]中着舰引导雷达/中线电视两站联合定位及本文提出的数据融合定位算法的定位性能,用均方根误差来对 3 种方法的定位精度进行衡量,在目标着舰过程中 3 种定位方法的定位性能如图 4 所示。
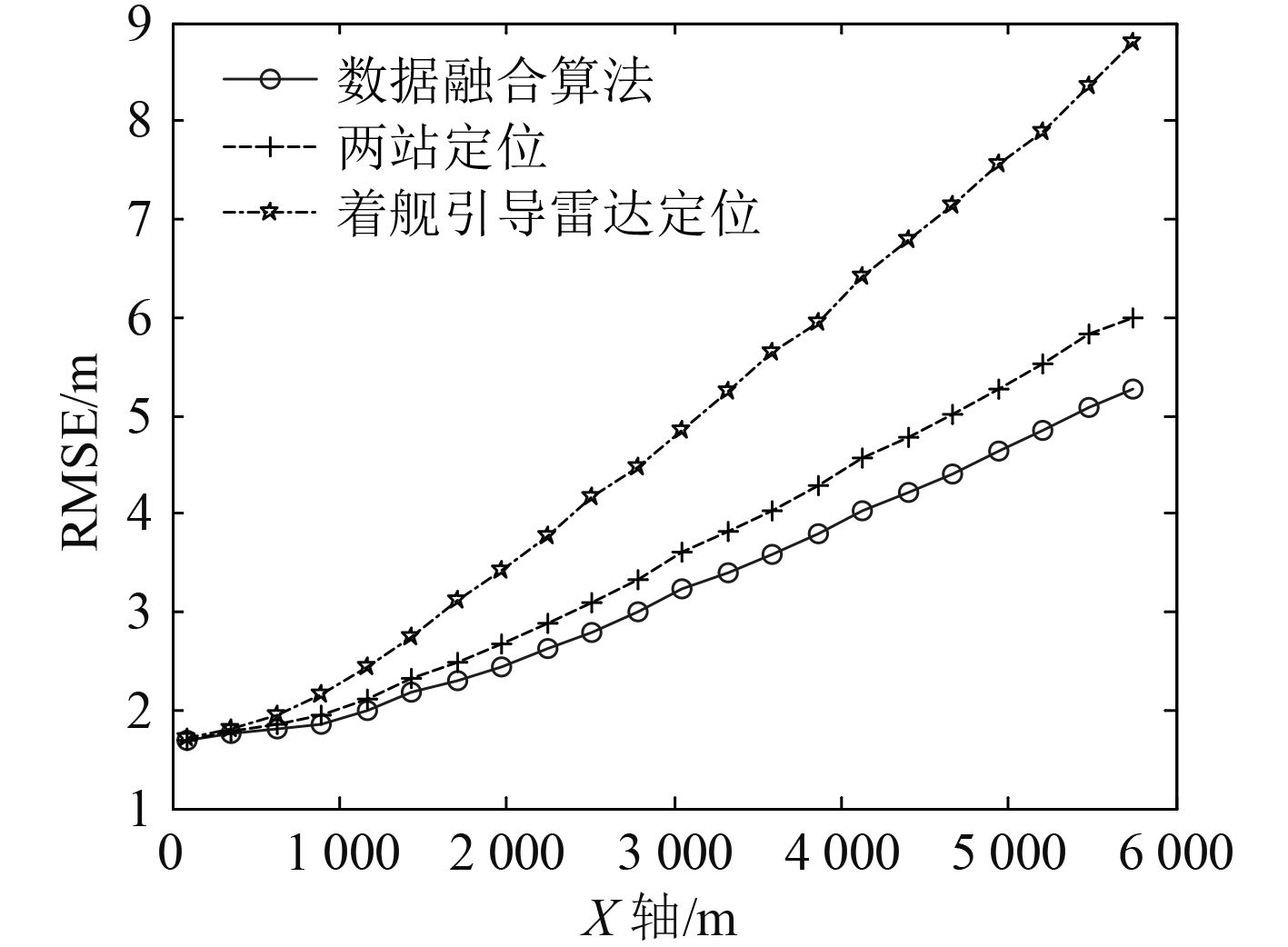
|
图 4 三种定位方法的均方根误差比较 Fig. 4 Comparison of root mean square error of three kinds of positioning methods |
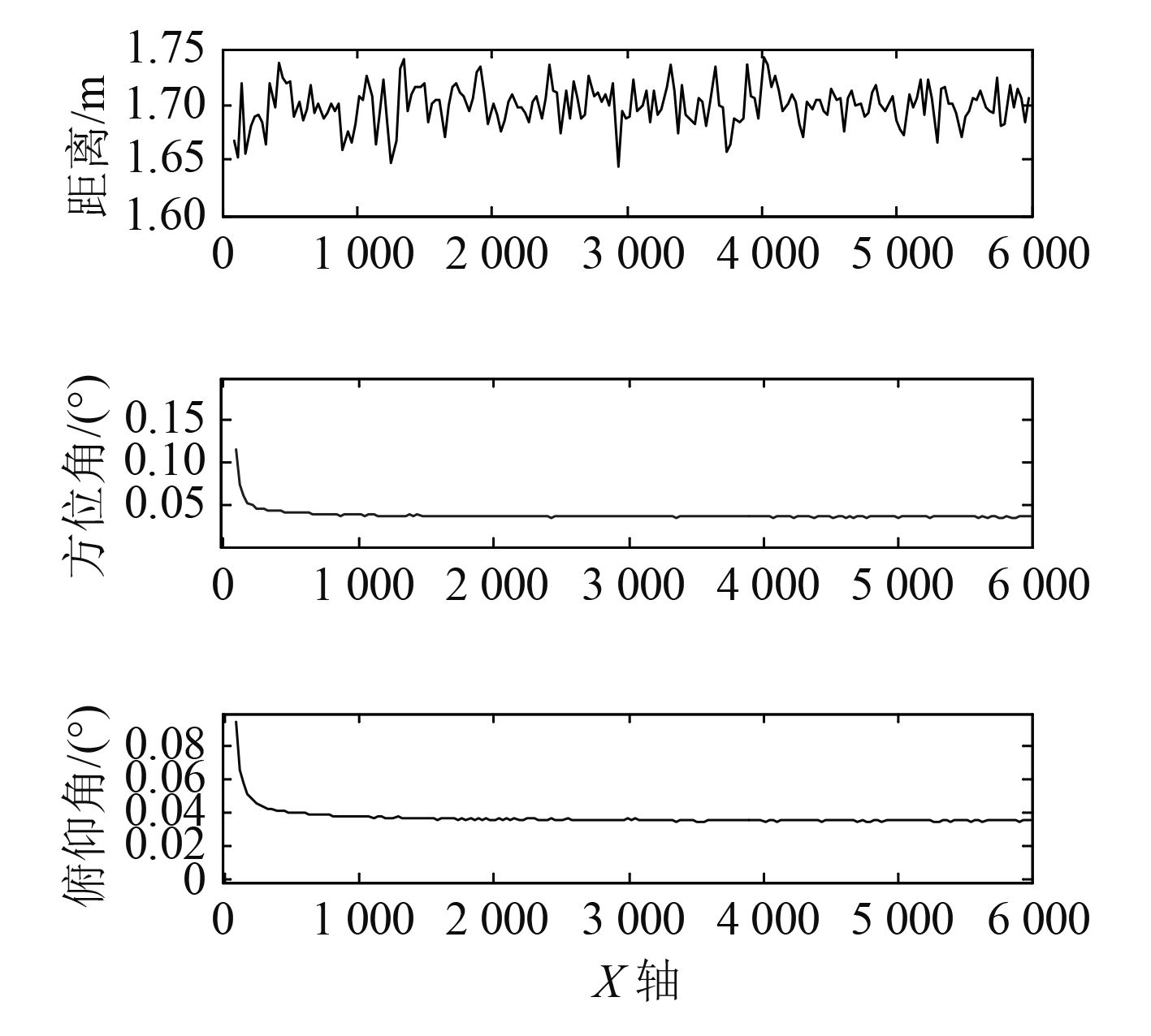
|
图 5 极坐标下的数据融合目标定位性能 Fig. 5 Positioning performance of data fusion target in polar coordinates |
由图 4 可知,3 种定位方法定位精度均与目标离舰的距离成正比;其中着舰引导雷达单站定位性能最弱,本文提出的数据融合定位算法定位精度最高,并且随着目标距离的增加优势逐渐明显,在 6 km 处均方根误差能达到 5 m 以内。
用极坐标的形式来表示本文方法的定位误差特性如图 5 所示。
由图 5 可知,本文提出的方法测距精度在 1.7 m 左右,在目标X 轴坐标大于 500 m 时测角精度低于 0.04°,最后趋近于 0.035° 即测角精度要高于中线电视测角精度,在 500 m 以内,测角精度变差是由于误差累计导致的。
4 结 语由上述仿真可知,本文提出的着舰引导雷达/中线电视数据融合定位算法有较好的定位性能,测角精度可达到 2 mrdd。在工程实践中,真值测量设备的精度要高于被标校设备精度的 3 倍以上方可[10],故若采用着舰引导雷达/中线电视数据融合定位算法作为真值测量手段,被标设备的测距精度和测角精度的临界值分别为 5.1 m和 6 mrdd。本文提出的自标校方案具有一定得理论价值和可行性。
| [1] | PRICKETT A L, PARKES C J. Flight testing of the F/A-18E/F automatic Carrier landing system.[C]//IEEE Proceedings Aerospace Conference. Big Sky, MT, USA:IEEE Press, 2001, 5:2593–2612. |
| [2] | 王兆毅, 刘爱东, 高波, 等. 一种舰载机下滑道一致性指示数据产生方法[J]. 指挥控制与仿真, 2016, 38(2): 84–88. |
| [3] | 柴敏, 于慧, 宋卫红, 等. 光学无线电测量信息融合定位[J]. 光学学报, 2012, 32(12): 1–7. |
| [4] | 石晓荣, 王青, 张明廉, 等. 基于多传感器数据融合的激动目标跟踪自适应算法[J]. 系统仿真学报, 2002, 14(5): 631–636. |
| [5] | 朱志宇. 基于红外和雷达数据融合的激动目标跟踪方法[J]. 激光与红外, 2002, 37(2): 170–174. |
| [6] | 尹继豪, 崔炳喆. 雷达/红外数据融合的机动目标跟踪算法综述[J]. 航空兵器, 2009, 10(5): 39–43. |
| [7] | BLAIR S, ALOUANI A T.A Asynchronous data fision for target tracking with a multi-tasking radar and optical sensor[J]. Acquisition tracking and pointing. SPIEs, 1991, 1482: 234–245. |
| [8] | 梁凯, 潘泉, 宋国明, 等. 基于曲线拟合的多传感器时间对准方法研究[J]. 火力与指挥控制, 2006, 31(12): 51–53. |
| [9] | 王国宏, 毛士艺, 何友. 雷达与红外数据融合算法综述[J]. 火力与指挥控制, 2002, 27(2): 3–6. |
| [10] | 钟德安. 航天测量船测控通信设备标校与校飞技术[M], 北京: 国防工业出版社, 2009. |
 2017, Vol. 39
2017, Vol. 39
