0 引　言

矢量水听器可以同时测量声场的声压和质点振速信息的传感器，通过联合处理声压和振速得到不同的组合指向性，并为最简单的线列阵带来了分辨左/右舷模糊的能力^{[1 –3]}。目前对于矢量线阵的空间谱估计已经有较多的文献发表，而对于矢量圆阵的研究较少^{[4 –6]}。圆阵和直线阵相比有诸多优点，可以进行 360°无模糊测向。在矢量线阵空间谱估计研究方面，文献[7]提出了 VTAMVDR（MVDR based on Time-domain Aanalysis signals of Vector Sensor）空间谱估计方法，VTAMVDR 的基本思想是应用 TAMVDR（MVDR based on Time-domain Aanalysis signals）的理念将接收到的声压振速时域实数信号通过希尔伯特变换构造出复数形式的解析信号，再利用线性约束条件使阵列输出功率最小的准则确定复数形式的最优权向量，从而获得来波方向的波束输出功率。在构造时域解析信号的基础上，对每一路时域解析信号引入复权，利用期望方向的输出相应不变的约束使阵列输出功率最小而获得权向量的最优解。利用 TAMVDR，可在单次快拍下获得稳定优化解，信号检测和方位分辨性能较优。相对于其他算法需要很多快拍数据才能收敛而言，该算法相对降低了对条件的依赖，同时运算量相对较小。本文研究了 VTAMVDR 在矢量圆阵中的应用。首先从矢量圆阵的阵列模型出发，提出了矢量圆阵时域解析 MVDR 算法，研究了矢量圆阵时域解析 MVDR 算法原理及实现流程，然后通过仿真分析对比了矢量圆阵时域解析 MVDR 算法与矢量圆阵常规波束形成的波束宽度和分辨率。

1 矢量圆阵时域解析 MVDR 算法原理

图 1 给出了一个在圆周上均匀分布的平面离散圆阵图，设离散圆阵的半径为r，阵元为N 个二维矢量水听器，把时间的参考点选在圆心O 上，设入射信号来自 0°方向，相邻 2 个阵元的夹角为 $\alpha = 2\pi /N$ ，假设圆阵每次波束扫描时，有 2M 个基元参与工作，记 2M 个矢量水听器p，v_x ，v_y 接收信号经时延 $\Delta {\tau _i}{\rm{ }}( - M \leqslant i \leqslant M)$ 以及滤波之后的输入信号分别为：

$\left\{ \begin{array}{l}P = S{}_p + {V_p}\text{，}\\{V_x} = S{}_x + {V_x}\text{，}\\{V_y} = S{}_y + {V_y}\text{。}\end{array} \right.$

(1)

式中：S_p ，S_x ，S_y 为期望目标信号矢量；V_p ，V_p ，V_y 为阵列加性各向同性噪声矢量与干扰之和。

利用 Hilbert 变换 $H( \cdot )$ 构造时域复数信号为：

$\left\{ \begin{array}{l}{Y_P} = P + j \cdot H(P)\text{，}\\{Y_{{V_x}}} = {V_x} + j \cdot H({V_x})\text{，}\\{Y_{{V_y}}} = {V_y} + j \cdot H({V_y})\text{。}\end{array} \right.$

(2)

阵列输出功率为：

$P = E[{ Y}{{ Y}^{H}}] = {{w}^{H}}{{R}_c}{w} \text{，}$

(3)

式中

${ Y} = \left[ \begin{array}{l}{Y_P}\\{Y_{{V_x}}}\\{Y_{{V_y}}}\end{array} \right]\text{。}$

对权向量的求解可以表述为有约束的优化问题：

$\left\{ \begin{array}{l}\arg \underbrace {\min }_w({{w}^H}{{R}_c}{w})\text{，}\\{\rm s}.{\rm t}. {{w}^H}\left[ {{A} \otimes a\left( \theta \right)} \right] = 1\text{。}\end{array} \right.$

(4)

式中： ${A} = {\left[ {1,1, \cdots ,1} \right]^{\rm T}}$ 为 2M 个 1 组成的列矩阵； $\theta $ 为扫描方位。

先构造1个代价函数：

$L(w) = \frac{1}{2}{{w}^{H}}{{R}_c}{w} - \lambda \left\{ {{{w}^{H}}\left[ {{A} \otimes a\left( \theta \right)} \right] - 1} \right\} \text{，}$

(5)

上式对 ${w}$ 求导，并令导数为0，得到：

${w} = \lambda \left[ {{A} \otimes a\left( \theta \right)} \right]{{R}_c}^{^{ - 1}}\text{。}$

(6)

根据约束条件 ${{w}^{H}}\left[ {{A} \otimes a\left( \theta \right)} \right] = 1$ 可以求得矢量圆阵时域解析 MVDR 算法的最优权向量为：

${w} = \frac{{{{\left[ {{A} \otimes a\left( \theta \right)} \right]}^{H}}{{R}_c}^{ - 1}}}{{{{\left[ {{A} \otimes a\left( \theta \right)} \right]}^{H}}{{R}_c}^{ - 1}\left[ {{A} \otimes a\left( \theta \right)} \right]}} \text{，}$

(7)

其输出功率为：

$P(\theta ) = \frac{1}{{{{\left[ {{A} \otimes a\left( \theta \right)} \right]}^H}{{R}_c}^{ - 1}\left[ {{A} \otimes a\left( \theta \right)} \right]}}\text{。}$

(8)

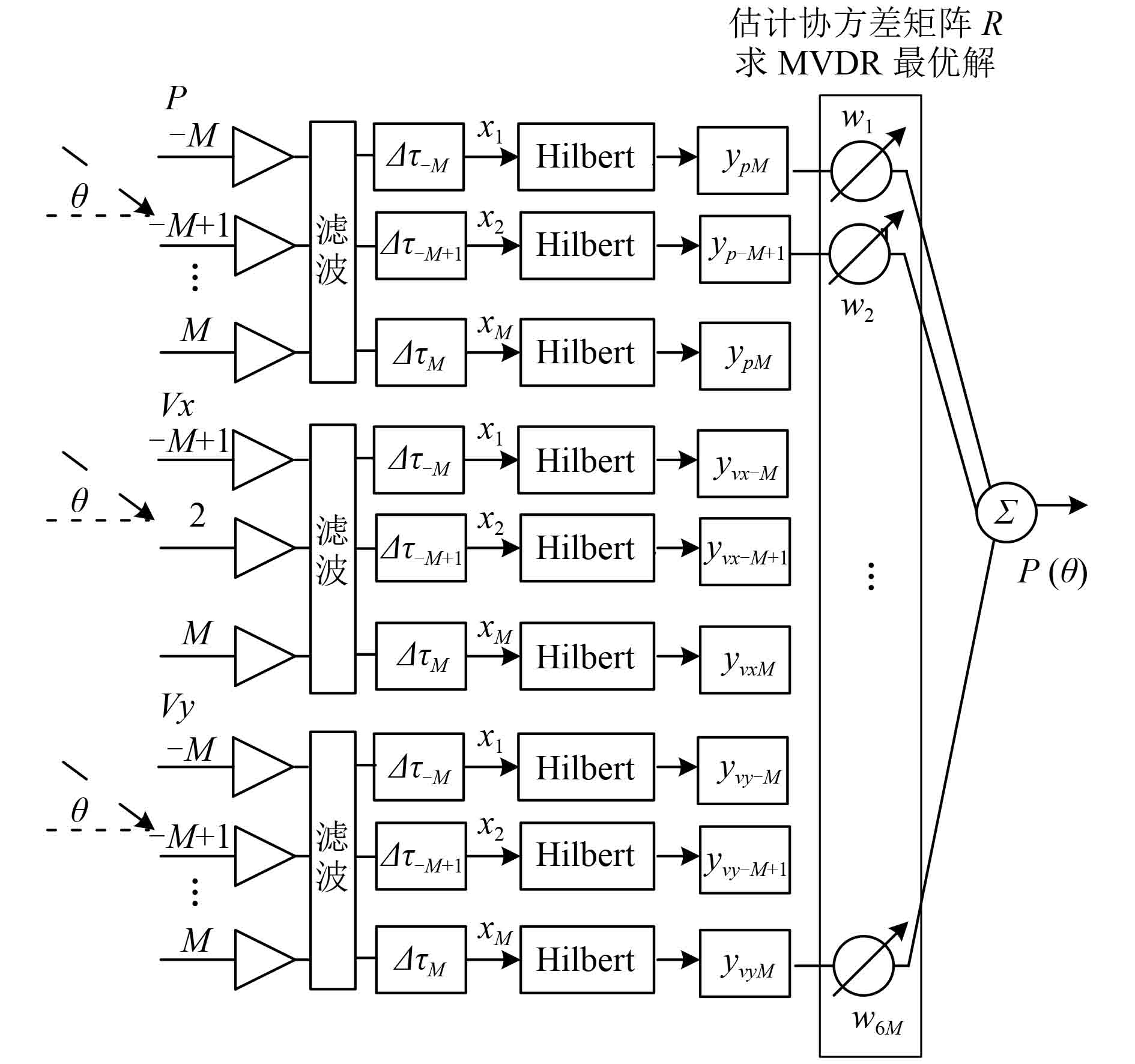
图 2 给出了矢量圆阵时域解析自适应波束形成流程图。

从图 2 可看出，矢量圆阵时域解析 MVDR 完全基于时域处理，在数据长度满足条件时，一般只需要1次快拍，不需要进行子带分解，减小了计算量。当阵元个数较多时，能大大减小运算量，方便使用 DSP 实现矢量水听器阵列的工程化应用。

2 数值仿真分析

均匀圆阵，半径为 0.8 m，由 32 个矢量水听器阵元组成，采样率为 40 kHz，处理频带范围 [2 kHz，4 kHz]，1次快拍点数为 1 024 点，目标在观测时间内方位不变，信噪比为 5 dB，加性噪声为高斯白噪声，采用一次快拍，目标在观测时间内方位不变，加性噪声为高斯白噪声。考察矢量圆阵常规波束形成和矢量圆阵时域解析自适应波束形成多次方位估计的均方根误差（root mean square error, RMSE）^[8]。

定义N 次目标方位估计的 RMSE 为：

$\sqrt {\frac{1}{N}\sum\limits_{j = 1}^N {\left( {{{\bar \theta }_{ij}} - {\theta _{ij}}} \right)} {}^2} \text{。}$

(9)

其中 ${\theta _{ij}}$ 和 ${\bar \theta _{ij}}$ 分别为第i 个目标第j 次试验的真值和估计值。

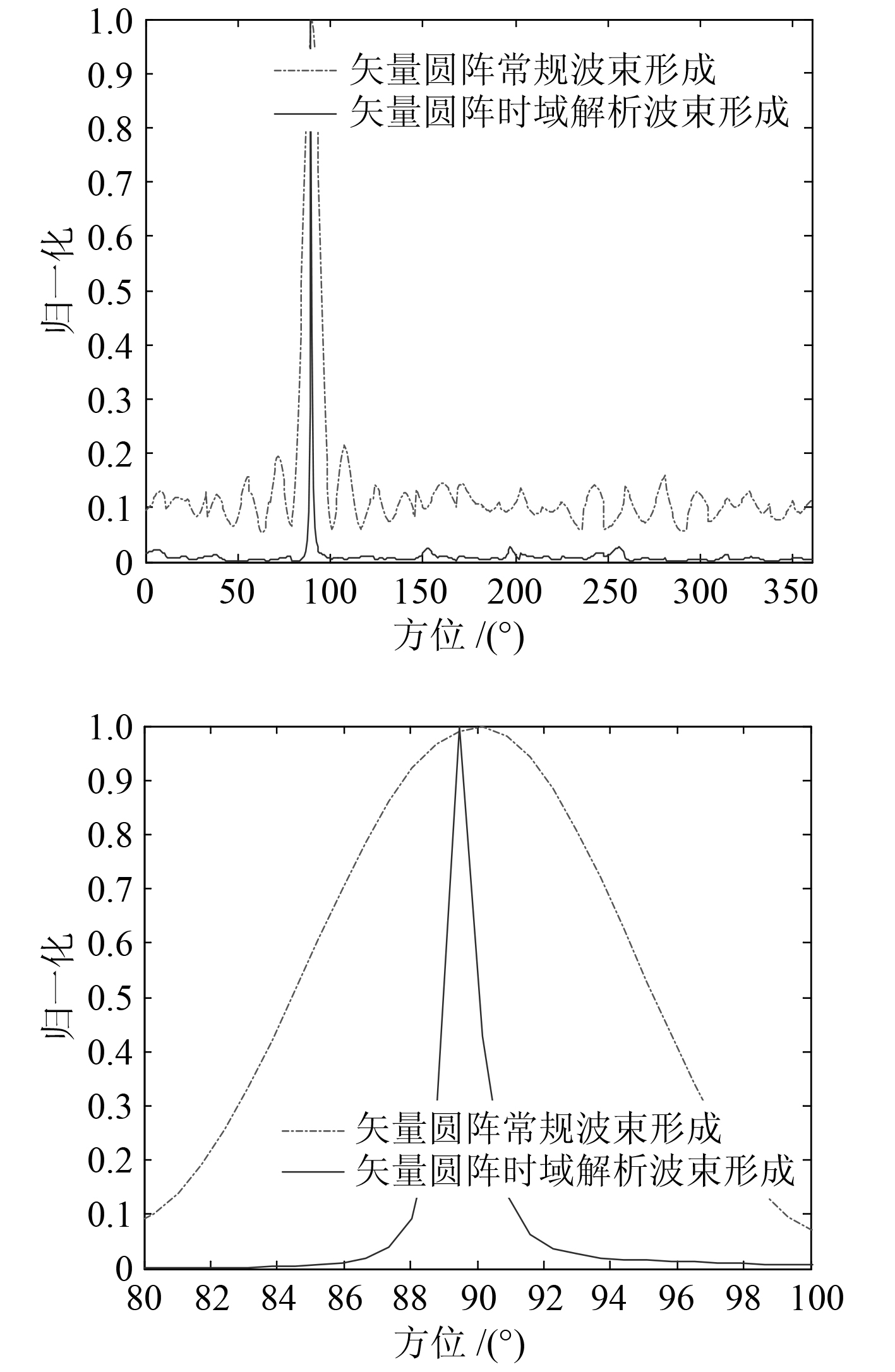
图 3 给出了单目标条件下矢量圆阵常规波束形成和矢量圆阵时域解析MVDR算法的波束输出对比。

从图 3 可看出，矢量圆阵常规波束形成下降 3 dB，波束宽度为 10.87°，本文提出的矢量圆阵时域解析 MVDR 算法为 1.11°，明显波束宽度较窄，本文算法的波束宽度为常规波束形成的 10.21%。

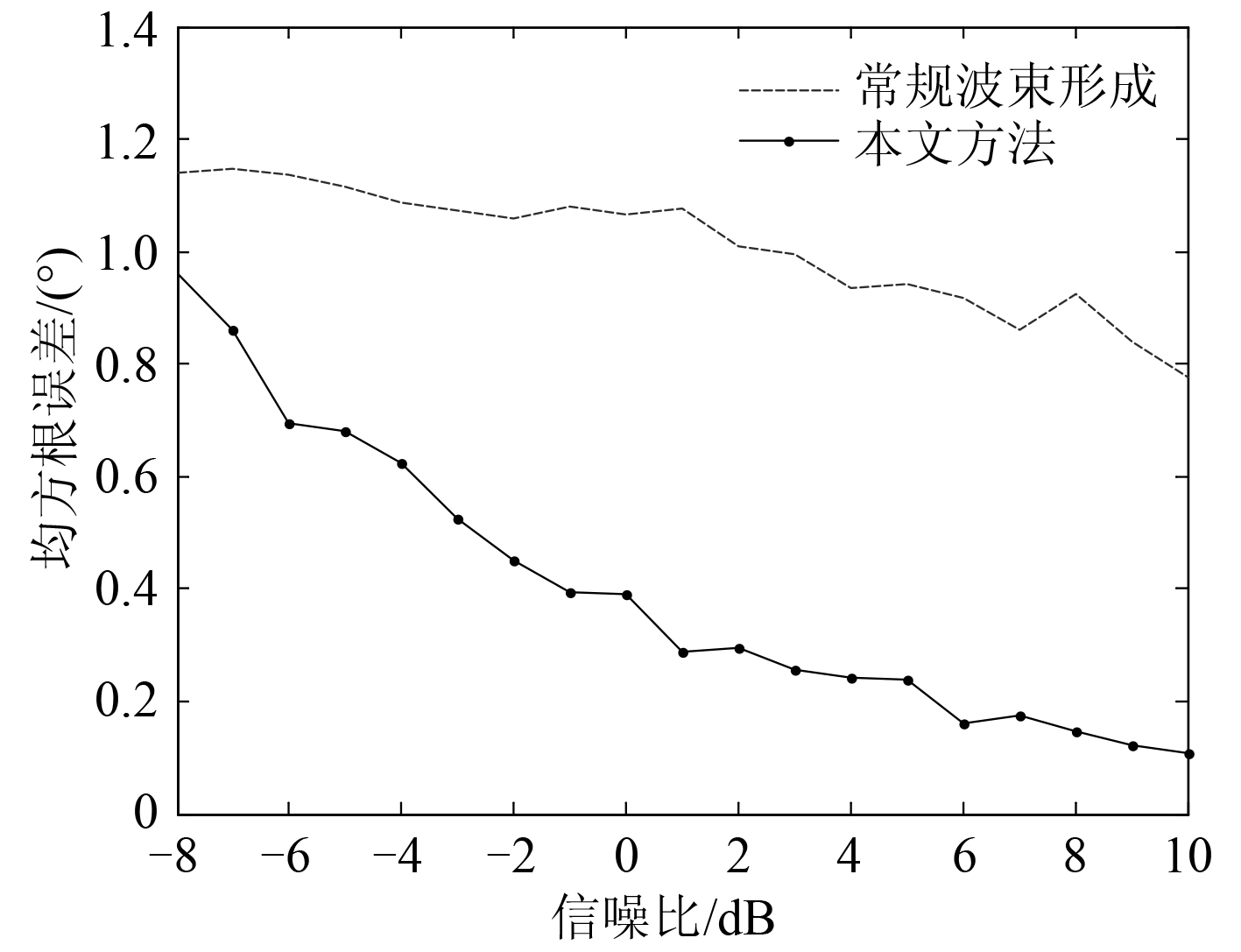
图 4 给出了 2 种方法 RMSE 随信噪比变化示意图，可以看出随着信噪比的变化，矢量圆阵常规波束形成方法的性能弱于矢量圆阵时域解析 MVDR 算法。

仿真条件不变，有 2 个宽带信号入射，分别位于 90°和 98°方位，目标在观测时间内方位不变，信噪比为 5 dB，加性噪声为高斯白噪声，假设估计的两目标方位为 ${\bar \theta _1}$ 和 ${\bar \theta _2}$ ，如果满足下式：

$\left| {{{\bar \theta }_1} - {\theta _1}} \right| - \left| {{{\bar \theta }_2} - {\theta _2}} \right| < \left| {{{\bar \theta }_1} - {{\bar \theta }_2}} \right|\text{。}$

(10)

则认为是一次成功双目标分辨。

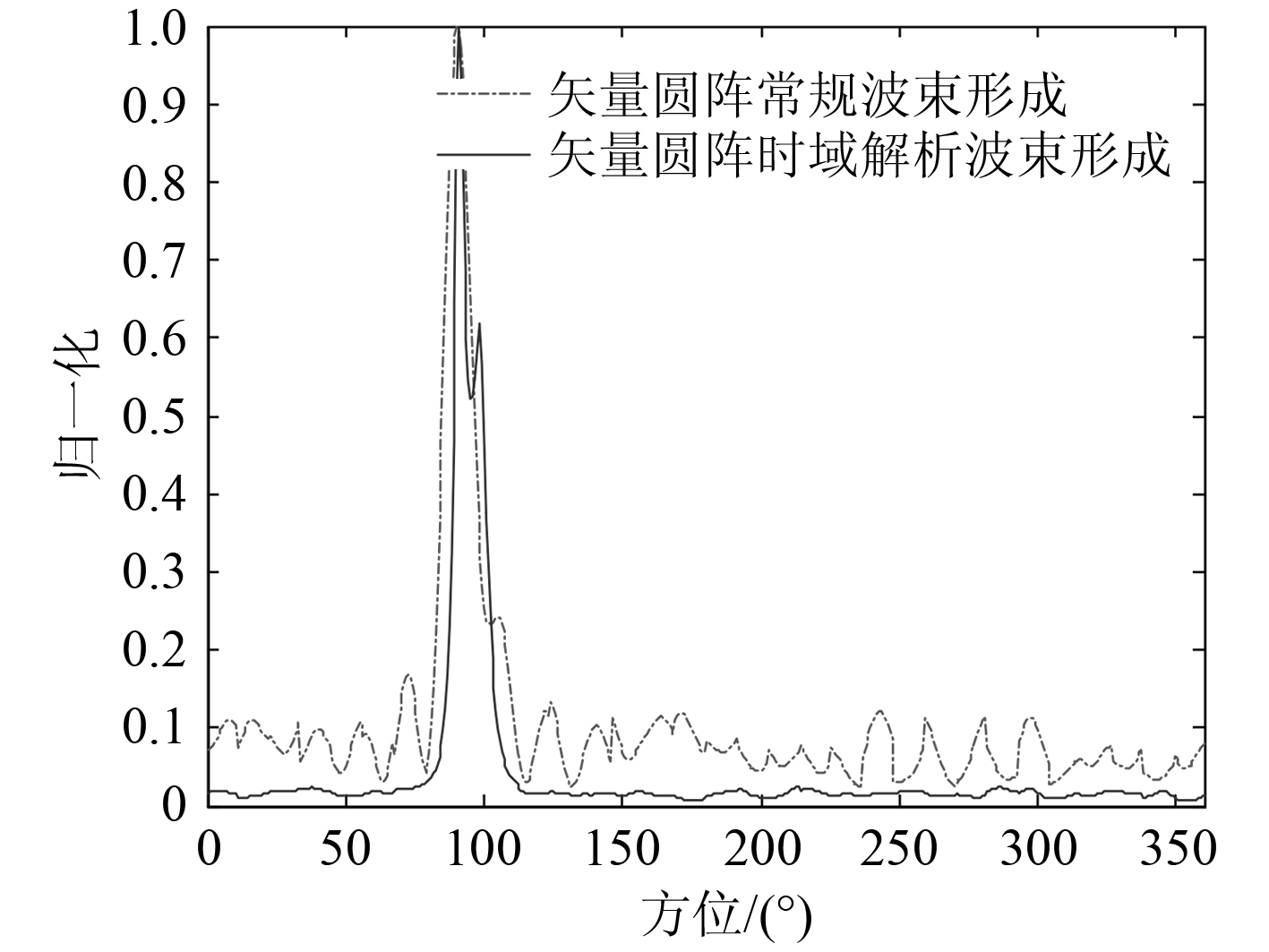
图 5 给出了双目标条件下矢量圆阵常规波束形成和矢量圆阵时域解析自适应波束形成的波束输出，可以看出矢量圆阵时域解析自适应波束形成可以明显的分辨 2 个目标而常规波束形成不能分辨。

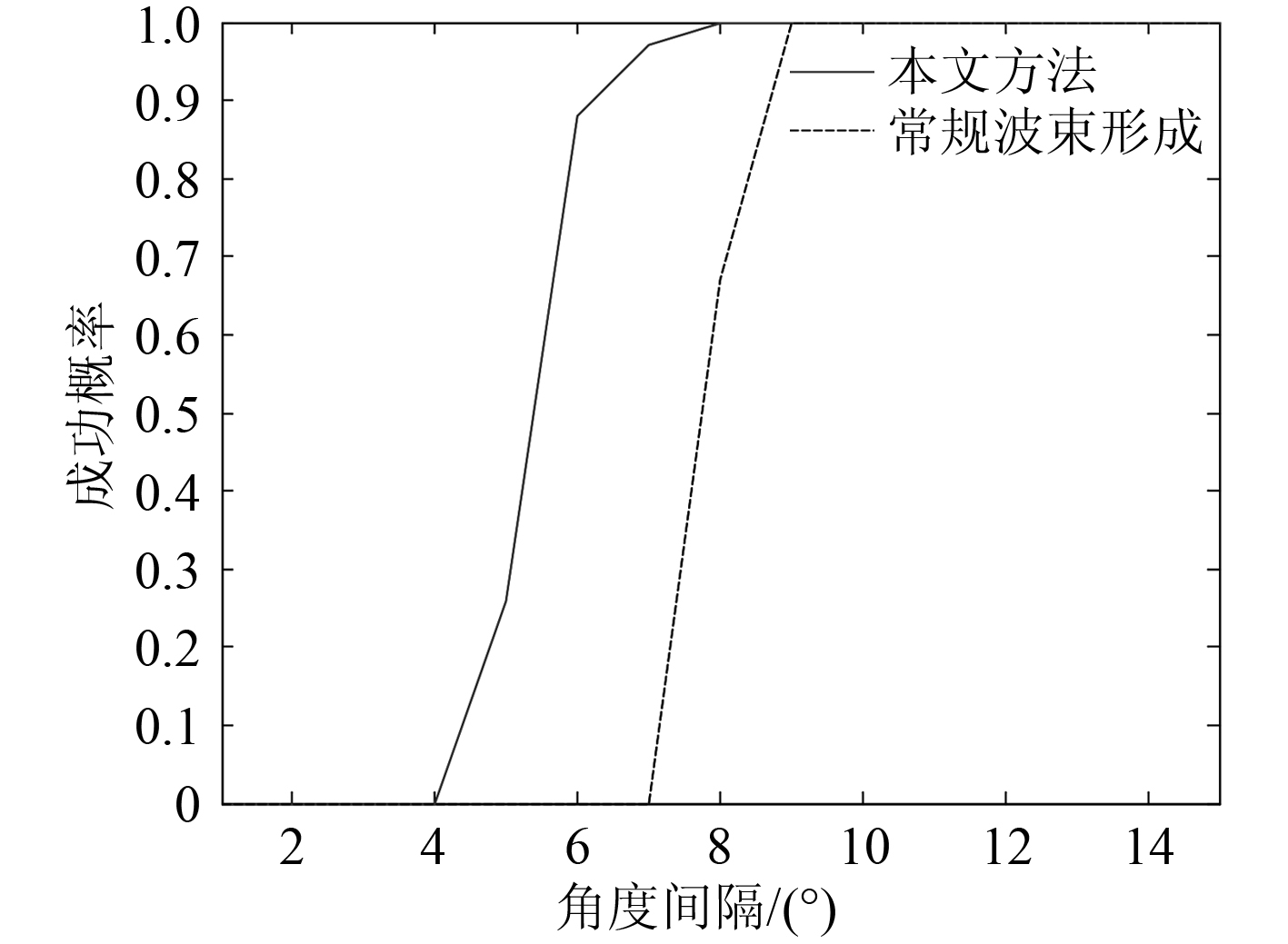
图 6 给出了不同角度间隔下 2 种方法的分辨能力对比图，可以看出本文方法与常规波束形成方法相比分辨性能较优。

3 结　语

本文提出了矢量圆阵时域解析 MVDR 算法，理论和仿真分析了本文方法的性能，通过和常规波束形成进行对比，可以看出本文方法在方位估计性能和目标分辨能力上明显优于常规波束形成，具有较高的估计精度，较低的双目标分辨门限。