0 引　言

水下拖曳线列阵是由一组换能器串联而成的水听器阵列。在水下航行器尾部挂载一段拖曳线列阵，可极大地提高其水下探测能力；在水下模拟靶标尾部挂载拖曳线列阵，模拟潜艇等大目标的线尺度亮点声学特性。因此在水下探测、反鱼雷技术和鱼雷靶标等领域中，水下拖曳线列阵的应用前景广阔。

目前，国内外关于水下拖曳系统的研究主要集中在对均质圆截面缆（即水下拖缆）的动力学特性仿真及试验研究^{[1 –6]}，而很少有关于非均质线列阵拖缆的研究。在实际应用中的线列阵，由于安装有换能器，属于典型非均质型拖缆。本文根据非均质线列阵结构特性，在研究时将其分段处理，转化成分段均质拖缆，最后组合得到完整的线列阵拖缆模型。基于 Matlab，建立了线列阵空间运动模型，发展一套线列阵动力学特性数值仿真程序，分析其动力学特性，设计并开展线列阵拖曳试验对仿真结果进行验证，最终建立有效可靠的线列阵等非均质拖缆动力学特性分析方法。

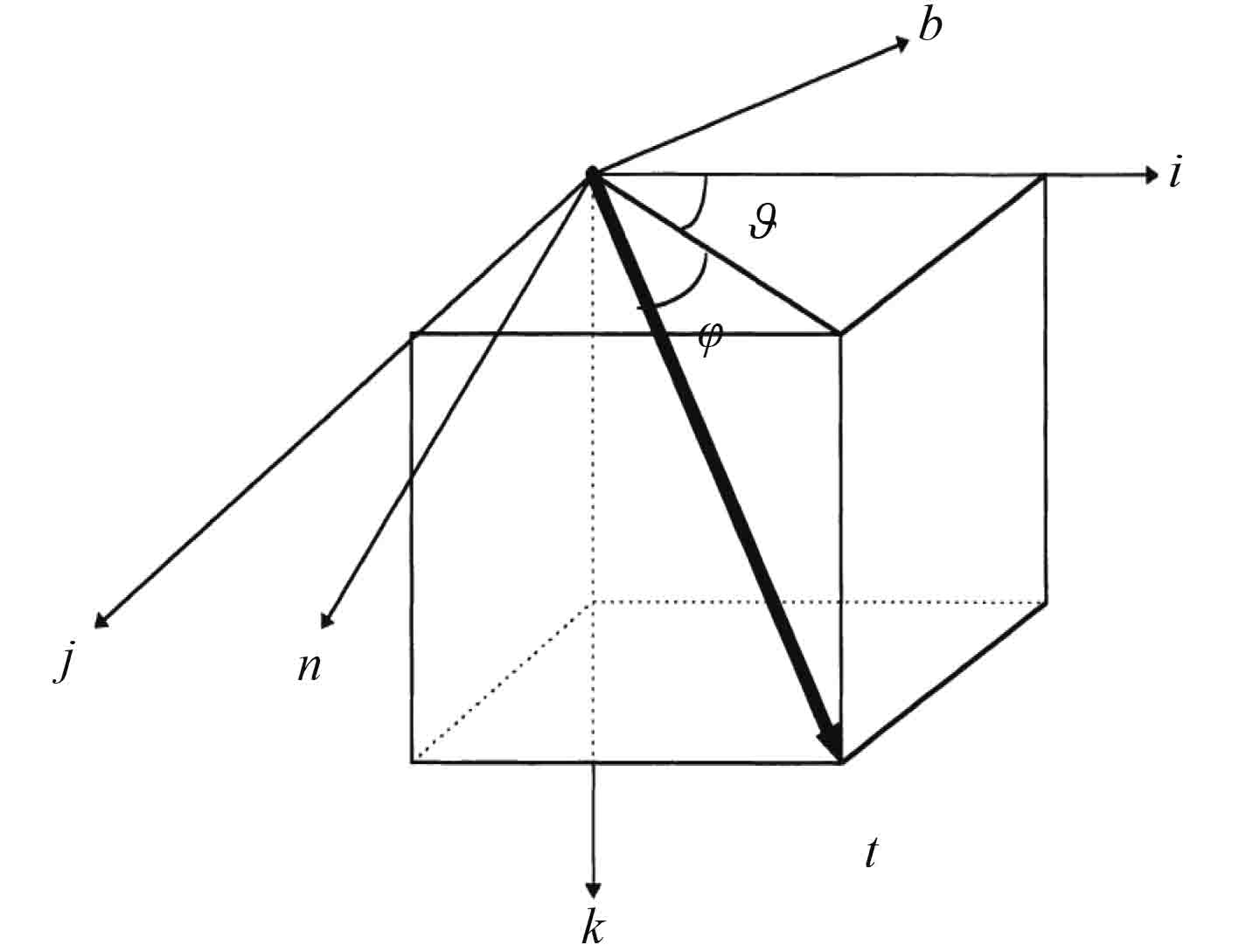
1 线列阵拖缆动力学仿真 1.1 拖缆仿真模型建立

由于拖缆所受水动力项更易被表示为在局部自然坐标系下各分量方向上的分力，因此，建立如图 1 所示坐标系^[7]。其中惯性系 $O - \xi \eta \zeta $ 与拖曳载体固连，其单位矢量以 $(\vec { i},\vec { j},\vec { k})$ 表示；局部系 $B - xyz$ 原点位于拖缆上， $t,n$ 分别为沿拖缆上任一点处的切向和法向，b 按右手直角坐标系确定，其单位矢量以 $(\vec t,\vec n,\vec b)$ 表示。惯性系通过 3 次旋转可以与局部系重合，之间的欧拉角为 $(\theta ,\varphi )$ 。

在对拖缆进行分析中，忽略拖缆弯曲应力和海流的影响，只需要确定 6 个变量就能描述整个系统，这 6 个变量分别为T，V_t ，V_n ，V_b ， $\theta $ ， $\varphi $ 。分别对拖缆的动力平衡及运动平衡进行分析，最终得到拖缆的平衡方程。经过整理得到如下矩阵形式：

$ { M}\vec { y}' = { N}\dot {\vec { y}} + {q}{\text{，}}$

(1)

其中：

$\vec { y} = \left( {T,{V_t},{V_n},{V_b},\theta ,\varphi } \right),$

${ M} \!=\! \left[\!\! {\begin{array}{*{20}{c}}1&0&0&0&0&0\\0&1&0&0&{ - {V_b}\cos \varphi }&{ - {V_{\rm{n}}}}\\0&0&1&0&{ - {V_b}\sin \varphi }&{{V_t}}\\0&0&0&1&{{V_t}\cos \varphi + {V_n}\sin \varphi }&0\\0&0&0&0&{T\cos \varphi }&0\\0&0&0&0&0&T\end{array}}\!\! \right],$

${{N}} \!=\! \left[ \!\!{\begin{array}{*{20}{c}}{ \!-\! \frac{{em{V_{\rm{t}}}}}{{1 + eT}}}\!&\!m\!&\!0\!&\!0\!&\!{ - {m_1}{V_b}\cos \varphi }\!&\!{{m_1}{V_n}}\\e\!&\!0\!&\!0\!&\!0\!&\!0\!&\!0\!\\0\!&\!0\!&\!0\!&\!0\!&\!0\!&\!{1 + eT}\\0\!&\!0\!&\!0\!&\!0\!&\!{\left( {1 + eT} \right)\cos \varphi }\!&\!0\\{ \!-\! \frac{{e{m_1}{V_b}}}{{1 + eT}}}\!&\!0\!&\!0\!&\!{{m_1}}\!&\!{{m_1}{V_n}\sin \varphi + m{V_t}\cos \varphi }\!&\!0\\{ \!-\! \frac{{e{m_1}{V_n}}}{{1 \!+\! eT}}}\!&\!0\!&\!{{m_1}}\!&\!0\!&\!{ - {m_1}{V_b}\sin \varphi }\!&\!{m{V_t}}\end{array}}\!\! \right],$

${ q} \!=\! \left[\!\! {\begin{array}{*{20}{c}}{ - w\sin \varphi + \frac{1}{2}\rho d{{\left( {1 + \varepsilon } \right)}^{\frac{1}{2}}}\pi {C_t}{U_t}\left| {{U_t}} \right|}\\0\\0\\0\\{\frac{1}{2}\rho d{{\left( {1 + \varepsilon } \right)}^{\frac{1}{2}}}\pi {C_n}{U_b}{{\left( {{U_{\rm{b}}}^2 + {U_n}^2} \right)}^{\frac{1}{2}}}}\\{w\cos \varphi + \frac{1}{2}\rho d{{\left( {1 + \varepsilon } \right)}^{\frac{1}{2}}}{C_n}{U_n}{{\left( {{U_{{b}}}^2 + {U_n}^2} \right)}^{\frac{1}{2}}}}\end{array}} \!\!\right]\text{。}$

式中： $\varepsilon = eT$ ， ${\rm{e}} = 1/EA$ ，E 为缆的杨氏模量，A 为未伸长缆绳的截面积；m 为单位长度缆的质量； $\rho $ 为海水密度； ${m_1} = m + \rho A$ ；d 为缆伸长后的直径； $\vec { U}\left( {{U_t},{U_n},{U_b}} \right)$ 为拖缆上任意点相对水流的速度； ${C_t}$ 和 ${C_n}$ 分别为拖缆的切向与法向阻力系数。

为求解该非线性方程组，还需要确定其边界条件。边界条件分为上端点边界条件和下端点边界条件，具体如下：

1）拖缆上端点边界条件

拖缆上端点与拖曳载体连接，属于固定拖点，其速度与拖点的速度相同，得到拖缆上端点 3 个边界条件如下：

$\left\{ \begin{array}{l}{V_t} = {V_i}\cos \theta \cos \varphi - {V_j}\sin \theta \cos \varphi + {V_k}\sin \varphi{\text{，}} \\{V_n} = {V_i}\cos \theta \sin \varphi - {V_j}\sin \theta \sin \varphi - {V_{\rm{k}}}\cos \varphi {\text{，}}\\{V_b} = {V_i}\sin \varphi - {V_j}\cos \theta {\text{。}}\end{array} \right.$

(2)

式中：V_i ，V_j ，V_k 为拖曳载体在惯性系 3 个坐标轴 $\xi $ ， $\eta $ ， $\zeta $ 方向上的速度分量；V_t ，V_n ，V_b 为拖缆拖点处在局部系 3 个坐标轴x，y，z 方向上的速度分量。

2）拖缆下端点边界条件

拖缆下端点没有拖体连接，因此属于自由尾端，张力T 为 0。另外欧拉角 $\theta $ ， $\varphi $ 对弧长s 的变化率为 0，从而得到拖缆下端点 3 个边界条件如下：

$\left\{ \begin{array}{l}T = 0{\text{，}}\\ - w\cos \varphi - \frac{1}{2}\rho d{\left( {1 + \varepsilon } \right)^{\frac{1}{2}}}{C_n}{U_n}{\left( {{U_n}^2 + {U_b}^2} \right)^{\frac{1}{2}}}=\\ {m_1}{{\dot V}_n} + m{V_t}\dot \varphi - {m_1}{V_b}\dot \theta \sin \varphi{\text{，}} \\ - \frac{1}{2}\rho d{\left( {1 + \varepsilon } \right)^{\frac{1}{2}}}{C_n}{U_b}{\left( {{U_n}^2 + {U_b}^2} \right)^{\frac{1}{2}}}=\\ {m_1}{{\dot V}_b} + m{V_t}\dot \theta \cos \varphi + {m_1}{V_n}\dot \theta \sin \varphi {\text{。}}\end{array} \right.$

(3)

1.2 动力学仿真计算

本文研究的对象为拖曳线列阵，如图 2 所示。线列阵全长 110 m，直径 15 mm，总重 48 kg。线列阵由一系列纺锤形的换能器（硫化处理后）和浮子组成，整个线列阵在水中呈零浮力状态。换能器和浮子外径为 82 mm，长度 263 mm，完整的线列阵外形呈“糖葫芦”状。将其分为 14 小段，每一小段又由 7 小节组成，包含一个换能器，与换能器相距 1 m 处有 2 个浮子，在首尾两端各有 2.55 m 长的水密电缆。水中线列阵整体为零浮力状态，据此得到每一分段单位长度线列阵在水中的重力。其阻力系数采用工程估算公式得到，因为线列阵拖缆在水中为零浮力，故在仿真时将其阻力系数简化为定值。线列阵拖缆的计算参数如表 1 所示。

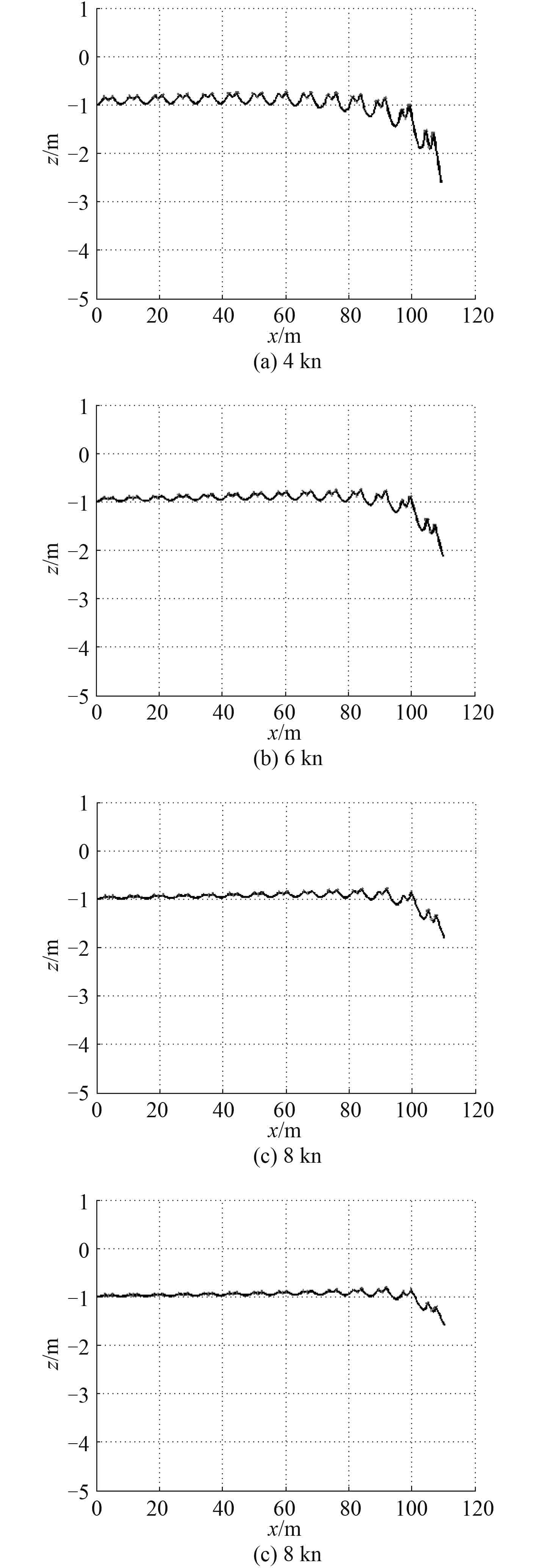
采用中心差分法对拖缆平衡方程式（1）进行离散，使用牛顿迭代法进行时间和空间上的同时迭代求解。编写相应 Matlab 程序，并将表 1 中的参数带入进行仿真计算。在程序中，将 14 小段进行组合得到完整的线列阵模型，仿真得到 4，6，8，10 kn 航速时，拖点位于水下 1 m 深处的拖曳线列阵运动姿态及其阻力，即线列阵拖缆拖点处拉力，具体如图 3 与表 2 所示。

图 3 中，横坐标x 表示航行方向，纵坐标z 表示航行深度。每段中向上突起的点为浮子，向下突出的点为换能器，之间用水密电缆连接。在水中，线列阵拖缆的姿态总体起伏不大，尾部因为没有浮子，缆绳在自身重力的作用下下沉比较明显。为了保证整体的平整性，可考虑在线列阵拖缆尾部增加一段零浮力的尾绳，从而使得其尾部保持较平直状态。

由图 3 可看出，在 10 kn 航速下，110 m 全缆长范围内拖缆深度变化为 0.4 m；在 4 kn 航速下，拖缆的深度变化也仅有 1.7 m，因此可以将其看作处于零浮力状态。由表 2 和图 3 可知，随着航速的提高，线列阵在拖点处拉力不断增大，即其受到的阻力不断增大；整体线列阵拖缆的深度变化逐渐变小，每一小段的深度波动也变小，即整根线列阵拖缆变得越来越平直。

2 线列阵阻力特性试验研究 2.1 试验对象

本次试验按照实际的线列阵方案，参考仿真时的线列阵参数，加工了实尺度模型，确保仿真与试验满足相似准则。试验模型如图 4 所示。

2.2 试验方法

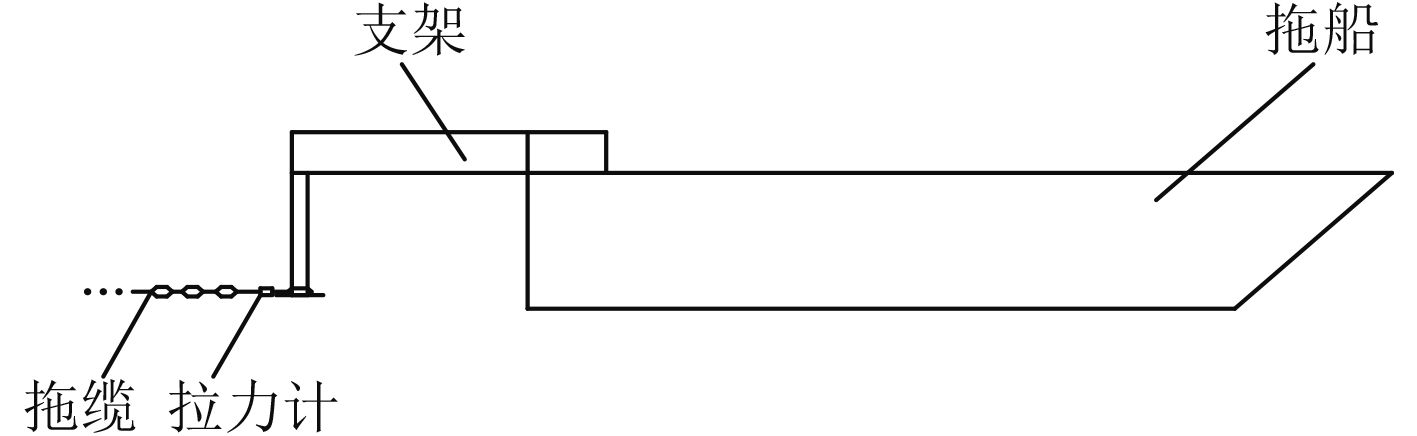
本试验中线列阵拖缆长度长，航速高，室内试验水池不具备试验条件，因此选择在湖中开展试验。针对研究的线列阵制作了 1:1 实尺度试验模型，采用专用固定支架将线列阵固定在拖船上，固定支架安装在拖船尾部，支架末端点处伸入水中 1 m，作为线列阵拖点。此时满足线列阵水下深度大于其直径 3 倍的关系，故可以不考虑兴波阻力的影响。具体试验装置如图 5 所示。

试验中航行速度用船用多普勒计程仪测量，测量精度为 1%；线列阵拖缆拉力用分体式数显拉力计测量，测量精度为 0.5%，均满足精度要求。

试验主要测量线列阵拖缆在水平直航时不同工况下的阻力，具体试验方案如下：

测试拖曳线列阵在航速 4，6，8，10 kn 直航状态下的阻力。拖船航行至试验区域后，先缓慢航行并抛缆，之后沿直线依次跑至 4，6，8，10 kn，待各航速稳定后，多次读取测力计数显屏显示数据并记录，以减少测量误差的影响。

2.3 试验结果分析

选线列阵拖缆在水中自由伸长状态为测力计重新置 0，记录不同航速下线列阵拖缆的阻力。

水平直拖试验中，拖船稳定航速 4，6，8，10 kn 时记录线列阵拖缆的阻力值，阻力测量值如表 3 所示，每个航速下分别采集了 3 个数据，取平均值，以减小单次数据采集带来的误差。水平直拖试验线列阵拖缆位形如图 6 所示。

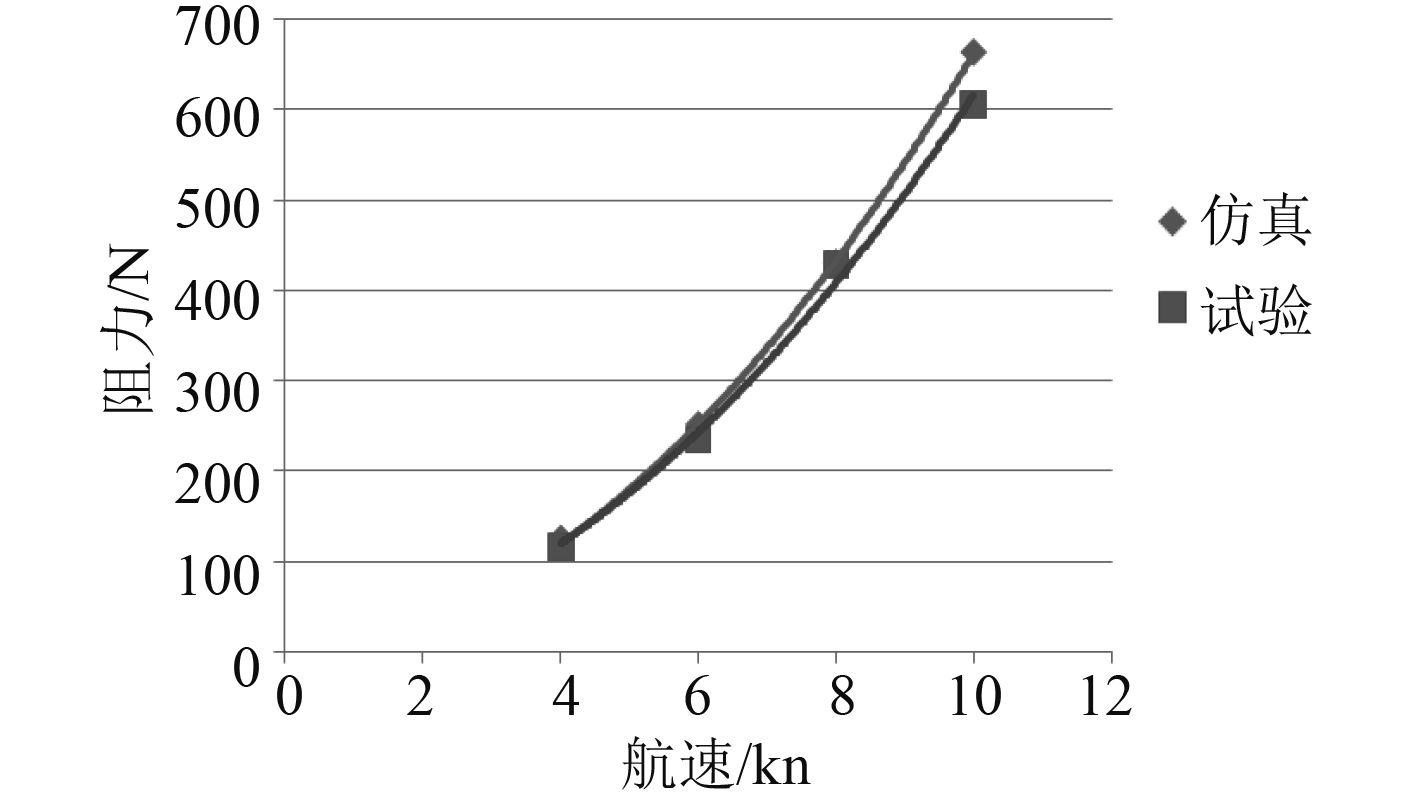
　　将仿真结果表 2 与试验所得数据表 3 进行比较，如图 7 所示，可以看出两者相差不大，最大误差在 10% 以内，且变化趋势一致，验证了数学仿真手段的可靠性。从图中可以看到，低航速时两者基本重合，在高航速时仿真值略大。分析其原因是由于建立线列阵拖缆模型时进行了简化所致。线列阵拖缆的阻力系数与航速及其和水平面的夹角有关。航速越高，阻力系数越小；夹角越大，其阻力系数则越大。但在一定范围内总体变化不大。仿真时因为线列阵拖缆为零浮力，在水中其姿态近乎水平，所以为了简化模型，采用固定阻力系数进行仿真，从而导致仿真值比试验结果偏大。

3 结　语

本文建立了一种水下非均质拖曳线列阵动力学仿真的方法，利用该方法对线列阵拖缆进行仿真分析，并设计开展试验对其结果进行验证，得到如下结论：

1）通过仿真分析结果，发现随着航速的提高，线列阵在拖点处拉力不断增大，即其受到的阻力不断增大；整体线列阵拖缆的深度变化逐渐变小，每一小段的深度波动也变小，即整根线列阵拖缆变得越来越平直。

2）仿真结果与试验数据对比分析可知，两者相差不大，最大误差在 10% 以内，且变化趋势一致，验证了本文针对分均质拖曳线列阵提出的仿真方法有效可靠。在高航速时仿真值略大，其原因是由于仿真时对模型进行了简化处理。

本文提出的仿真方法为进一步开展非均质拖曳线列阵的动力学分析，以及评估其对拖曳载体航行的影响奠定了基础。