2. 北京理工大学,北京 100081
2. Beijing Institute of Technology, Beijing 100081, China
不依靠自身动力系统,通过外加动力将运载器进行发射的方式称为弹射,也叫冷发射[1]。采用弹射技术后,运载器在自身动力启动前就已经获得了一定的初速度,故在装药量相同的条件下,增加了运载器的航程;或在不改变水下运载器航程的情况下,提高运载能力[2]。目前的弹射方式主要有炮式、液压式、压缩空气式、液压-气动式、燃气式、燃气-蒸汽式和电磁式等[3]。在诸多的弹射方式中,燃气-蒸汽式弹射以其结构简单可靠而备受青睐,运载体离筒过程中,筒内温度适中、压强及加速度变化平稳、加速快、能量输出可调,各内弹道参数均比较理想,应用广泛。
燃气-蒸汽式弹射的工作过程为:点火后,从燃气发生器喷管喷出的高温高速燃气流与冷却器内的冷却介质(通常为液态水)进行充分的热交换,形成混合蒸汽,使燃气温度降到允许的温度,后进入初容室,推动运载器运动[2]。在运载器运动过程中,筒内的流场变化极其复杂,除燃气自身的流动外,燃气还将使冷却水剧烈汽化产生水蒸气,并通过压差将冷却水和水蒸气推入初容室内。因此,燃气-蒸汽弹射的发射过程是一个包含复杂的传热、传质现象的多相流过程。
燃气发生器产生的燃气温度通常在 2 000 K 以上,如果弹射装置设计不当,则可能导致冷却水汽化不完全,高温气体将对运载器或装置造成冲击烧蚀,导致装置故障或引发事故。因此,有必要对弹射装置内流场进行深入研究,为弹射装置的设计和改进提供理论指导。
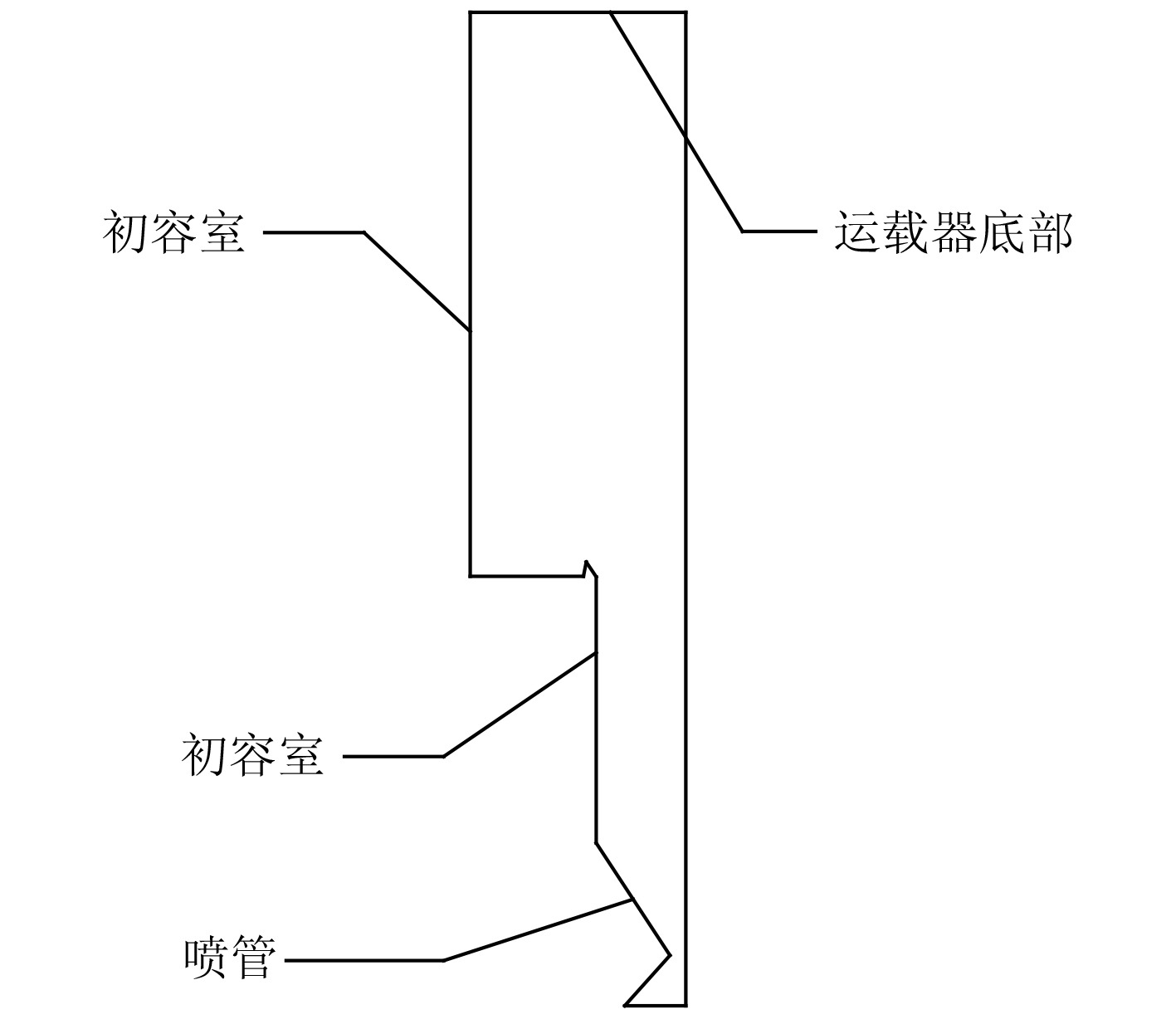
1 数学建模 1.1 物理模型燃气-蒸汽式弹射装置的物理模型如图 1 所示,由喷管、水室、初容室、运载器(底部)所组成。图示位置为初始位置,由于物理模型的轴对称性,本文采用二维轴对称建模,右边界为轴对称边界,下边界为压力入口边界,其余边界为壁面边界,采用无滑移绝热壁面边界条件,近壁面湍流计算采用标准壁面函数模型。此外运载器底部为运动边界,结合动网格技术实现计算域的变形,整个计算域为运载器底部向上运动至筒口。
|
图 1 物理模型 Fig. 1 Physical model |
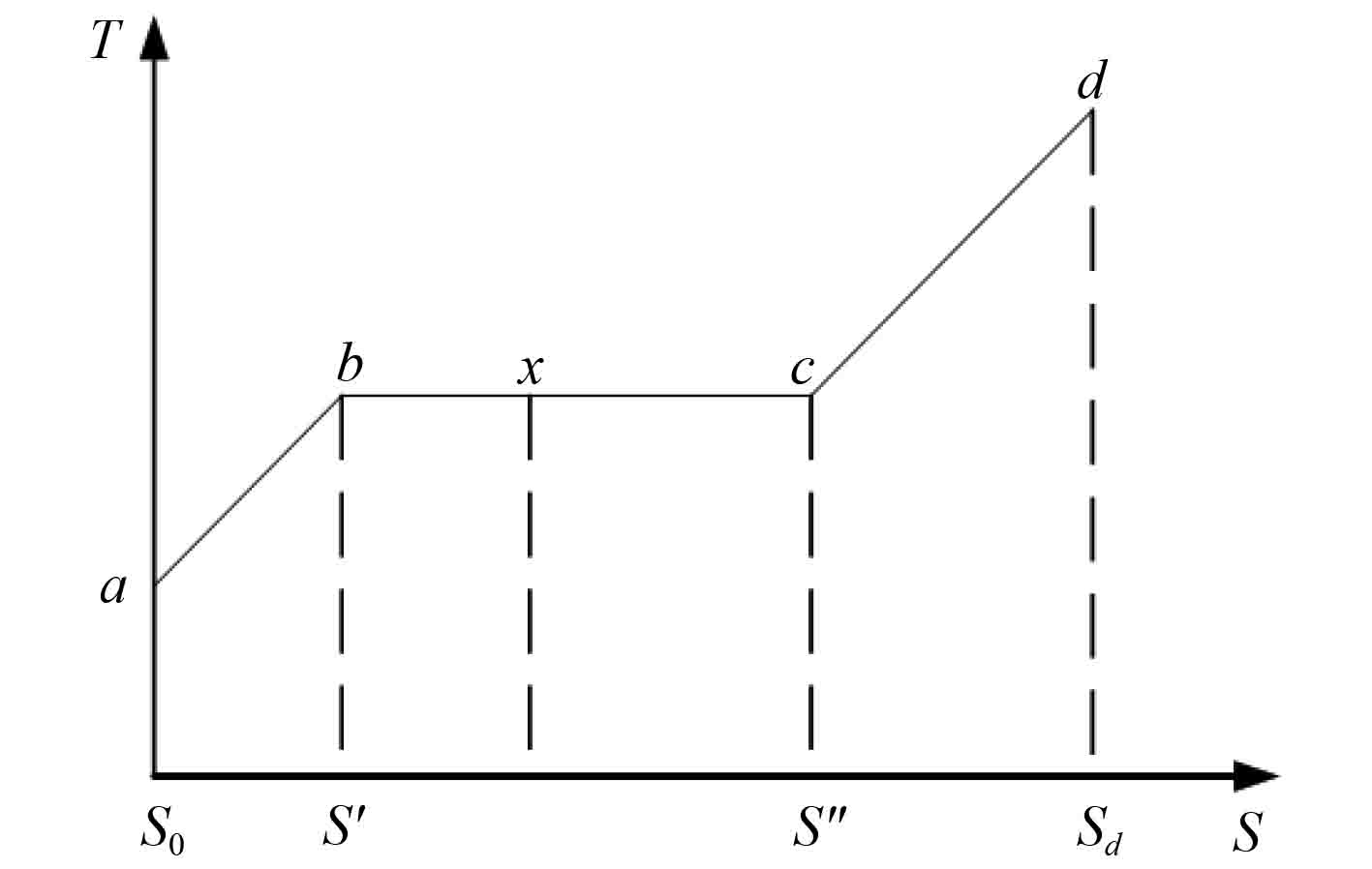
假设有 1 kg 水,其初始温度为tl ,比容为vl 。对水加热,使之变为过热蒸汽,则全部过程可分为 3 个阶段[4],如下面的温-熵图所示(图 2 中b 点参数用“'”表示,c 点参数用“"”表示)。
|
图 2 水汽化过程示意图 Fig. 2 Diagram of water vaporization process |
1)定压加热阶段
这一阶段如图中a–b 所示,其目的是将处于状态a 的未饱和水加热至饱和状态b,在这一过程中,温度由初温升至b 点的沸腾温度ts ,比容略有增加,所需的热量为:
| ${q_l} = h' - {h_l} = \left( {u' - {u_l}} \right) + p\left( {v' - {v_l}} \right)\text{,}$ | (1) |
在此过程中比容变化可忽略不计,故
| ${q_l} = u' - {u_l}\text{。}$ | (2) |
2)水的定压汽化阶段
对b 点饱和水继续加热,水开始沸腾汽化。汽化过程中,水蒸气与水的温度、压力均保持不变,但饱和水和饱和蒸汽二者所组成的混合物(称为湿蒸汽)的比容迅速增加。当水完全变为水蒸气时,汽化过程结束。此时蒸汽不再含有饱和水,称此时的蒸汽为干饱和蒸汽。由饱和水b 变为干饱和蒸汽c 的过程由图中的b–c 线所示。显然b–c 线既是等压线又是等温线,但含饱和蒸汽的质量不同。为了确定湿蒸汽的状态,除了要知道饱和温度ts (或饱和压力ps )外,还需知道另一个参数——干度x,即在饱和状态下,饱和汽占饱和水和饱和汽总和的百分数。
定压汽化过程中所需的热叫做汽化潜热,若干蒸汽状态用“"”表示,则过程中的能量转换过程的汽化潜热应为:
| $\Delta H = h'' - h' = \left( {u'' - u'} \right) + p\left( {v'' - v'} \right)\text{。}$ | (3) |
3)定压过热阶段
对于干饱和蒸汽c 继续加热,则干蒸汽的温度升高。将温度高于该压力下饱和温度的蒸汽称为过热蒸汽。过热蒸汽的温度与同压下的饱和温度之差称为过热度。定压过热过程由图中的c–d 线表示,该阶段所需之热量用q 表示,则有:
| $q = h - h'' = \int_{{t_s}}^t {{C_p}{\rm d}t} = {C_p}(t - {t_s})\text{,}$ | (4) |
式中Cp 为平均定压比热。
综合考虑上述 3 式,则若有 1 kg 水变成温度为t 的过热水蒸气,在此过程中所吸收的热量为:
| $Q = {q_l} + \Delta H + q = {C_l}({t_s} - {t_l}) + \Delta H + {C_p}(t - {t_s})\text{。}$ | (5) |
发射过程中,高温高压的燃气冲破水膜,并从喷管进入水室,由于燃气的温度很高,在燃气和冷却水的交界面上会产生剧烈的汽化效应。计算时对计算区域中的每一个网格内的气相和液相流体进行求解,当液态水的温度高于饱和温度时,液态水吸收热量汽化为水蒸气;当水蒸气的温度低于或等于饱和温度时,水蒸气凝结为液态水。计算中根据水的饱和温度计算水的汽化率,得到的计算模型表示如下:
液态水汽化公式为
| ${\dot m_l} = \left\{ \begin{aligned}& {\lambda _l}{\alpha _l}{\rho _l}\left| {{T_l} - {T_{sat}}} \right|/{T_{sat}}, {T_l} \geqslant {T_{sat}}\text{,}\\& 0, {T_l} < {T_{sat}}\text{;}\end{aligned} \right.$ | (6) |
水蒸汽凝结公式为
| ${\dot m_v} = \left\{ \begin{aligned}0, {T_v} \geqslant {T_{sat}}\text{,} \quad \quad \quad \quad \quad \quad \quad \quad \\{\lambda _v}{\alpha _v}{\rho _v}\left| {{T_v} - {T_{sat}}} \right|/{T_{sat}}, {T_v} < {T_{sat}}\text{。}\end{aligned} \right.$ | (7) |
式中:
某一网格内液态水的净汽化率为:
| $\dot m = {\dot m_l} - {\dot m_v}\text{,}$ | (8) |
水汽化造成的能量变化为:
| ${S_k} = - \Delta H\dot m \text{。}$ | (9) |
式中:sh
为水汽化吸收的能量或水蒸汽凝结释放的能量;当
在弹射过程中,流场中除燃气外,还存在液态水汽化而来的水蒸汽以及初始时刻的少量空气。当压力小于 20 MPa、温度大于 1 400 K 时,可将燃气和空气作理想气体处理,但由于汽化而来的水蒸汽离液态不远,将其简化为理想气体具有一定偏差,在此有必要将水蒸汽作真实气体考虑,并对其应用真实气体状态方程。
对水蒸汽应用Soave-Redlich-Kwong真实气体模型[5 –7]:
| $P = \frac{{RT}}{{V - b}} - \frac{{a(T)}}{{{V^2} + bV}}\text{,}$ | (10) |
其中:
| $\left\{ \begin{aligned}& a(T) = {a_0}{\{ 1 + n[1 - {(T/{T_c})^{0.5}}]\} ^2}\text{,}\\& n = 0.48 + 1.574\omega - 0.17{\omega ^2}\text{。}\end{aligned} \right.$ | (11) |
组分输运模型中第i 组分的守恒方程为:
| $\frac{\partial }{{\partial t}}\left( {\rho {Y_i}} \right) + \nabla \cdot \left( {\rho \overrightarrow \upsilon {Y_i}} \right) = - \nabla \cdot \overrightarrow {{J_i}} + {S_i}\text{,}$ | (12) |
式中Yi 为组分i 的质量分数。若总的组分数为N,则
| $\sum\limits_{i = 1}^N {{Y_i}} = 1\text{。}$ | (13) |
通过求解前N–1 种组分的守恒方程,则第N 种组分的质量分数可由上式得出。
将组分输运守恒方程应用于多相流模型中时,对q 相的第i 种组分,其守恒方程变为:
| $\begin{aligned}\frac{\partial }{{\partial t}} & \left( {{\rho ^q}{\alpha ^q}{Y_i}^q} \right) + \nabla \cdot \left( {{\rho ^q}{\alpha ^q}{{\vec \upsilon }^q}{Y_i}^q} \right) = \\& - \nabla \cdot {\alpha ^q}{\overrightarrow {{J_i}} ^q} + {\alpha ^q}{S_i} + \sum\limits_{p = 1}^n {\left( {{{\dot m}_{{p^i}{q^j}}} - {{\dot m}_{{q^j}{p^i}}}} \right)} \text{。}\end{aligned} $ | (14) |
式中:
本文采用 3 种仿真模型对燃气-蒸汽式弹射内弹道进行了计算分析, 3 种计算工况如表 1 所示。工况 1 不考虑汽化效应,即假设冷却水不发生汽化,仅靠吸热提高自身温度给流场降温,因此工况 1 中气相可作为一种理想气体[8]处理,其物性参数取燃气的平均参数,由表 2 中的各组分加权平均得到;工况 2 在工况 1 的基础上加入汽化模型,但气相的处理方式不变,即工况 2 中液相的冷却水经汽化转化为气相混合气体,混合气体的物性参数取燃气的平均参数;工况 3 在工况 2 的基础上引入组分输运模型,将气相作为燃气、空气和水蒸气 3 种组分的混合气体,液相的冷却水经汽化转化为气相中的水蒸气组分。
|
|
表 1 计算工况说明 Tab.1 Calculation conditions |
|
|
表 2 燃气组分表 Tab.2 Gas component |
仿真起始时刻由喷管破膜时刻开始,筒中的预充压力为 1 个大气压,即 101 325 Pa,温度 300 K;图 3 为初始时刻流场中气液两相的分布图,冷却水集中放置于水室。气体为发射筒的预充气体,工况 1 和工况 2 中该气体为应用燃气物性参数的理想混合气体;工况 3 中该气体为空气,且初始时刻流场中不含燃气和水蒸气,仿真开始后燃气由喷管入口进入流场,水蒸气为由发射过程中的冷却水汽化得到。

|
图 3 初始时刻气液两相分布图 Fig. 3 Gas-liquid two-phase distribution at the initial time |
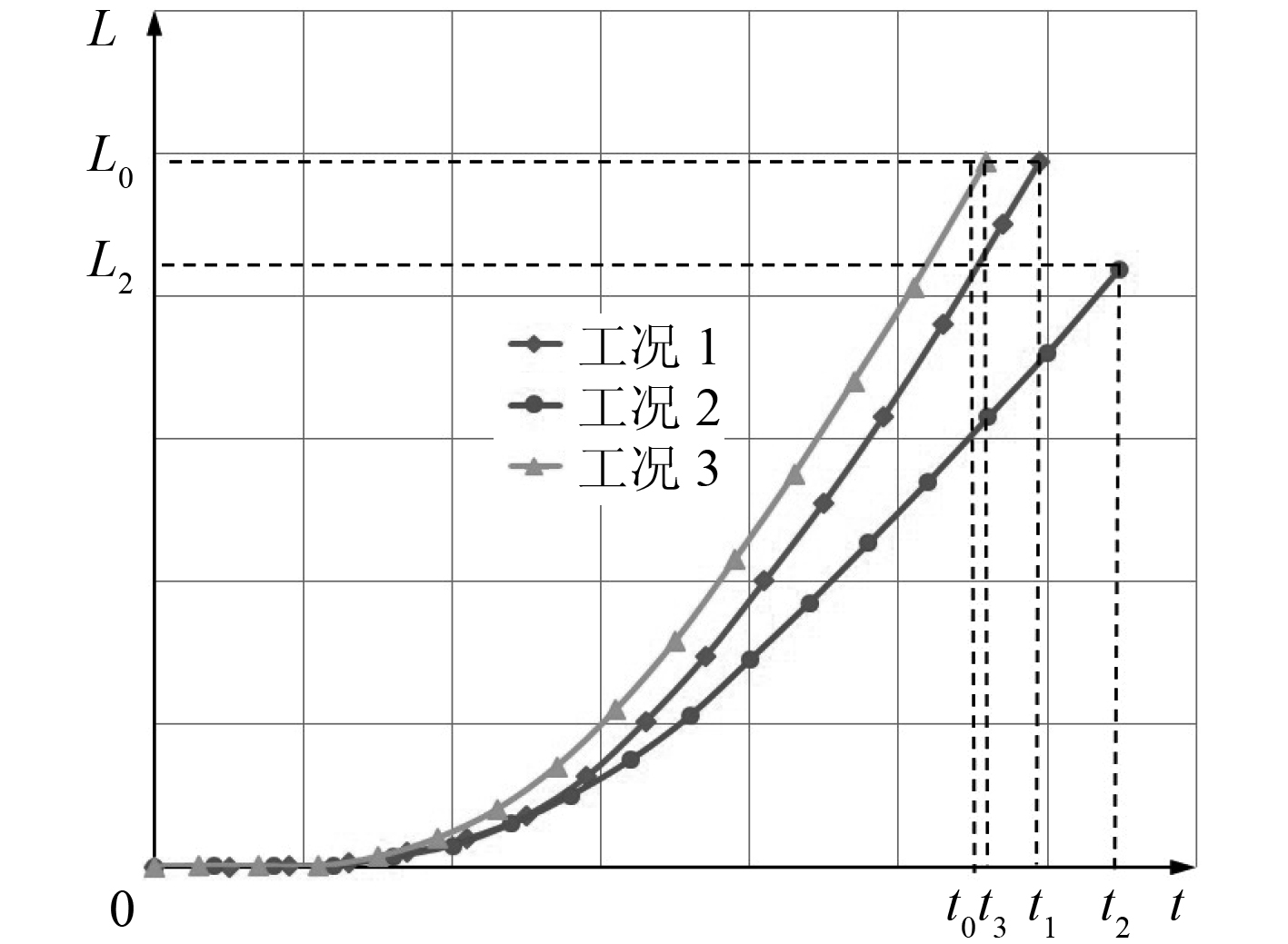
运载器出筒距离为L0,即当运动壁面(运载器底部)向筒口方向运动L0 后仿真结束。本文通过对 3 种工况下的内弹道过程进行比较,从而对 3 种仿真模型进行分析对比。图 4 为运载器位移曲线,工况 1 与工况 3 中运载器分别于t1,t3 时刻离筒,而工况 2 在燃烧室的推进剂燃烧结束时刻(t2)位移仅为L2(L2 <L0),表明运载器在t2 时刻并未离筒。该弹射装置的设计工作t0 与t1,t3 较为接近,说明工况 1 与工况 3 的计算模型与实际较为相符,而工况 2 的仿真结果误差较大,说明在仿真计算时仅引入汽化模型,而不同时使用组分输运模型,将会造成仿真结果误差较大。
|
图 4 运载器位移曲线 Fig. 4 The displacement curve of vehicle |
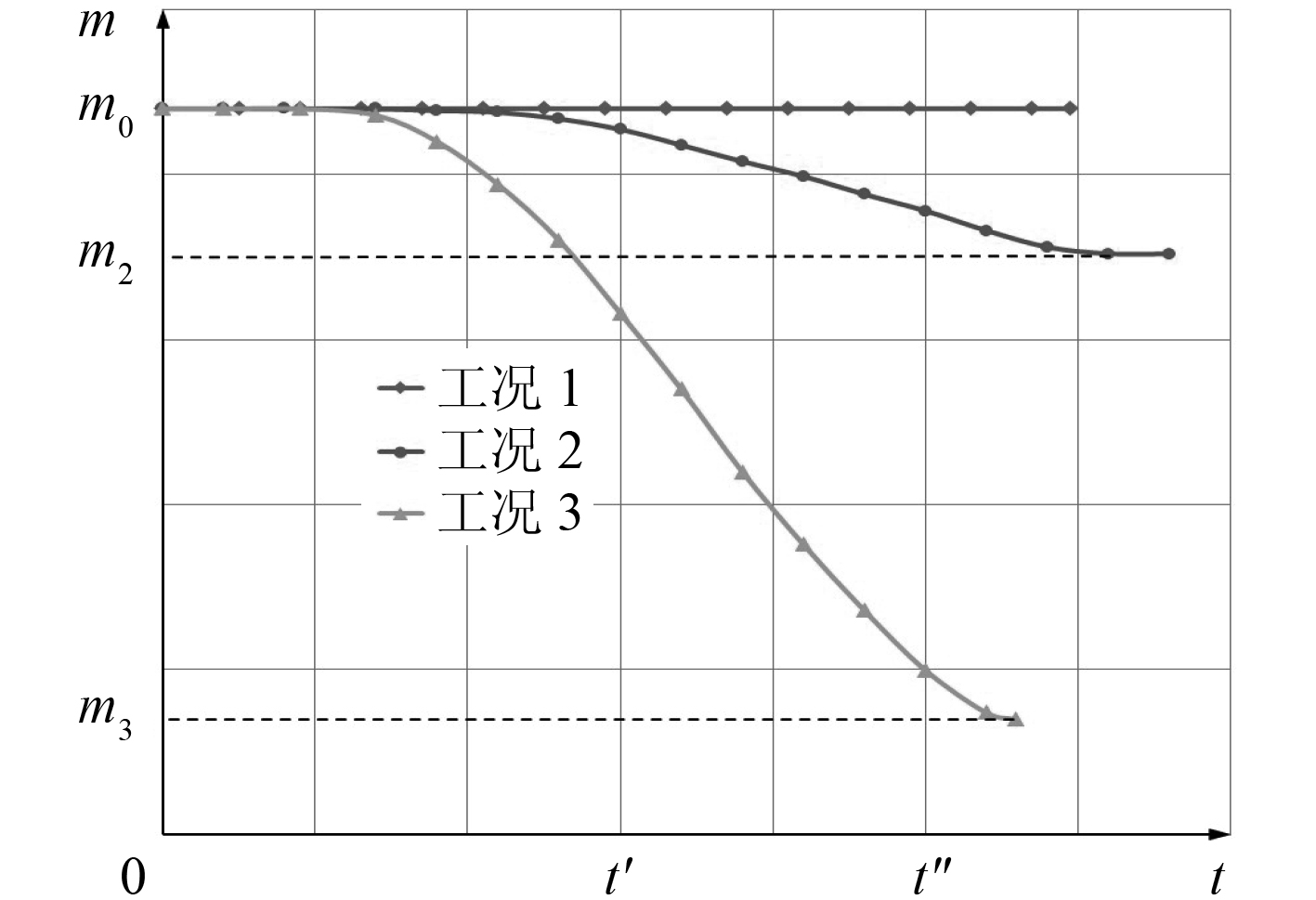
图 5 为 3 种工况下液态冷却水的质量变化曲线。由图可知,工况 1 未加入汽化模型,所以仿真过程中的液态冷却水质量不变。工况 2 的液态水汽化速度较慢,汽化率约 20%。工况 3 汽化率达到了 88%,汽化效果较好。
|
图 5 液态冷却水质量变化曲线 Fig. 5 The mass curve of liquid water |
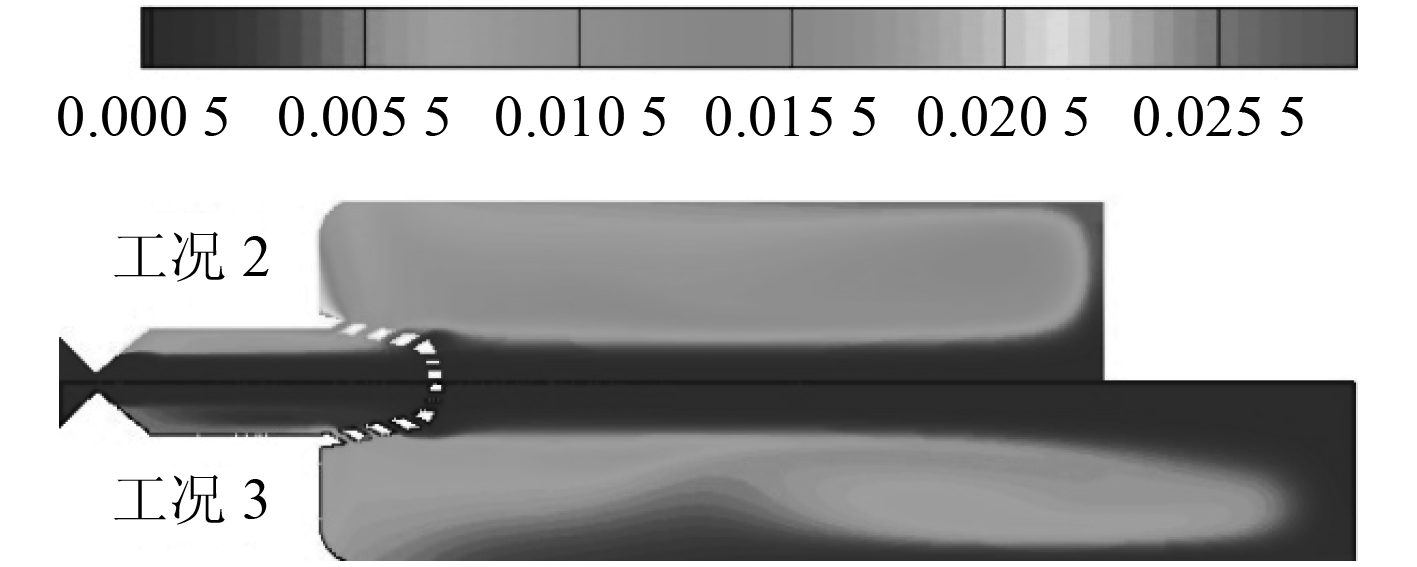
工况 2 中的汽化速度和汽化率明显小于工况 3,由汽化模型中水的汽化速率方程可知,发生液态水的汽化现象时,网格内液态水的体积分数越高、温度越高,则汽化速率越快。工况 2 和工况 3 在t'时刻的冷却水体积分数分布图和温度分布图如图 6和图7 所示。从图中可看出,两者的冷却水体积分数相当,而工况 3 的高温区明显比工况 2 范围大,因此工况 3 的汽化速率更大。
|
图 6 t’时刻工况 2 与工况 3 冷却水体积分数云图 Fig. 6 Volume fraction of cooling water in condition 2 and condition 3 att' moment |

|
图 7 t' 时刻工况 2 与工况 3 流场温度云图 Fig. 7 Temperature contour in condition 2 and 3 att' moment |
工况 3 在t"时刻的燃气和水蒸气的体积分数分布图如图 8和图9 所示。从图中可看出,水蒸气主要分布于冷却水以及冷却水与燃气交界面处,即汽化产生的水蒸气充当了燃气和冷却水的传热媒介,而水蒸气的导热系数较燃气高,因此工况 3 中冷却水获得的能量更多,汽化速率更大。

|
图 8 t" 时刻工况 3 燃气体积分数云图 Fig. 8 Volume fraction of gas in condition 3 att" moment |

|
图 9 t" 时刻工况 3 水蒸气体积分数云图 Fig. 9 Volume fraction of steam in condition 3 att" moment |
工况 2 与工况 3 的区别在于工况 3 使用了组分输运模型,计算中考虑水蒸气与燃气、空气性质的差异,将水蒸气单独作为气相的一种组分,仿真结果证明工况 3 的计算模型与实际更为相符。
表 3 为 3 种工况下部分参数的仿真结果。对比工况 1 和工况 3,考虑汽化效应后,运载器底部的最大平均压力升高了 14.3%,最大平均温度降低了 16.5%,筒内最大平均温度则降低了 52.2%,而离筒速度则仅仅提高了 4.4%,离筒时间降低了 6.1%,这说明增加汽化效应后的仿真流场对压力有一定影响,但相对较小,所以能够得到比较相近的位移曲线,但对温度的影响很大,而温度是燃气-蒸汽式弹射装置的一个重要指标,所以在进行仿真时必须要考虑汽化效应。工况 2 中运载未能离筒,且压力、温度、冷却水汽化率都与工况 1、工况 3 偏差均较大,仿真结果误差较大,说明使用汽化模型时,必须结合使用组分输运模型,考虑水蒸气与燃气、空气性质的差异,将水蒸气单独作为气相的一种组分进行处理,否则造成的仿真结果失真。
|
|
表 3 仿真结果对比 Tab.3 Comparison of simulation results |
本文对燃气-蒸汽式弹射内弹道采用 3 种仿真模型进行计算,并以工况 3 的仿真结果为基础,深入研究了弹射过程中气液两相流的变化过程,仿真结果表明:
1)对燃气-蒸汽式弹射装置进行流场仿真计算时应考虑汽化效应的影响,汽化效应对流场的温度较压力、速度的影响更明显。
2)由于水蒸气与燃气、空气的物理性质差异较大,在两相流模型中耦合汽化模型时,需同时引入组分输运模型,否则仿真结果误差较大。
| [1] | 袁曾凤.火箭导弹弹射内弹道学[M].北京:北京工业学院出版社, 1987. |
| [2] | 刘永泉, 郗安民, 刘鸿飞. 导弹燃气-蒸汽弹射发射技术概述[J].飞航导弹, 2009(12): 23–25, 29. |
| [3] |
芮守祯, 邢玉明. 导弹发射动力系统发展研究[J]. 战术导弹技术, 2009(5): 4–9, 61.
RUI Shou-zhen, XING Yu-ming. Development research on missile launching power system[J] Tactical Missile Technology, 2009(5): 4–9, 61. |
| [4] | 赵险峰, 王俊杰. 潜地弹道导弹发射系统内弹道学[M]. 哈尔滨: 哈尔滨工程大学出版社, 2001. |
| [5] | 佘守贤.真实气体与气液相变[M].北京:人民教育出版社, 1963. |
| [6] | MANNINEN M, TAIVASSALO V, KALLIO S. On the mixture model for multiphase flow[R]. VTT Publications 288, Technical Research Centre of Finland, 1996. |
| [7] | 鲍廷钰, 邱文坚.内弹道学[M].北京:北京理工大学出版社, 1995. |
| [8] | 王保国, 刘淑艳, 黄伟光. 气体动力学[M]. 北京: 北京理工大学出版社, 2005. |
 2017, Vol. 39
2017, Vol. 39
