海洋资源和海洋空间的开发利用在我国的可持续发展中显得越来越重要,近年来,水下运载器在海洋环境研究、资源勘探等方面显示出巨大的应用价值[1]。水下滑翔机是一种不依靠外部推进装置的水下自主航行器,它通过浮力调节机构改变自身的净浮力和姿态调节机构调整内部重心位置,从而实现了滑翔机在垂直面的锯齿运动和螺旋下潜运动[2]。因此,优良的水动力性能对水下滑翔机操纵与运动至关重要。
水下滑翔机由机体、机翼及附体 3 个部分组成[3]。随着国家对海洋领域投入大量资金与精力,国内学者对滑翔机的外形设计与水动力性能进行了一系列的研究,但主要以 Spray[4],Slocum[5]和 Seaglider[6]三种典型滑翔机为设计参考,在此基础上进行优化与改进,以满足工程应用,并获得更佳的水动力性能。
水下滑翔机大多数时间是在深水中工作,因此大多数情况下不考虑自由液面、波浪对其运动的影响。水下滑翔机在水中运动时,所受到的水动力可以分为粘性水动力和惯性水动力两类,其中对水下滑翔机粘性水动力系数的计算与分析是本文的重点。粘性水动力系数主要有 4 种来源[7],分别是根据母型估算;约束模型试验;CFD 数值计算;实航数据的系统辨识。其中由于水下滑翔机种类较多,设计各异,目前没有较为统一的近似计算公式和资料;约束模型试验结果较精确,但试验时间长,成本高;CFD 数值计算适用范围广,成本低,操作简单;系统辨识是对约束模型试验的再验证,不适合在水下滑翔机设计之初进行分析与指导,且国内相关研究相对较少。
目前国内外对水下滑翔机的水动力求解多采用 CFD 数值计算的方法,其成本较低,适用性广,但由于未进行约束模型试验,其精度无法判断,对水下滑翔机的运动控制造成一定的不利影响。本文介绍了实验室所研制的水下滑翔机(“海鸥一号”)外形设计及优化,利用 CFD 软件对该滑翔机的粘性水动力进行计算与分析,并与约束模型试验的结果进行对比,验证了数值模拟的可行性与准确性,且在千岛湖湖泊试验中,相继实现了多组水下滑翔机锯齿运动和螺旋下潜运动,进一步证明结果满足工程精度需求,同时总结了该滑翔机水动力性能的特征,对今后水下滑翔机的设计与计算提供了帮助与指导。
1 水下滑翔机外形设计水下滑翔机在运动过程中,主要受到阻力和升力的作用,其中阻力主要由于水的粘性作用,使得滑翔机表面产生的摩擦力,同时由于主体前后部分存在压差从而产生粘压阻力。此外附体也会增加阻力,因此良好的外形设计是减少阻力的重要要求;升力[8]主要由滑翔机机翼的上下表面的压力差所产生,是滑翔机向前滑翔的动力,因此机翼的水动力性能直接影响到滑翔机的运动性能。
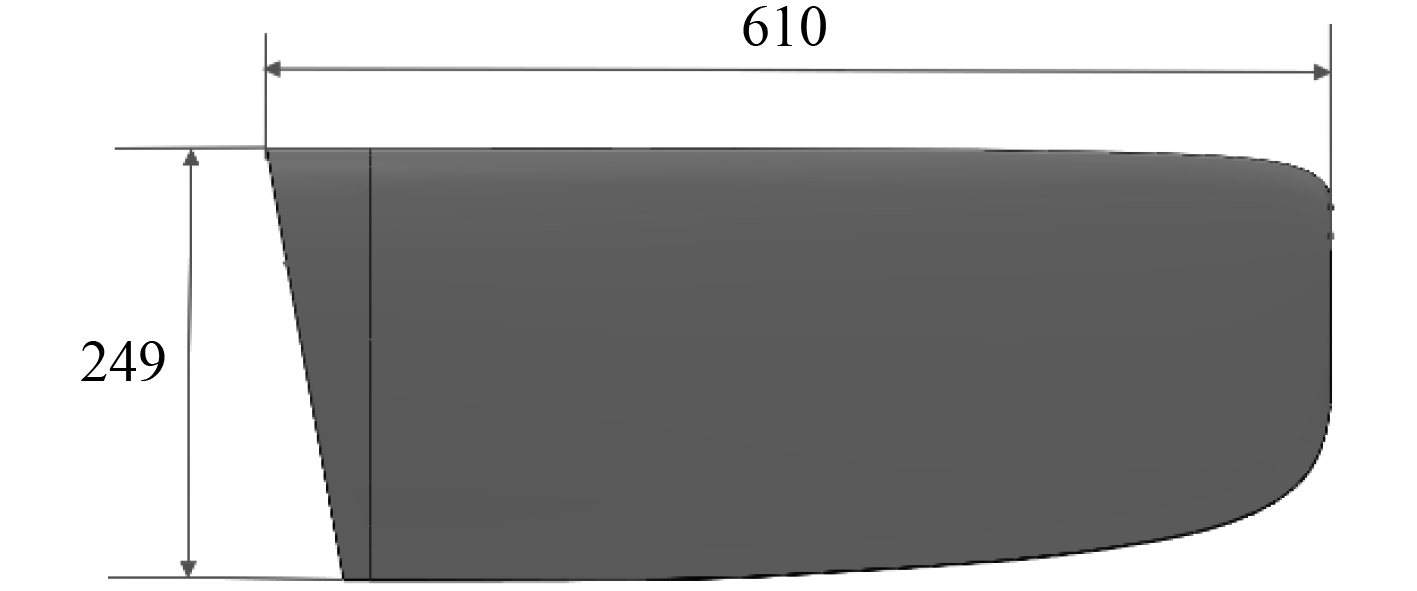
1.1 阻力阻力主要由摩擦力、粘压阻力和附体阻力构成,因此尽可能小的湿表面积和附体数量以及流线型设计均有利于减少阻力。海鸥一号采用流线型回转体,其外形如图 1 所示。与其他水下滑翔机相比,海鸥一号将 GPRS 天线置于尾舵中,达到了减少附体数量的目的,同时对通信天线起到很好的防水保护效果。

|
图 1 “海鸥一号”设计外形 Fig. 1 The design hull of the Seagull-1 glider |
|
图 2 “海鸥一号”机翼外形 Fig. 2 The wing of the Seagull-1 glider |
回转体头部和尾部的外形曲线分别由式(1)和式(2)生成,其中D0 为滑翔机主体最大横剖面直径,Le 和Lr 分别为进流段和去流段的长度,ne 和nr 分别为椭圆指数和抛物线指数。其中ne 和nr 最优值分别决定Le 和Lr 的大小,经过 ISIGHT 软件的优化,最终Le 和Lr 的长度分别是 200 mm 和 400 mm。
| ${y_e} = \frac{{{D_0}}}{2} \times {\left( {1 - {{\left( {\frac{x}{{{L_e}}}} \right)}^{{n_e}}}} \right)^{\frac{1}{{{n_e}}}}} {n_e} = 1.7\text{,}$ | (1) |
| ${y_r} = \frac{{{D_0}}}{2} \times {\left( {1 - {{\left( {\frac{x}{{{L_r}}}} \right)}^{{n_r}}}} \right)^{\frac{1}{{{{\rm{n}}_r}}}}} {n_r} = 3\text{。}$ | (2) |
升力主要由机翼产生,水下滑翔机在上浮、下潜过程中应该保持同样的滑翔姿态,因此多选取对称翼型。现有水下滑翔机机翼大多采用平板型机翼,其结构简单、加工方便、成本低,但其产生的升力小、水动力性能不佳,因而“海鸥一号”采用 NACA0012 翼型,以期提升运动性能。图 2 是“海鸥一号”的机翼外形,改变机翼固定的位置,经过多次 CFD 仿真计算,分析和对比在相同速度下阻力、升力、力矩的大小,最终选择将机翼固定于滑翔机重心位置。
1.3 水动力表达式水下滑翔机的水动力与滑翔机形状和运动状态密切相关,滑翔机在运动中受到的全部粘性水动力十分复杂,因此选择一种既能充分表现作用在滑翔机上的主要水动力又不过于复杂的表达式十分重要。
本文采取一种应用于对水下滑翔机运动仿真时的水动力表达式[9],即在速度坐标系中,水下滑翔机的水动力 F 和水动力矩T 可由下式表示:
| ${{F}} = \left[ {\begin{array}{*{20}{c}}{ - D}\\{SF}\\{ - L}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{({K_{D0}} + {K_D}{\alpha ^2}){{{v}}^2}}\\[6pt]{{K_\beta }\beta {{{v}}^2}}\\[6pt]{({K_{L0}} + {K_L}\alpha ){{{v}}^2}}\end{array}} \right]\text{,}$ | (3) |
| ${{T}} = \left[ {\begin{array}{*{20}{c}}{{T_1}}\\{{T_2}}\\{{T_3}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{({K_{MY}}\beta + {K_p}p){{{v}}^2}}\\[6pt]{({K_{M0}} + {K_M}\alpha + {K_q}q){{{v}}^2}}\\[6pt]{({K_{MZ}}\beta + {K_r}r){{{v}}^2}}\end{array}} \right]\text{。}$ | (4) |
式中:D,SF,L 分别为阻力、横向力和升力;T1,T2,T3 分别为横倾力矩、纵倾力矩和偏航力矩;α 和β 分别为滑翔机的攻角和漂角。

|
图 3 水下滑翔机坐标系 Fig. 3 Frame illustration of the underwater glider |
水下滑翔机工作时速度较小,因此在其运动过程中雷诺数较低。RNGk-ε 湍流模型是在标准k-ε 模型基础上进行改进,提高了在速度梯度较大的流场和强旋转流动时的计算精度,对低雷诺数的计算精度得到提升,因此在对斜航运动仿真时使用 RNGk-ε 湍流模型。对于旋转流动时,k-ω 湍流模型能精确地模拟定常回转运动,与标准k-ω 模型相比,SSTk-ω 模型结合了k-ε 和k-ω 两者优点,适用范围更广。2 个模型[10]的方程式为
| $\left\{ \begin{aligned} \frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial (\rho k{u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {{\alpha _k}{\mu _{eff}}\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} + \rho \varepsilon \text{,}\qquad (5)\\ \frac{{\partial (\rho \varepsilon )}}{{\partial t}} \!+\! \frac{{\partial (\rho \varepsilon {u_i})}}{{\partial {x_i}}} \!=\! \frac{\partial }{{\partial {x_j}}}\left[ {{\alpha _\varepsilon }{\mu _{eff}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] \!+\! \frac{{C_{1\varepsilon }^ * \varepsilon }}{k}{G_k} \!-\! {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k}\text{。}\end{aligned} \right.$ |
| $\left\{ \begin{aligned}& \frac{\partial }{{\partial t}}(\rho k) + \frac{\partial }{{\partial {x_i}}}(\rho k{u_i}) = \frac{\partial }{{\partial {x_j}}}({\Gamma _k}\frac{{\partial k}}{{\partial {x_j}}}) + {G_k} - {Y_k} + {S_k}\text{,}\\& \frac{\partial }{{\partial t}}(\rho \omega ) \!+\! \frac{\partial }{{\partial {x_i}}}(\rho \omega {u_i}) = \frac{\partial }{{\partial {x_j}}}({\Gamma _\omega }\frac{{\partial \omega }}{{\partial {x_j}}}) \!+\! {G_\omega } \!-\! {Y_\omega } \!+\! {S_\omega }\text{。}\end{aligned} \right.$ | (6) |
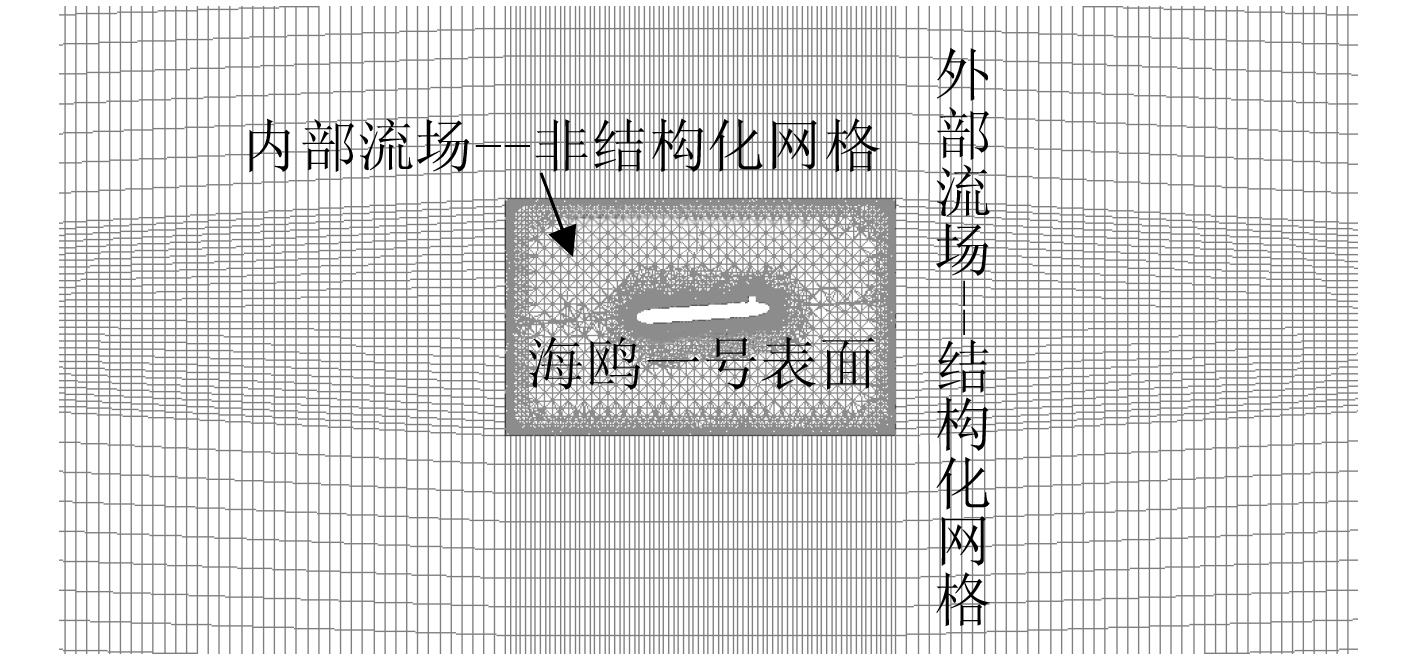
CFD 计算中,通常计算域越大,其计算精度越高,但计算域增大将会增加计算时间,对计算机要求也更加苛刻。因此,对水下滑翔机斜航运动进行仿真时,同时采用结构化网格和非结构化网格。其中计算域分成两部分,内部流场采用非结构化网格,因为非结构化网格贴体性强,适应复杂外形的求解,同时非结构化网格生成过程中不断进行优化判断,因而生成高质量网格;外部流场则采用结构化网格,从而减少网格数量,提高网格质量,加快运算时间。计算域范围为:– 6L≤x ≤ 6L,– 3L ≤y ≤ 3L,– 3L ≤z ≤ 3L。
对水下滑翔机定常回转运动进行仿真时,则全部采用非结构化网格。其计算域的选取需要根据水下滑翔机的主尺度和回转半径来确定。来流截面距离滑翔机前端约 2.5 倍体长,周围边界距离滑翔机中轴线约 1.5 倍体长,出流截面距离滑翔机后端约 2.5 倍体长。参考 FLUENT 手册对y+ 进行合理取值,y+ ≈ 20。2 种不同的运动仿真所使用的网格分别如图 4和图5 所示。
|
图 4 斜航运动网格划分 Fig. 4 The grid of the glider in linear motion |

|
图 5 定常回转运动网格划分 Fig. 5 The grid of the glider in turning motion |
对于斜航运动的仿真,外部流域入口边界条件设定为速度入口,外域流域出口边界条件为自由出流,海鸥一号表面设定为无滑移壁面条件,外域其他部分的边界条件为壁面条件,内外域通过 interface 连接,流体可自由穿过。
对于定常回转运动的仿真,入口的边界条件设置为速度入口(velocity inlet),利用用户自定义函数(UDF)功能对入流速度进行定义,通过使用 DEFINE_PROFILE 函数,使其满足角速度保持不变的条件
斜航运动和定常回转运动的控制方程均采用有限体积法进行离散,选择 SIMPLEC 方法处理压力与速度耦合问题,压力选项使用标准差分格式,动量、湍流动能和湍流耗散率均使用二阶迎风格式,使用 Gauss-Seidel迭代方法求解方程,利用 Ansys Fluent 完成计算。
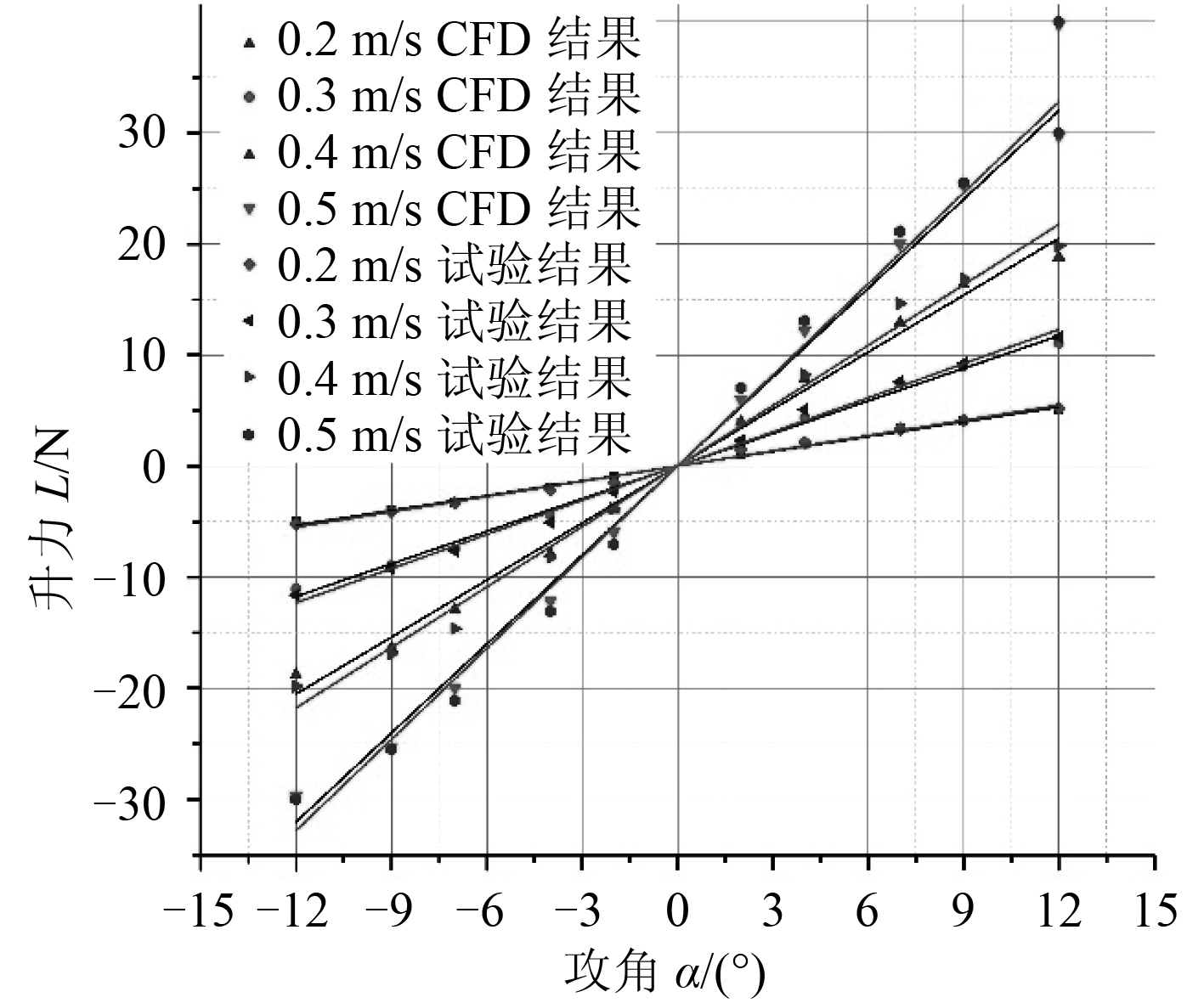
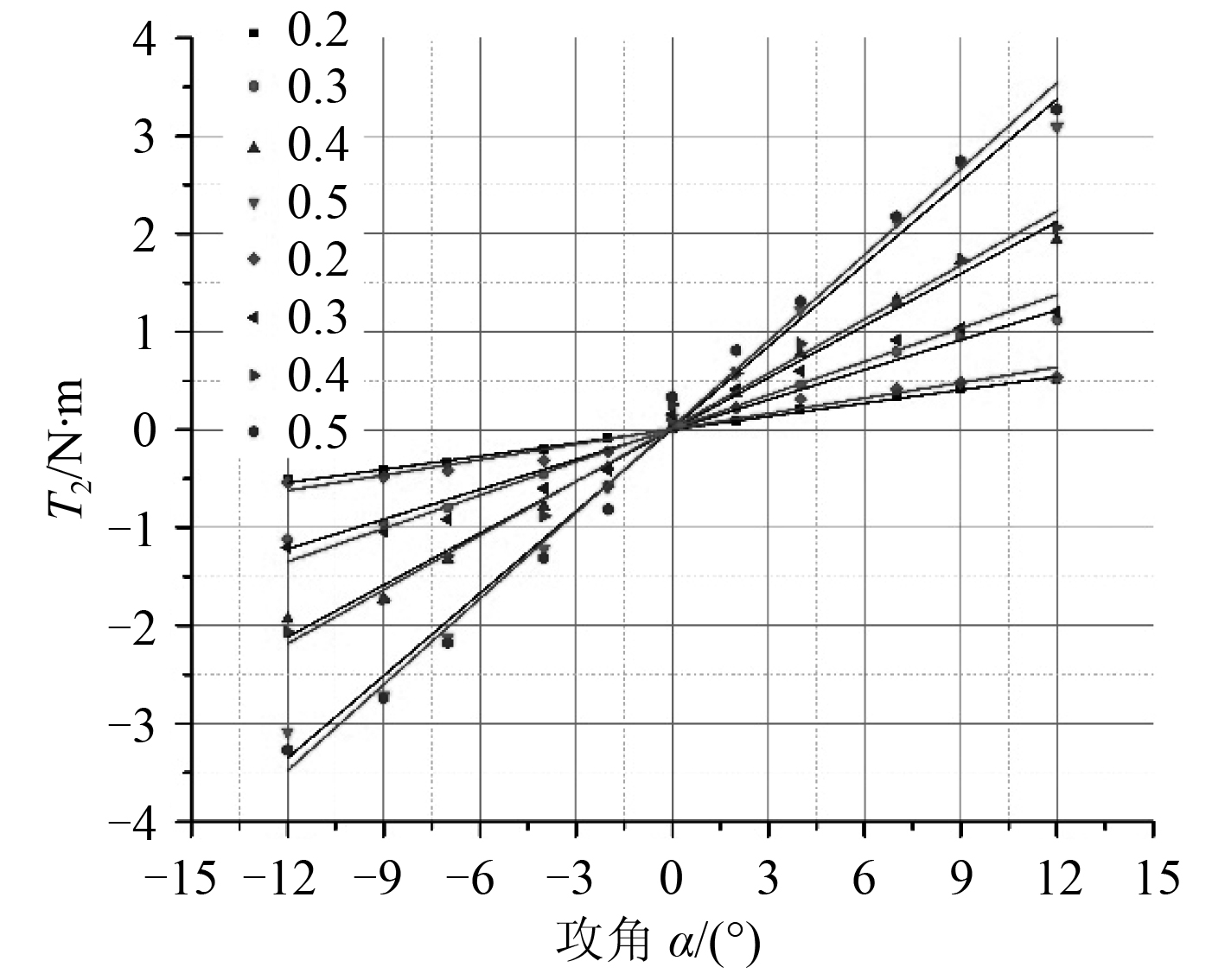
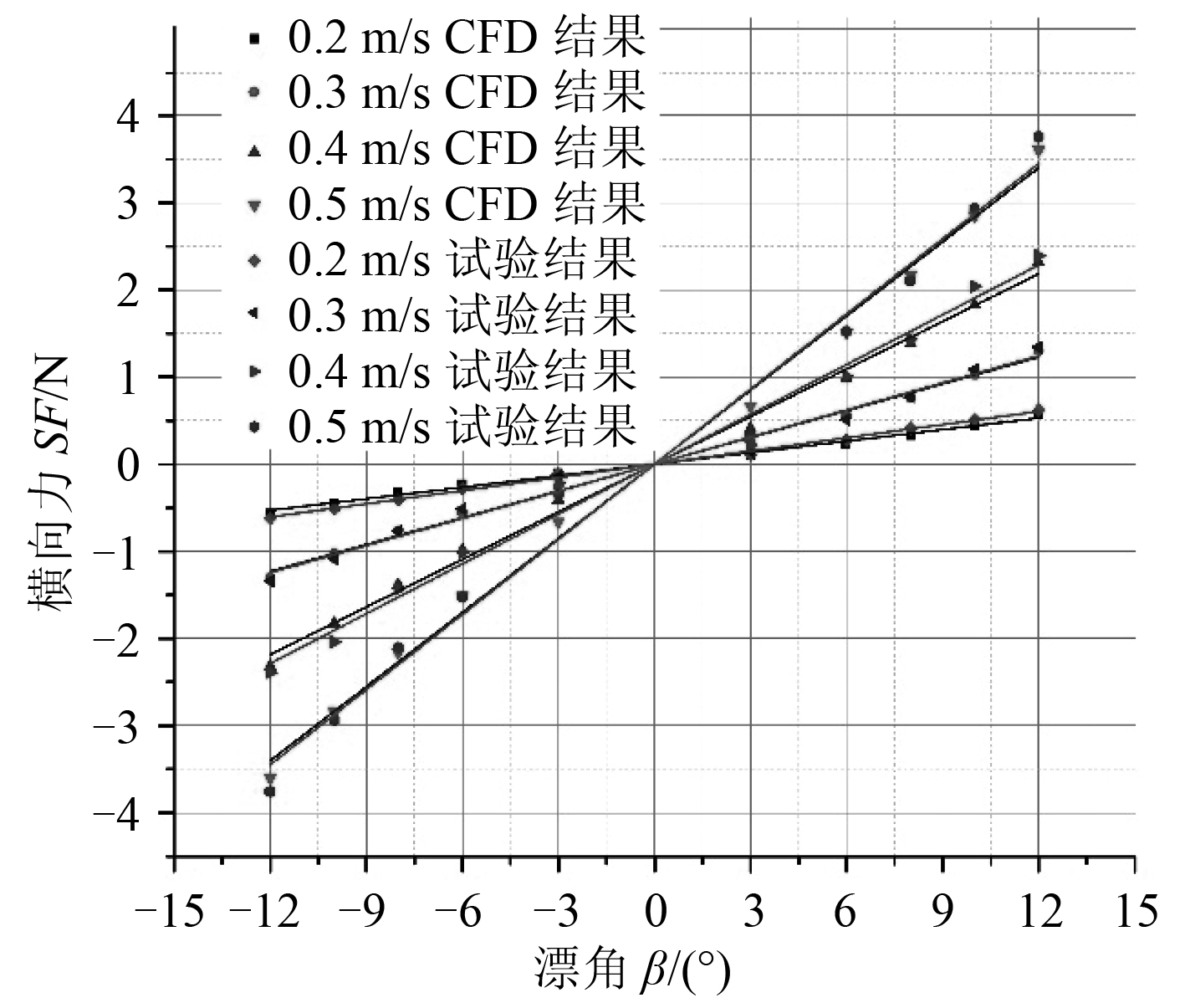
3 计算结果及分析 3.1 计算工况根据式(3)可知,阻力D 和升力L 只是攻角α 的函数,因此KD0,KD ,KL0,KL 可以通过斜航运动时不同攻角下的阻力和升力求解得到,如图 6 和图 7 所示。同理,在不同漂角下可以得到Kβ ,如图 9 所示。当q = 0 时,KM0 ,KM 可以通过斜航运动时改变攻角得到,如图 8 所示。

|
图 6 不同攻角下阻力变化 Fig. 6 The drag force with respect to α |
|
图 7 不同攻角下升力变化 Fig. 7 The lift force with respect toα |
|
图 8 不同攻角下纵倾力矩变化 Fig. 8 MomentT2 with respect toα |
|
图 9 不同漂角下横向力变化 Fig. 9 The side force with respect toβ |
根据式(4)可知,T3 是β 和r 的函数,因此通过分析在不同回转半径、不同漂角下滑翔机绕轴 π 3 转动时受到的偏航力矩,即可求得KMZ ,Kr 的值。同理,可求得KMY ,Kp ,Kq 的值。
3.2 拖曳试验拖曳试验使用了六维力扭矩传感器进行测试,在试验前期设计并加工出配套固定装置以便水下滑翔机的拖曳,各组拖曳工况与表 1 中k-ε 对应的仿真工况条件一致。试验结束后,将传感器所得到的数据导入 Origin 软件,利用低通滤波功能对数据进行处理,再求取稳定状态时力和力矩的平均值,进而确定不同攻角、不同漂角、不同速度下水下滑翔机所受到力和力矩的数值。
|
|
表 1 CFD 仿真计算工况 Tab.1 Combinations of parameter values for CFD simulation |
利用 CFD 软件对上述工况进行计算,所得到的部分力和力矩数值见图 6~图11,其中黑色线条为对 CFD 数值结果的拟合曲线。为了对斜航运动数值计算结果的精确度进行验证,在拖曳水池中同样进行了与表 1 中相同工况的拖曳试验,试验结果的拟合曲线为图中浅色线条。基于式(3)和式(4)使用 Origin 软件对结果进行拟合,即可求出水下滑翔机的各个水动力系数,其结果如表 2 所示。其中误差计算以试验结果为真实值,以 CFD 结果为测量值。

|
图 6 不同攻角下阻力变化 Fig. 6 The drag force with respect to α |

|
图 10 不同漂角下偏航力矩变化 Fig. 10 MomentT3 with respect toβ |

|
图 11 不同攻角下升阻比变化 Fig. 11 Ration of lift and drag force |
|
|
表 2 CFD 与试验所得的水动力系数 Tab.2 Hydrodynamic coefficients of the glider from CFD simulation and towing experiments |
由图 6~图7 可知,滑翔机的阻力和升力随着速度和攻角的增大而增大,但升力关于攻角成线性增长,而阻力关于攻角成平方次增长。由图 6~图11 可知,CFD 仿真结果和拖曳试验结果均与式(3)和式(4)的表达式一致,证明该方程式适合水下滑翔机的水动力分析与表示。
由图 11 可知,当滑翔机的攻角为 ± 7°时,其升阻比达到最大值 5.2,而大多数采用平板翼,其升阻比最大值小于或等于 4,远小于本滑翔机的最大升阻比。因此,海鸥一号所采用的 NACA 翼型有更好的水动力性能,使滑翔机的运动性能得到提升。

|
图 12 “海鸥一号”千岛湖湖试 Fig. 12 The Qiandao lake experiments |
由表 2 结果可以发现,与试验结果进行比较,大多数的水动力系数误差小于 10%。其中误差最大的水动力系数为KM0,可以发现与其他水动力系数数值相比其数值较小,因而当数值出现微小的变化时对误差影响较大,但并不影响实际工程上的应用。因此,本文所采用的 CFD 数值仿真方法具有较高的精度,相比于试验节省经费适合水下滑翔机水动力系数前期设计计算和工程应用。
此外,“海鸥一号”相继完成了拖曳试验和湖泊试验,但未进行回转操纵性试验。文献[12]中的水下滑翔机外形和尺寸与“海鸥一号”相似,两者的回转水动力系数在同一数量级,证明了本文所用的添加动量源项方法不仅适用于潜艇旋臂试验的模拟,也适用于水下滑翔机的回转运动的模拟。同时“海鸥一号”在千岛湖湖泊试验中顺利完成多个锯齿运动和回转运动,也进一步验证了本文所求得的粘性水动力系数满足工程应用精度。图 12 和图13 分别是千岛湖湖泊试验照片和滑翔机做锯齿运动时由压力传感器采集的信息所转换成深度随时间变化的曲线。

|
图 13 “海鸥一号”锯齿运动水深变化曲线 Fig. 13 The depth of glider in sawtooth motion |
本文介绍了实验室研制的“海鸥一号”水下滑翔机的外形,利用 CFD 软件对滑翔机斜航运动进行数值计算,并与拖曳试验结果作对比;同时通过添加动量源项结合边界条件设定的方法对滑翔机回转运动进行数值计算,并与相似滑翔机的结果进行比较,得到以下结论:
1)“海鸥一号”使用的外形具有优良的水动力性能,其中通过将天线置于尾舵中以达到减少附体阻力的效果,所使用的回转体外形曲线配合 NACA 翼型较大多数滑翔机配合平板翼在升阻比方面有了很大的提升。对以后水下滑翔机的设计和优化有一定的指导和借鉴意义。
2)本文采用 RNGk-ε 湍流模型模拟海鸥一号的斜航运动,同时利用结构化网格和非结构化网格,预报结果与拖曳试验相比,偏差较小,具有一定的工程实用价值,为水下滑翔机的前期设计和工程求解提供了指导。
3)本文采用 SSTk-ω 湍流模型模拟海鸥一号的定常回转运动,使用 Fluent 软件的 UDF 分别添加动量源项和设置边界条件完成仿真,其结果与相似外形的滑翔机结果进行对比,结果在同一数量级。此外,在湖试中“海鸥一号”也顺利实现锯齿运动和螺旋下潜运动,证明该方法同样适用于水下滑翔机。
| [1] | 叶效伟. 水下滑翔机设计、优化及运动模拟[D].上海交通大学, 2013. |
| [2] | 范双双. 洋流影响下的水下滑翔机动力学建模、运动分析与控制器设计研究[D]. 浙江大学, 2013. |
| [3] |
李志伟, 崔维成. 水下滑翔机水动力外形研究综述[J]. 船舶力学, 2012, 16(7): 831–832.
LI Zhi-wei, CUI Wei-cheng. Overview on the hydrodynamic performance of underwater gliders, [J]. Journal of Ship Mechanics, 2012, 16(7): 831–832. |
| [4] | SHERMAN J, DAVIS RE, OWENS WB, et al. " The autonomous underwater glider ‘Spray, ’” [C]// IEEE Journal of Oceanic Engineering, 2001, 26(4):437–446. |
| [5] | WEBB D C, SIMONETTI P J, and JONES C P, SLOCUM: an underwater glider propelled by environmental energy, [C]// IEEE Journal of Oceanic Engineering, 2001, 26(4):447–452. |
| [6] | ERIKSEN C C, OSSE T J, LIGHT R D, et al. Seaglider: a long-range autonomous underwater vehicle for oceanographic research, [C]// IEEE Journal of Oceanic Engineering, 2001, 26(4):424–436. |
| [7] | 王蕾. 太阳能水下滑翔机器人载体的水动力计算[D]. 沈阳: 沈阳工业大学, 2014. |
| [8] | 诸敏. 水下滑翔机设计优化与运动分析[D]. 杭州: 浙江大学, 2007. |
| [9] | CAO Jun-jun, CAO Jun-liang, YAO Bao-heng, et al. Three dimensional model, hydrodynamics analysis and motion simulation of an underwater glider, [C]// IEEE OCEANS, Genova, 2015. |
| [10] | 郑力铭. 流体计算从入门到精通[M]. 北京: 电子工业出版社, 2015. |
| [11] |
肖昌润, 刘瑞杰, 许可, 等. 潜艇旋臂回转试验数值模拟[J]. 江苏科技大学学报, 2014, 28(4): 314–315.
XIAO Chang-run, LIU Rui-jie, XU Ke, et al. Simulation for submarine rotating-arm tests [J].Journal of Jiangsu University of Science and Technology, 2014, 28(4): 314–315. |
| [12] | ZHANG Shao-wei, YU Jiang-cheng, ZHANG Ai-qun, et al. Spiraling motion of underwater gliders: Modeling, analysis, and experimental results [J]. Ocean Engineering. 2013(60): 1–13. |
 2017, Vol. 39
2017, Vol. 39
