2. 西北工业大学 航海学院,陕西 西安 710072
2. School of Marine Science and Technology, Northwestern Polytechnical University, Xi′an 710072, China
我国属世界海洋大国,拥有近 300 万平方千米的“海洋国土”。随着我国海洋战略的制定和实施,维护海洋权益的任务日益繁重,需要更多现代化的海洋装备。其中,无人水下航行器(UUV)作为一种海上力量倍增器,有着广泛而重要的军事用途,已成功用于执行扫雷、侦察、情报搜集及海洋探测等任务[1]。目前,美国、俄罗斯、欧洲等海洋强国正在加强相关研究,其技术发展的重点之一是新型水下能源动力系统,以求大幅提高无人水下航行器的航程、航深和隐蔽性[2]。
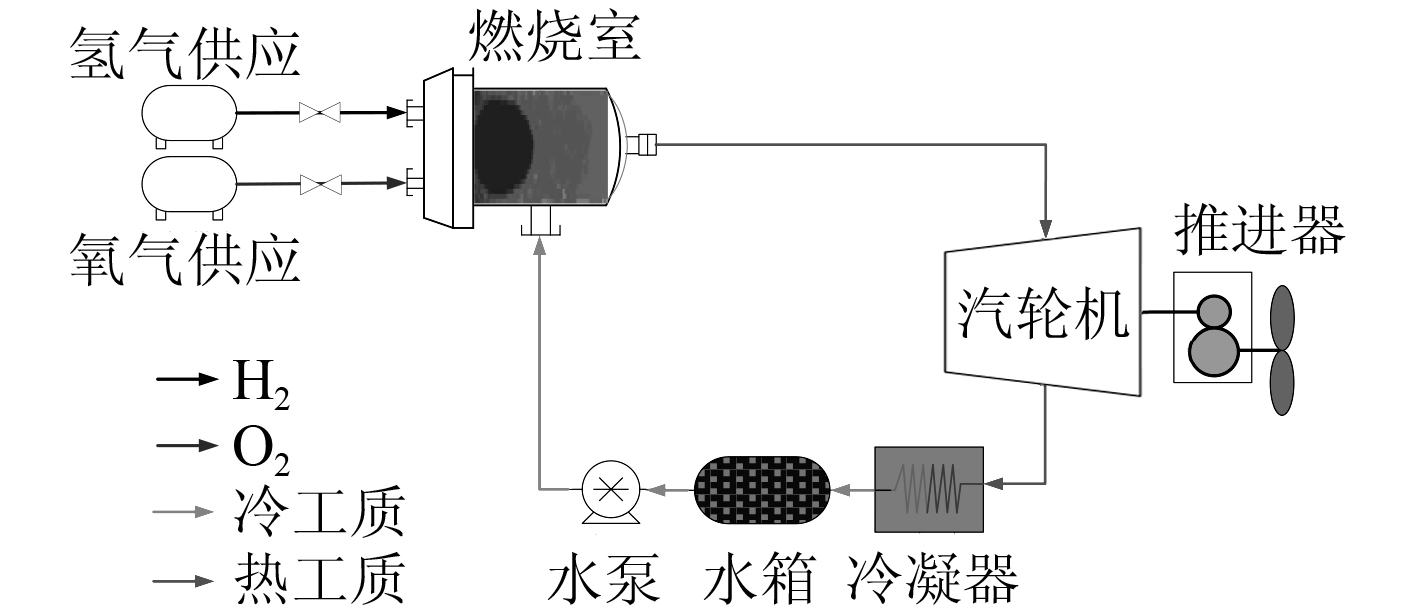
美国洛克希德公司提出了一种极具潜力的水下闭式循环动力系统设想[3],其原理如图 1 所示。该系统利用氢氧燃烧所释放的巨大热量作为其能量来源。由于氢氧完全燃烧的温度高达 3 000 K,远超过大部分材料的承受极限,因此该系统采用直接向燃烧室内喷入冷却水的方式进行冷却降温。另一方面,冷却水在燃烧室的高温条件下转化为水蒸气,与氢氧燃烧所生成的水蒸汽共同推动汽轮机做功。做功后的乏汽经冷凝器凝结为液态水后进入水箱储存,再由循环水泵增压后重新注入燃烧室。
|
图 1 水下闭式循环动力系统原理图 Fig. 1 Schematic of the underwater closed-loop propulsion system |
本文首次针对该新型水下闭式循环动力系统建立其动态数学模型,该模型主要包括加湿燃烧室、汽轮机和壳体冷凝器 3 部分。利用该模型对系统动态过程进行数值模拟,仿真结果为制定系统解耦控制策略提供了依据。
1 加湿燃烧室模型氢气和氧气在加湿燃烧室中发生燃烧反应大量放热并生成过热水蒸汽。另一方面,为确保燃烧室内部温度不超过材料所能承受的极限,冷却水从燃烧室壁喷入进行降温,这也是加湿燃烧室与常规燃烧室的主要差异所在。因此,建立加湿燃烧室数学模型需要综合考虑气相和液相动态。
1.1 气相模型由质量守恒定律可知,单位时间内燃烧室内增加的气体质量为:
| $\frac{{{\rm d}{m_c}}}{{{\rm d}t}} = \frac{{{\rm d}{m_{{{\rm H}_2}}}}}{{{\rm d}t}} + \frac{{{\rm d}{m_{{{\rm O}_2}}}}}{{{\rm d}t}} + \frac{{{\rm d}{m_{{{\rm H}_2}{\rm O}(l),in}}}}{{{\rm d}t}} - \frac{{{\rm d}{m_{c,{\rm out}}}}}{{{\rm d}t}}{\text{,}}$ | (1) |
式中:
点火后燃烧室的尾部喷管处于临界状态,因此其出口工质流量为:
| $\frac{{{\rm d}{m_{c,{\rm out}}}}}{{{\rm d}t}} = {A_e}{p_c}{(\frac{2}{{k + 1}})^{\frac{1}{{k - 1}}}}\sqrt {\frac{{2k}}{{{R_g}T(k + 1)}}}{\text{,}} $ | (2) |
式中:pc 为燃烧室压力;Ae 为喷嘴有效面积;Rg 为燃烧室内混合气体的气体常数;k 为比热比。
由能量守恒定律可知燃烧室内气体吸收的热量全部用于其内能的增加:
| ${\rm d}{U_c} = {\rm d}{Q_{\rm react}} - {\rm d}{Q_{{H_2}O(l),zf}}\text{,}$ | (3) |
式中:
| ${\rm d}{U_c} = {C_v}{m_c}{\rm d}{T_c} + {C_v}{T_c}{\rm d}{m_c}{\text{,}}$ | (4) |
将式(4)代入式(3)可得燃烧室内气体平均温度随时间的变化率为:
| $\frac{{{\rm d}{T_c}}}{{{\rm d}t}} = (\frac{{{\rm d}{Q_{\rm react}}}}{{{\rm d}t}} - \frac{{{\rm d}{Q_{{{\rm H}_2}{\rm O}(l),zf}}}}{{{\rm d}t}} - \frac{{{c_v}T{\rm d}{m_{\rm out}}}}{{{\rm d}t}})/({m_c}\times{c_v})\text{。}$ | (5) |
式中Cv 为燃烧室内混合气体的平均定压比热容。
上述燃烧室气相模型需联合气体状态方程进行综合解算,本文选用 SHBWR 状态方程描述燃烧室内真实气体状态[4]。
1.2 液相模型液相模型主要用于描述燃烧室内液体质量和温度随时间的变化率。由质量守恒可知燃烧室内液相质量随时间的变化率:
| $\frac{{{\rm d}{m_{{{\rm H}_2}{\rm O}(l),c}}}}{{{\rm d}t}} = \frac{{{\rm d}{m_{{{\rm H}_2}{\rm O}(l),{\rm in}}}}}{{{\rm d}t}} - \frac{{{\rm d}{m_{{{\rm H}_2}{\rm O}(l),zf}}}}{{{\rm d}t}}\text{。}$ | (6) |
式中:
液滴的蒸发过程可分为预热阶段和稳定蒸发阶段。在预热阶段,液滴温度不断上升;当其上升至饱和温度后,液滴温度保持不变,达到稳定蒸发阶段。对于预热阶段和稳定蒸发阶段,液滴蒸发的质量分别可用下两式描述:
| $\frac{{{\rm d}{m_{{{\rm H}_2}{\rm O}(l),c}}}}{{{\rm d}t}} \!=\! N\pi {d_l}{\rho _l}{D_l}Sh\ln (1 + Yw/(1 - Yw)){T_l} \!<\! {T_d}{\text{,}}$ | (7) |
| $ \frac{{{\rm d}{m_{{{\rm H}_2}{\rm O}(l),c}}}}{{{\rm d}t}} \!=\! N\pi {{d}_l}{\lambda _l}Nu\ln (1 \!+\! {c_p}({T_l} - {T_d})/{q_e})/{c_p} {T_l} \!\!=\!\! {T_d}{\text{。}}\!\!\!\!\!\!\!\!$ | (8) |
式中:N 为液滴总数;dl 为液滴平均粒径;ρl 为液滴密度;Dl 为液滴蒸汽扩散速率;Sh 为舍伍德数;Yw 为水滴表面的蒸汽质量份数;当水滴在过热蒸汽中蒸发时有Yw =pw/ρl,其中pw 为液滴温度对应的饱和蒸汽压;λl 为过热蒸汽的导热系数;Nu 为努塞尔数;cp 为过热蒸汽的定压比热容;qe 为单位质量液滴蒸发吸热量;Td 为液滴饱和温度。
由能量守恒可知燃烧室内液相温度随时间的变化率:
| $\begin{split}\\[-12pt]\frac{{{\rm d}{T_l}}}{{{\rm d}t}} = & (\frac{{{\rm d}{Q_{dl}}}}{{{\rm d}t}} + \frac{{{\rm d}{m_{{{\rm H}_2}{\rm O}(l),{\rm in}}}}}{{{\rm d}t}}{q_0} - \frac{{{\rm d}{m_{{{\rm H}_2}{\rm O}(l),zf}}}}{{{\rm d}t}}L)/\\ & ({m_{{{\rm H}_2}{\rm O}(l),c}}\times {c_v}){\text{,}}\end{split}$ | (9) |
式中:Tl 和Cv 分别为燃烧室内液相的平均温度和定容比热容;dQdl 为液相对流换热量;q0 为喷入单位质量的冷却水升温至Tl 所吸收的热量;L 为液相的蒸发潜热。
2 汽轮机模型汽轮机的动态特性主要取决于转子的转动惯性与汽室的容积惯性,因此动态建模中需要重点考虑。对于汽轮机的汽室,其质量守恒方程为:
| $\frac{{{\rm d}({\rho _s}{V_t})}}{{{\rm d}t}} = {m_{t,{\rm in}}} - {m_{t,{\rm out}}}{\text{,}}$ | (10) |
式中:ρs 为蒸汽密度;Vt 为汽轮机汽室体积;mt, in 为汽轮机进汽量,mt, out 为汽轮机排汽量。
能量守恒方程为:
| $\frac{{{\rm d}({\rho _s}{V_t}{U_s})}}{{{\rm d}t}} = {m_{t,\rm in}}{h_{t,\rm in}} - {m_{t,\rm out}}{h_{t,\rm out}} - {N_t}{\text{,}}$ | (11) |
式中:Us 为蒸汽的内能;ht, in 为汽轮机进口蒸汽焓值;ht, out 为汽轮机出口蒸汽焓值;Nt 为汽轮机的功率。
汽轮机的理论功即为最大可用等焓降,可用下式确定:
| ${N_t} = \frac{k}{{k - 1}}RT_o^*\left[ {1 - {{\left( {\frac{{{p_1}}}{{p_o^*}}} \right)}^{\frac{{k - 1}}{k}}}} \right]{\text{,}}$ | (12) |
式中:k 为蒸汽的绝热指数;R 为蒸汽的气体常数;
汽轮机转子运动方程为:
| $J\frac{{{\rm d}{n^2}}}{{{\rm d}t}} = \frac{{1800}}{{{\pi ^2}}}({N_t} - {N_g}){\text{。}}$ | (13) |
式中:J 为汽轮机转子的转动惯量;n 为转子的转速;Ng 为水泵所消耗的功率。
3 壳体冷凝器模型由于水下应用的特殊要求,该系统采用壳体冷凝器,即冷凝器布置在水下航行器的壳体内从而构成一个有机整体,其功能是利用壳体外部海水对汽轮机的乏汽进行冷却。壳体冷凝器中存在过热区、饱和区和过冷区 3 个相区,其尺寸约束关系为:
| ${L_{cd,l}} = {L_{cd}} - {L_{cd,b}} - {L_{cd,g}}{\text{,}}$ | (14) |
式中Lcd
,
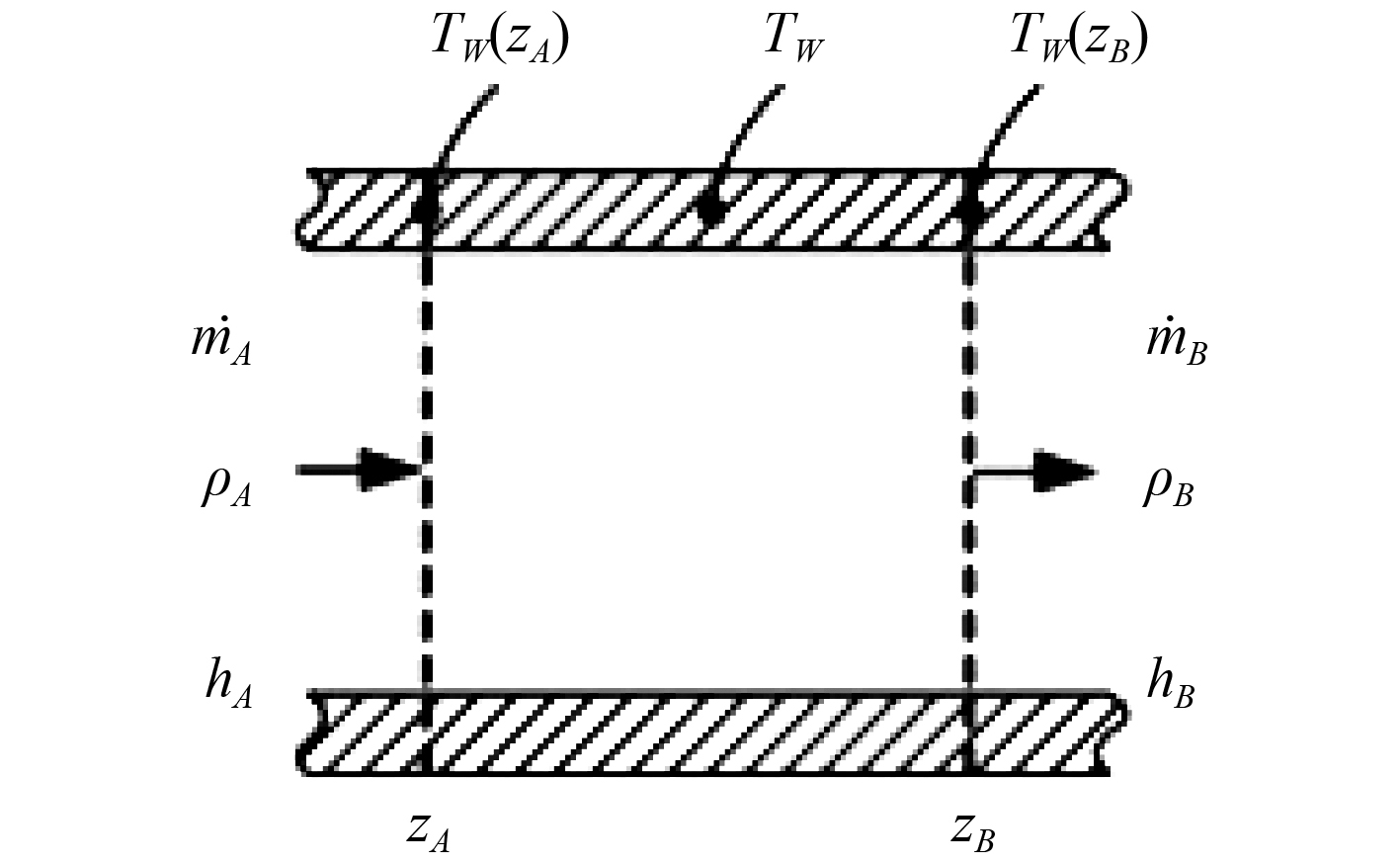
为建立冷凝器的数学模型,考察如图 2 所示的基本控制体,其中长度变量ZA 和ZB 是时间的函数。
|
图 2 控制体示意图 Fig. 2 Control unit of the shell-integrated condenser |
对于沿z 方向、通过定截面积Ω 的截面ZA (t)和ZB (t)的换热问题,其质量守恒方程为:
| $\Omega \frac{\rm d}{{{\rm d}t}}\int_{{z_A}}^{{z_B}} {\rho {\rm d}z} {\rm{ + }}{\rho _A}\varOmega \frac{{{\rm d}{z_A}}}{{{\rm d}t}} - {\rho _B}\varOmega \frac{{{\rm d}{z_B}}}{{{\rm d}t}} = {\dot m_A} - {\dot m_B}{\text{,}}$ | (15) |
能量守恒方程为:
| $\begin{split}\\[-12pt]\Omega \frac{\rm d}{{{\rm d}t}} & \int_{{z_A}}^{{z_B}} {\left( {h\rho } \right){\rm d}z} - \varOmega {h_B}{\rho _B}\frac{{{\rm d}{z_B}}}{{{\rm d}t}} + \varOmega {h_A}{\rho _A}\frac{{{\rm d}{z_A}}}{{dt}} - \\& \varOmega \left( {{z_B} - {z_A}} \right)\frac{{{\rm d}p}}{{{\rm d}t}} = {h_A}{\dot m_A} - {h_B}{\dot m_B} + q\left( {{z_B} - {z_A}} \right){\text{。}}\end{split}$ | (16) |
将
| $\begin{split}\displaystyle \frac{\rm d}{{{\rm d}t}}\int_{{L_{cd,g}} + {L_{cd,b}}}^{{L_{cd}}} {\rho dz} {\rm{ + }}\rho \frac{{{\rm d}({L_{cd,g}} + {L_{cd,b}})}}{{{\rm d}t}}-\\[8pt] \quad \quad \rho \displaystyle\frac{{{\rm d}{L_{cd}}}}{{{\rm d}t}} = {{\dot m}_{cd,bout}} - {{\dot m}_{cd,out}} = 0{\text{。}}\end{split}$ | (17) |
式中:
将
| ${equation}{18}\begin{aligned}{A_{cd}}\displaystyle\frac{\rm d}{{{\rm d}t}}\!\! & \int_{{L_{cd,g}} \!+\! {L_{cd,b}}}^{{L_{cd}}} \!\!{\left( {{\rho _{cd,lsa}}h} \right){\rm d}z} \!\!+\!\! {A_{cd}}{h_{cd,lsa}}{\rho _{cd,lsa}}\displaystyle\frac{{{\rm d}\left( {{L_{cd,g}} \!\!+\!\! {L_{cd,b}}} \right)}}{{{\rm d}t}}\!=\\ & \displaystyle {h_{cd,lsa}}{{\dot m}_{cd,\rm bout}} - {h_{cd,\rm out}}{{\dot m}_{cd,out}} + {q_{cd,l}}{L_{cd,l}}{\text{。}}\quad\quad\quad (18)\end{aligned}$ |
式中:Acd
为冷凝器的截面积;
定义过冷区的平均比焓为:
| ${h_{cd,lav}} = \frac{{\left( {{h_{cd,\rm out}} + {h_{cd,lsa}}} \right)}}{2}{\text{。}}$ | (19) |
式中:
则式(18)左边第一项改写为:
| $\begin{aligned}\frac{\rm d}{{{\rm d}t}}& \int_{{L_{cd,g}} + {L_{cd,b}}}^{{L_{cd}}} {\left( {{\rho _{cd,lsa}}h} \right){\rm d}z} = {\rho _{cd,lsa}}\frac{{{\rm d}{h_{cd,lav}}{L_{cd,l}}}}{{{\rm d}t}} =\\ & {\rho _{cd,lsa}}\left( {{h_{cd,lav}}\frac{{{\rm d}{L_{cd,l}}}}{{{\rm d}t}} + \frac{{{L_{cd,l}}}}{2}\frac{{{\rm d}{h_{cd,\rm out}}}}{{{\rm d}t}}} \right){\text{。}}\end{aligned}$ | (20) |
将式(20)代入式(18)中,则过冷区的能量守恒方程可写为:
| ${a_b}\frac{{{\rm d}{L_{cd,b}}}}{{{\rm d}t}} + {a_g}\frac{{{\rm d}{L_{cd,g}}}}{{{\rm d}t}} + {a_h}\frac{{{\rm d}{h_{cd,\rm out}}}}{{{\rm d}t}} = {a_q}{\text{,}}$ | (21) |
式中:
将
| $\begin{aligned}\!\!\!\!\!{A_{cd}}\displaystyle\frac{\rm d}{{{\rm d}t}} & \int_{{L_{cd,g}}}^{{L_{cd,g}} + {L_{cd,b}}} {\rho dz} {\rm{ + }}{\rho _{cd,gsa}}{A_{cd}}\frac{{{\rm d}{L_{cd,g}}}}{{{\rm d}t}}-\\& {\rho _{cd,lsa}}{A_{cd}}\frac{{{\rm d}\left( {{L_{cd,g}} + {L_{cd,b}}} \right)}}{{{\rm d}t}} \!= \!{{\dot m}_{cd,gout}} \!-\! {{\dot m}_{cd,bout}}{\text{。}}\end{aligned}$ | (22) |
式中:
定义饱和区的平均密度为:
| ${\rho _{cd,gav}} = {\gamma _{cd,av}}{\rho _{cd,gsa}} + \left( {1 - {\gamma _{cd,av}}} \right){\rho _{cd,lsa}}{\text{。}}$ | (23) |
式中
则式(22)左边第 1 项可化为:
| $\begin{aligned} \frac{\rm d}{{{\rm d}t}}& \int_{{L_{cd,g}}}^{{L_{cd,g}} + {L_{cd,b}}} {\rho {\rm d}z} = \frac{{{\rm d}\left( {{\rho _{cd,gav}}{L_{cd,b}}} \right)}}{{{\rm d}t}} =\\& \left[ {{\gamma _{cd,av}}{\rho _{cd,gsa}} + \left( {1 - {\gamma _{cd,av}}} \right){\rho _{cd,lsa}}} \right]\frac{{{\rm d}{L_{cd,b}}}}{{{\rm d}t}}{\text{。}} \end{aligned}$ | (24) |
将式(24)代入式(22)中,则饱和区的质量守恒方程可写为:
| ${b_b}\frac{{{\rm d}{L_{cd,b}}}}{{{\rm d}t}} + {b_g}\frac{{{\rm d}{L_{cd,g}}}}{{{\rm d}t}} - \frac{{{{\dot m}_{cd,\rm gout}}}}{{{A_{cd}}}} = {b_q}\text{。}$ | (25) |
式中:
将
| $\begin{split}\\[-12pt]{A_{cd}} & \displaystyle\frac{\rm d}{{{\rm d}t}}\int_{{L_{cd,g}}}^{{L_{cd,g}} + {L_{cd,b}}} {\left( {h\rho } \right){\rm d}z} + {A_{cd}}{h_{cd,gsa}}{\rho _{cd,gsa}}\displaystyle\frac{{{\rm d}{L_{cd,g}}}}{{{\rm d}t}}-\\& {A_{cd}}{h_{cd,lsa}}{\rho _{cd,lsa}}\displaystyle\frac{{{\rm d}\left( {{L_{cd,g}} + {L_{cd,b}}} \right)}}{{{\rm d}t}}=\\ & {h_{cd,gsa}}{{\dot m}_{cd,\rm gout}} - {h_{cd,lsa}}{{\dot m}_{cd,\rm bout}} + {q_{cd,b}}{L_{cd,b}}{\text{,}}\end{split}$ | (26) |
式(26)左边第一项可化为:
| $\begin{aligned} \frac{d}{{dt}}& \displaystyle\int_{{L_{cd,g}}}^{{L_{cd,g}} + {L_{cd,b}}} {\left( {h\rho } \right){\rm d}z} = \\& \left[ {{\gamma _{cd,av}}{\rho _{cd,gsa}}{h_{cd,gsa}} + \left( {1 - {\gamma _{cd,av}}} \right){\rho _{cd,lsa}}{h_{cd,lsa}}} \right]\frac{{{\rm d}{L_{cd,b}}}}{{{\rm d}t}}{\text{。}} \end{aligned}$ | (27) |
将式(27)代入式(26)中,则饱和区的能量守恒方程可写为:
| ${c_b}\frac{{{\rm d}{L_{cd,b}}}}{{{\rm d}t}} + {c_g}\frac{{{\rm d}{L_{cd,g}}}}{{{\rm d}t}} - \frac{{{h_{cd,gsa}}}}{{{A_{cd}}}}{\dot m_{cd,g{\rm out}}} = {c_q}{\text{。}}$ | (28) |
式中:
将
| ${A_{cd}}\frac{\rm d}{{{\rm d}t}}\int_0^{{L_{cd,g}}} {\rho dz} \!-\! {\rho _{cd,gsa}}{A_{cd}}\frac{{{\rm d}{L_{cd,g}}}}{{{\rm d}t}} \!=\! {\dot m_{cd,{\rm in}}} \!- \!{\dot m_{cd,g{\rm out}}}{\text{。}}$ | (29) |
式中
定义过热区的平均密度为:
| ${\rho _{cd,gav}} = \frac{{({\rho _{cd,\rm in}} + {\rho _{cd,gsa}})}}{2}{\text{,}}$ | (30) |
式中
则式(30)左边第一项可写为:
| $\begin{split}\\[-12pt]\frac{{\rm{d}}}{{{\rm{d}}t}}\int_0^{{L_{cd,g}}} \rho dz = & \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {{\rho _{cd,gav}}{L_{cd,g}}} \right) = \\ & \frac{{{L_{cd,g}}}}{2}\frac{{{\rm{d}}{\rho _{cd,{\rm{in}}}}}}{{{\rm{d}}t}} + {\rho _{cd,gav}}\frac{{{\rm{d}}{L_{cd,g}}}}{{{\rm{d}}t}}{\text{。}}\end{split}$ | (31) |
过热区的进口工质密度即为汽轮机气室工质密度,由式(10)可知:
| $\frac{{{\rm d}{\rho _{cd,\rm in}}}}{{{\rm d}t}} = \frac{{{{\dot m}_{t,{\rm in}}} - {{\dot m}_{cd,\rm in}}}}{{{V_t}}}{\text{。}}$ | (32) |
式中:
将式(32)代入式(31)中,则过热区的质量守恒方程可写为:
| ${{ d}_g}\frac{{{\rm d}{L_{cd,g}}}}{{{\rm d}t}} + \frac{{{{\dot m}_{cd,\rm gout}}}}{{{A_{cd}}}} + {d_m}{\dot m_{cd,\rm in}} = {d_q}{\text{。}}$ | (33) |
式中:
将
| $\begin{aligned} {A_{cd}}\displaystyle \frac{\rm d}{{{\rm d}t}}& \int_0^{{L_{cd,g}}} {\left( {h\rho } \right){\rm d}z} - {A_{cd}}{h_{cd,gsa}}{\rho _{cd,gsa}}\displaystyle \frac{{{\rm d}{L_{cd,g}}}}{{{\rm d}t}} =\\& {h_{cd,in}}{\dot m_{cd,\rm in}} - {h_{cd,gsa}}{\dot m_{cd,\rm gout}} + {q_{cd,g}}{L_{cd,g}}{\text{。}}\end{aligned}$ | (34) |
定义过热区的平均比焓为:
| ${h_{cd,gav}} = \frac{{({h_{cd,\rm in}} + {h_{cd,gsa}})}}{2}{\text{,}}$ |
式中
则式(34)左边第一项可写为:
| $\begin{split}\\[-12pt] \frac{{\rm{d}}}{{{\rm{d}}t}}\int_0^{{L_{cd,g}}} & {\left( {h\rho } \right){\rm{d}}z} = \frac{{{\rm{d}}\left( {{\rho _{cd,gav}}{h_{cd,gav}}{L_{cd,g}}} \right)}}{{{\rm{d}}t}}\\& {\rho _{cd,gav}}{h_{cd,gav}}\frac{{{\rm{d}}{L_{cd,g}}}}{{{\rm{d}}t}} + \frac{{{L_{cd,g}}}}{{2{V_{tr}}}} \times \qquad\qquad\qquad\quad (35)\\ & \left\{ {\left[ {\frac{{{\rho _{cd,gav}}}}{{{\rho _{cd,{\rm{in}}}}}}\left( {{h_{tr}} - {h_{cd,{\rm{in}}}}} \right) + {h_{cd,gav}}} \right]{{\dot m}_n} - {h_{cd,gav}}{{\dot m}_{cd,\rm in}}} \right\}{\text{。}}\end{split}$ |
将式(35)代入式(34)中,则过热区的能量守恒方程可写为:
| ${e_g}\frac{{{\rm d}{L_{cd,g}}}}{{{\rm d}t}} + \frac{{{h_{cd,gsa}}}}{{{A_{cd}}}}{\dot m_{cd,\rm gout}} + {e_m}{\dot m_{cd,\rm in}} = {e_q}{\text{。}}$ | (36) |
式中:
| ${e_g} = {\rho _{cd,gav}}{h_{cd,gav}} - {\rho _{cd,gsa}}{h_{cd,gsa}}{\text{,}}$ | (37) |
| ${e_m} = - \left( {\frac{{{L_{cd,g}}{h_{cd,gav}}}}{{2{V_{tr}}}} + \frac{{{h_{cd,\rm in}}}}{{{A_{cd}}}}} \right){\text{,}}$ | (38) |
| ${e_q}\!\! =\!\!\! \frac{{{q_{cd,g}}{L_{cd,g}}}}{{{A_{cd}}}}\!\! -\!\! \frac{{{L_{cd,g}}}}{{2{V_t}}}\!\!\left[ {\frac{{{\rho _{cd,gav}}}}{{{\rho _{cd,in}}}}\!\!\left( {{h_{tr}} \!\!-\!\! {h_{cd,\rm in}}} \right) \!\!+\!\! {h_{cd,gav}}} \right]{\dot m_n}{\text{。}}$ | (39) |
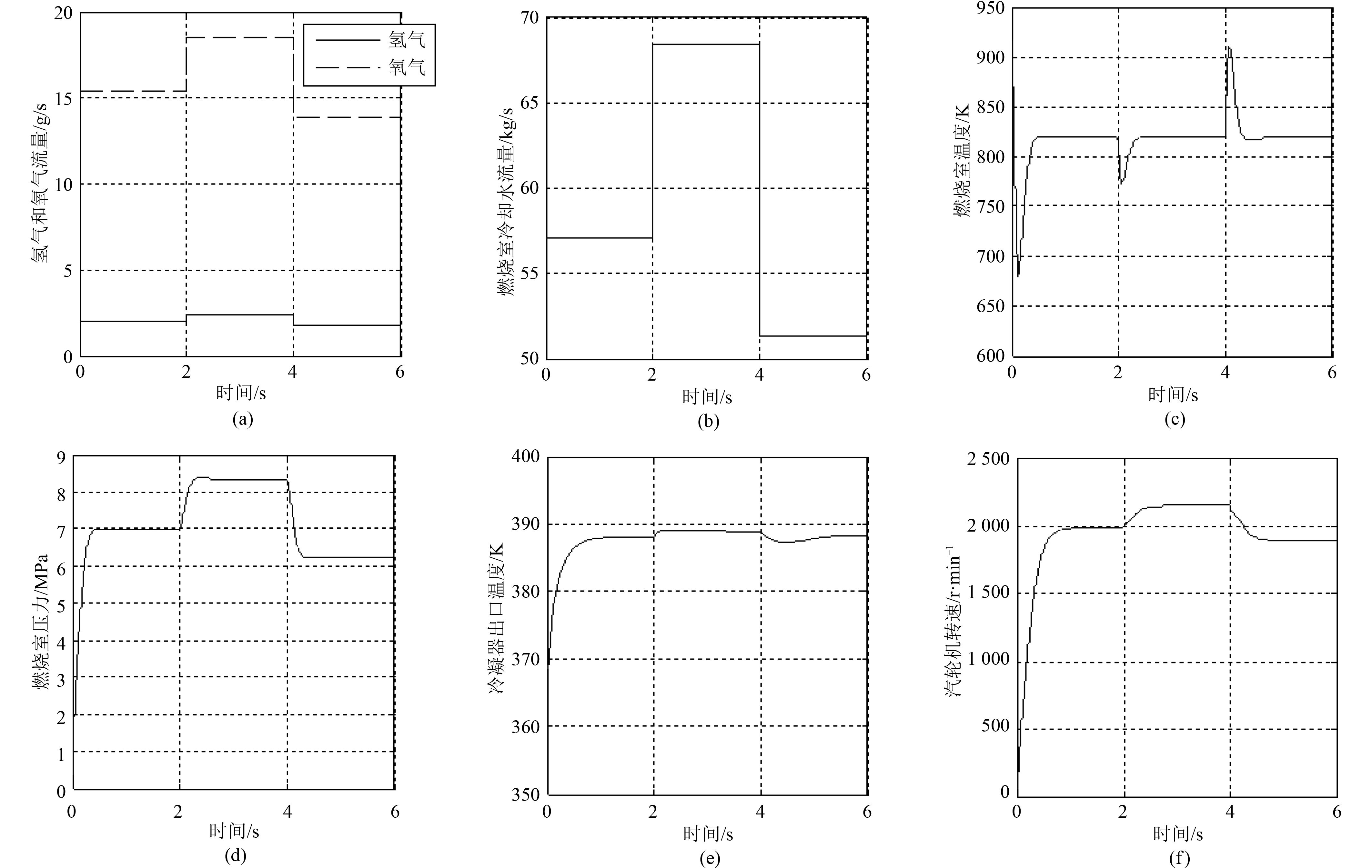
本文利用上述模型对该水下闭式循环动力系统变工况过程进行仿真,以获得系统的动态特性,从而为制定系统控制策略提供依据。仿真时,设置模型的 3 个输入参数氢气流量、氧气流量和燃烧冷却水量同步阶跃变化,如图 3(a)和图 3(b)所示。需要说明的是,氢气流量和氧气流量在阶跃变化前后始终保持化学反应方程所确定的比例关系;另一方面,冷却水流量在阶跃变化前后也与氢、氧气流量保持特定比例关系。利用模型仿真获得系统关键热力参数的变化规律,包括燃烧室压力、燃烧室温度、冷凝器出口温度以及汽轮机转速,如图 3(c)~图 3(f)所示。
|
图 3 系统仿真结果 Fig. 3 Simulation results |
由图 3(c)可知,燃烧室温度由于冷却水的注入在初始阶段有大幅的下降,随着掺混水的加热蒸发,燃烧室温度也逐渐达到稳态值;而当 3 个输入参数阶跃变化时,燃烧室温度表现出明显的波动,但随后仍能维持原来的稳态值,这主要是由于氢、氧气和冷却水流量在在阶跃变化前后始终保持系统热平衡所确定的比例关系。另一方面,由图 3(e)可知燃烧室压力在 3 个输入参数阶跃变化时呈现出相同趋势的变化,这是由于燃烧室压力主要取决于进入燃烧室的工质量。由于冷凝器具有较大的热惯性,导致其出口温度变化较慢,幅度也不如燃烧室温度明显,如图 3(e)所示。由图 3(f)可知,汽轮机转速随燃烧室压力增减而升降,这是由于汽轮机转速主要取决与燃烧室的压力和温度,在燃烧室温度基本不变的条件下,燃烧室压力的变化决定了汽轮机输出功率和转速的变化。
根据上述变工况仿真结果,我们提出新型水下闭式循环动力系统的解耦控制策略,即同步调节氢气流量、氧气流量和冷却水流量,并确保三者始终保持系统热平衡所确定的比例关系,使燃烧室温度基本保持不变,通过改变燃烧室压力调节汽轮机输出功率,也即实现燃烧室温度-压力的解耦控制。
5 结 语本文建立了新型水下闭式循环动力系统的动态模型,通过仿真获得了系统压力、温度、转速等关键参数的变化规律。仿真结果表明,氢、氧气和冷却水流量同步阶跃变化,且变化前后始终满足燃烧室热平衡所确定的比例关系,燃烧室和冷凝器的温度基本能维持在设计点附近,而燃烧室压力和汽轮机输出功率的动态过程将只取决于系统工质总流量的变化。该仿真结果为制定系统解耦控制策略奠定了基础。
| [1] |
兰志林, 周家波. 无人水下航行器发展综述[J]. 国防科技, 2008, 29(2): 11–15.
LAN Zhi-lin, ZHOU Jia-bo. An overview of development of unmanned underwater vehicles[J]. National Defense Science and Technology, 2008, 29(2): 11–15. |
| [2] |
王晓武, 林志民, 崔立军. 无人潜水器及其动力系统技术发展现状及趋势分析[J]. 舰船科学技术, 2009, 31(8): 31–34.
WANG Xiao-wu, LIN Zhi-min, CUI Li-jun. Analysis of technology status and development trend for unmanned underwater vehicle and its propulsion system. Ship Science and Technology, 2009, 31(8): 31–34. |
| [3] | GOLDMEER J S, GIRODET W H, Closed-Loop cooling system for a hydrogen/oxygen based combustor[P]. US: 7178339 B2, 2007-02-20. |
| [4] |
朱灵峰, 杜磊, 李新宝, 等. 生物质合成甲醇的热力学性质研究[J]. 太阳能学报, 2009, 30(2): 256–260.
ZHU Ling-feng, DU Lei, LI Xin-bao. Thermodynamic property study of methanol synthesis from biomass[J]. Acta Energiae Solaris Sinca, 2009, 30(2): 256–260. |
 2017, Vol. 39
2017, Vol. 39
