由于船舶电力系统负荷具有复杂性、多样性、时变性等特点,要建立准确的负荷模型并进行参数辨识是一个不易解决的难题。
若采用不准确的模型和参数,很可能导致船舶电力系统的计算分析结果与实际运行工况大相径庭,从而给系统带来不必要的浪费或潜在的隐患。在以往的船舶电力系统仿真研究中,很少深入开展综合负荷模型研究[1]。本文根据船舶电力系统负荷中感应电动机占比较大,每种特定工况下负荷时变性不明显的特点,提出一种船舶综合负荷模型(Ship Integrative Load Model,SILM),应用到船舶电力系统负荷建模研究中。
在参数辨识方法上,目前普遍采用优化类算法。文献[2]采用了遗传算法,证明该算法优于最小二乘法;文献[3]对比了粒子群算法和遗传算法,认为粒子群算法的收敛速度更快;文献[4]采用了模式搜索法,该方法数值稳定性好,但计算速度慢。
混沌优化算法是一种新型搜索算法,其基本思想是把变量从混沌空间变换到解空间,然后利用混沌变量具有遍历性、随机性和规律性的特点进行搜索[5]。文献[6]将混沌优化应用于负荷预测;文献[7]将其应用于电力系统无功优化;文献[8]将混沌优化方法应用于静态负荷的参数辨识,但目前的研究结果表明,动态负荷才是影响电力系统稳定的关键因素;文献[9]将混沌优化方法与神经网络相结合用于负荷参数辨识,但其使用的负荷模型并不是真正的考虑感应电动机的动态模型。
本文首先对现有的混沌优化算法进行改进,然后将其应用到 SILM 模型的参数辨识上。
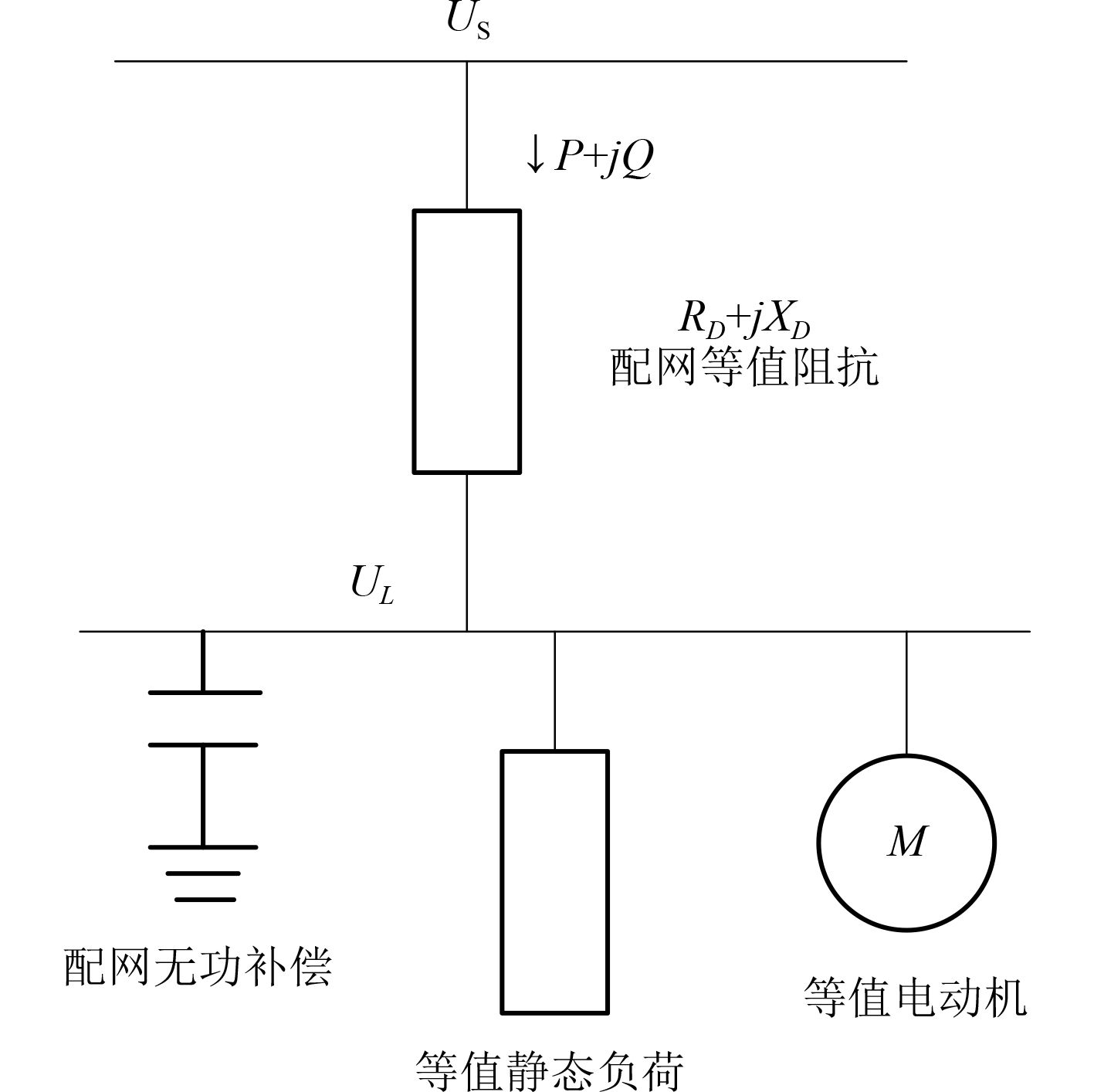
1 SILM 模型及参数辨识方法SILM 模型的结构如图 1 所示。该综合负荷模型由等值静态负荷(包括无功补偿)和等值电动机(动态负荷)并联组成。静态负荷一般只考虑恒阻抗负荷,且方程采用指数形式,因为指数形式参数较少,利于参数辨识[3]。
|
图 1 SILM 模型结构 Fig. 1 The Structure of SILM |
等值静态负荷的方程为:
| ${P_S} = {P_{S0}}{(\frac{{{U_L}}}{{{U_{L0}}}})^{{p_v}}},\quad {Q_S} = {Q_{S0}}{(\frac{{{U_L}}}{{{U_{L0}}}})^{{q_v}}}, $ | (1) |
式中:PS ,QS 为静态负荷吸收的有功,无功功率;PS0,QS0 为稳态时静态负荷吸收的有功,无功功率;UL 为动态过程中虚拟母线的电压;UL0 为虚拟母线的稳态电压;pv 和qv 为静态负荷的有功电压系数和无功电压系数。
等值电动机 3 阶暂态模型的极坐标形式为:
| $T'\frac{{{\rm{d}}E'}}{{{\rm{d}}t}} = - E' + C{U_L}\cos \delta \text{,}$ | (2) |
| $\frac{{{\rm{d}}\delta }}{{{\rm{d}}t}} = - \frac{{C{U_L}}}{{T'E'}}\sin \delta + ({\omega _r} - 1)\text{,}$ | (3) |
| $M\frac{{{\rm{d}}{\omega _r}}}{{{\rm{d}}t}} = - \frac{{{U_L}E'}}{{X'}}\sin \delta - {T_m}\text{。}$ | (4) |
式中:
感应电动机消耗的功率为:
| ${P_d} = - \frac{{{U_L}E'}}{{X'}}\sin \delta ,\quad {Q_d} = \frac{{{U_L}({U_L} - E'\cos \delta )}}{{X'}}\text{。}$ | (5) |
式中:X' 为感应电动机转子不动时短路电抗;X 为感应电动机转子开路电抗;
配网消耗功率为:
| ${P_D} = \frac{{{P^2} + {Q^2}}}{{U_S^2}}{R_D}, {Q_D} = \frac{{{P^2} + {Q^2}}}{{U_S^2}}{X_D}\text{,}$ | (6) |
其中P、Q 为 110 kV 母线的实测功率。
船舶综合负荷模型总的功率方程为:
| $P \! \! = \! \! {P_S} \! + \! {P_d} \! + \! {P_D} \! \!=\! \! {P_{S0}}{(\frac{{{U_L}}}{{{U_{L0}}}})^{{p_v}}}\! \! -\! \! \frac{{{U_L}E'}}{{X'}}\sin \delta \! +\! \! \frac{{{P^2}\! \! +\! \! {Q^2}}}{{U_S^2}}{R_D}\text{,}\! \! $ | (7) |
| $\begin{split}Q = {Q_S} + {Q_d} + {Q_D} = {Q_{S0}}{(\displaystyle\frac{{{U_L}}}{{{U_{L0}}}})^{{q_v}}} + \\[5pt]\quad \:\displaystyle\frac{{{U_L}({U_L} - E'\cos \delta )}}{{X'}} + \frac{{{P^2} + {Q^2}}}{{U_S^2}}{X_D}\text{。}\end{split}$ | (8) |
参数辨识的过程就是不断的优化综合负荷模型的参数,并根据式(7)和式(8)计算输出的有功和无功功率,将其与实测到的有功和无功响应进行对比,直到计算值与实测值的误差小于允许值为止。这就是一个多变量优化问题。
令
| $\min E \! = \! \! \sum\limits_{K = 1}^N {[{{(P(K) \! - \! {P_C}(K,\theta ))}^2} + } {(P(K) - {P_C}(K,\theta ))^2}]\text{。}$ | (9) |
其物理意义就是要求仿真得到的负荷动态响应与实测响应越接近越好。
2 混沌优化算法及其改进混沌是存在于非线性系统中的一种较为普遍的现象,混沌运动具有遍历性、随机性、规律性等特点[5]。Logistic 映射是非线性方程中出现的一个能成功进行混沌研究的实例,它最初用来描述昆虫数目的世代变化规律。Logistic 映射如下:
| ${{ x}_{n + 1}} = u{{ x}_n}(1 - {x_n}) n = 0,1,2, \cdots \text{。}$ | (10) |
其中:u 为控制参量,是一个正常数,当 3.544 090 ≤u ≤ 4 时,由任意初值x0∈(0,1),可迭代出一个混沌轨迹,其在(0,1)范围内遍历。混沌优化算法就是利用了这个遍历特性,其基本步骤如下[5]:
步骤 1 对式(10)中向量 xn 分别赋予m 个具有微小差异的初值(不能为 0.25,0.5 和 0.75),m 是需要优化的参数的个数。经过k 次迭代后可以得到m 个不同的混沌变量xi (k),i = 1…m。
步骤 2 将混沌变量xi (k)映射到优化变量的搜索空间,得到Xi (k):
| ${X_i}(k) = {c_i} + {d_i}{x_i}(k)$ | (11) |
式中:ci ,di 为常数,与变量的搜索空间 [a,b] 有关,ci =a,di =b –a。
步骤 3 第 1 次混沌优化搜索(粗搜索)。优化指标是 minf(Xi ),设f* 为当前最优解,X* 为对应的参数组合。依次将Xi (k)代入计算优化指标f(Xi (k)),如f(Xi (k))<f*,则f* =f(Xi (k)),X* =Xi (k)。否则放弃Xi (k)。直到f* 保持若干步不变后。
步骤 4 第 2 次混沌优化搜索(细搜索)。按式(12)产生新的混沌变量Xi (k′),αi 为小于 1 的控制变量。
| ${X_i}(k') = X_i^ * + {\alpha _i}({x_i}(k') - 0.5)\text{。}$ | (12) |
步骤 5 依次将Xi (k’)代入计算优化指标f(Xi (k’)),如果f(Xi (k’))<f*,则X* =Xi (k’),f* =f(Xi (k’))。否则放弃Xi (k’)。直到f* 保持若干步不变后,输出结果。
文献[10]提出一种加速混沌优化的方法,其在完成步骤 5 后以X* 为中心,缩小搜索范围再次进行混沌优化(步骤 1 ~步骤 3)。但是在比较了以往各文献中关于算法流程的描述,并进行了大量的对比测试后发现,直接在第 1 次搜索(粗搜索)的结果上将搜索范围缩小到当前值的 ±15%,再执行一次混沌优化对于缩短搜索时间更加有效,而对搜索精度只有轻微影响。以此调整算法的步骤:
新步骤 4 在步骤 3 得到的X* 基础上,将参数的搜索范围缩小到 [0.85X*,1.15X*],同时注意新的搜索范围的边界不应超越原来的搜索边界。
新步骤 5 将混沌变量xi (k)映射到新的搜索空间,得到Xi (k’):
| ${X_i}(k') = {c_i} + {d_i}{x_i}(k)\text{。}$ | (13) |
新步骤 6 内容同原步骤 5。
随后使用如下测试函数F1~F5,对文献[10]所述的加速方法和本文提出的改进算法在速度和精度上进行了对比,表 1 给出了对比结果。从中可以看出本文提出的算法在保证精度的情况下寻优速度有了很大改进。
| $F_1 = 100{(x_1^2 - {x_2})^2} + {(1 - {x_1})^2}, {x_i} \in [ - 2.048,2.048]\text{,}$ | (14) |
| $\begin{split}\\[1pt]F_2 =& [1+(x_1+x_2+1)^2(19-14x_1+3x_1^2-14x_26 +\\[2pt]& x_1x_2+3x_2^2]{\cdot}[30+(2x_1-3x_2)^2(18-32x_1 + \\[2pt]& 12x_1^2+48x_2-36x_1x_2+27x_2^2], x_i \in [-2,2]\text{,}\end{split}$ | (15) |
| $F_3 = x_1^2 + x_2^2 + x_3^2, {x_i} \in [ - 5.12,5.12]\text{,}$ | (16) |
| $F_4 = 0.5 + \frac{{{{\sin }^2}\sqrt {x_1^2 + x_2^2} - 0.5}}{{{{[1.0 + 0.001(x_1^2 + x_2^2)]}^2}}}, {x_i} \in [ - 5,5]\text{,}$ | (17) |
| $\begin{split}\\F_5 =& |4 - 2.1x_1^2 +\! x_1^4/3| + {x_1}{x_2} + (4x_2^2 - 4)x_2^2, \\[2pt]& {x_i} \in [ - 5,5]\text{。}\end{split}$ | (18) |
|
|
表 1 本文改进算法与文献[10]中算法的比较 Tab.1 The comparison between the improved algorithm and the algorithm in the literature [10] |
仿真算例的有功和无功动态响应曲线是根据已知的电压扰动和负荷初始功率直接由式(1)~式(8)计算所得。随后以式(9)作为优化指标,采用本文提出的改进混沌优化算法对该综合负荷模型进行参数辨识。
1)两参数(PMP 、KL )优化结果
对 SILM 模型中的 2 个参数进行优化,迭代初值取随机数,表 2 给出了连续优化 10 次的结果。从表中可以看出,优化结果比较满意。
|
|
表 2 2 个参数连续优化 10 次的结果 Tab.2 Two parameters for 10 successive optimization results |
2)三参数(PMP ,KL ,XD )优化结果
对 SILM 模型中的 3 个参数进行优化,表 3 给出了连续优化 10 次的结果。从表中拟合误差一列可以看出,优化效果相比 2 个参数时略差,通过试验表明,即使迭代次数增加 10 倍,依然不能有效改善这种情况。原因是多增加一个参数使得寻优空间结构的复杂程度大大增加所致。在这种情况下,搜索范围越小的参数越容易找到真值。
|
|
表 3 3 个参数连续优化 10 次的结果 Tab.3 Three parameters for 10 successive optimization results |
3)四参数(PMP ,XS ,KL ,XD )优化结果
对 SILM 模型中的 4 个参数进行优化,迭代初值取随机数,表 4 给出了连续优化 10 次的结果。虽然 4 参数优化的拟合误差大于 3 参数和 2 参数的优化结果,但是各参数优化值与真实值的绝对误差已经很小了,可以满足工程应用的需要。
|
|
表 4 4 个参数连续优化 10 次的结果 Tab.4 Four parameters for 10 successive optimization results |
本文提出了一种改进的混沌优化算法,较以往的混沌优化算法在寻优的速度上有明显的优势,在寻优精度上与以往的方法相当。在将其应用到 SILM 模型参数辨识的过程中,通过仿真分析还得到了以下结论:参数优化的精度总体上随需要优化的参数数目的增加而降低,但搜索范围小的参数受影响小,因此合理缩小参数的寻优范围对提高优化算法的精度有非常积极的作用。总的来说,本文提出的改进混沌优化算法可以用于辨识船舶综合负荷模型的参数,并且在速度和精度上都有满意的效果。
| [1] | 王新枝, 夏立, 张超. 考虑负荷动态模型的船舶电力系统暂态电压稳定分析[J]. 中南大学学报自然科学版), 2014, 45(7): 2231–2236. |
| [2] | 朱守真, 沈善德, 郑宇辉, 等. 负荷建模和参数辨识的遗传进化算法[J]. 清华大学学报(自然科学版), 1999, 39(3): 37–40. |
| [3] | 程颖, 鞠平, 吴峰. 负荷模型参数辨识的粒子群优化法及其与基因算法比较[J]. 电力系统自动化, 2003, 27(11): 25–29. |
| [4] | 王进, 李欣然, 苏盛. 一种电力系统综合负荷模型辨识的改进算法研究[J]. 电力系统及其自动化学报, 2002, 14(2): 12–15. |
| [5] | 李兵, 蒋慰孙. 混沌优化方法及其应用[J]. 控制理论与应用, 1997, 14(4): 613–615. |
| [6] |
李天云, 刘自发. 电力系统负荷的混沌特性及预测[J]. 中国电机工程学报, 2000, 20(11): 36–40.
LI Tian-yun, LIU Zi-fa. The Chaotic property of power load and its forecasting [J]. Proceedings of CSEE, 2000, 20(11): 36–40. |
| [7] | 刘宝英, 杨仁刚, 李慧, 等. 基于混沌遗传算法的电力系统无功优化[J]. 电力系统及其自动化学报, 2006, 18(5): 49–52. |
| [8] | 唐巍, 郭镇明, 李殿璞. 混沌优化用于电力系统静态负荷模型参数辨识[J]. 电力系统自动化, 2000, C24(13): 27–30. |
| [9] | 姚建刚, 陈亮, 戴习军, 等. 混沌神经网络负荷建模的理论研究[J]. 中国电机工程学报, 2002, 22(3): 99–102. |
| [10] |
李旲, 胡云昌, 曹宏铎. 加速混沌优化方法及其应用[J]. 系统工程学报, 2002, 17(1): 41–44.
LI Ying, HU Yun-chang, CAO Hong-duo. Stepped-up chaos optimization algorithm and its application [J]. Journal of Systems Engineering, 2002, 17(1): 41–44. |
 2017, Vol. 39
2017, Vol. 39
