2. 船舶振动噪声重点实验室,湖北 武汉 430033
2. National Key Laboratory on Ship Vibration and Noise, Wuhan 430033, China
通常来说机械振动是有害的,如果不加以控制和消除,会对人员和环境造成不良影响。所以,减振降噪成为了许多机械设备在设计阶段考虑的问题。振动的分析预测与评估日渐为工程人员所重视。在工程实践中,针对各种不同的情况和问题有许多指标可以来评判振动控制的效果。而在船舶工程领域,常采用振级落差来评定实际系统的振动控制效果[1]。但是,这种评估方式并不完善,不能完全反应振动的传递特性,存在着一定的缺陷。而振动功率流兼顾了力和速度 2 个参数,从能量传递的角度来研究振动控制问题更加科学合理。振动能量是系统内振动传递的本质,由于系统内的力或者速度响应均为能量传递的一种表现,因此以振动能量为基础研究系统的振动传递特性正是传递本质的反映[2]。功率可以由力和速度的乘积获得,不仅描述了能量转移或者转化的快慢程度,而且可用于表征振动能量在系统内的流动情况。应用功率流方法研究系统的振动传递问题具有许多优点,且切实可行。本文使用振动功率流来研究四边简支薄板上的单层隔振系统的振动特性,采用不同的指标对隔振效果进行评估,探讨不同参数的变化对单层隔振系统的隔振效果的影响,比较不同的隔振效果评价指标之间的关系。
1 弹性基础上单层隔振系统的功率流分析 1.1 隔振效果的评估在评价振动时,可以采用不同的指标。如在判断空气中传播声音的强度时,可采用声压,也可采用声强。所以在评价隔声效果时,可采用声压级或者声强级的差值进行评价。对比空气中传播声音的评价指标可发现,功率流概念与声学中的声功率相对应,而功率流密度则与声强相对应。
在工程研究中,通常采用振级落差和插入损失来评价隔振系统的隔振效果[3]。在计算振级落差和插入损失时,可以采用不同的参数,例如位移、速度、加速度等。考虑到工程实际中的传感器多为加速度传感器,所以多用加速度来计算振级落差和插入损失。根据加速度计算出来的振级落差和插入损失,称为加速度振级落差和加速度插入损失。所以当考虑用功率流来评估隔振效果时,可以类比得到功率流的振级落差和功率流的插入损失。但功率流的振级落差这种说法并不准确,因为功率流表示的是能量在隔振系统中传递的情况,并不存在振级这种说法,所以称之为功率流落差更为准确。
若激励力F(t)和响应v(t)均为简谐,可以记
| $P(\omega ) = \frac{\omega }{{2{\pi} }}\int_0^{2{\pi}/\omega } {{\mathop{\rm Re}\nolimits} \left\{ F \right\} \cdot {\mathop{\rm Re}\nolimits} \left\{ v \right\}{\rm d}t} = \frac{1}{2}\left| F \right|\left| v \right|\cos \varphi \text{,}$ | (1) |
或
| $P = \frac{1}{2}{\mathop{ {\rm R}e}\nolimits} \left\{ {F{v^ * }} \right\} = \frac{1}{2}{\mathop{\rm Re}\nolimits} \left\{ {{F^ * }v} \right\}\text{,}$ | (2) |
其中F* 和v* 分别为F 和v 的共轭复函数。若记M 为结构在F 作用点处的导纳,则功率流又可表示为:
| $P = \frac{1}{2}{\left| F \right|^2}{\mathop{\rm Re}\nolimits} \left\{ M \right\} = \frac{1}{2}{\left| v \right|^2}{\mathop{\rm Re}\nolimits} \left\{ {\frac{1}{M}} \right\}\text{。}$ | (3) |
所以,如果知道了力或者速度的幅值以及隔振系统的导纳矩阵,那么就可以算出功率流。
振级落差的定义为被隔振设备振动响应的有效值与对应基础响应的有效值之比的常用对数的 20 倍,其表达式为:
| ${L_D} = 20\lg \frac{{{v_1}}}{{{v_2}}}\text{。}$ | (4) |
而插入损失定义为采取隔振措施前后基础响应的有效值之比的常用对数的 20 倍,其表达式[5]为:
| ${L_I} = 20\lg \frac{{{v_R}}}{{{v_2}}}\text{,}$ | (5) |
类比振级落差和插入损失进行推导,得到功率流落差为:
| ${D_p} = 10\lg \frac{{{P_{in}}}}{{{P_{tr}}}}\text{,}$ | (6) |
式中:Pin 为振源输入到整个系统的功率流;Ptr 为通过隔振器进入到基础结构的功率流。同样可以得到功率流插入损失为
| ${I_p} = 10\lg \frac{{{P_u}}}{{{P_{tr}}}}\text{。}$ | (7) |
式中,Pu 为没有隔振器时传递到基础结构的功率流,Ptr 为安装有隔振器时通过隔振器进入到基础结构的功率流。
1.2 模型分析在船舶工程领域,许多隔振系统属于柔性基础上的单层隔振系统。为了方便研究,将其简化为四边简支薄板上的单层隔振系统模型(见图 1)[6]。通过对该模型的分析,可以考察系统各结构参数对振动控制效果的影响,为隔振系统的设计提供指导。
在该模型中,机器视为刚体,基础为四边简支矩形薄板,支撑系统由 4 个相同的隔振器组成,隔振器质量忽略不计,且隔振器与基础板为点接触。
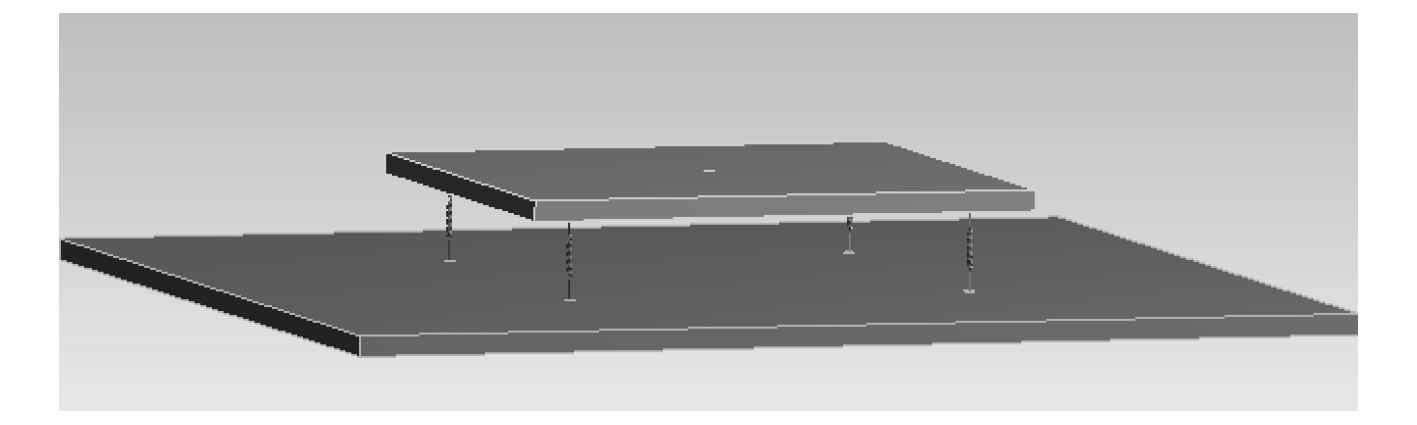
|
图 1 单层隔振系统模型 Fig. 1 Single vibration isolation system model |
根据定义和系统假设,有
| ${\bf{\varepsilon }} \!\!=\!\! \left\{ {{\varepsilon _1},{\varepsilon _2},{\varepsilon _3},{\varepsilon _4},{\varepsilon _5},{\varepsilon _6}|{\varepsilon _3}\!\! = \!\!1,{\varepsilon _5}\!\! = \!\!\frac{{\left| {{T_y}} \right|}}{{\left| {{f_z}} \right|}}{e^{i\varphi }},{\varepsilon _{1,2,4,6}} \equiv 0} \right\}\text{。}\!\!\!\!\!\!\!\!\!\!$ | (8) |
根据系统的结构特点,可以导出机器导纳矩阵、支撑系统四端参数矩阵、基础结构导纳矩阵等系统结构参量矩阵。
由于机器被视为刚体,可得机器的导纳矩阵为:
| ${{A}} = \left[ {\begin{array}{*{20}{c}}{{{{A}}_{11}}} & {{{{A}}_{12}}}\\{{{{A}}_{21}}} & {{{{A}}_{22}}}\end{array}} \right]\text{。}$ | (9) |
式中, A 11 为机器在质心的广义点导纳矩阵; A 12 和 A 21 分别为机器由界面与各支撑联结点到质心的广义传递导纳矩阵和由质心到界面各支撑联结点的广义传递导纳矩阵; A 22 为机器在界面上与各支撑联结点的广义点导纳矩阵:
系统中的隔振支撑为理想隔振器,忽略其质量,假设隔振器在沿Ox,Oy,Oz 正交方向上的复刚度分别为
| ${{{B}}_{11}} = {{{B}}_{22}} = {{E}}\text{,}$ | (10) |
| ${{{B}}_{12}} = {\bf{0}}\text{,}$ | (11) |
| ${{{B}}_{21}} ={\rm diag}(\frac{{i\omega }}{{{K_x}}},\frac{{i\omega }}{{{K_x}}},\frac{{i\omega }}{{{K_y}}},\frac{{i\omega }}{{{K_y}}},\frac{{i\omega }}{{{K_z}}},\frac{{i\omega }}{{{K_z}}})\text{。}$ | (12) |
若只考虑垂向振动,可以得到基础结构的导纳矩阵:
| ${{{M}}_F} = \left[ {\begin{array}{*{20}{c}}{{{{M}}_{Fxx}}} & {{{{M}}_{Fxy}}} & {{{{M}}_{Fxz}}}\\{{{{M}}_{Fyx}}} & {{{{M}}_{Fyy}}} & {{{{M}}_{Fyz}}}\\{{{{M}}_{Fzx}}} & {{{{M}}_{Fzy}}} & {{{{M}}_{Fzz}}}\end{array}} \right]\text{,}$ | (13) |
其中:
| $\begin{aligned}& {{{M}}_{Fxx}} = {{{M}}_{Fxy}} = {{{M}}_{Fxz}} = {{{M}}_{Fyx}} = {{{M}}_{Fyy}} =\\& \quad\quad\quad\ {{{M}}_{Fyz}} = {{{M}}_{Fzx}} = {{{M}}_{Fzy}} = {{0}}{\text{,}}\end{aligned}$ | (14) |
| ${{{M}}_{Fzz}} = \left[ {\begin{array}{*{20}{c}}{{m_{Fz{z_{11}}}}} & {{m_{Fz{z_{12}}}}}\\{{m_{Fz{z_{21}}}}} & {{m_{Fz{z_{22}}}}}\end{array}} \right]\text{,}$ | (15) |
| $\begin{aligned}{m_{Fz{z_{jk}}}} = & \frac{{4i\omega }}{{\rho hab}}\sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {\frac{{{\varphi _{mn}}({h_j},b/2) \cdot {\varphi _{mn}}({h_k},b/2)}}{{{\omega _{mn}}^2(1 + i\delta )}}} } \\& (j,k = 1,2)\text{。}\end{aligned}$ | (16) |
式中:ρ、h、δ 分别为基础板的密度、厚度和阻尼比;φmn 、ωmn 分别为四边简支矩形薄板的振型函数和无阻尼自由振动时的固有频率。
上述参数可以较为完备地描述整个振动系统的动态结构特征。
对于机器与基础,可以写出作用在其上面的力与速度响应的关系
| $\left[ {\begin{array}{*{20}{c}}{{{{v}}_O}}\\{{{{v}}_I}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{{{{A}}_{11}}} & {{{{A}}_{12}}}\\{{{{A}}_{21}}} & {{{{A}}_{22}}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{{{F}}_e}}\\{{{{F}}_I}}\end{array}} \right]\text{,}$ | (17) |
根据隔振器的四端参数关系,可以得到
| $\left[ {\begin{array}{*{20}{c}}{{{{F}}_I}}\\{{{{v}}_I}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{{{{B}}_{11}}} & {{{{B}}_{12}}}\\{{{{B}}_{21}}} & {{{{B}}_{22}}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{{{F}}_F}}\\{{{{v}}_F}}\end{array}} \right]\text{。}$ | (18) |
根据上面 2 式可推得传递到到基础的功率流为:
| $\begin{aligned}{P_{tr}}\!\!= & \!\!\frac{1}{2}{\mathop{\rm Re}\nolimits} \left\{ {{{({{{F}}_F})}^H} \!\cdot\! {{{v}}_F}} \right\}\!\! =\!\! \\ & \frac{1}{2}{\mathop{\rm Re}\nolimits} \left\{ {{{({{{F}}_e})}^H} \!\cdot \!\left[ {{{({{{T}}_I})}^H} \!\cdot\! {{{M}}_F} \!\cdot\! {{{T}}_I}} \right]\! \cdot\! {{{F}}_e}} \right\}\text{,}\end{aligned}$ | (19) |
可以得出系统功率流传递矩阵为
| ${{{X}}_I} = {({{{T}}_I})^H} \cdot {{{M}}_F} \cdot {{{T}}_I}\text{。}$ | (20) |
那么
| ${P_{tr}} = \frac{1}{2}{\mathop{\rm Re}\nolimits} \left\{ {{{({{{F}}_e})}^H} \cdot {{{X}}_I} \cdot {{{F}}_e}} \right\}\text{。}$ | (21) |
根据上式可以看出,Ptr 是关于 Fe 和 XI 的函数,由 Fe 和 XI 所决定。
2 功率流数值仿真通过数值计算对四边简支薄板上的单层隔振系统进行数值仿真,采用功率流这个指标对隔振效果进行评估,改变不同的参数,观察其对隔振效果的影响。与工程上常用的加速度振级落差和插入损失进行对比分析。
|
|
表 1 控制变量计算隔振效果 Tab.1 Vibration reduction effect calculation by different variable |
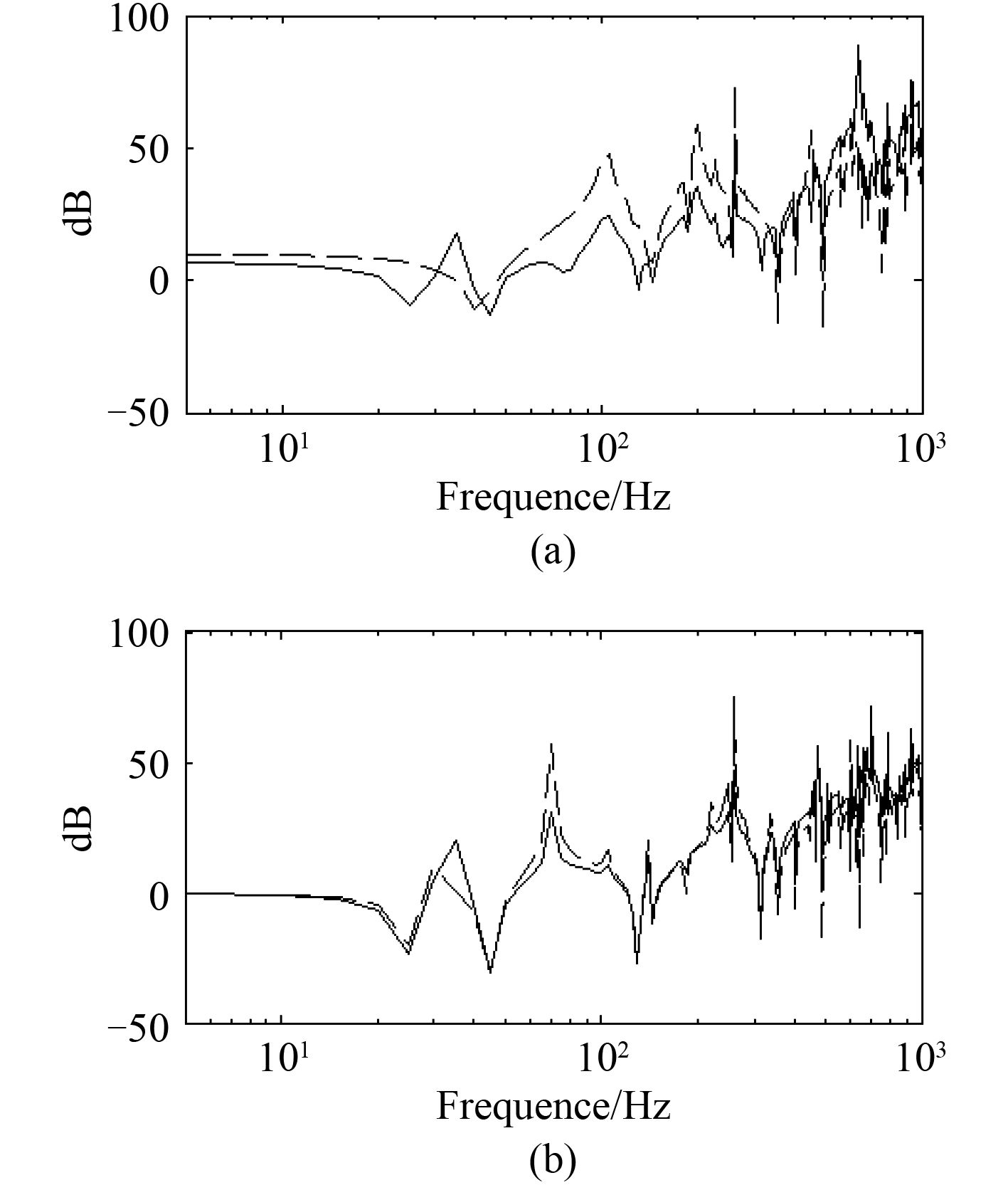
以隔振器的刚度为 2 000 N/mm,基础板的宽为 2 m,基础板的厚度为 20 mm,支撑间距为 0.8 m 的模型作为参考,通过改变不同的参数,来观察四端简支薄板上的单层隔振系统的振动传递特性。
|
图 2 参考的隔振系统 Fig. 2 Reference vibration isolation system |
图 2为参考模型的隔振效果曲线,其中图2(a)中的实线表示功率流落差Dp ,虚线表示加速度振级落差LD ;图2(b)中的实线表示功率流的插入损失Ip ,虚线表示隔振系统的加速度插入损失LI 。在图2(b)的隔振效果图中,也采用相同的画图方式。
观察图 2 可以发现,四边简支单层隔振系统对于低频振动的隔振效果要差一些。功率流落差Dp 和加速度振级落差LD 在变化趋势上具有相当的相似性,频域的峰值在位置上具有一定的一致性。功率流插入损失和加速度插入损失的变化趋势也具有相当的相似性。但是,随着频率升高,Dp 和IP 的值升高得更快。理论上功率流落差应该总是为正,但是在图中可以发现存在功率流落差为负值的点,这是因为在计算功率流时,我们采用的是垂向的位移和垂向的力,而总的功率流是 3 个自由度上的总和,这使得在某些频率上尽管总功率流是正值,但垂向的功率流却是负值[7]。
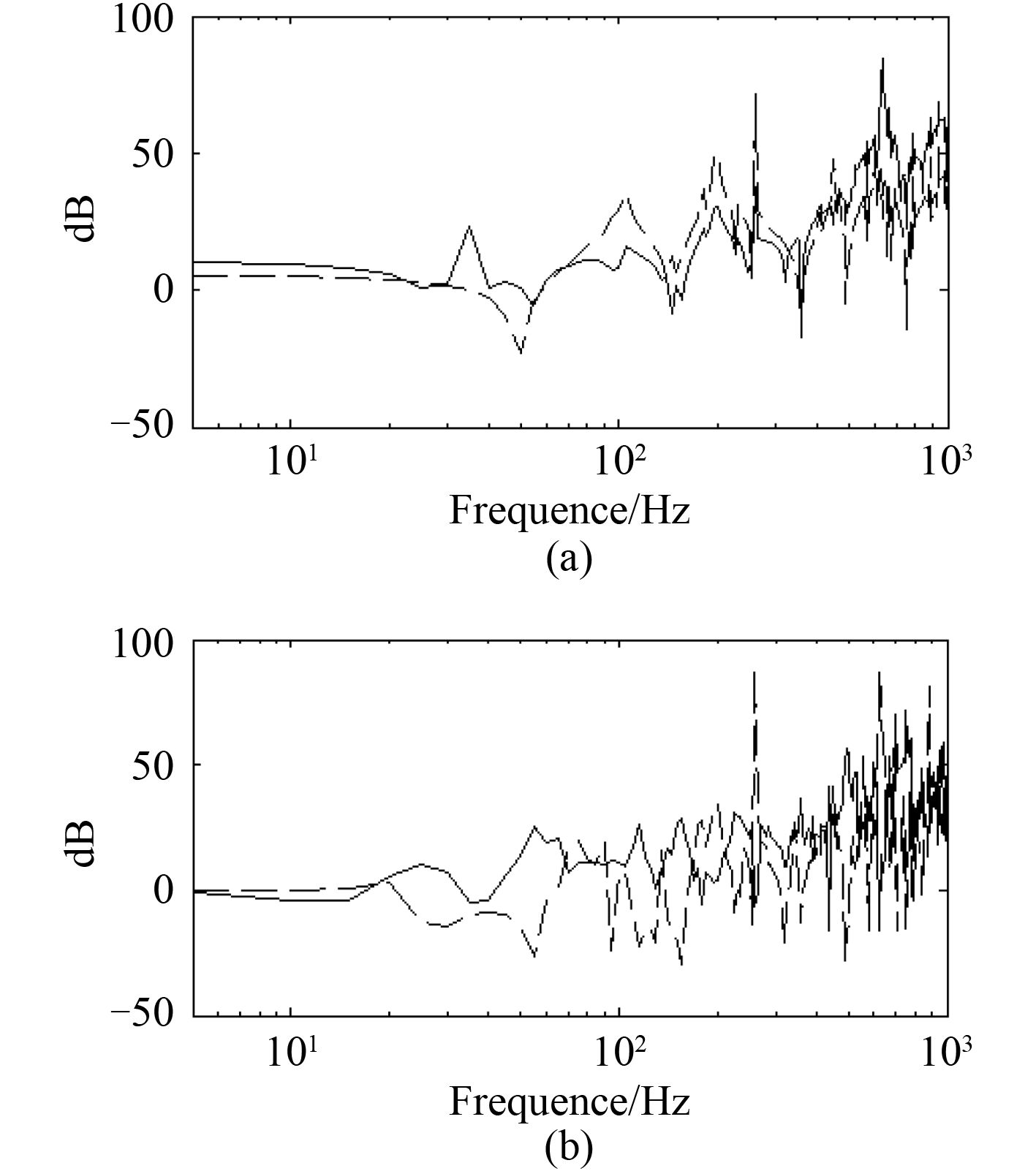
|
图 3 隔振器刚度对隔振效果的影响 Fig. 3 Effect of the vibration isolator stiffness |
图 3是将隔振器刚度从 2 000 N/mm 改为 5 000 N/mm 之后的隔振效果曲线。刚度增加以后,隔振效果有所下降。
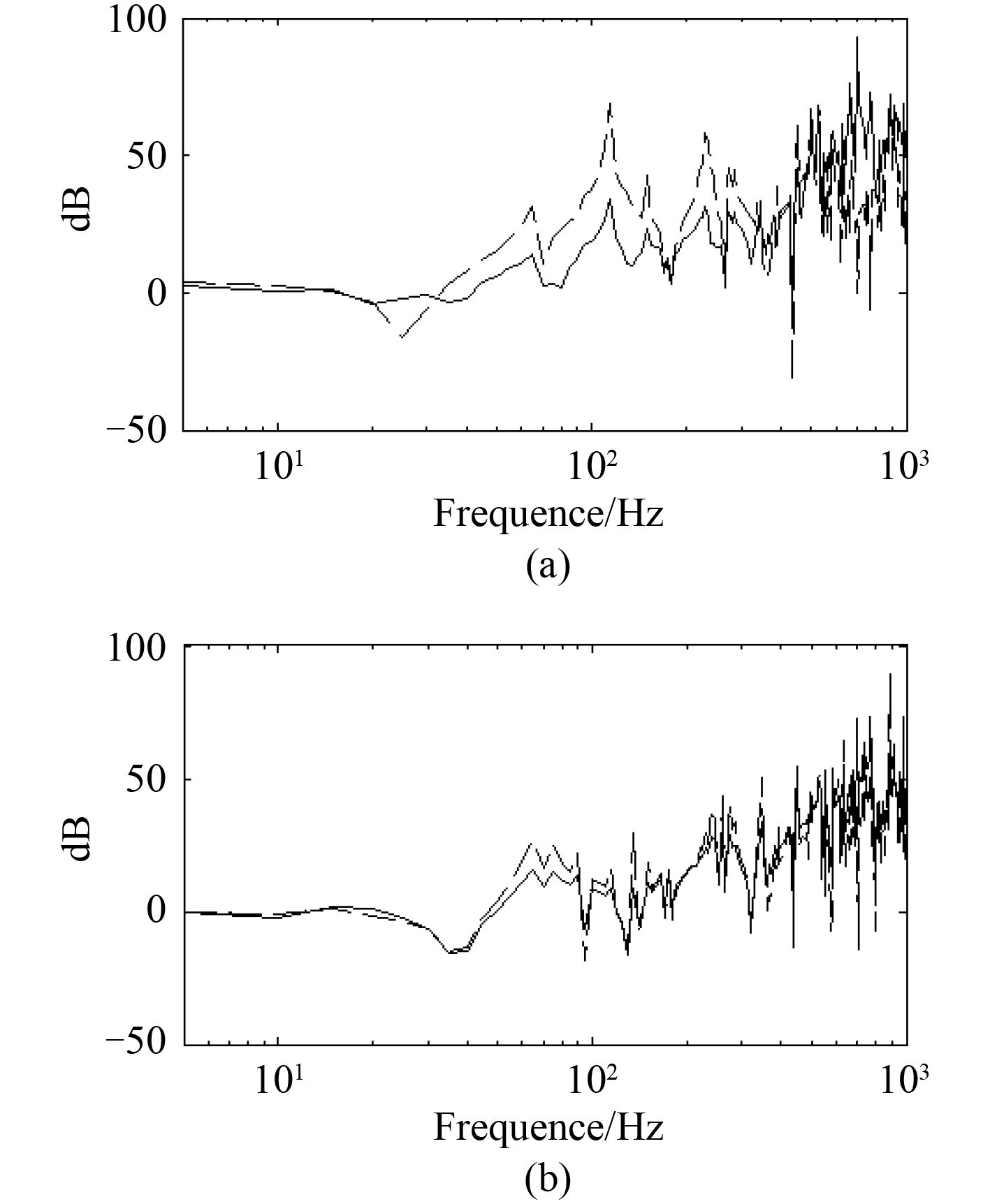
|
图 4 基础板宽对隔振效果的影响 Fig. 4 Effect of the width of plate |
图 4 为将基础板宽度从2m改为3m之后的隔振效果曲线。可以看出增加基础板的宽度之后,隔振效果有所下降。
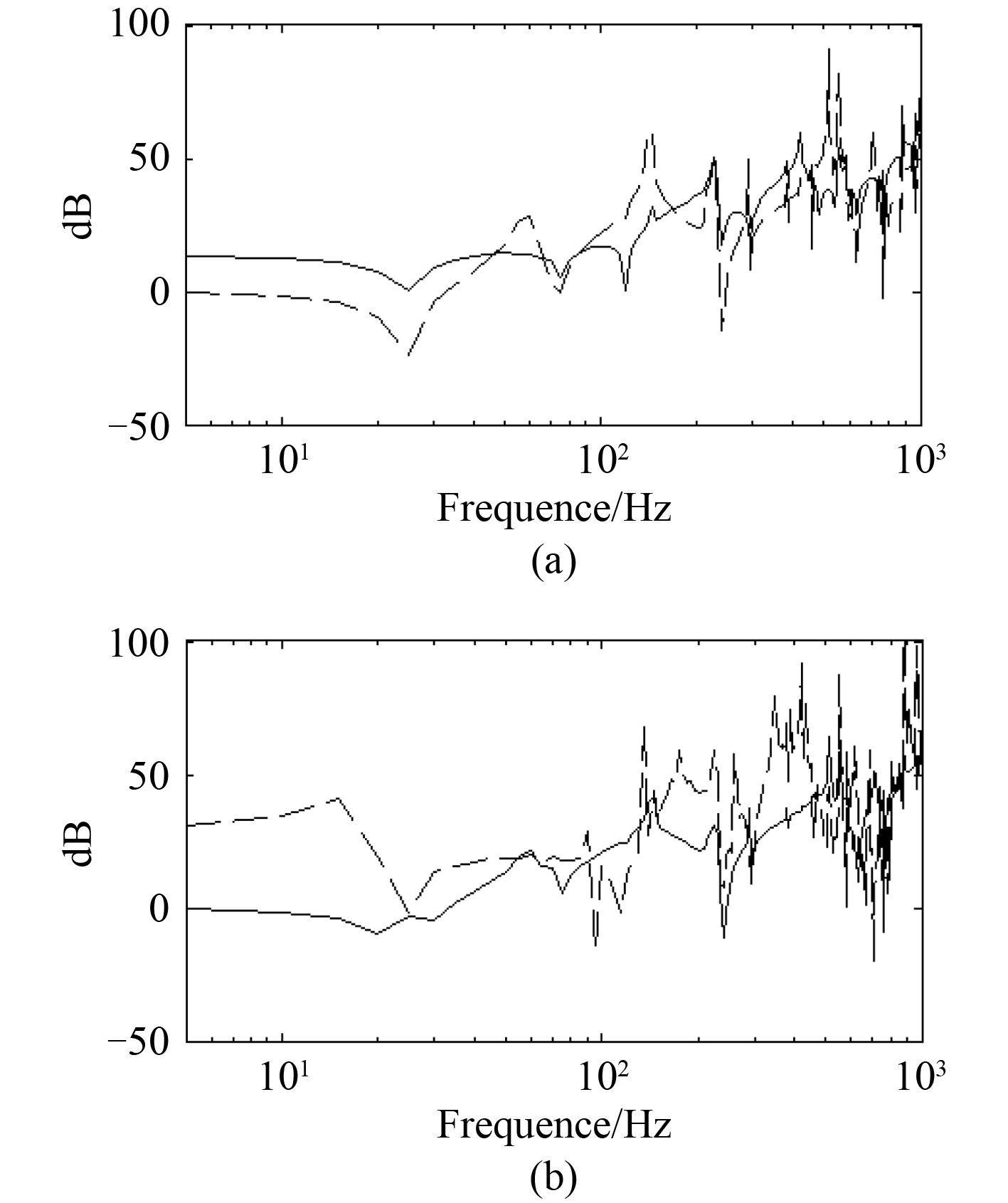
|
图 5 基础板厚度对隔振效果的影响 Fig. 5 Effect of the thickness of the plate |
图 5 为将基础板厚度从 20 mm 改为 40 mm 之后的隔振效果曲线。可以看出,增加基础板的厚度之后,隔振效果有所增强。
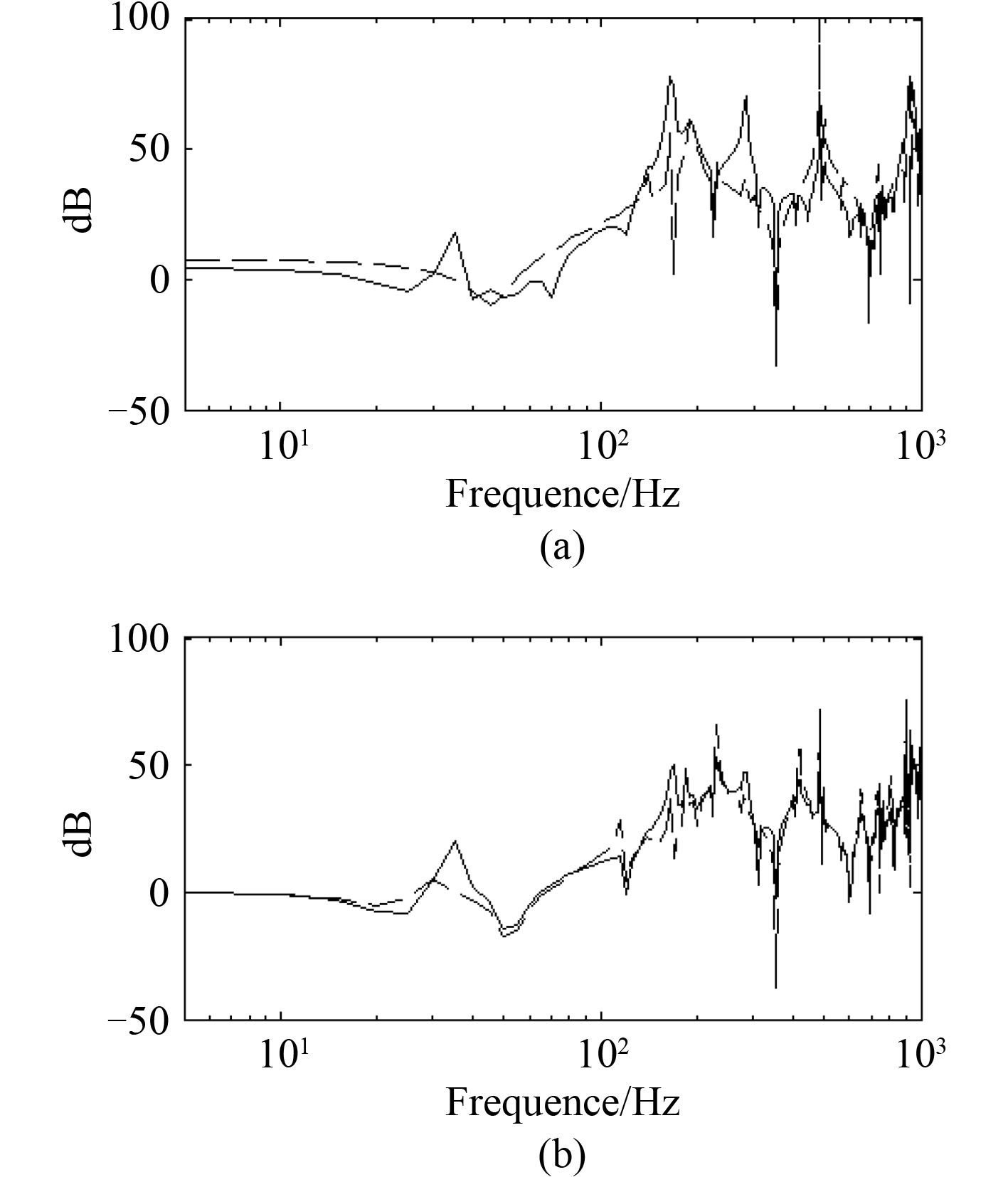
|
图 6 支撑间距对隔振效果的影响 Fig. 6 Effect of the support spacing |
图 6 为将隔振器的支撑间距从 0.8 m 改为 0.6 m 之后的隔振效果曲线。可以看出,支撑间距缩小之后,隔振效果有所下降。
根据数值分析的结果可看出,系统的隔振效率总体上取决于隔振器的刚度。隔振效率同样也受到基础弹性的影响,增加基础的刚度可以提高高阶模态的共振频率。隔振器的支撑间距的变化会使隔振系统的模态频率也发生变化,更大的支撑间距会使得隔振效率的线性计权有所改善。观察上方的图像,功率流落差Dp 、功率流的插入损失Ip 表达式,并采用数值分析的方法比较了功率流落差Dp 、加速度振级落差LD 、功率流的插入损失Ip 、加速度插入损失LI 这几种隔振效果评价指标的曲线不存在较大程度上的偏离,但是功率流的计算更大程度上的考虑了基础特性,所以功率流作为隔振设计的指标具有相当的可靠性和有效性。
3 结 语本文运用机械阻抗概念,得出四边简支板上单层隔振系统的系统结构参数矩阵,进一步推算出功率流在单层隔振系统中的传递矩阵,推算出功率流落差Dp 、功率流的插入损失Ip 表达式,并采用数值分析的方法比较了功率流落差Dp 、加速度振级落差LD 、功率流的插入损失Ip 、加速度插入损失LI 这几种隔振效果评价指标的关系。通过改变隔振器和基础板的参数,并通过有限元仿真对隔振系统进行谐响应分析。通过隔振效果的对比发现,隔振器的刚度的变化、基础板宽、基础板厚、支撑间距的变化会对隔振系统产生不同的影响。通过分析得出的结论能够对柔性基础上的单层隔振系统的优化与评估改进有一定的参考作用。
| [1] |
严济宽, 柴敏, 陈小琳. 振动隔离效果的评定[J]. 噪声与振动控制, 1997(6): 22–30.
YAN Ji-kuan, CHAI Min, CHEN Xiao-lin. Evaluation of vibration isolation efficiency[J]. Noise and Vibration Control, 1997(6): 22–30. |
| [2] | 韩旭. 车辆系统振动传递路径分析与结构声辐射控制研究[D]. 上海: 交通大学, 2013. |
| [3] | 朱石坚, 何琳. 船舶机械振动控制[M]. 北京: 国防工业出版社出版社, 2006. |
| [4] |
严济宽. 振动功率流的一般表达式及其测量方法[J]. 噪声与振动控制, 1987(1): 24–29.
YAN Ji-kuan. General expression of vibration power flow and its measurement method[J]. Noise and Vibration Control, 1987(1): 24–29. |
| [5] |
霍睿, 施引. 功率流隔振效率评价指标及其与振级落差的关系[J]. 中国造船, 2007, 48(3): 86–92.
HUO Rui, SHI Yin. The power flow efficiency criterion for vibration isolation design and its relationship with vibration level difference[J]. Shipbuilding of China, 2007, 48(3): 86–92. |
| [6] | 周保国. 复杂隔振系统的功率流研究[D]. 上海: 交通大学, 1994. |
| [7] |
乔百杰, 赵彤, 陈雪峰. 功率流测量以及振动能量参数估计试验研究[J]. 振动与冲击, 2014 (7): 194–198.
QIAO Bai-jie, ZHAO Tong, CHEN Xue-feng. Tests for power flow measurement and vibrational energy estimation[J]. Journal of Vibration and Shock, 2014(7): 194–198. |
 2017, Vol. 39
2017, Vol. 39
