船舶在航行过程中,会产生不同程度的振动,如振动系统固有振动频率与激励频率一致或接近时,会产生共振现象。而轴系回旋振动是由于螺旋桨在不均匀的伴流场中工作时,将产生周期性的弯曲力矩作用在螺旋桨轴上,激励力的简谐次数为:vp =iZp (i = 1,2,…),Zp 为螺旋桨的叶片数,主要的简谐次数为叶片次v =Zp 。推进轴系在螺旋桨或转轴上旋转的横向力矩作用下,旋转轴绕其静平衡曲线产生振动,严重的轴系回旋振动会导致尾管后轴承过热或早期过渡磨损,并导致轴承套的腐蚀、尾管密封装置漏损,还会使螺旋桨轴锥端前面键槽区域内产生附加交变弯曲应力,甚至出现龟裂、折断等疲劳破坏,另外严重的轴系回旋振动引起轴承反力的动力放大,进而引起船体尾部结构的振动,而过度的船体结构振动,除对人员的舒适性影响外,还可能引起局部结构疲劳损坏或机械设备故障,甚至影响船舶的正常航行[1]。低速大功率柴油机推进轴系,由于其 1 阶 1 次回旋振动固有频率远远高于额定转速,不会出现螺旋桨不平衡质量离心力引起的共振问题,但具有人字架的轴系其 1 阶 1 次回旋振动固有频率有可能下降到额定转速以内,使轴系产生共振,特别是螺旋桨轴径小于 250 mm 的具有人字架的船舶推进轴系,没有经过校中计算,如果现场施工校中不佳,运行中尾管前轴承脱空,使回转振动固有频率下降,导致共振转速进入或接近工作转速范围,从而出现严重的回旋振动[2]。

|
图 1 推进轴系布置图 Fig. 1 Layout of propulsion shafting |
某船为沿海航区的尾机型双体客船,具有人字架的推进轴系,螺旋桨(参数见表 2)选用 5 叶浆,主机(参数见表 1)输出经弹性联轴节、减速齿轮箱、中间轴、螺旋桨轴驱动定距螺旋桨,螺旋桨轴与螺旋桨以及螺旋桨与可拆联轴节采用键连接,轴系布置如图 1 所示,整个轴系设有尾管后轴承、尾管前轴承、中间轴轴承及齿轮箱大齿轮轴承等 4 道轴承作为支撑。
|
|
表 1 主机参数 Tab.1 Main engine parameters |
|
|
表 2 螺旋桨参数 Tab.2 Propeller parameters |
|
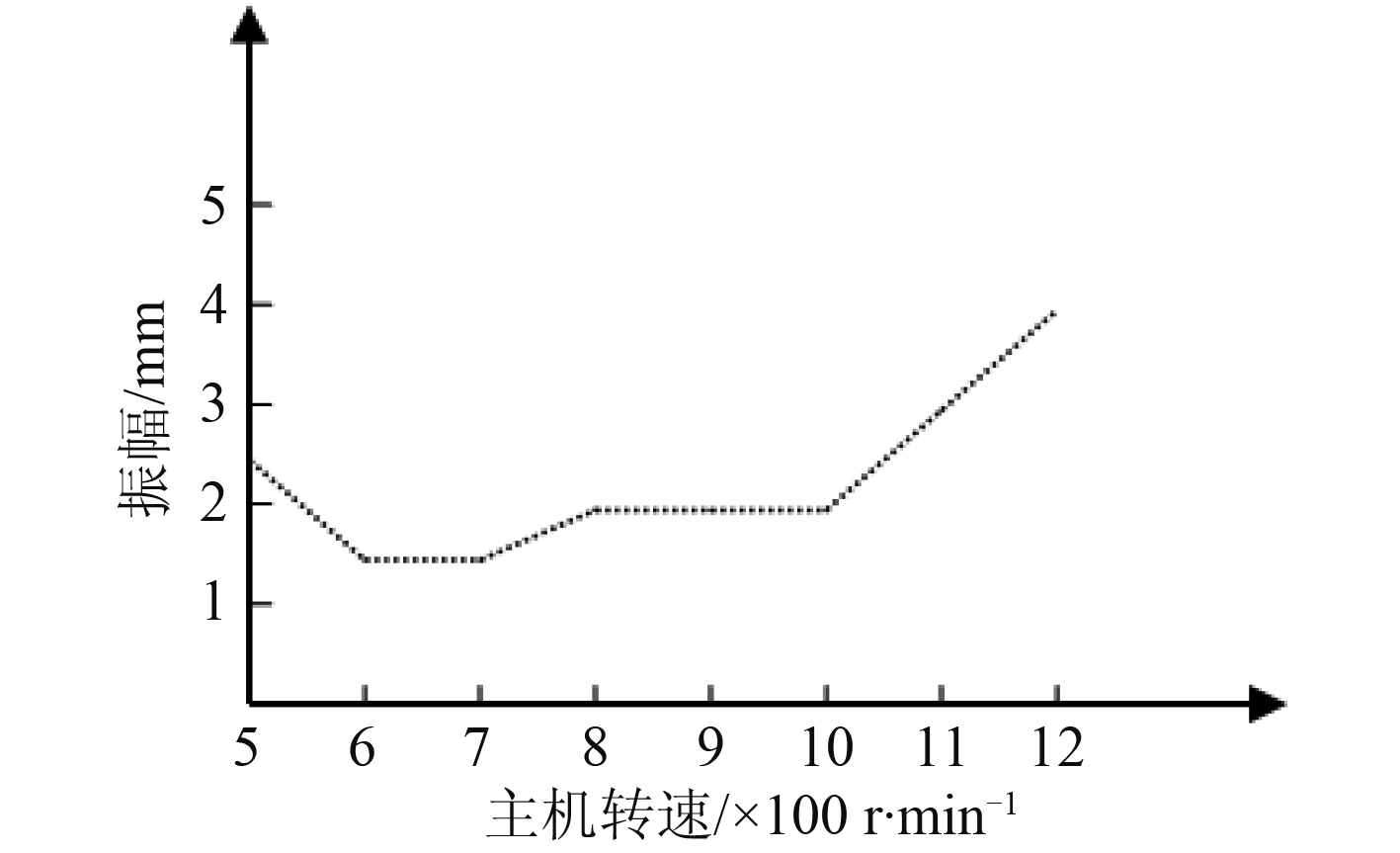
图 2 尾部甲板振幅与主机转速曲线图 Fig. 2 Stern deck vibration graph |
|
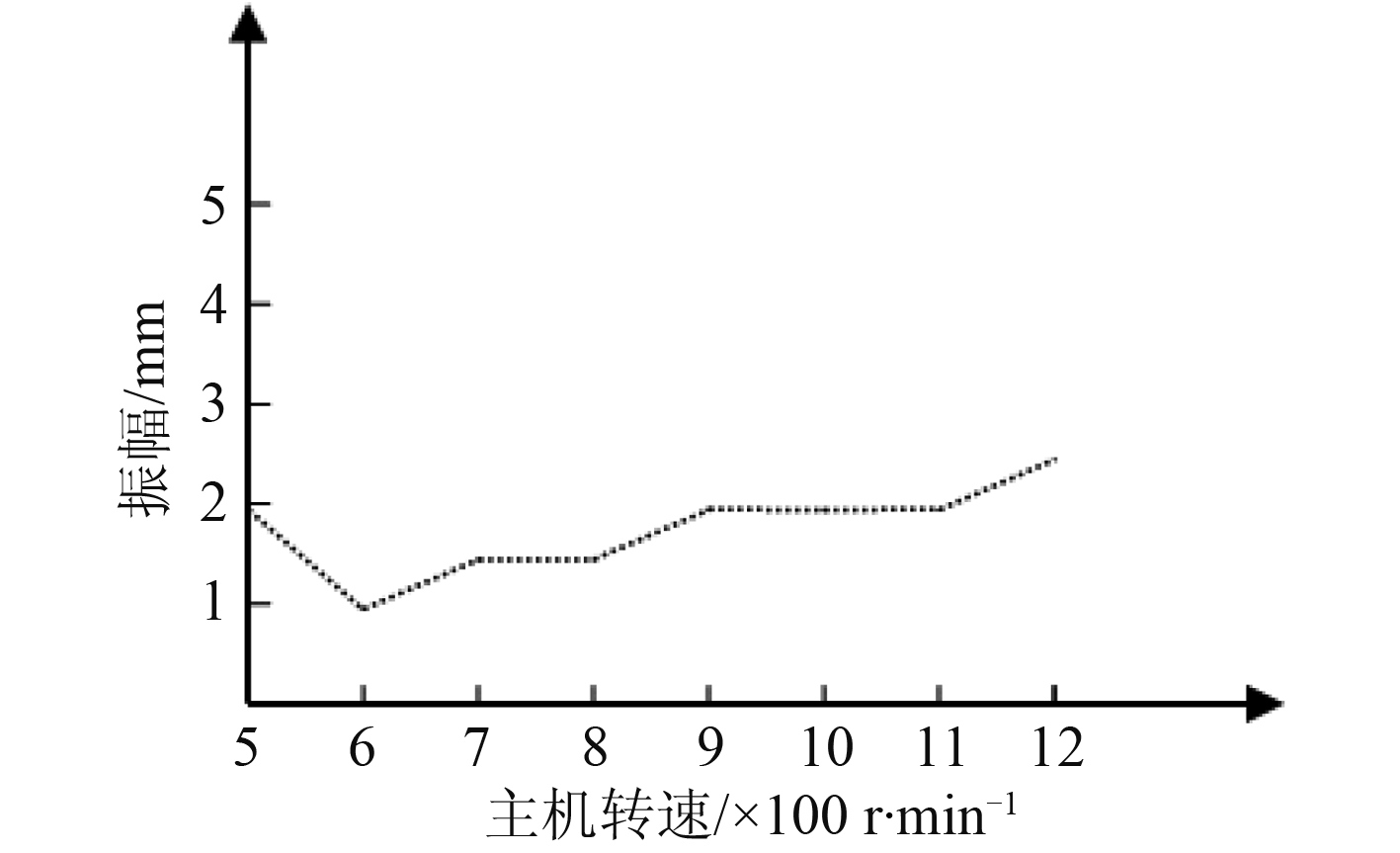
图 3 尾部甲板振幅与主机转速曲线图(整改后) Fig. 3 Stern deck vibration graph(rectification) |
该船在运营过程中,发现船体左片体尾部结构振动严重,严重影响了乘客的舒适性及尾部相关设备的寿命。通过对该船尾部甲板振动测量(见表 3)数据分析,当主机转速在 500 r/min 时,振幅较大,主要是主机及轴系在低速时与船体结构的小幅共振造成,该船最低稳定转速在 480 r/min,正常营运时,不会长时间在低速运行,所以不会对船舶造成影响。而当主机转速超过 1 000 r/min 后,振幅增大,船体尾部甲板振动剧烈,经初步分析,该船具有人字架的推进轴系,造成严重振动的原因应是回旋振动固有频率下降到额定转速范围以内,轴系与船体产生共振,从而导致轴承反力的动力放大,进而引起船体尾部结构的振动。
|
|
表 3 尾部甲板振动测量数据 Tab.3 Stern deck vibration data |
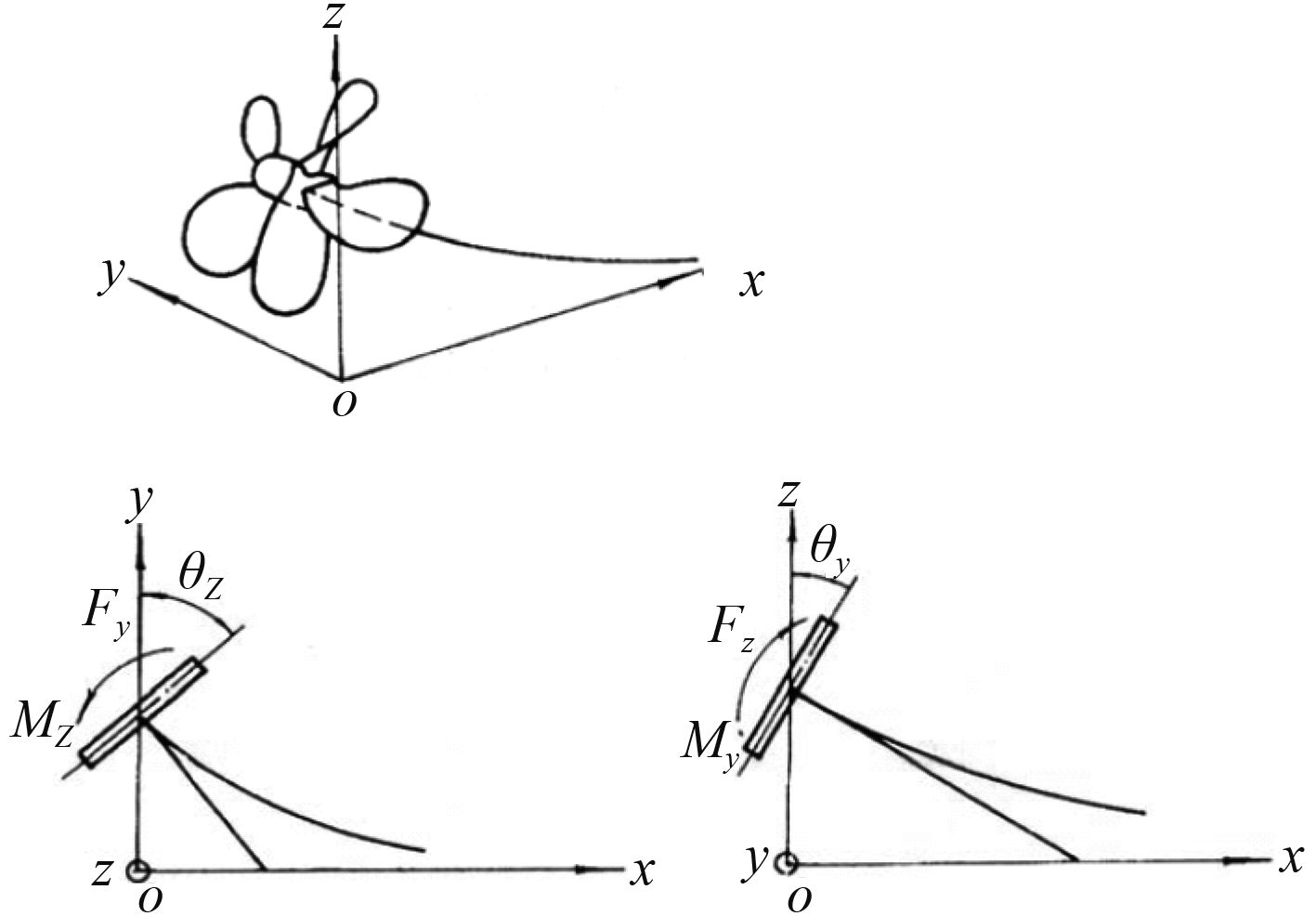
轴系的回旋振动用三维空间坐标系(x-y-z 坐标系)来描述,如图 4 所示。取螺旋桨中心的静平衡位置为坐标原点o,x 轴指向船首方向,y 轴指向水平左舷方向,z 轴垂直向上。推进轴系在水平、垂直平面上的投影如图 4 所示。轴线上任一点振动时的位移用y、z 坐标表示,螺旋桨平面的转角θy、θz 按右手定则取与坐标轴正向一致为正,作用在螺旋桨或轴系的力Fy 、Fz 与坐标轴的正向一致时为正,力矩(或弯矩)My 、Mz 按右手定则取与坐标轴的正向一致时为正[3]。
|
图 4 推进轴系在水平垂直平面的投影图 Fig. 4 Horizontal and vertical projection of shafting |
|
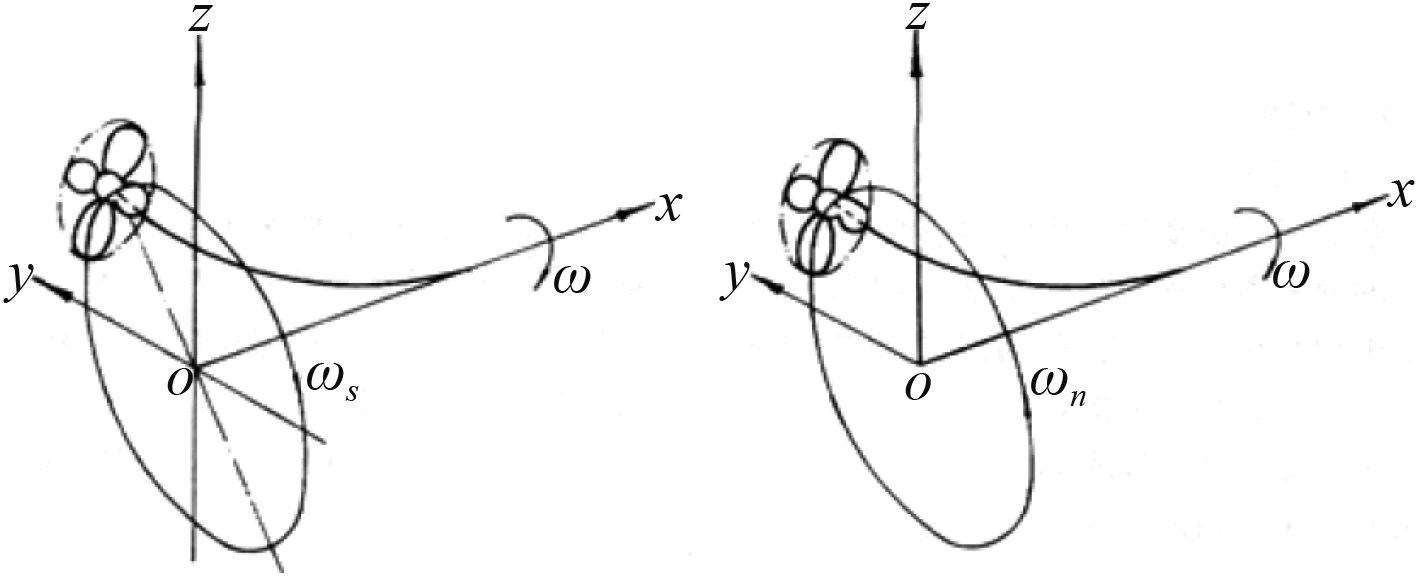
图 5 轴系正回旋与逆回旋 Fig. 5 Positive and inverse convolution |
推进轴系的回旋振动,是在悬臂端带有螺旋桨的多点支承转轴的进动运动。螺旋桨和转轴一方面以角速度ωs 绕其自身的几何轴线旋转,同时该轴线又以角速度ωn 绕ox 轴旋转。前一种旋转相当于自转,后一种旋转相当于公转。公转角速度ωn 又称进动角速度或回旋角速度。转轴上任一载面的绝对角速度ω 等于自转角速度ωs 与回旋角速度ωn 的矢量和,由于讨论的是微幅振动,则转轴上任一截面的绝对角速度可近似表示为:
| $\omega = {\omega _s} + {\omega _n}\text{。}$ | (1) |
当回旋角速度ωn 与自转角速度ωs 方向相同时,称为正回旋,反之,则称为逆回旋,如图 5 所示。
回旋振动模型将螺旋桨简化为一均质薄圆盘,其质量与转动惯量已包含附连水作用,转轴简化为一无质量弹性轴,忽略阻尼作用。回旋振动的频率方程为:
| $\left[ {\begin{array}{*{20}{c}}\!\!\!\!\!{1{\rm{ - m}}{\omega _n}^2{\delta _M}_z} \!\!\!\!\!& {{J_d}{\omega _n}^2{\delta _M}_z} \!\!\!\!\!\!\!&0 &\!\!\!\!\!\!\!\!\! {{J_p}\omega {\omega _n}{\delta _M}_z}\\\!\!\!\!\!\!\!\!\!{{\rm{m}}{\omega _n}^2{\Phi _{wy}}} & \!\!\!\!\!\!\!{{\rm{1 - }}{J_d}{\rm{ }}{\omega _n}^2{\Phi _{Mz}}} \!\!\!\!\!\!\!& 0 & \!\!\!\!\!\!\!\!\!{{\rm{ - }}{J_p}\omega {\omega _n}{\Phi _{Mz}}}\\\!\!\!\!\!0 & {{\rm{ - }}{J_p}\omega {\omega _n}{\delta _M}_z} & \!\!\!\!\!\!{{\rm{1 - }}m{\omega _n}^2{\delta _{Wz}}} &\!\!\!\!\!\! {{\rm{ - }}{J_p}{\omega _n}^2{\delta _M}_z}\\\!\!\!\!\!0 & {{\rm{ - }}{J_p}\omega {\omega _n}{\Phi _{Mz}}} & \!\!\!\!\!\!\!\!\!\!{{\rm{ - }}m{\omega _n}^2{\Phi _{Wz}}} &\!\!\!\!\!\!\!\!\!\!{{\rm{1 - }}{J_d}{\rm{ }}{\omega _n}^2{\Phi _{My}}}\!\!\!\!\!\!\!\!\end{array}} \right] = 0\text{,}$ | (2) |
式中:Jp、Jd 分别为螺旋桨的极转动惯量与径向转动惯量,kgm2;ω为螺旋桨的旋转角速度,rad/s;θz、θy为螺旋桨中心处轴在计算x-y 与x-z 平面的转角,rad;m为螺旋桨(包含附连水作用)质量,kg;δw 为螺旋桨处受到单位力作用时,其几何中心处产生的挠度,m/N;Φw 为螺旋桨处受到单位力作用时,其几何中心处产生的轴的转角,rad/N;δM 为螺旋桨处受到单位力矩作用时,其几何中心处产生的挠度,m/N;ΦM 为螺旋桨处受到单位力矩作用时,其几何中心处产生的轴的转角,rad/N;ωn 为回旋振动频率,rad/s。
当轴不旋转时,即ω = 0,式(2)就是轴系横向振动频率方程,由此求得的ωn 就是轴系横向振动固有频率。
采用传递矩阵进行轴系回旋振动计算,一般采用集总元件与分布参数元件相结合的简化模型,如图 4 所示,螺旋桨简化均质刚性圆盘元件,其质量与转动惯量作为集总参数,考虑附连水作用,螺旋桨轴、尾管轴、中间轴按自然分段为等截面均质轴段元件。为较清晰地绘制振型曲线,轴段元件可适当细分。一般可以忽略轴段回旋效应及剪力和轴向推力的影响,如法兰连接的弯曲刚度与轴相比要大得多,则可不考虑其弯曲变形,直接将两连接法兰作为均质刚性圆盘元件,轴段元件支撑刚度常用一等效弹簧处理,尾管后轴承刚度一般为 1 × 109~3 × 109 N/m,回旋振动计算分析中,将轴承简化为点支撑,对中间轴承、尾管前轴承,可以认为支反力沿轴向均匀分布,支撑点在轴承中点位置[4]。对尾管后轴承,由于悬臂端螺旋桨的作用,支撑反力沿轴承长度分布很不均匀,支撑反力合力的作用点偏向尾端,并受轴承磨损程度、船舶负载、船体变形等因素的影响。回旋振动计算时,对于白合金尾管后轴承,支点到轴承衬后端面的距离一般取轴承衬长度的 1/7~1/3[5]。
表4为该船主推进轴系主支数据,单元号 4、单元 8、单元号 19 和单元号 28 为轴承支点位置。
|
|
表 4 正常工况推进轴系主支数据 Tab.4 main propulsion shafting data of normal condition |
轴系尾端螺旋桨的边界为自由端,首端边界条件按其首端元件为飞轮、齿轮箱大齿轮或高弹联轴节分别取为固定端、铰支端或自由端。螺旋桨附水有质量和转动惯量 2 个作用,比较精确的值可用理论公式计算,初估时可用附加系数来表示:质量附水系数:1.10~1.30;极转动惯量附水系数:1.25~1.30;径转动惯量附水系数:1.50~2.0。在本计算中质量附水系统去 1.26,极转动惯量附水系数取 1.28,径转动惯量附水系数取 1.8。

|
图 6 正常工况回旋振动计算模型图 Fig. 6 Whirling vibration calculation model of normal condition |
根据上述图 1 可知,整个推进轴系包括艉管后轴承、艉管前轴承、中间轴轴承及齿轮箱大齿轮轴承等四道轴承作为支撑点,在计算模型中简化为弹簧支点,各个支撑点刚度数据见表 5 中所述,图 6 为通过 COMPASS 轴系计算软件建立的轴系回旋振动模型。
|
|
表 5 轴承参数 Tab.5 Bearing parameters |
经计算,叶片次正向回旋共振转速为 217.05 r/min,一次正回旋共振转速为 1 105.8 r/min,螺旋桨轴额定转速为 484 r/min,满足钢质海船入级规范要求,即叶片次正回旋共振转速不在螺旋桨轴额定转速的 0.85~1.0 范围内,1 次正回旋共振转速应不大于额定转速的 20% 以上[6],计算结果见表 6 所示,正常工况叶片次正向回旋振动弯矩、剪切力情况见图 7。
|
|
表 6 正常工况回旋振动计算结果 Tab.6 Normal condition whirling vibration calculation |
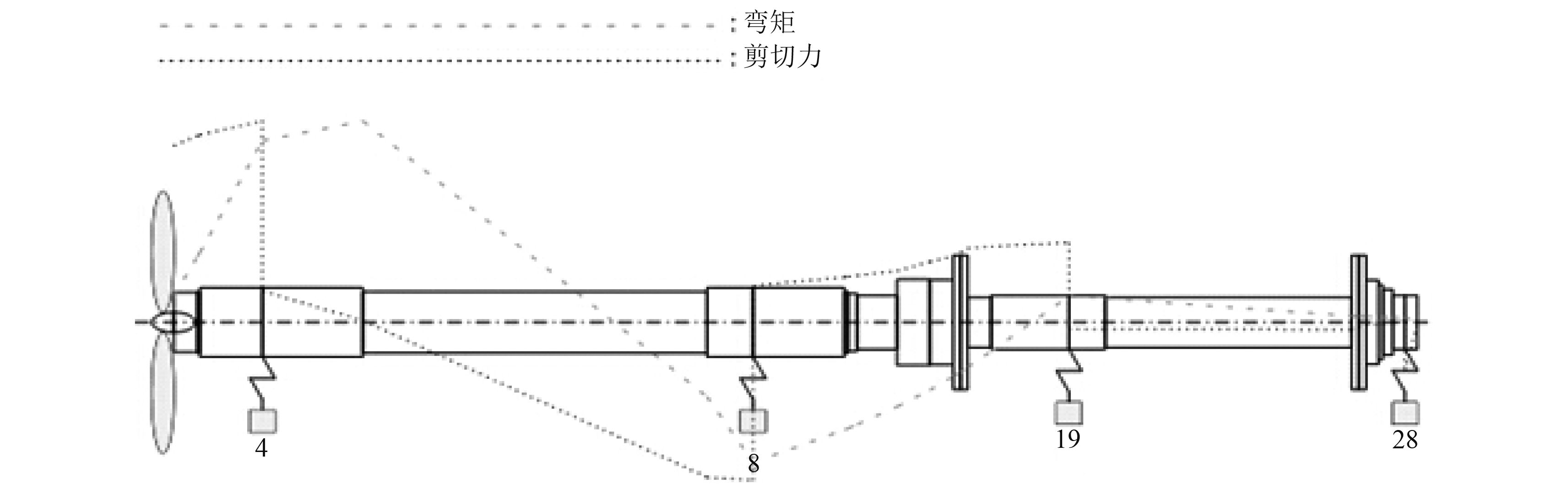
|
图 7 正常工况叶片次正向回旋振动弯矩、剪切力图 Fig. 7 Whirling vibration moment and shear of normal condition |
由于该船是螺旋桨轴径小于 250 mm,根据钢质海船入级规范的要求,推进轴系无需校中计算,现场施工才直接采用直线校中,如果现场施工校中不佳,运行中的过度磨损,会导致艉管前轴承及中间轴承脱空可能,现假设出现最恶劣工况,及尾管前轴承(单元号 8)和中间轴轴承(单元号 19)全部脱空,计算模型见图 8。

|
图 8 轴承脱空工况回旋振动计算模型 Fig. 8 Whirling vibration calculation model of bearing void condition |
根据上述计算发现,见表 7,当艉管前轴承和中间轴承脱空时,轴系固有频率大幅下降,轴系共振转速也下降,一次正回旋共振转速由 1 105.8 rad/min 下降为 475.2 rad/min,而螺旋桨轴额定转速为 484 rad/min,导致 1 次回旋振动固有频率下降到额定转速以内,使轴系产生共振,而严重的轴系回旋振动引起轴承反力的动力放大,进而引起船体尾部结构的振动,图 9 为推进轴系在艉管前轴承和中间轴承脱空工况下叶片次正向回旋振动弯矩、剪切力图,由图中可知当尾管前轴承和中间轴承脱空情况下,相对位移偏离较大,齿轮箱大齿轮端轴承(单元号 26)剪切力集中严重。
|
|
表 7 轴承脱空工况回旋振动计算结果 Tab.7 Whirling vibration calculation of bearing void condition |
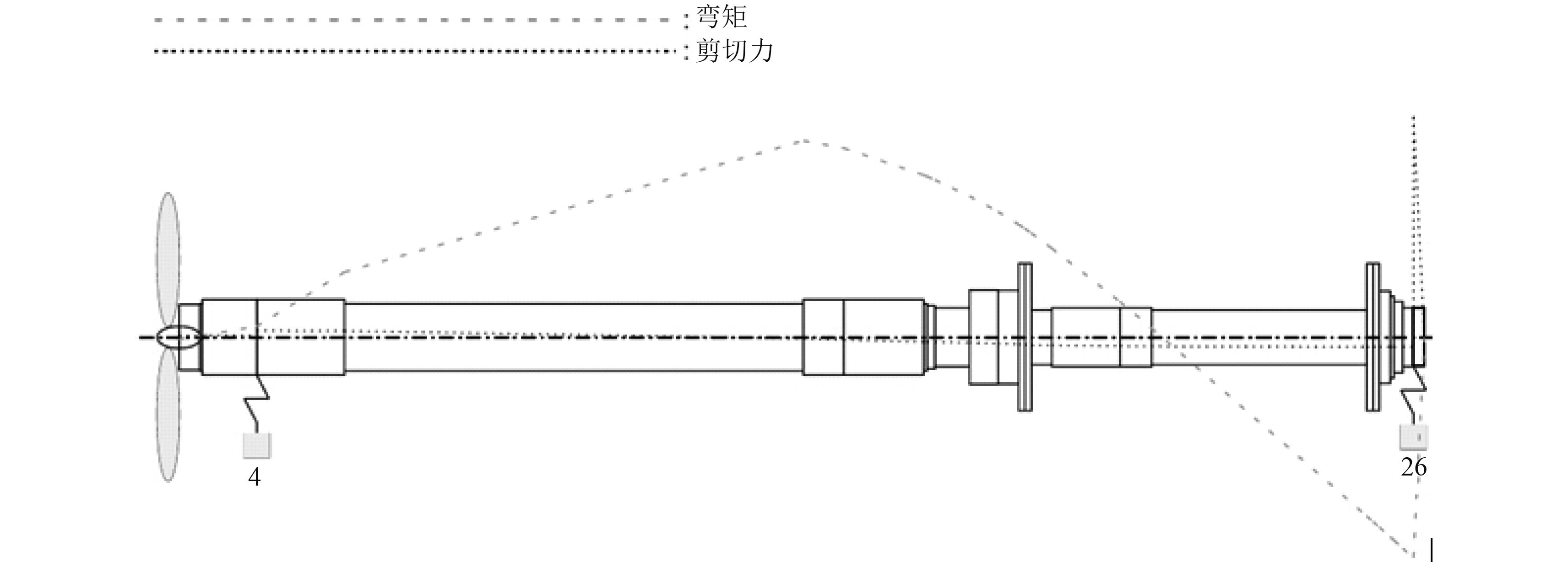
|
图 9 脱空工况叶片次正向回旋振动弯矩、剪切力图 Fig. 9 Whirling vibration moment and shear of bearing Void conditions |
经实船轴系检查,该船轴系由于校中不良,再加运行中的过度磨损,导致尾管前轴承脱空,轴系固有频率大幅下降,轴系共振转速也下降,由轴系回旋振动引起轴承反力的动力放大,进而引起船体尾部结构的振动。通过更换尾管前轴承,并适当调整中间轴承的位置,使轴系一次回旋共振转速大于螺旋桨轴的额定转速,解决了严重的轴系回旋振动导致的船体尾部结构振动,整改后重新对船体尾部振动进行测量,测量数据见表 3,通过图 2 与图 3 的曲线对比可知,通过更换尾管前轴承,并适当调整中间轴承的位置,当主机转速 1 000 r/min 以上时,尾部甲板最大振幅减小,解决了回旋振动引起的船体尾部结构振动问题。
4 结 语对于具有人字架的推进轴系,如果轴系校中不良,或船体局部变形导致轴承过度磨损脱空,轴承(特别是尾管前轴承)出现负的支反力,回旋振动的固有频率将大幅下降,可能使原先没有问题的回旋振动临界转速下降,落入工作转速范围内,出现严重回旋振动,引起轴承反力的动力放大,进而引起船体尾部结构的振动。因此对于具有人字架的推进轴系,为防止出现严重的回旋振动,在没有轴系校中计算的情况下,为防止轴承的可能脱空,应以最恶劣的工作对推进轴系的回旋振动进行计算,即如果推进轴系有尾管前轴承和中间轴轴承,在计算回旋振动时,假设其脱空,不把艉管前轴承和中间轴轴承当做弹性支点,如果在此种工况下计算所得回旋振动满足要求,则会大大降低推进轴系严重的回旋振动可能[7]。另外预防严重回旋振动的措施主要有:改变螺旋桨的叶片数,通常是减少叶片数,可改变叶片次临界转速,但这一措施不能调整 1 次临界转速;改变轴系直径,通常是加大螺旋桨轴直径,使刚度增加,同时又增大质量和转动惯量,最终效果是增大固有频率,避开正常转速范围;减少轴承间距,提高固有频率,但应防止轴系间距过小而引起轴承负荷分配不合理;另外应注意轴系校中应满足规范要求,以使轴系各轴承为正负荷,特别是艉管轴承和中间轴轴承,应在各种船舶工况下,均处于正负荷状态,从而避免船舶在运营过程中某个轴承的过度磨损[8]。
| [1] |
中国船级社. 船上振动控制指南[S]. 北京: 人民交通出版社, 2000: 102–115.
CCS. Guide for vibration control[S], Beijing: China Communications Press, 2000: 102–115. |
| [2] |
祁亮, 周瑞平, 崔金环. 中间轴承对船舶轴系回旋振动特性的影响[J]. 造船技术, 2011(04): 35-38, 45.
QI Liang, ZHOU Rui-ping, CUI Jin-huan. The effects of Intermediate bearing to whirling t vibration characteristics of ship shafting[J]. Marine Technology, 2011(04): 35-38, 45. |
| [3] |
陈锡恩, 高景. 船舶轴系回旋振动计算及其参数研究[J]. 船海工程, 2001(5): 8-11.
CHEN Xi-en, GAO Jing. Calculation and vibration parameters of whirling vibration of ship shafting[J]. Ship & Ocean Engineering, 2001(5): 8-11. |
| [4] |
夏极, 蔡耀全, 刘金林, 等. 轴承油膜动力特性系数对轴系回旋振动影响[J]. 舰船科学技术, 2016, 38(1): 62-66.
XIA Ji, CAI Yao-quan, LIU Jin-lin, et al. The influences of bearing hydrodynamic coefficients for whirling vibration of shafting[J]. Ship Science and Technology, 2016, 38(1): 62-66. |
| [5] |
张伟, 吴伟亮. 基于有限元法的气垫船轴系回旋振动特性计算[J]. 舰船科学技术, 2014, 36(10): 37-40.
ZHANG Wei, WU Wei-liang. The calculating of whirling vibration characteristics based on the finite element method[J] . Ship Science and Technology, 2014, 36(10): 37-40. |
| [6] |
中国船级社. 钢质海船入级规范[S]. 北京: 人民交通出版社, 2012: 1605–1606.
CCS. Rules for classification of sea-going steel ships[S]. Beijing: China Communications Press, 2012: 1605–1606. |
| [7] |
王建, 陈建伟, 闫方才, 等. 基于ANSYS的轴承磨损对船舶长轴系回旋振动的影响分析[J]. 交通科技, 2016(1): 167-170.
WANG Jian, CHEN Jian-wei, YAN Fang-cai, et al. The analysis of bearing wear to long shaft of ship maneuver system based on ANSYS[J]. Transportation Research, 2016(1): 167-170. |
| [8] |
张晓东. 尾轴承等效支点位置对轴系回旋振动的影响[J]. 船海工程, 2012(6): 53-56.
ZHANG Xiao-dong. The effects of Stern bearing equivalent fulcrum position to whirling vibration of shafting[J]. Ship & Ocean Engineering, 2012(6): 53-56. |
 2017, Vol. 39
2017, Vol. 39
