2. 船舶振动噪声重点实验室, 湖北 武汉 430033
2. National Key Laboratory on Ship Vibration, Wuhan 430033, China
多层材料吸声覆盖层对于潜艇的声隐身起着举足轻重的作用。多层材料吸声覆盖层是指敷设在潜艇表面具有吸声作用的一种功能性材料和结构,对于提高水下航行器的隐身性能作用显著,准确计算其声学性能具有重要意义[1, 2]。目前对含空腔的吸声覆盖层的研究主要有解析方法、数值方法等[3-5],这些研究大都在常压条件下进行,没有考虑外部静水压力的影响。因此在理论计算和有限元仿真中,所得到的结果与实际测试结果存在很大差别。实际使用的吸声覆盖层是在几百米深的水下工作的,其必然要受到静水压力的作用,声学效果也会随之发生改变。静压下吸声覆盖层吸声性能发生改变的原因主要有2个方面:一是材料的动态力学性能会随着压力而变化;二是吸声覆盖层受到静水压力时,空腔会发生形变。对于材料力学性能的研究,国内外许多学者针对类橡胶的粘弹性材料进行了很多测试和分析。随着有限元仿真软件在工程应用的普及,使用有限元对于解决声学计算问题是一种比较好的办法。姜闻文等[6]利用Ansys软件对几种橡胶结构的吸声覆盖层在静压下的吸声性能进行研究,比较了不同结构的空腔对吸声性能的影响;Panigrahi等[7]基于有限元法对不同组合空腔在静压下的声学性能进行了计算,并将结果与解析解、实验作了对比分析。
以上研究都是基于有限元法,首先计算静压下吸声覆盖层单元的几何变形,然后根据变形量重新建立吸声覆盖层的单元模型。由于空腔在静压下的变形是无规则、无规律可循的,即使得到静压下的变形量二次建模也很难与实际的空腔变形相吻合,这对后续的声学性能分析带来一定的误差。本文鉴于以上不足,利用COMSOL计算软件建立椭球形空腔的有限元模型,验证了模型的有效性并且分析在不同压力下和不同穿孔率下吸声覆盖层的声学性能。
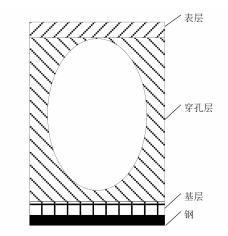
1 有限元模型 1.1 有限元物理模型的建立整个多层材料吸声覆盖层看成是由各个以椭球形空腔为中心的正六棱柱体组成,由于结构对称、重复,只需要研究其中一个棱柱体中的波传播即可。要建立一个六面棱柱体的理论模型比较困难。为了计算简便,本文通过用圆柱体近似代替六棱柱体,每个吸声覆盖层单元就可以简化为一段有限长粘弹性圆柱管。吸声覆盖层中波的传播与损耗问题可以模型化为粘弹性圆柱管中波的传播与损耗,这为建立理论模型提供了极大方便。如图 1所示为吸声覆盖层的一个单元。
|
图 1 吸声覆盖层一个单元 Fig. 1 A unit mode of anechoic coating |
考虑到吸声覆盖层单元具有轴对称性,因此在建模时将体单元模型(三维周期边界模型)简化为面单元模型(二维轴对称模型),材料参数如表 1所示。
|
|
表 1 吸声覆盖层结构和材料参数 Tab.1 The parameters of structure and material of anechoic coating |
圆柱形空腔的吸声覆盖层有限元模型比较成熟,陶猛[8]已多次验证了其有效性,但对椭球形空腔单元受压后直接计算其吸声性能的模型还没验证过其可行性。Gaunaurd[9]理论分析了受压前后椭球形空腔吸声覆盖层的穿孔率与静水压力的关系为:
| $ \varPhi (P)={{\varPhi }_{0}}{{e}^{-\frac{3p}{4\mu }}}\text{,} $ | (1) |
式中:μ为材料的剪切模量;P为静水压力;Ф为穿孔率。
本文正是利用式(1)穿孔率的理论模型与COMSOL有限元模型作对比,以验证模型的可行性。在如图 2所示的模型中,穿孔率可表示为:
| $ \varPhi (P)=\frac{{{V}_{c}}(P)}{{{V}_{v}}+{{V}_{c}}(P)}\text{。} $ | (2) |
式中Vc(P)和Vv分别为静压P下椭球形空腔的体积和橡胶基体的体积。
要证明模型的有效性,只要验证式(1)和式(2)中的Ф是否相同即可。但在静压P下Vc(P)是变化的,要想计算Vc(P),必须借助于高斯定理式(3)将曲面积分转化为曲线积分
| $ \int{(\nabla \text{ }\!\!\cdot\!\!\text{ }F){\rm d}V}=\oint{F\text{ }\!\!\cdot\!\!\text{ }{\rm d}}\text{。} $ | (3) |
在图示的二维轴对称模型中,主要是对空腔内表面进行曲线积分,
| $ \begin{aligned} & {A_{sphere}} \!=\!\! \int {1{\rm d}{A_{\rm sphere}}} \!=\!\! \int {\left( {\nabla \cdot \left[{\begin{array}{*{20}{l}} {amp;z}\\ {amp;0} \end{array}} \right]} \right){\rm d}{A_{\rm sphere}} = } \\ & \quad \quad \quad \int {( - z) \cdot {n_z}{\rm d}{l_{\rm sphere}}} \end{aligned} $ | (4) |
式中:Aspheroidicity为椭球形空腔的曲线积分;z为椭球形空腔内表面每一点的z向坐标;nz为z坐标的法向矢量;lspheroidicity为椭球形空腔的曲线。
得到空腔内表面的曲线积分后,再通过COMSOL中的“计算旋转几何的积分”选项就可以将求得的Aspheroidicity转化为椭球形空腔受压后的体积,即Vc(P)。对于橡胶基体体积Vv,在选用材料计算时,橡胶的泊松比在0.499左右,为几乎不可压缩材料,故Vv几乎不变。
在验证计算时,采用的橡胶材料的参数是随频率的改变而发生变化的,参数表达式根据实验数据拟合得到[10],橡胶材料的杨氏模量(单位:Pa)、损耗因子、泊松比表达式为:
| $ \begin{array}{l} E = 10 \times {10^6} - 0.1054{f^2} + 2272f\text{,}\\[6pt] \eta = - 8.21 \times {10^{ - 9}}{f^2} + 1.18 \times {10^{ - 4}}f + 0.204\text{,}\\[6pt] \sigma = 0.4992 - \frac{{0.01714}}{{1 + {{\left( {\frac{f}{{1044}}} \right)}^{2.65}}}}\text{。} \end{array} $ | (5) |
由于橡胶的杨氏模量为复杨氏模量,只要知道复杨氏模量的实部E和虚部η就可以求得复杨氏模量,故可表示为:
| $ \tilde{E}=E\times \left( 1+i\eta \right)\text{。} $ | (6) |
式中:f为频率,i为虚数。
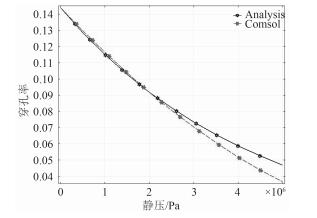
COMSOL有限元与解析公式通过计算得到的的结果如图 2所示。从图中可以看出,有限元与解析解的穿孔率变化曲线吻合程度较好。至于在静压较大的情况下有限元模型要比解析公式的穿孔率小,主要是由于解析公式在推导的过程中,假设计算单元中含有均匀分布的小气泡,总体积是压力函数,而COMSOL模型的初始穿孔率达到了16%,与解析公式中小气泡的假设存在一定的误差。
|
图 2 有限元与理论结果比较 Fig. 2 Comparison of FEM and theoretical results |
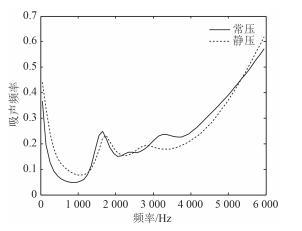
常压下多层料材吸声覆盖层的吸声性能与静水压力的情况下显著不同,如图 3所示,从图中可以看出,在静水压力下多层料材吸声覆盖层的低频吸声性能比常压下多层料材吸声覆盖层要好,静压下首个波峰时吸声系数是0.23对应的频率为1 750 Hz,常压下首个波峰时吸声系数是0.25对应的频率是1 700 Hz;在中高频的情况下,静压下多层料材吸声覆盖层与常压下吸声覆盖层吸声性能相差不大,在压力不同,吸声覆盖层的空腔结构受压变形也不一样,在工程应用时应该具体情况具体考虑。
|
图 3 常压下与静压下覆盖层吸声曲线的比较 Fig. 3 Contrast curves of sound coefficient between hydrostatic pressure and constant pressure |
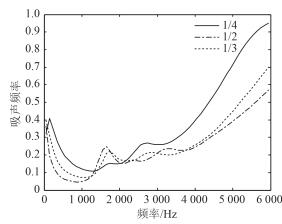
如图 4所示的是静水压力1 MPa下不同穿孔率下多层材料吸声覆盖层的吸声性能,穿孔率25%下的吸声覆盖层在低频和高频的表现比穿孔率33.3%和穿孔率50%的吸声覆盖层要好,其首个波峰的吸声系数是0.41其对应的频率为200 Hz;在中频表现方面3种穿孔率结构的吸声覆盖层吸声性能基本相同,从图中得出并不是穿孔率越大对于改善吸声覆盖层的低频吸声性能越好,只有在一定范围内的穿孔率能够解决吸声覆盖层低频吸声不好且保持中高频表现没有短板[11]。
|
图 4 不同穿孔率下吸声覆盖层的吸声性能 Fig. 4 sound coefficient of anechoic coating with different |
与目前静压下吸声覆盖层有限元研究不同,本文在利用COMSOL建模时,选用“固体力学”、“声-固耦合”、“移动网格”三大模块相结合,主要好处是单元模型在计算静压变形后,可以依靠“移动网格”直接将计算的变形应用于声固耦合计算中,不需要根据变形量二次建模,有效地提高了计算精度。如图6所示为1 MPa,3 MPa,5 MPa下的静压变形,吸声覆盖层的声学特性的计算在此变形基础上直接进行。从图中可以看出,吸声覆盖层随着压力的增大,椭球形空腔的形变量和覆盖层厚度的压缩量越大,且应力能越大。
椭球形空腔与圆柱形空腔虽然结构不同,但吸声系数走向不会发生太大的不同,趋势应该一致[12]。所以COMSOL计算结果与其他学者研究的结论存在差别的主要原因是:由于单元模型在静压下的变形呈不规则椭球形(见图 5),如若用计算的变形量重新建立模型,不可能与实际变形相对应;本文在计算声学特性时,单元采用的是受压变形后的实际模型,避免了以往根据变形量重新建模的误差,而这种不规则的形变造成了对声波吸收能力的减弱、对声波反射能力的增强,故计算的吸声系数总体下降。同时,从工程设计方面表明,若仅仅要求常压(即无静压作用)下设计的吸声覆盖层满足工程需要,那么在水下使用时会达不到想要的吸声效果,因为在水下不仅吸声频带发生变化,吸声性能也会明显的减弱。
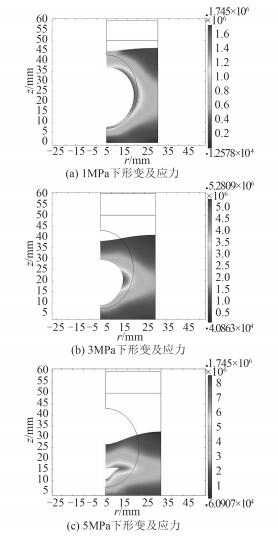
|
图 5 不同静压下单元形变及应力图 Fig. 5 Deformation and stress of unit under different hydrostatic pressure |
本文基于声波入射二维解析公式,利用COMSOL有限元软件建立静水压力下多层材料椭球形空腔模型,将计算的穿孔率与现有解析公式进行对比,验证了模型的有效性,然后计算了不同静压下模型单元的变形量,最后讨论了不同穿孔率对于吸声覆盖层的影响。结果表明:静压下多层材料吸声覆盖层的低频吸声性能比常压的要好,中高频方面两者相差不大;穿孔率25%下的吸声覆盖层在低频和高频的表现比穿孔率33.3%和穿孔率50%的吸声覆盖层要好,静压下穿孔率越大并不代表改善吸声覆盖层低频吸声性能越好;静压下吸声覆盖层随着压力的增大,椭球形空腔的形变量和覆盖层厚度的压缩量越大,且应力能越大。
| [1] |
孟晓宇, 肖国林, 陈虹. 国外潜艇声隐身技术现状与发展综述[J]. 舰船科学技术, 2011, 33 (11): 135–139.
MENG Xiao-yu, XIAO Guo-lin, CHEN Hong. Review of the present situation and development of acoustic stealth technology for submarines abroad[J]. Ship Science and Technology, 2011, 33 (11): 135–139. |
| [2] |
张浩, 傅欣艺, 尹铫, 等. 吸声覆盖层研究进展[J]. 应用声学, 2013, 32 (4): 295–304.
ZHANG Hao, FU Xin-yi, YIN Yao, et al. A review of anechoic coating research[J]. Applied Acoustics, 2013, 32 (4): 295–304. |
| [3] |
汤渭霖, 何世平, 范军. 含圆柱形空腔吸声覆盖层的二维理论[J]. 声学学报, 2005, 30 (4): 289–295.
TANG Wei-lin, HE Shi-ping, FAN Jun. Two-dimensional model for acoustic absorption of viscoelastic coating containing cylindrical holes[J]. Acta Acustica, 2005, 30 (4): 289–295. |
| [4] |
何世平, 汤渭霖, 何琳, 等. 变截面圆柱形空腔覆盖层吸声系数的二维近似解[J]. 船舶力学, 2006, 10 (1): 120–127.
HE Shi-ping, TANG Wei-lin, HE Lin, et al. Analysis of acoustic characteristics of anechoic coating containing varying sectional cylindrical cavity[J]. Journal of Ship Mechanics, 2006, 10 (1): 120–127. |
| [5] | EASWARAN V, MUNJAL M L. Analysis of reflection characteristics of a normal incidence plane wave on resonant sound absorbers:a finite element approach[J]. Journal of the Acoustical Society of America, 1993, 93 (3): 1308–1318. DOI: 10.1121/1.405416 |
| [6] | 姜闻文, 陈光冶, 朱彦. 静水压变化下橡胶结构吸声性能的计算与分析[J]. 噪声与振动控制, 2006, 26 (5): 55–57. |
| [7] | PANIGRAHI S N, JOG C S, MUNJAL M L. Multi-focus design of underwater noise control linings based on finite element analysis[J]. Applied Acoustics, 2008, 69 (12): 1141–1153. DOI: 10.1016/j.apacoust.2007.11.012 |
| [8] | 陶猛, 卓琳凯. 静水压力下吸声覆盖层的声学性能分析[J]. 上海交通大学学报, 2011, 45 (9): 1340–1344. |
| [9] | GAUNAURD G, CALLEN E, BARLOW J. Pressure effects on the dynamic effective properties of resonating perforated elastomers[J]. The Journal of the Acoustical Society of America, 1984, 76 (1): 173–177. DOI: 10.1121/1.391090 |
| [10] | 胡碰. 静水压力下声学覆盖层声学性能模块化方法研究[D]. 上海: 上海交通大学, 2008. |
| [11] | 姚熊亮, 刘文贺, 刘庆杰, 等. 水深与腔型对隔声去耦瓦吸声系数的影响[J]. 哈尔滨工程大学学报, 2007, 28 (6): 605–610. |
| [12] |
罗忠, 朱锡, 林志驼, 等. 水下吸声覆盖层结构及吸声机理研究进展[J]. 舰船科学技术, 2009, 31 (8): 23–30.
LUO Zhong, ZHU Xi, LIN Zhi-tuo, et al. A review of underwater anechoic coating structure and absorption theories[J]. Ship Science and Technology, 2009, 31 (8): 23–30. |
 2017, Vol. 39
2017, Vol. 39
