船舶动力定位是船舶依靠自身动力,在控制系统的作用下,抵抗外界干扰,使得船舶以某一首向到达设定的位置或者按照预定航迹运行。船舶在海面的运动是低频运动和高频运动的叠加,船舶的高频运动是一种往复运动,动力定位系统无需对其进行控制,因此,在进行动力定位时,需要将测量信息中的高频信息滤除,以获得船舶的低频信息。获得船舶准确的低频位置信息是船舶动力定位中的关键。动力定位船舶的状态观测器作为动力定位系统中分离船舶测量信息中的高频运动和低频运动的重要工具是动力定位系统研究的一大热点。
如今的动力定位船舶上大多用卡尔曼滤波的方法获得船舶低频信息,由于船舶是一个非线性系统,一般使用扩展卡尔曼滤波 EKF[1]和无迹卡尔曼滤波 UKF[2]来进行船舶低频状态预测,但是使用 EKF 在将非线性模型线性化的过程中忽略高阶项,很容易产生模型失配。使用 UKF 时,需要随着不同的噪声状况即时修改噪声协方差矩阵,否则就会出现滤波精度不佳的状况。由于粒子滤波[3 –4]的滤波过程对于噪声项不敏感,于是本文通过融合无迹卡尔曼滤波和粒子滤波设计了一种船舶状态估计算法,以提高同样参数设置下单独使用 UKF 算法的滤波精度。该融合算法的整体框图如图 1 所示。

|
图 1 融合算法整体框图 Fig. 1 Whole frame diagram of fusion algorithm |
对于通过算法从船舶运动的测量信息中分离出低频信息,首先就是要对船舶这个非线性系统以及其高频低频运动进行建模。
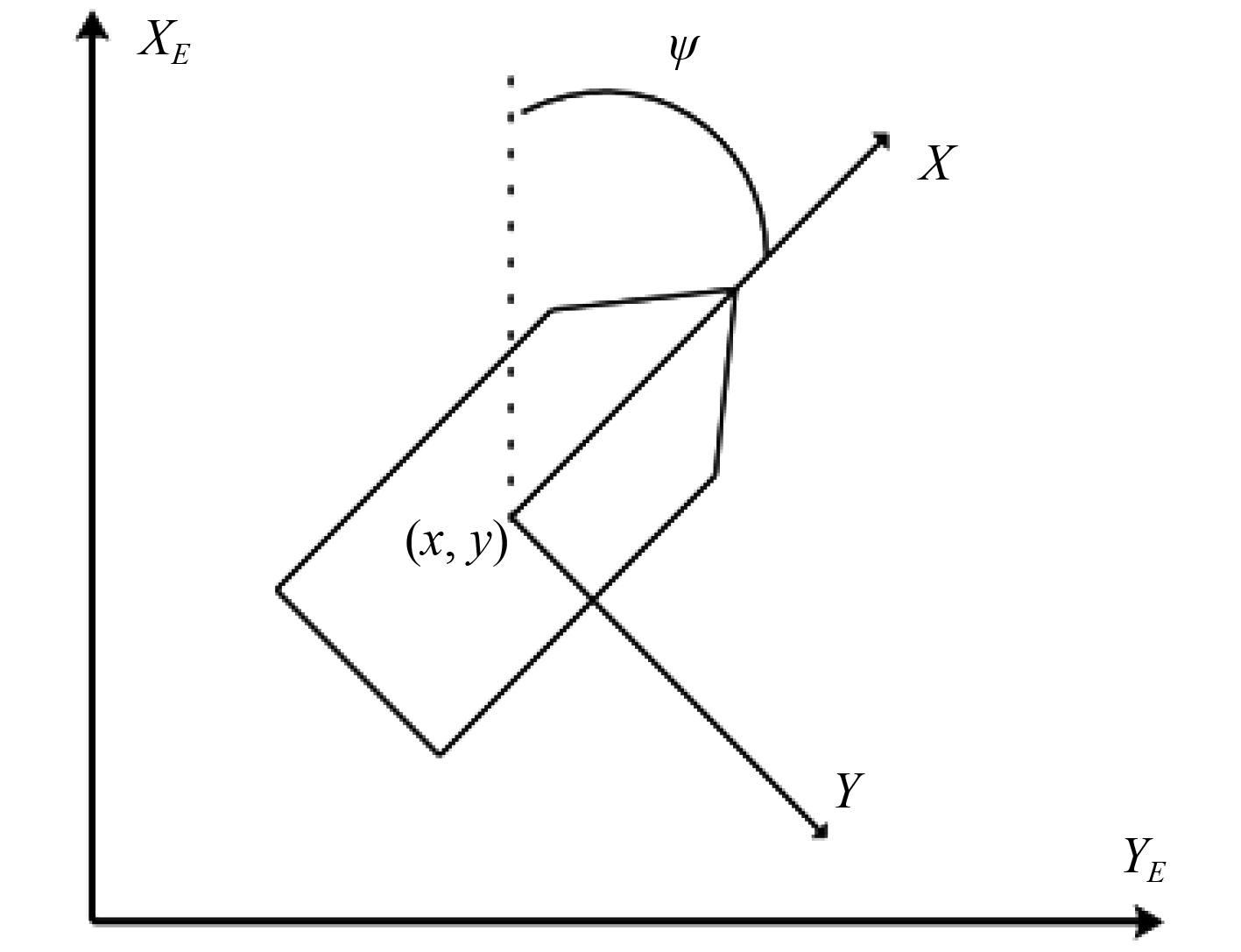
1.1 船舶的运动学模型动力定位控制的是船舶横荡、纵荡和首摇 3 个自由度的运动,为了描述船舶的运动一般建立地球坐标系O-XEYEZE 和随船坐标系O-XYZ,地球坐标系用来描述船舶的位置,随船坐标系用来描述船舶所受的水动力以及船舶的运动。由于随船坐标系不是一个惯性系,所以在运算的时候涉及到状态信息在这 2 个坐标系之间转换。地球坐标系和随船坐标系如图 2 所示。
|
图 2 地球坐标系与随船坐标系 Fig. 2 Earth coordinate system and ship coordinate system |
一般用
| $\dot \eta = R(\psi )v\text{,}$ | (1) |
其中,
| ${ R}(\psi ) = \left[ {\begin{array}{*{20}{c}}{\cos \psi } & { - \sin \psi } & 0\\{\sin \psi } & {\cos \psi } & 0\\0 & 0 & 1\end{array}} \right]\text{。}$ | (2) |
动力定位系统控制的船舶一般都是处于低速运动的情况下的,因此根据文献[5]可以得到简化的船舶低频运动模型:
| ${ M}\dot v + { D}v = \tau \text{。}$ | (3) |
式中: M 为船舶系统的惯量矩阵; D 为船舶的线性水动力矩阵; τ 为船舶所受的推进器推力和水动力的叠加;v 表示船舶的纵向速度、横向速度和首摇速度。
1.2.2 船舶的高频模型[5]仿真试验中一般使用二阶振荡器来模拟船舶 3 个自由度上的高频运动,转换成状态空间形为:
| $\left\{ \!\!\!{\begin{array}{*{20}{l}}{{{\dot \xi }_h} = {{ A}_h}{\xi _h} + {{ E}_h}{\omega _h}}\text{,}\\{{\eta _h} = {{ C}_h}{\xi _h}}\text{,}\end{array}} \right.$ | (4) |
式中:
| $\begin{aligned}{A_{21}} = & - {\rm diag}\{ \omega _{01}^2,\omega _{02}^2,\omega _{03}^2\} \text{,}\\[3pt]{A_{22}} = & - {\rm diag}\{ 2{\xi _1}{\omega _{01}},2{\xi _2}{\omega _{02}},2{\xi _3}{\omega _{03}}\} \text{,}\begin{array}{*{20}{c}}{}\end{array}\\[3pt]\Sigma = & {\rm diag}\{ {k_1},{k_2},{k_3}\} \text{。}\end{aligned}$ | (5) |
式中:ω0i 为谐振频率;ξi 为相对阻尼系数;k1,k2,k3 都为大于0的常数,表示白噪声的协方差。
由于本次的仿真主要来验证该算法跟踪效果,因此未加设定船舶所受外力为0,实际使用的船舶模型为:
| $\left\{ {\begin{array}{*{20}{l}}{{{\dot \xi }_h} = {{ A}_h}{\xi _h} + {E_h}{\omega _h}}\text{,}\\[6pt]{{\eta _h} = {{ C}_h}{\xi _h}}\text{,}\\[6pt]\!\!\!\! \begin{array}{l}{{\dot \xi }_l} = {{ A}_l}{\xi _l} + {E_l}{\omega _l}\text{,}\\[6pt]\!\! {y_l} = {{ C}_l}{\xi _l}\text{,}\\[6pt]\!\! {{ A}_l} = \left[ {\begin{array}{*{20}{c}}0 & {R(\psi )}\\[6pt]\!\! 0 & { - {M^{ - 1}}D}\end{array}} \right]\text{,}\\[6pt]{{ C}_l} = [0\begin{array}{*{20}{l}}{}\end{array}I]\text{,}\end{array}\\[6pt]{y = {y_l} + {\eta _h} + \nu }\text{。}\end{array}} \right.$ | (6) |
无迹卡尔曼滤波是 UT 变换和传统卡尔曼滤波的结合,其也是一种递推贝叶斯估计方法。无迹卡尔曼滤波是通过 UT 变换用一组确定的采样点来逼近系统的后验概率密度。对于非线性系统来说,通过这种方法可以略过系统线性化的环节,从而减少了线性化过程中的可能出现的模型失配问题。同时,对于高斯型的状态向量,采用无迹卡尔曼滤波无需计算雅各比矩阵和汉森矩阵,可以直接通过采样点得到状态向量的概率密度均值和协方差,相比于扩展卡尔曼滤波(EKF)有着很大的优越性。
2.2 粒子滤波粒子滤波是基于蒙特卡罗思想,其是通过在状态向量可能出现区域生成的若干随机粒子对系统的概率密度函数进行近似,以实际测量值和每个粒子的状态计算当前每个粒子的置信度,通过求均值的方法得到系统状态向量的估计值,从而得到状态向量的最小方差分布。由于其非参数化的特点,其对变量参数的非线性特性有着很强的建模能力,相比于 EKF 和 UKF,PF 的适用范围更广,精度也更高。
2.3 融合算法设计算法开始,首先在设定区域内对船舶所有可能出现的状态进行随机抽样,得到N 个粒子pi (i = 1,2,3…,N);根据各个粒子距离系统初始状态的远近计算每个粒子的初始的权值ωi (i = 1,2,3…,N)。
设K 时刻的第i 粒子相应的每个粒子的权值为ωi (k),将K 时刻的该粒子带入到船舶当前时刻的状态方程中,pi (k)得到K + 1 时刻该粒子状态的估计为:
| $\begin{array}{l}{p_i}(k + 1|k) = {A_l}{p_i}(k) + {E_l}{\omega _l}\text{,}\\[3pt]{y_{{p_i}}}(k + 1) = {C_l} \cdot {p_i}(k + 1|k) + {y_h} + v\text{,}\end{array}$ | (7) |
再对该粒子进行不敏变换,得到其 2n + 1 个σ 采样点:
| ${P}_k^i = [{p_i}(k) {p_i}(k) + \sqrt {(n + \lambda ){P_{k - 1}}} {p_i}(k) - \sqrt {(n + \lambda ){P_{k - 1}}} ] \text{,}$ | (8) |
对应的权值为:
| $W_k^i = [\lambda /(n + \lambda ) 1/2(n + \lambda ) 1/2(n + \lambda )]\text{,}$ | (9) |
其中,n 和λ 都为常数。
对粒子pi (k)进行 UKF 递推。
σ 采样点的一步预测:
| ${P}_{k + 1|k}^i = {A_l}{P}_k^i + {E_l}{\omega _l}$\text{,} | (10) |
粒子状态的估计:
| ${\bar p_i}(k + 1|k) = \sum\limits_{j = 1}^{2n + 1} {{W_{j,}}_k^i{{P}_{j,}}_k^i} \text{,}$ | (11) |
粒子状态误差协方差的一步预测:
| ${P_p} \!\!= \!\!\!{\sum\limits_{j = 1}^{2n + 1} {{W_{j,}}_k^i[{{P}_{j,}}_k^i \!-\! {{\bar p}_i}(k \!+\! 1|k)][{{P}_{j,}}_k^i \!-\! {{\bar p}_i}(k \!+\! 1|k)]} ^{\rm T}} \!\!+\! Q\text{,}$ | (12) |
σ 采样点测量的一步预测:
| ${Y_{{\rm P}_k^i}} = {C_l} \cdot {P}_k^i(k + 1|k) + {y_h} + v \text{,}$ | (13) |
粒子测量值的估计:
| ${\bar y_{{p_i}}}(k + 1|k) = \sum\limits_{j = 1}^{2n + 1} {{W_{j,}}_k^i} {Y_{j,{P}_k^i}}\text{,}$ | (14) |
粒子测量误差协方差的一步预测:
| ${P_y} \!\!=\!\!\! {\sum\limits_{j = 1}^{2n + 1} {{W_{j,}}_k^i[{Y_{j,}}_k^i \!- \!{{\bar y}_{{p_i}}}(k \!+\! 1|k)][{Y_{j,}}_k^i \!-\! {{\bar y}_{{p_i}}}(k \!+\! 1|k)]} ^{\rm T}} \!\!\!+\! R\text{,}$ | (15) |
粒子的量测和状态的互协方差为:
| ${P_{p,y}} = {\sum\limits_{j = 1}^{2n + 1} {{W_{j,}}_k^i[{Y_{j,}}_k^i - {{\bar y}_{{p_i}}}(k + 1|k)][{{P}_{j,}}_k^i - {{\bar p}_i}(k + 1|k)]} ^{\rm T}}\text{,}$ | (16) |
粒子状态的更新增益为:
| $K_k^i = {P_{p,y}}{P_y}^{ - 1}\text{,}$ | (17) |
第i 个粒子的状态和协方差的更新为:
| ${p_i}(k + 1) = {\bar p_i}(k + 1|k) + K_k^i({y_{{p_i}}}(k + 1) - {\bar y_{{p_i}}}(k + 1|k))\text{,}$ | (18) |
| ${P_{k + 1}} = {P_p} - K_k^i{P_y}K_k^{iT}\text{。}$ | (19) |
根据更新后的粒子状态以及当前时刻的实际的量测值来更新每个粒子的权值:
| ${\omega _i}\left( {k + 1} \right),\left( {i = 1,2,3, \ldots ,N} \right)\text{,}$ | (20) |
那么该时刻船舶的状态估计值为
| $x(k + 1) = \sum\limits_{i = 1}^N {{p_i}} (k + 1){\omega _i}(k + 1)\text{。}$ | (21) |
为了防止粒子退化,需要对粒子根据其归一化后的权值进行重采样,来淘汰权值比较小的粒子,复制权值大的粒子得到N 个新的粒子。
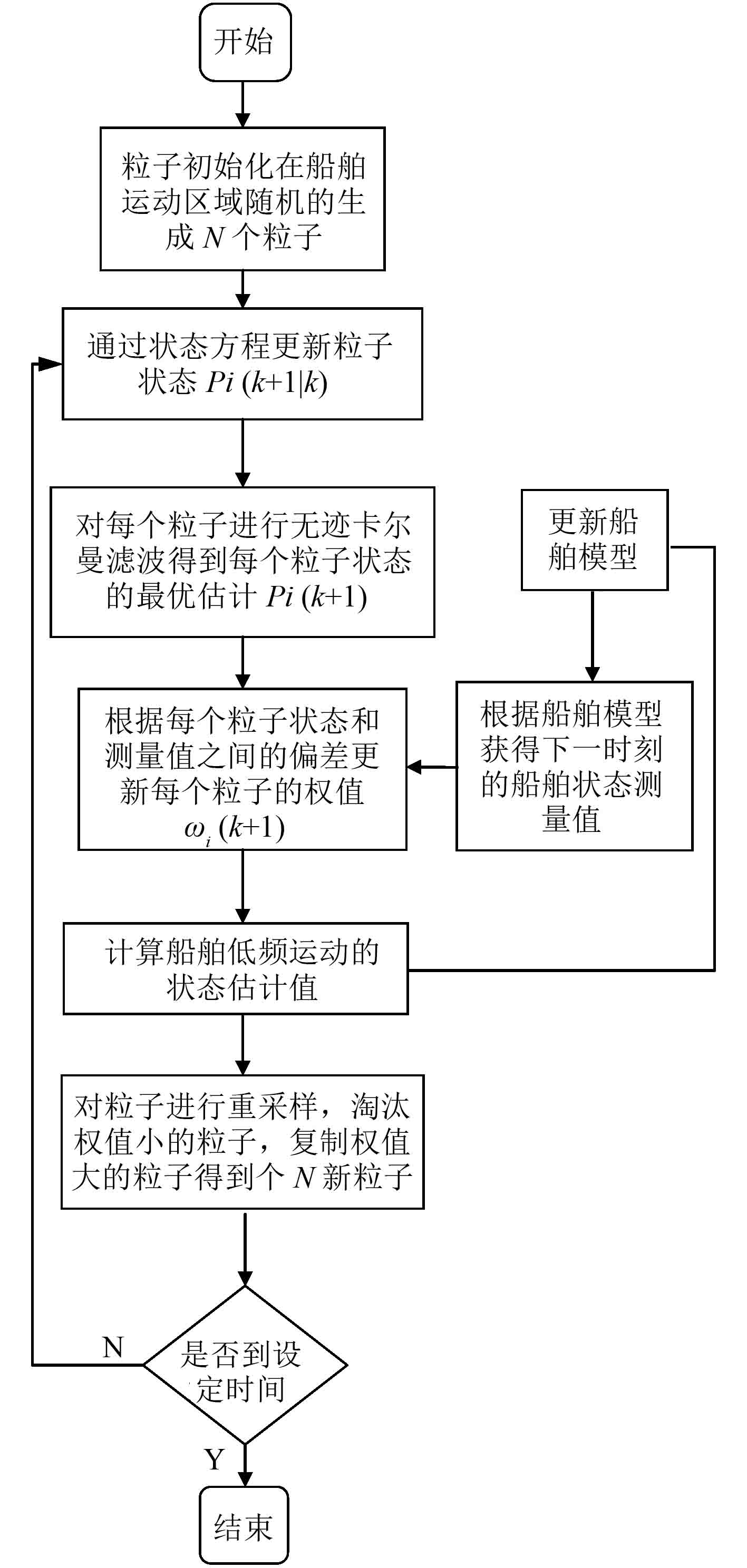
整个融合算法的框图如图 3 所示。
|
图 3 融合算法流程 Fig. 3 Fusion algorithm flow |
为验证算法的实用性,使用文献[5]中的船舶数据,其实船模型的主要参数如表 1 所示。
|
|
表 1 实船模型参数 Tab.1 parameters of the ship |
其无因次质量矩阵和阻尼矩阵分别为
| $\begin{array}{l}{ M} = \left[ {\begin{array}{*{20}{c}}{1.1274} & 0 & 0 \\0 & {1.8902} & { - 0.0744}\\0 & { - 0.0744} & {0.1278}\end{array}} \right],\\[20pt]{ D} = \left[ {\begin{array}{*{20}{c}}{0.0358} & 0 & 0\\0 & {0.1183} & { - 0.0124}\\0 & { - 0.0041} & {0.0308}\end{array}} \right]\text{。}\end{array}$ | (22) |
假设船舶的初始状态为
| $\left\{ \!\!\!\!{\begin{array}{*{20}{l}}{\xi = \left[ {\begin{array}{*{20}{c}}{0.06} & {0.1} & {0.15}\end{array}} \right]}\text{,}\\{{\omega _o} = 2\pi \left[ {\begin{array}{*{20}{c}}1 & {1/2} & {1/3}\end{array}} \right]}\text{,}\\{k = [\begin{array}{*{20}{c}}1 & {1.2} & {0.8}\end{array}]}\text{。}\end{array}} \right.$ | (23) |
选择粒子数N 为 100,采样时间为 1 s,仿真时间为 500 s 进行算法的仿真。
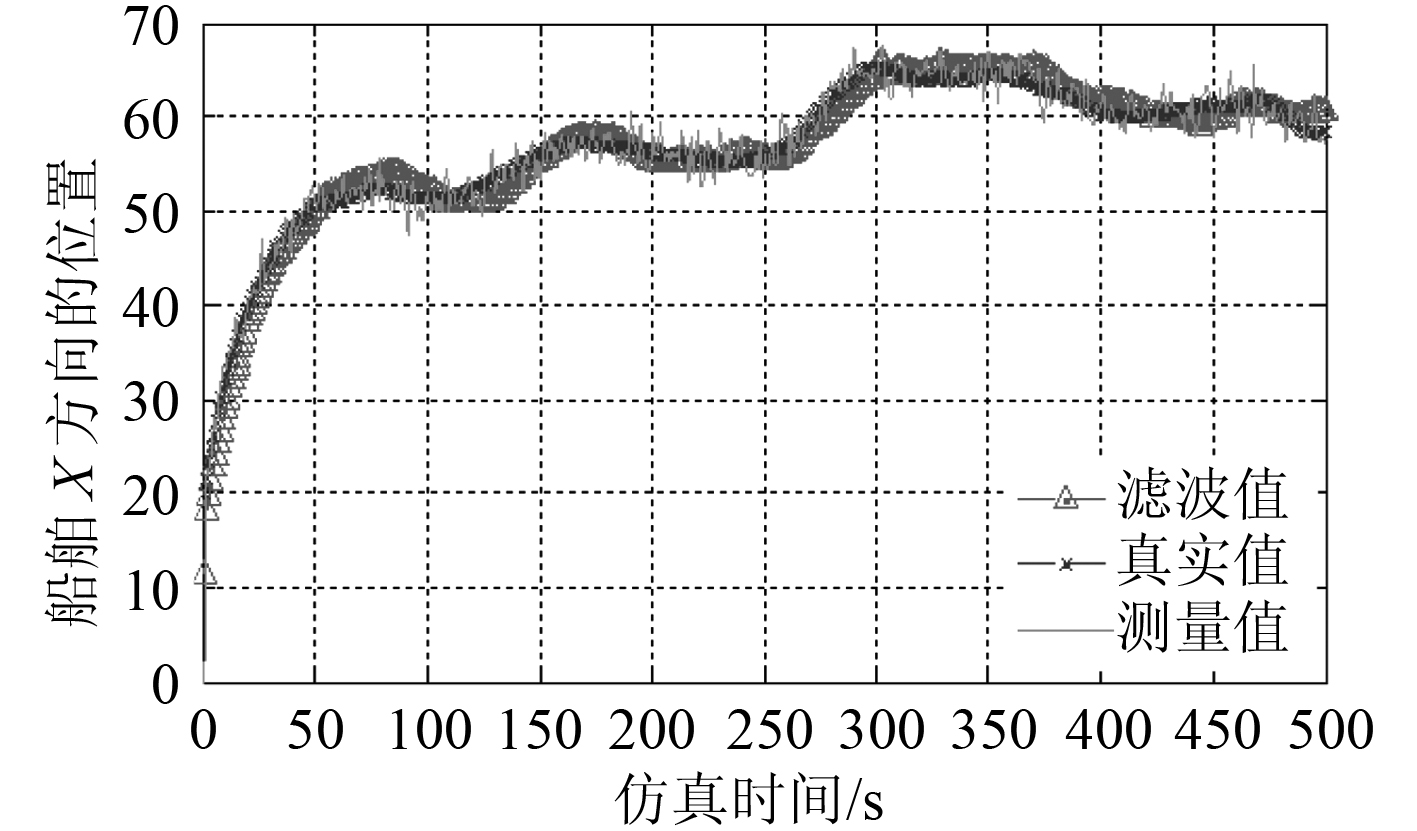
融合算法仿真结果如图4~图7所示。
|
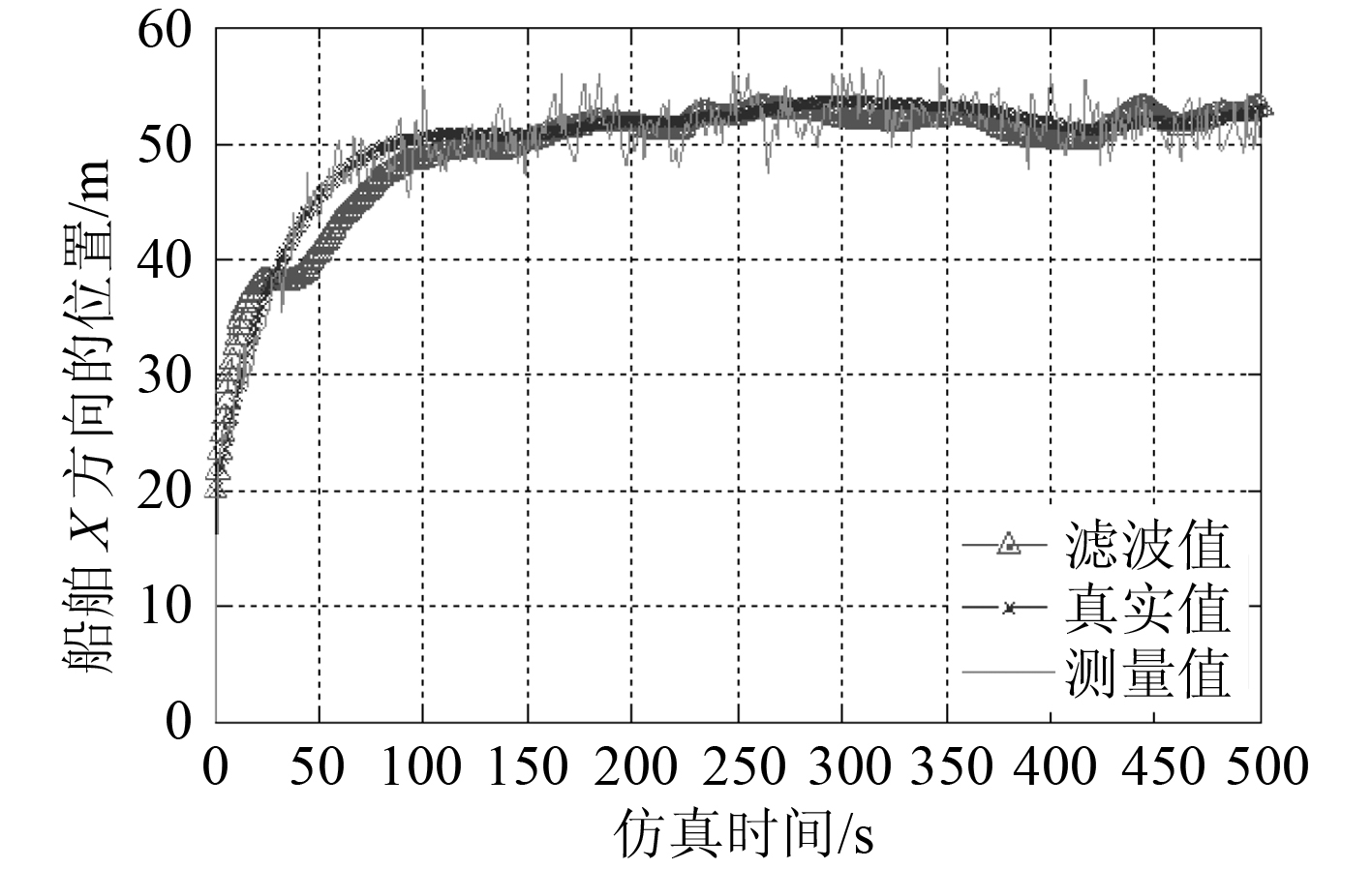
图 4 船舶X 方向的位置 Fig. 4 The position of ship in X axis |
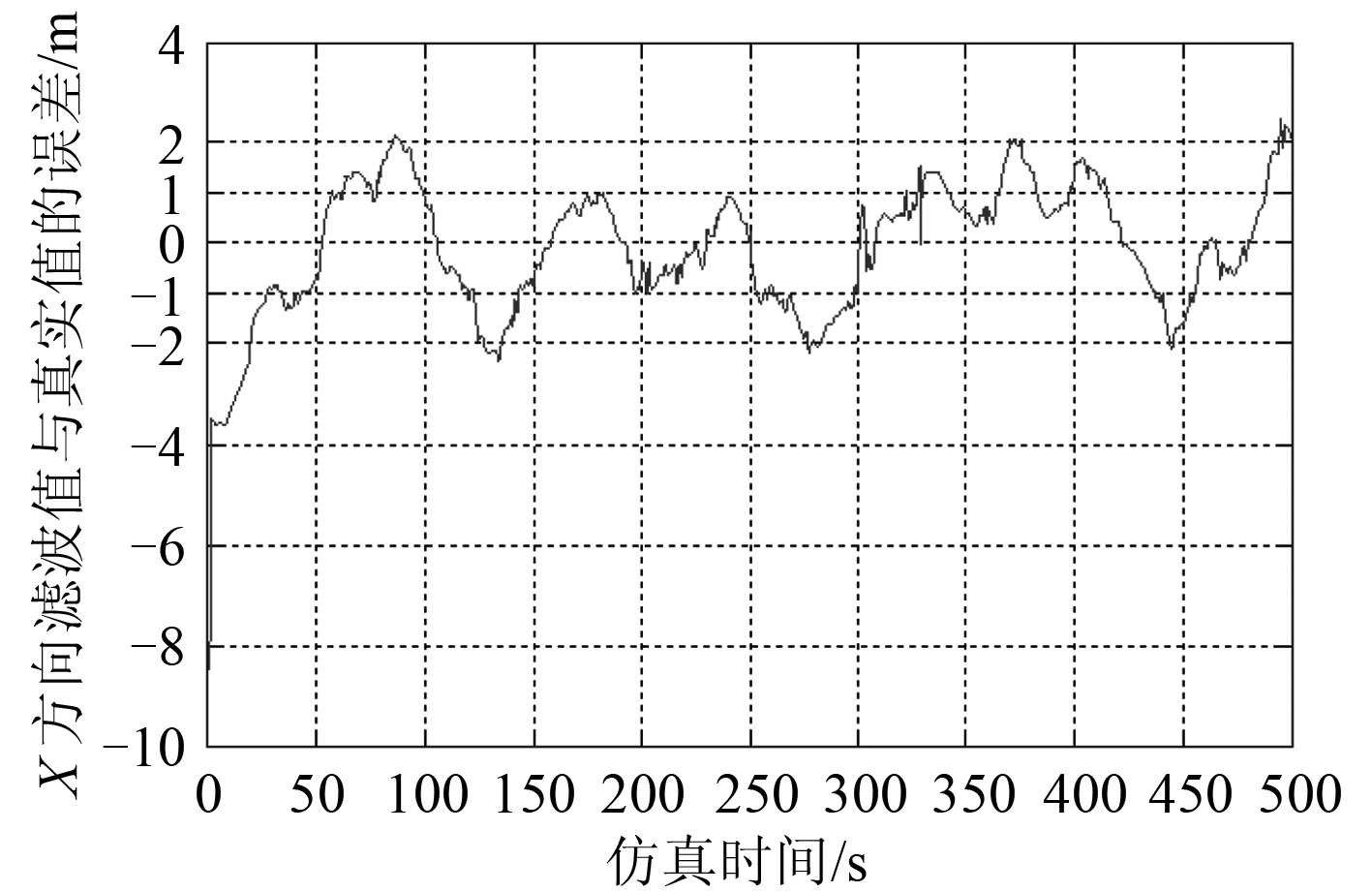
|
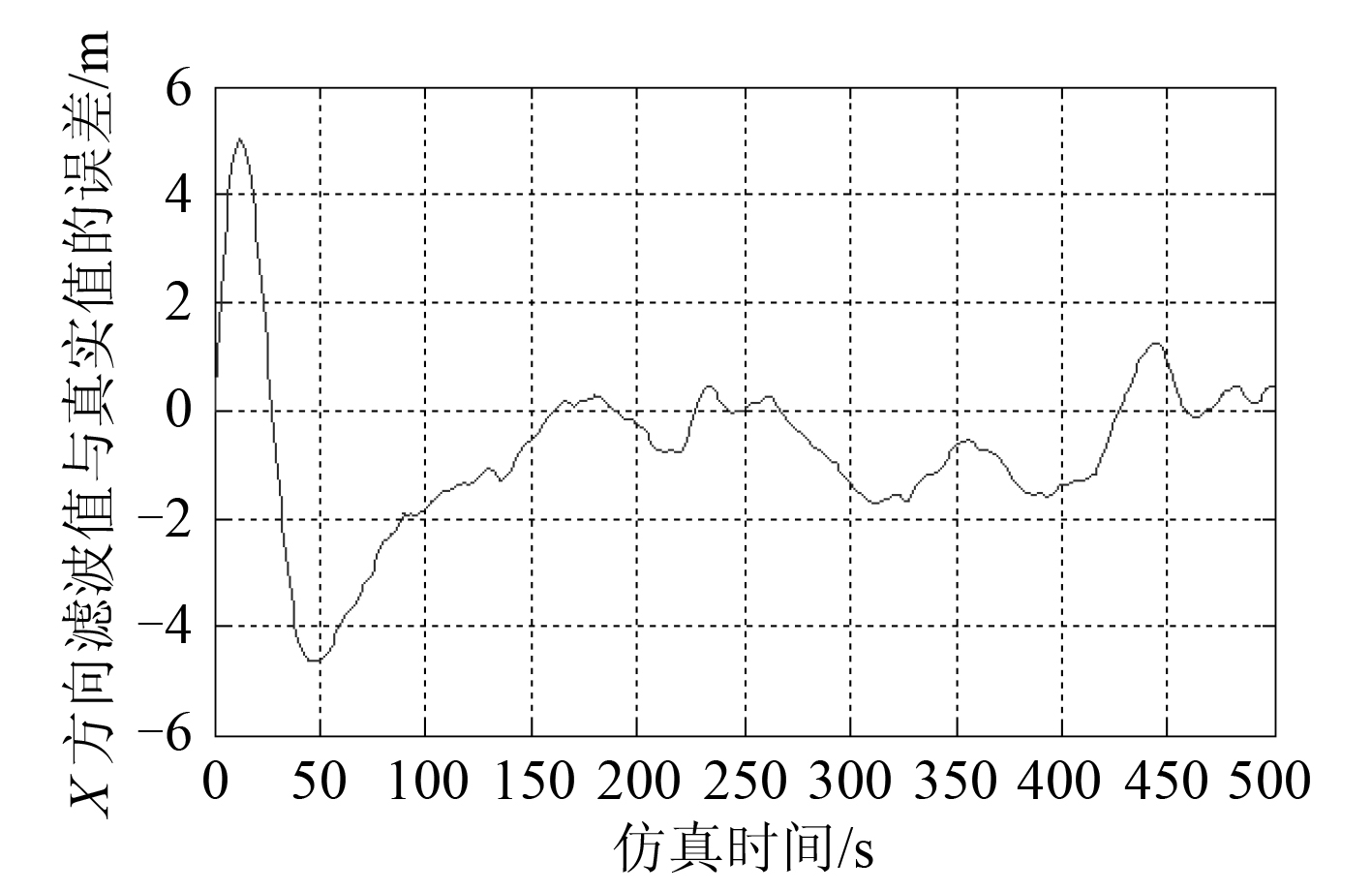
图 5 船舶X 方向位置滤波值与真实值的误差 Fig. 5 The error between estimated value and true value in X axis |
|
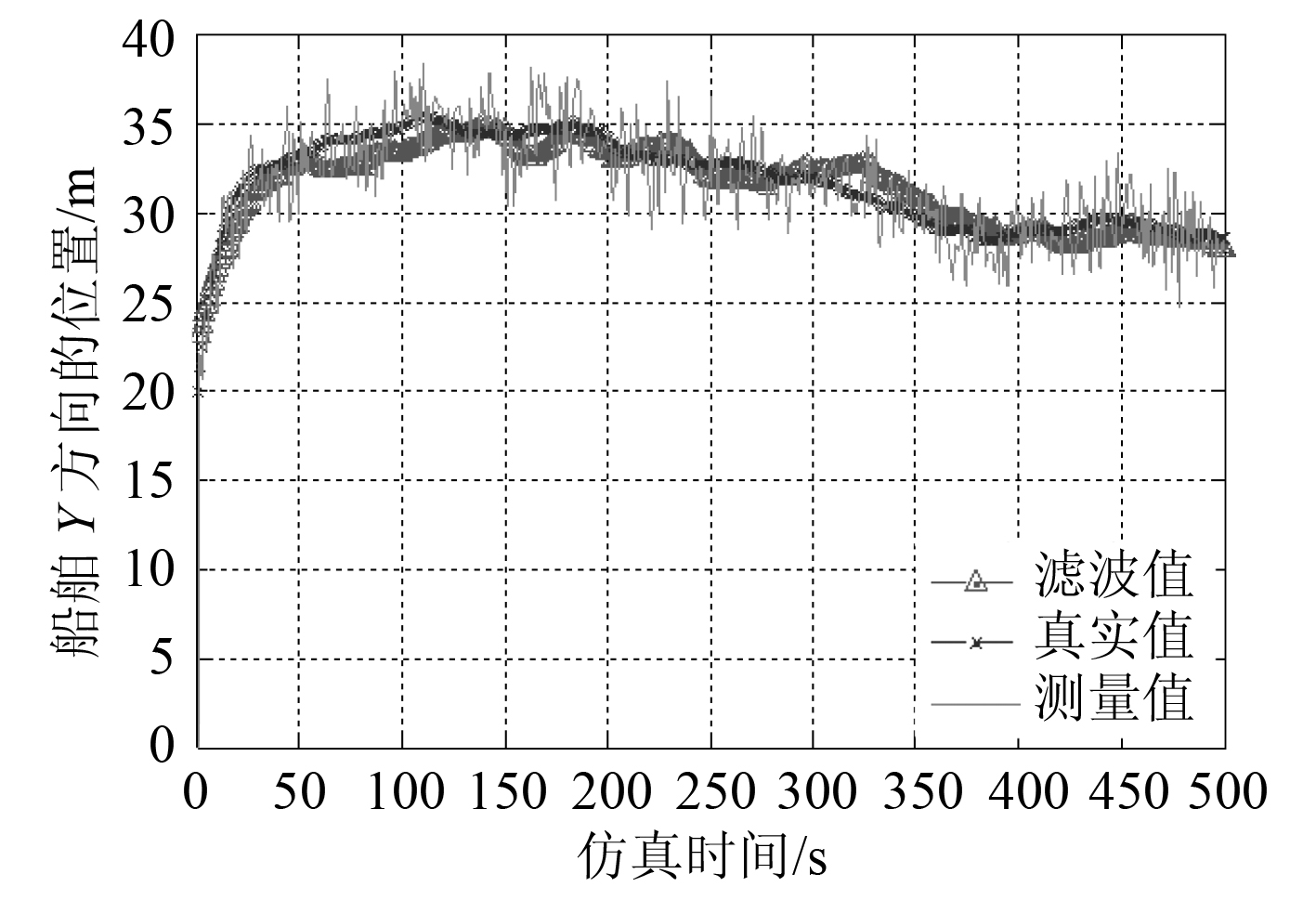
图 6 船舶Y 方向的位置 Fig. 6 The position of ship inY axis |
|
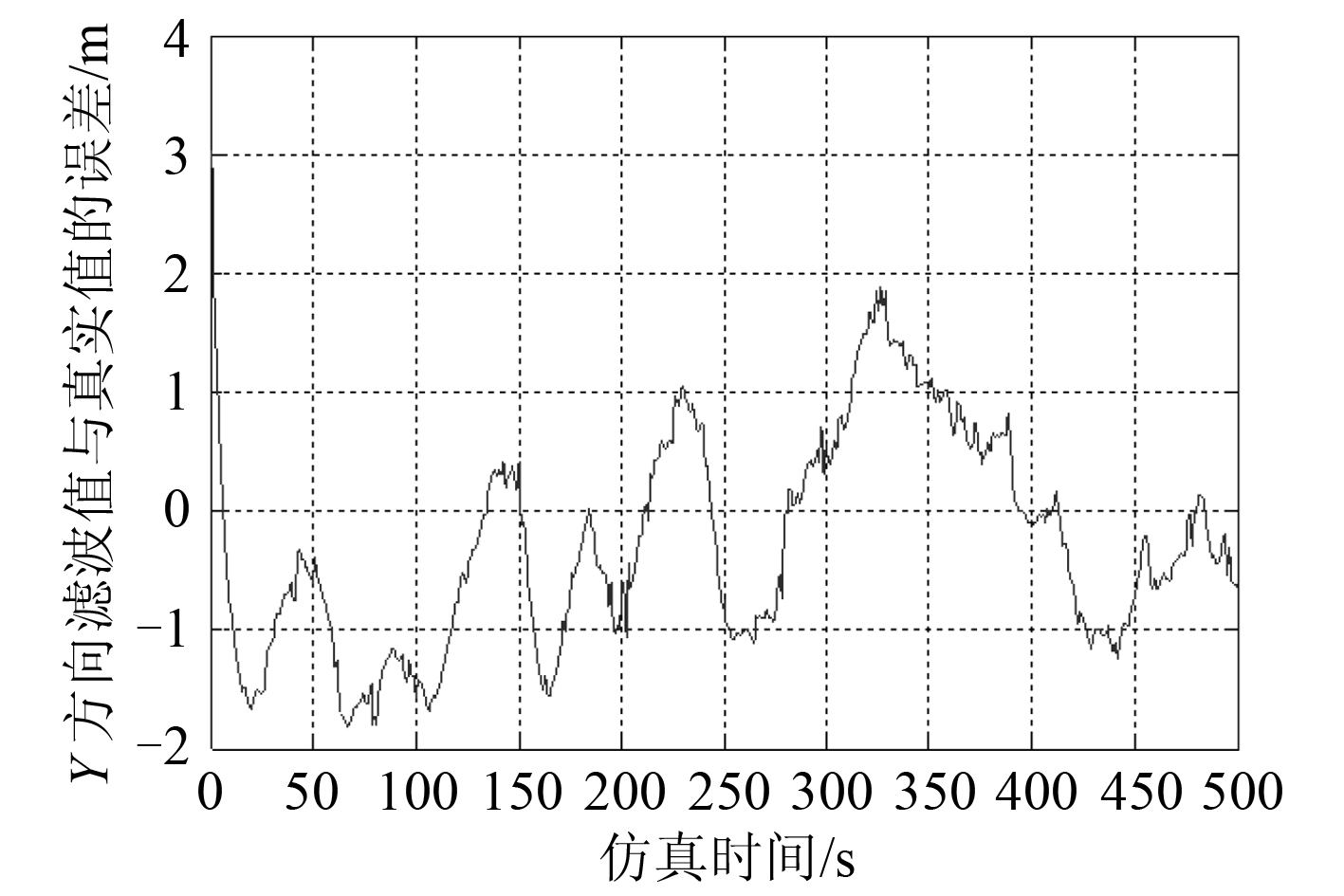
图 7 船舶Y 方向位置滤波值与真实值的误差 Fig. 7 The error between estimated value and true value inY axis |
|
图 8 船舶X 方向的位置 Fig. 8 The position of ship inX axis |
|
图 9 船舶X 方向位置滤波值与真实值的误差 Fig. 9 The error between estimated value and true value in X axis |
|
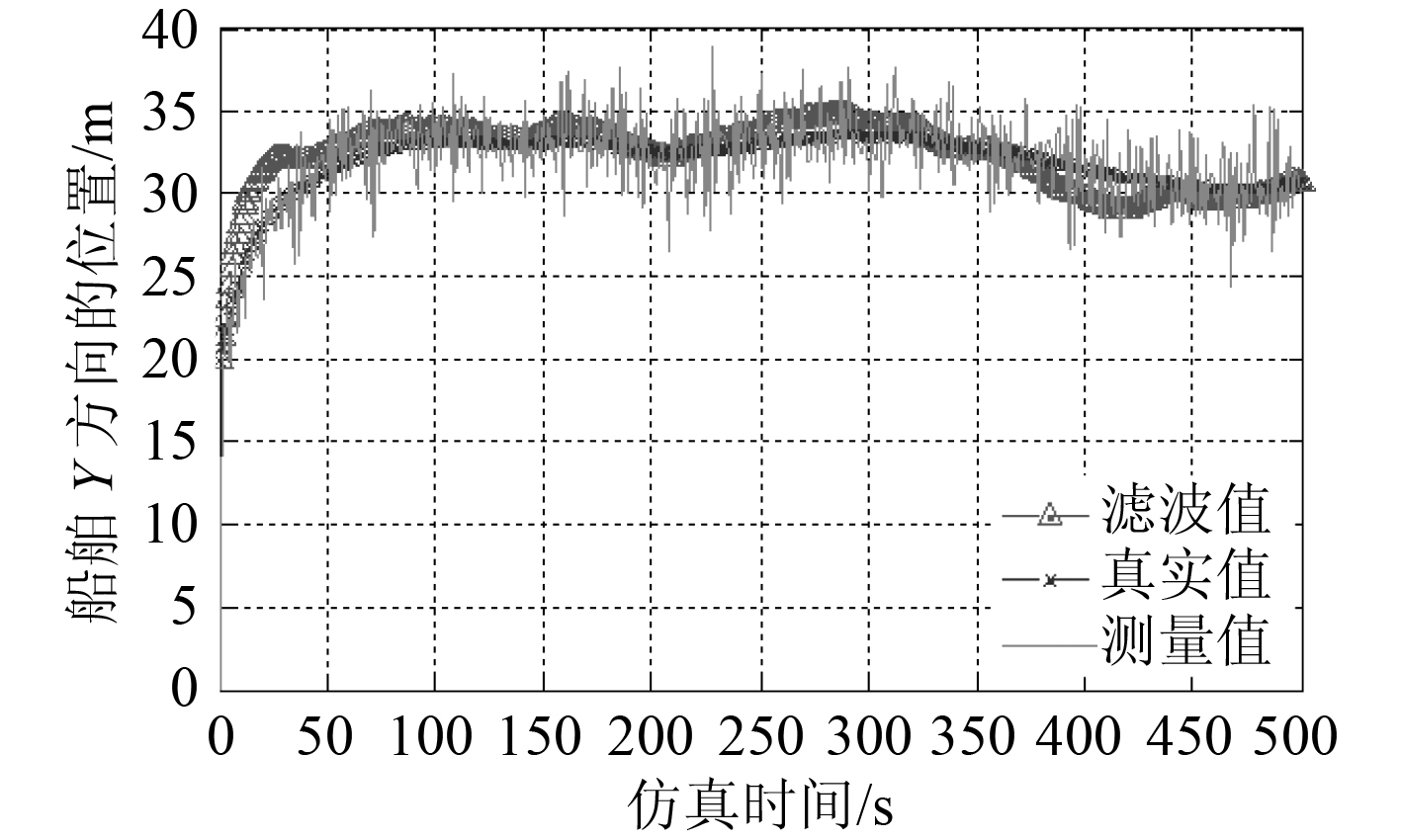
图 10 船舶Y 方向的位置 Fig. 10 The position of ship inY axis |
|
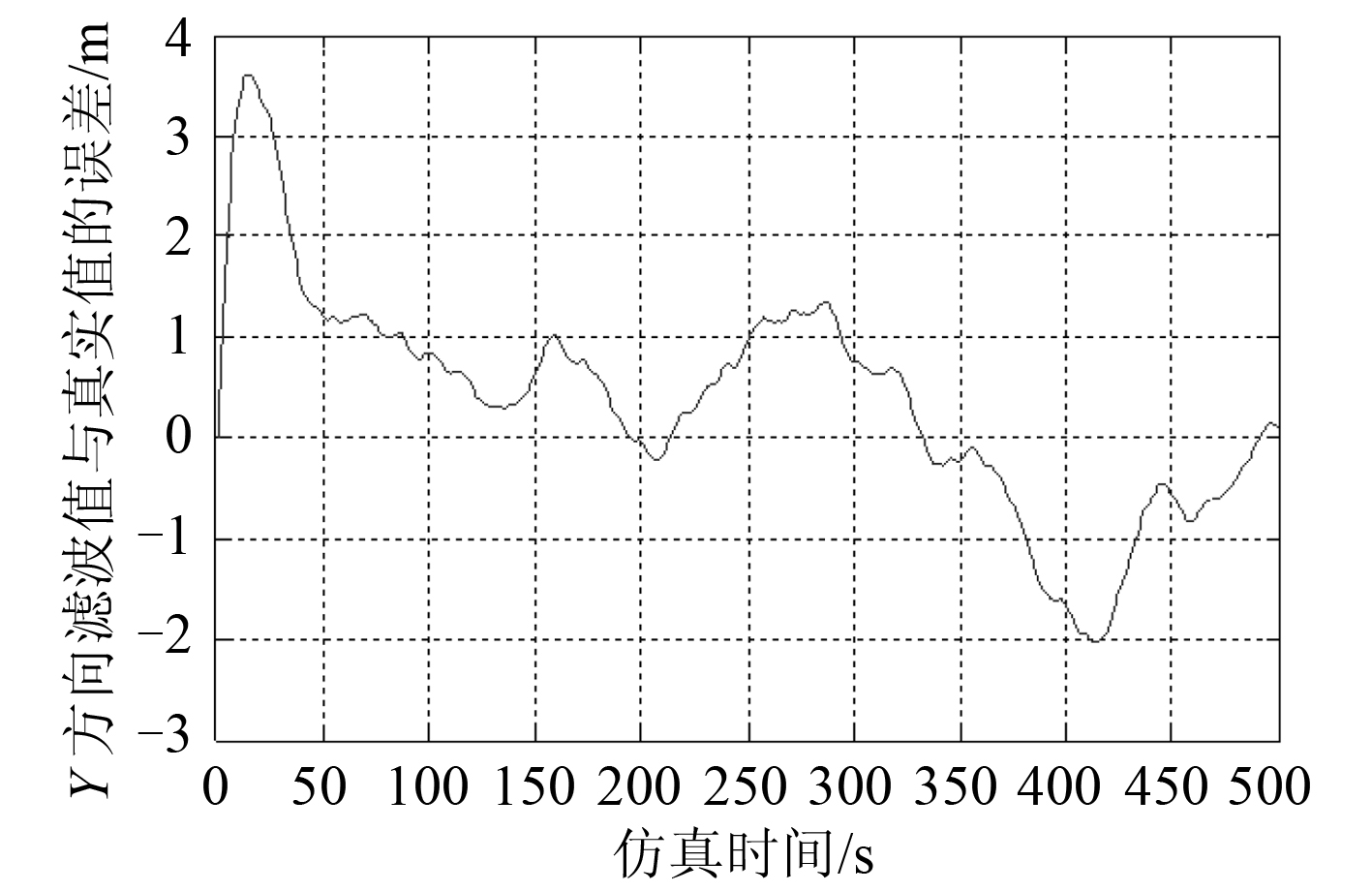
图 11 船舶Y 方向位置滤波值与真实值的误差 Fig. 11 The error between estimated value and true value inY axis |
仅用 UKF 算法的仿真结果如图 8~图 11 所示。
2 种算法的滤波效果对比如表 2 所示。对比 2 算法的滤波效果可知,融合算法在开始时由于粒子生成的随机性以及状态参数较多,在第 1 步估计时误差较大,但是随后就能立即减小误差,紧跟船舶的低频状态。而通过 UKF 得到的误差的在一个相对比较大的范围内震荡。从误差的均值和方差可以看出,在高频干扰和噪声同时存在以及 UKF 参数设置相同的条件下,融合算法的状态估计相比于只使用 UKF 精度更高,滤波的效果也比较稳定。
|
|
表 2 滤波效果对比 Tab.2 Filtering effect comparison |
船舶的状态估计在动力定位中有着极为重要的地位,对于船舶低频运动的估计的精度直接关系着动力定位系统的精度和稳定性。本文提出将粒子滤波与在船舶状态估计中使用广泛的 UKF 进行融合,得到一种融合算法。为了验证算法效果,本文将融合算法和仅用 UKF 算法进行了仿真对比试验。Matlab 仿真结果显示,该融合算法在滤波效果上总体优于单独使用 UKF 算法,滤波性能更加稳定。
| [1] | BALCHEN J G, JENSSEN N A, MATHISEN E, et al. A Dynamic positioning system based on Kalman filtering and optimal Control[J]. Modeling Identification & Control, 1980, 1(3): 135–163. |
| [2] | SHI X, SUN X, FU M, et al. An unscented Kalman filter based wave filtering algorithm for dynamic ship positioning[C]// Automation and Logistics (ICAL), 2011 IEEE International Conference on. IEEE, 2011:399–404. |
| [3] | DENG Xiao-long, JIN Jun, et al. A strong tracking particle filter for state estimation[C]// International Conference on Natural Computation, Icnc 2011, Shanghai, China, 26–28 July. 2011: 56–60. |
| [4] | WEI Q, XIONG Z, LI C, et al. A robust approach for multiple vehicles tracking using layered particle filter[J]. AEU - International Journal of Electronics and Communications, 2011, 65(7): 609–618. |
| [5] | 王元慧. 模型预测控制在动力定位系统中的应用[D]. 哈尔滨: 哈尔滨工程大学, 2006. |
 2017, Vol. 39
2017, Vol. 39
