由于在实际海洋环境中受波浪、风、海流等环境因素作用而不断产生各种摇荡运动,影响舰艇操纵和运动控制等任务执行。因此舰艇运动的计算分析,掌握外界干扰力带来的影响,对舰艇运动作业有重要意义。
海浪是引起海洋运动体摇荡的主要扰动,海浪是非常复杂的随机过程。本文基于不规则长峰波的计算基础上,开展波浪对舰艇干扰力的影响分析。结合频谱分析方法,探讨影响舰艇干扰力的主要因素,为舰艇在复杂海洋环境下的运动分析提供基础研究思路。
1 模型建立海浪对舰艇的干扰力的计算基于弗劳德-克雷洛夫假设定义,认为干扰力和力矩仅由流体压力引起;舰艇在流体中产生的压力场不会影响海浪的波场分布;海浪对海洋运动体的干扰力和力矩是水面下流体的压力场分布波动引起的[1 –2]。
在海洋运动体浸湿表面上每一点所受流体压力,等于海洋运动体的不存在,在其位置代之以虚拟的海洋运动体表面时,各点所受的流体压力。由于波浪中质点都在作轨圆运动,海洋运动体的存在实际上将干扰质点的正常运动代之虚拟表面后,水质点可以穿过这表面而不受阻碍,表面上各点压力可表示波浪压力计算,称为主干扰力。
针对舰艇的横荡运动情况,讨论横荡干扰力的计算方法[3 –4]。波面表达式为:
| ${\rm{\zeta }} = {{\rm{\zeta }}_{{a}}}{\rm{cos}}\left( {{{{k}}_1}{{x}} + {{{k}}_2}{{y}} - {{\rm{\omega }}_{{e}}}{{t}}} \right){\text{。}}$ | (1) |
不能忽略ζ 随y 的变化,因为只有ζ 随y 是变化的,才会产生横荡力,ζ 随y 的变化是横荡力根源,ζa 为波面的幅值,k 为波数,ω 为波浪的角频率,t 为时间。考虑舰艇的宽度B 较波长λ 小很多,认为波面在y 方向上的斜率是常数,推出舰艇引起的横荡力为:
| ${{Y}} = {\rm{\rho }g}{{{k}}_2}{{\rm{\zeta }}_{{a}}}\mathop \smallint \nolimits^ {{A}}\left( {{x}} \right)\sin \left( {{{{k}}_1}{\rm{x}} - {{\rm{\omega }}_{{e}}}{\rm{t}}} \right){\rm{d}}x{\text{,}}$ | (2) |
引入史密斯修正后的流体动压力作用下的横荡力:
| ${{Y}} \!\!=\!\! 2{\rm{\rho }}g{{\rm{\zeta }}_{{a}}}\mathop \smallint \nolimits^ {T}\left( {{x}} \right){{{e}}^{ - {{kT}}\left( {{x}} \right)/2}}{\rm{sin}}\left( {\frac{{{{{k}}_2}{{B}}\left( {{x}} \right)}}{2}} \right)\cos \left( {{{{k}}_1}{{x}} \!-\! {{\rm{\omega }}_{{e}}}{{t}}} \right){\rm{d}}x{\text{,}}$ | (3) |
针对横荡力对Z 轴求矩,沿x 轴积分,得出舰艇首摇干扰力矩为
| ${{N}} \!\!=\!\! 2{\rm{\rho }}g{{\rm{\zeta }}_{{a}}}\mathop \smallint \nolimits^ {{{e}}^{ - \frac{{{{kT}}\left( {{x}} \right)}}{2}}}\!\!{{T}}\left( {{x}} \right){\rm{sin}}\left( {\frac{{{{{k}}_2}{{B}}\left( {{x}} \right)}}{2}} \right)\cos \left( {{{{k}}_1}{\rm{x}} \!-\! {{\rm{\omega }}_{{e}}}{{t}}} \right){\rm{d}}x{\text{。}}\!\!\!$ | (4) |
海浪波形可分为规则波和不规则波。如果用规则波来仿真,不太切合实际波浪情况;故采用不规则波来模拟海浪波形,不规则波可以看作多种频率规则波的叠加。考虑到一般各种海浪频谱为狭带谱,用长峰波随机波对海浪仿真,选取某一频段的有限个数谐波,建立海浪信号的数学模型。
| ${\rm{\zeta }} = \mathop \sum \limits_{{\rm{i}} = 1}^{\rm{n}} {{\rm{\zeta }}_{{\rm{ai}}}}{\rm{cos}}\left( {{{{k}}_1}{\rm{cos\mu }} + {{{k}}_2}{\rm{sin\mu }} - {{\rm{\omega }}_{\rm{e}}}{{t}} + {{\rm{\varepsilon }}_{\rm{i}}}} \right){\text{。}}$ | (5) |
式中:μ 为遭遇角;εi 为初相位。
采用波能谱(海浪谱)描述海浪的统计特性,最终利用海浪反演的线性叠加法模拟出不规则长峰波海浪。
2 仿真分析选取某船长L=125 m;船最大宽 20 m;平均吃水 6.5 m;船速 9.2 m/s。计算横荡力和首摇力矩,其中横荡力Y 用
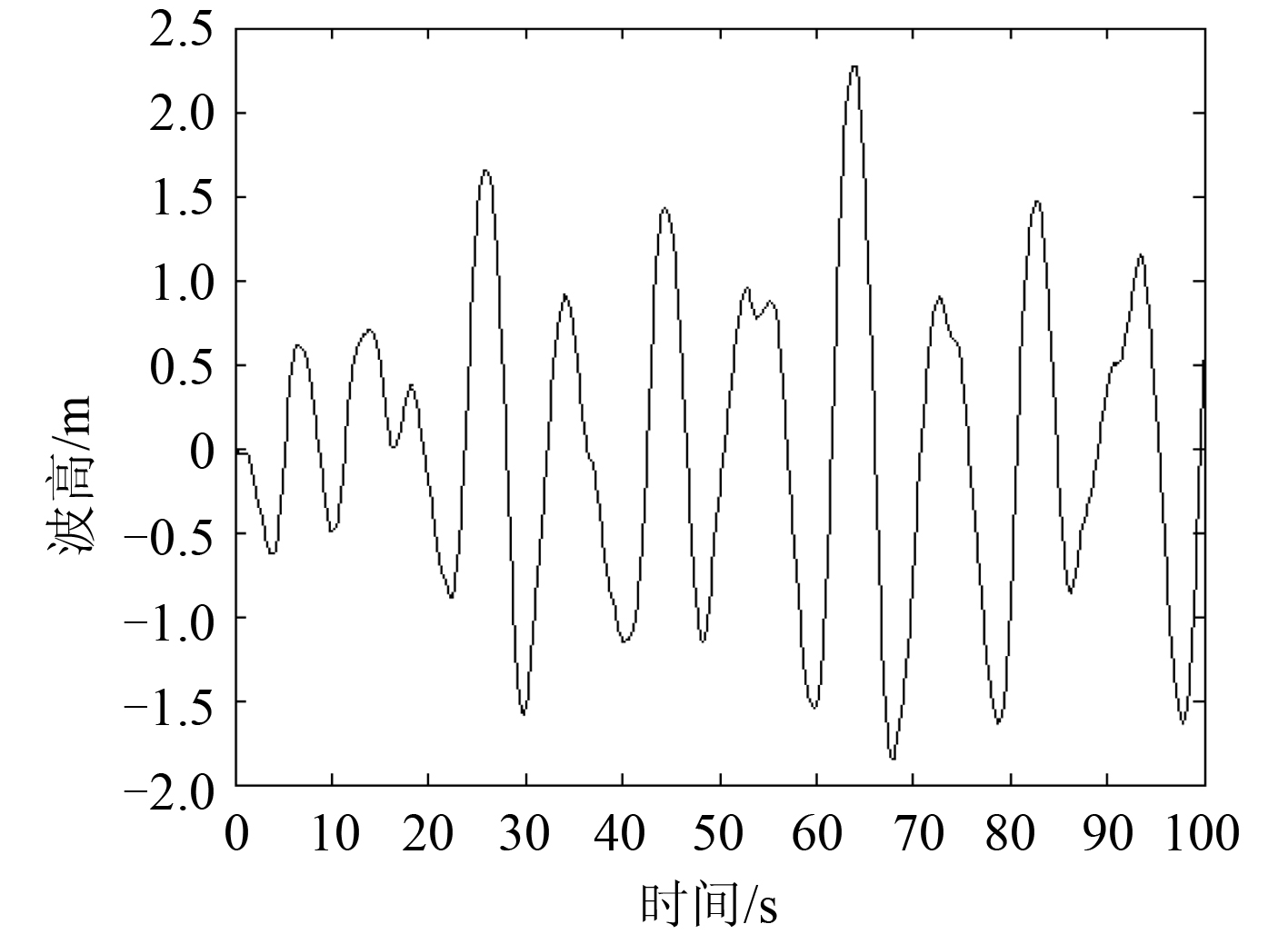
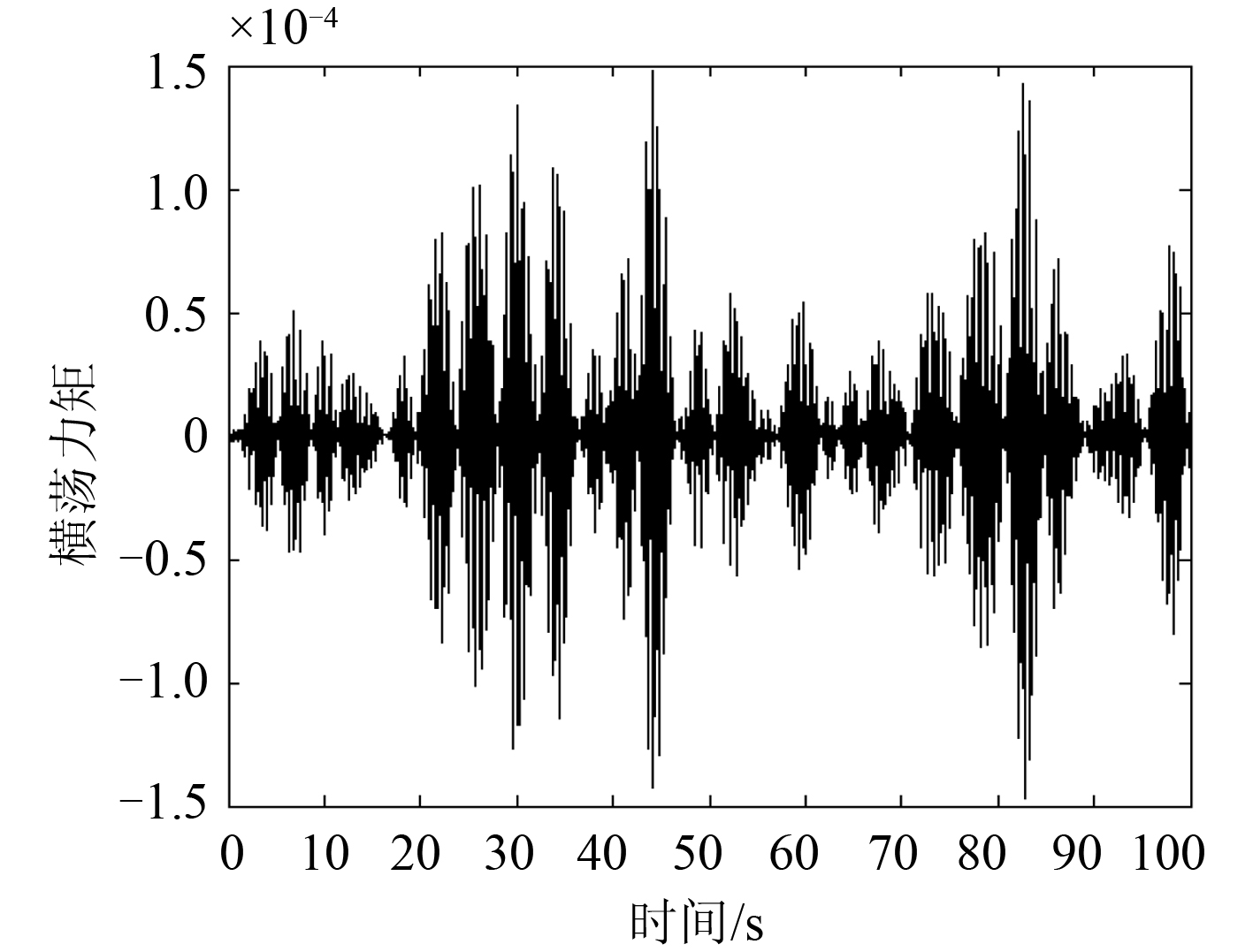
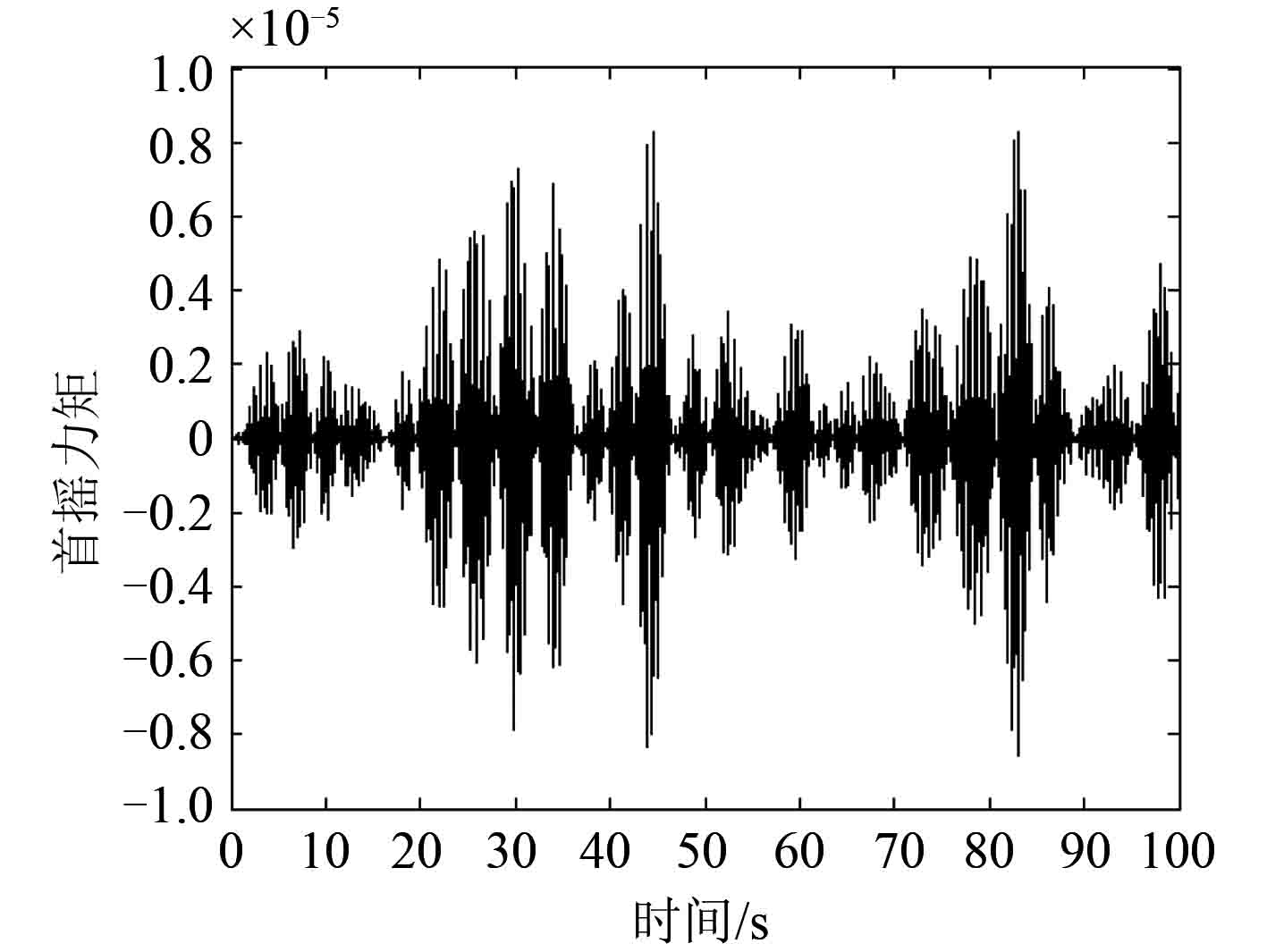
以长峰波模拟波浪的运动,波浪时间曲线见图 1。结合长峰波模拟波浪曲线,对该舰艇横荡力模拟且无因次化计算,得到曲线如图 2 所示。计算首摇干扰力矩且无因次化计算,得到曲线如图 3 所示。
|
图 1 波浪曲线 Fig. 1 Wave line |
|
图 2 横荡力矩 Fig. 2 Sway moment |
|
图 3 首摇力矩 Fig. 3 Raw moment |
为更好地分析船舶在不同海浪下的作用扰动分析,考虑在不同遭遇角情况下相同频域内作用力的变化,结合频谱分析方法对时间序列数值进行快速傅里叶变换,得到不同情况下的横荡力频谱及幅值变化。从图4对比可知,在不同海浪遭遇角的前提下,干扰力在同段频域下,频谱幅值形态趋势较为一致,但幅值大小有一定的变化。由于输入海浪是由不同频率的谐波组成,从图中可知在一定频段内,干扰力呈现出 1~2 个尖峰现象,这也反映出干扰力在不同频率下波浪复合作用的结果,符合模拟波浪的仿真输入情况。
虽然船舶与海浪的遭遇角不同,由于受到同段频域的海浪作用,船舶干扰力在频域的形态特性是一致的,这符合计算输入的设定情况。
由于海洋中波浪的长峰波是由多频的谐波组成,舰艇干扰力主要受到波浪力作用;由频谱分析可清晰看出干扰力的主要作用频段,与长峰波输入波浪的作用频段符合,因此该计算方法较好地反应了舰艇在波浪作用下的干扰力仿真结果。
本文从理论仿真角度,模拟计算了船舶在不同谐波频率组合作用下的波浪干扰力变化情况,后续将根据船舶实际在波浪中运动情况进一步对比验证。

|
图 4 频谱分析 Fig. 4 Spectral analysis |
本文从舰艇在海洋环境中运动的角度出发,基于不规则长峰波的数值计算,提出了舰艇在波浪干扰力下的数值计算方法,结合频谱分析,分析了干扰力的作用规律,这为后续实船计算及验证的提供了思路。
| [1] | 陶尧森. 船舶耐波性[M]. 上海: 上海交通大学出版社, 1985. |
| [2] | 苏兴翘. 船舶操纵性[M]. 北京: 国防工业出版社, 1981. |
| [3] | 文圣常, 余宙文. 海浪理论与计算原理[M]. 北京: 科学出版社, 1984. |
| [4] | 刘应中, 缪国平. 船舶在波浪上的运动理论[M]. 上海: 上海交通大学出版社, 1986. |
 2017, Vol. 39
2017, Vol. 39
