喷水推进是有别于螺旋桨的一种特殊船舶推进方式[1],它在高速高性能船舶中应用广泛。喷水推进泵是喷水推进装置的核心部件,它的性能好坏直接影响到整体推进效率。喷水推进泵的设计要求较苛刻,如效率高、体积小、转速高、抗汽蚀性能强等,喷水推进泵的设计难度较常规水泵要大得多[2]。
Allison[3] 回顾了喷水推进泵的发展历史,包括一维理论、二维理论和近期发展起来的三维理论及升力面理论,他预言:随着计算机计算能力的提高,泵设计过程中的水动力问题将会更多地采用仿真手段来解决,从而可减少对物理模型的依赖。Tan[4] 提出了一种给定环量分布的三维有势流动计算方法,用置于叶片中心的涡面代替叶片对水流的作用。Borges[5] 在相同设计条件下用常规方法和三维方法设计了 2 个叶轮,结果是三维方法得到的叶轮具有较高的效率和较宽的高效区。Bonaiuti[6] 总结了三维设计中各参数对喷水推进泵的效率和汽蚀性能的影响规律。
在国内,喷水推进泵的设计主要依靠一维或二维方法,往往需要大量试验和反复修改才能得到满足要求的叶片形状,国内喷水推进泵的设计手段亟待改进。本文分析某喷水推进船未达到设计航速的原因,开展三维理论和 CFD 方法在喷水推进泵导叶设计中的应用研究,分析轴面形状和喷口直径对导叶及整个喷水推进泵性能的影响,最终优化设计导叶使喷水推进泵的推力提高约 5%。
1 导叶对喷水推进器推力的影响喷水推进器是利用喷出水流的反作用力推动船舶前进的。建立喷水推进与船体的控制体如图 1所示,依据动量原理可得推力表达式为:

|
图 1 “喷水推进器+船体”系统[7] Fig. 1 Control volume of waterjet-hull system |
| $T = m{V_{out}} - m{V_{in}} = \rho Q({V_{out}} - {V_{in}})\text{,}$ | (1) |
式中:m 为质量流量;ρ 为水密度;Q 为体积流量;Vout 为平均喷射速度;Vin 为平均来流速度。对于理想喷水推进而言Vin =Vship ,则推力公式变为:
| $T = \rho Q({V_{out}} - {V_{ship}})\text{。}$ | (2) |
可见,Vout 为影响喷水推进推力的最关键因素。
喷水推进的射流为不可压缩的轴对称旋转射流。根据圆柱坐标系下的雷诺方程,忽略粘性应力及紊动的正压力项,可得下列简化的基本微分方程组:
轴向x 方向的运动方程:
| $u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial r}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + \frac{1}{{\rho r}}\frac{{\partial r{\tau _x}}}{{\partial r}}\text{,}$ | (3) |
式中
连续性方程:
| $\frac{{\partial ru}}{{\partial x}} + \frac{{\partial rv}}{{\partial r}} = 0\text{,}$ | (4) |
将上式两端各乘ρr,并积分得:
| $\int_0^\infty {\rho u\frac{{\partial u}}{{\partial x}}} r{\rm d}r \!\!+\!\! \int_0^\infty {\rho rv\frac{{\partial u}}{{\partial r}}} {\rm d}r \!=\! - \!\! \int_0^\infty {\frac{{\partial p}}{{\partial x}}r{\rm d}r} \!+\! \!\int_0^\infty {\frac{{\partial r{\tau _x}}}{{\partial r}}} {\rm d}r\text{,}$ | (5) |
式中:
| $\int_0^\infty {\rho u\frac{{\partial u}}{{\partial x}}} r{\rm d}r = \frac{1}{2}\frac{{\rm d}}{{{\rm d}x}}\int_0^\infty {\rho {u^2}} r{\rm d}r\text{,}$ | (6) |
| $\begin{split}\\[-12pt]\int_0^\infty {\rho vr\frac{{\partial u}}{{\partial r}}} {\rm d}r = \left| {\rho uvr} \right|_0^\infty - \int_0^\infty {\rho u\frac{{\partial (rv)}}{{\partial r}}}{\rm d}r = \\ 0 + \int_0^\infty {\rho u\frac{{\partial (ru)}}{{\partial x}}} {\rm d}r = \frac{1}{2}\frac{{\rm d}}{{{\rm d}x}}\int_0^\infty {\rho {u^2}r} {\rm d}r\text{,}\end{split}$ | (7) |
| $\int_0^\infty {\frac{{\partial p}}{{\partial x}}} r{\rm d}r = \frac{{\rm d}}{{{\rm d}x}}\int_0^\infty p r{\rm d}r\text{,}$ | (8) |
| $\int_0^\infty {\frac{{\partial r{\tau _x}}}{{\partial r}}}{\rm d}r = \left| {r{\tau _x}} \right|_0^\infty = 0\text{,}$ | (9) |
故式(5)变形为:
| $\frac{{\rm d}}{{{\rm d}x}}\int_0^\infty {(p + \rho {u^2})} r{\rm d}r = 0\text{。}$ | (10) |
式(10)表示压强与轴向动量通量之和沿x 方向守恒,如导叶整流效果不理想,将有部分能量转化为压力能,不产生推力[8]。
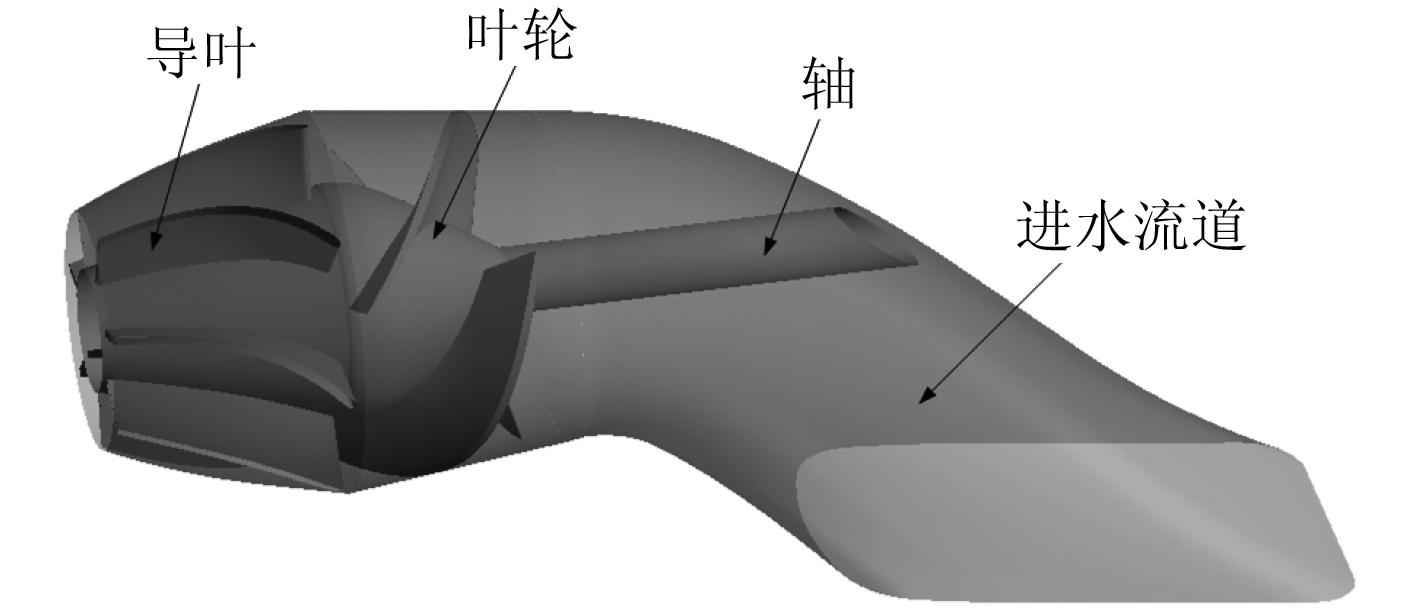
某型喷水推进器的结构如图 2所示,它装船后未能达到设计航速。图 3 给出了 CFD 计算得到的原导叶出口流线图,可见,由于导叶内壁线型使得导叶出口流线很不直,一部分旋转动能不能产生推力。采用周向动能与轴向动能的比值来定量考察导叶的整流性能[9]:
| $C = \left( {{H_{Vc}}/{H_{Va}}} \right) \times 100\% \text{,}$ | (11) |
周向动能定义为:
| ${H_{Vc}} = u_c^2/2g\text{,}$ | (12) |
轴向动能定义为:
| ${H_{Va}} = u_a^2/2g\text{。}$ | (13) |
式中:uc 为平均周向速度;ua 为平均轴向速度。C 值越小说明整流效果越好。该喷水推进器原导叶出口的周向速度与轴向速度的比值为 0.16。
|
图 2 某喷水推进器结构 Fig. 2 A certain waterjet configuration |

|
图 3 导叶出口的流线 Fig. 3 Streamlines throughout waterjet stator |
本文采用一种基于势流理论的三维反设计方法[10],流场被认为无旋且定常,叶片骨面以一系列的涡代替,其强度通过速度环量 2πrVθ 控制(Vθ 是圆周平均速度),通过迭代求解抛物线形偏微分方程得到最终叶片形状。需要输入参数有:1)叶轮的轴面形状,包括轮毂、轮缘和叶片的进、出口边;2)转速、叶片数,导叶的转速为 0;3)流体属性;4)进口压力;5)设计流量;6)叶片厚度;7)各轴面流线上的包角分布;8)叶片进、出口边的涡强度(即环量
| ${p^ + } - {p^ - } = \left( {2\rm{\pi} /B} \right)\rho {W_{mbl}}\partial \left( {r{V_\theta }} \right)/\partial m\text{。}$ | (14) |
式中:B 为叶片数;Wmbl 为相对轴面速度。
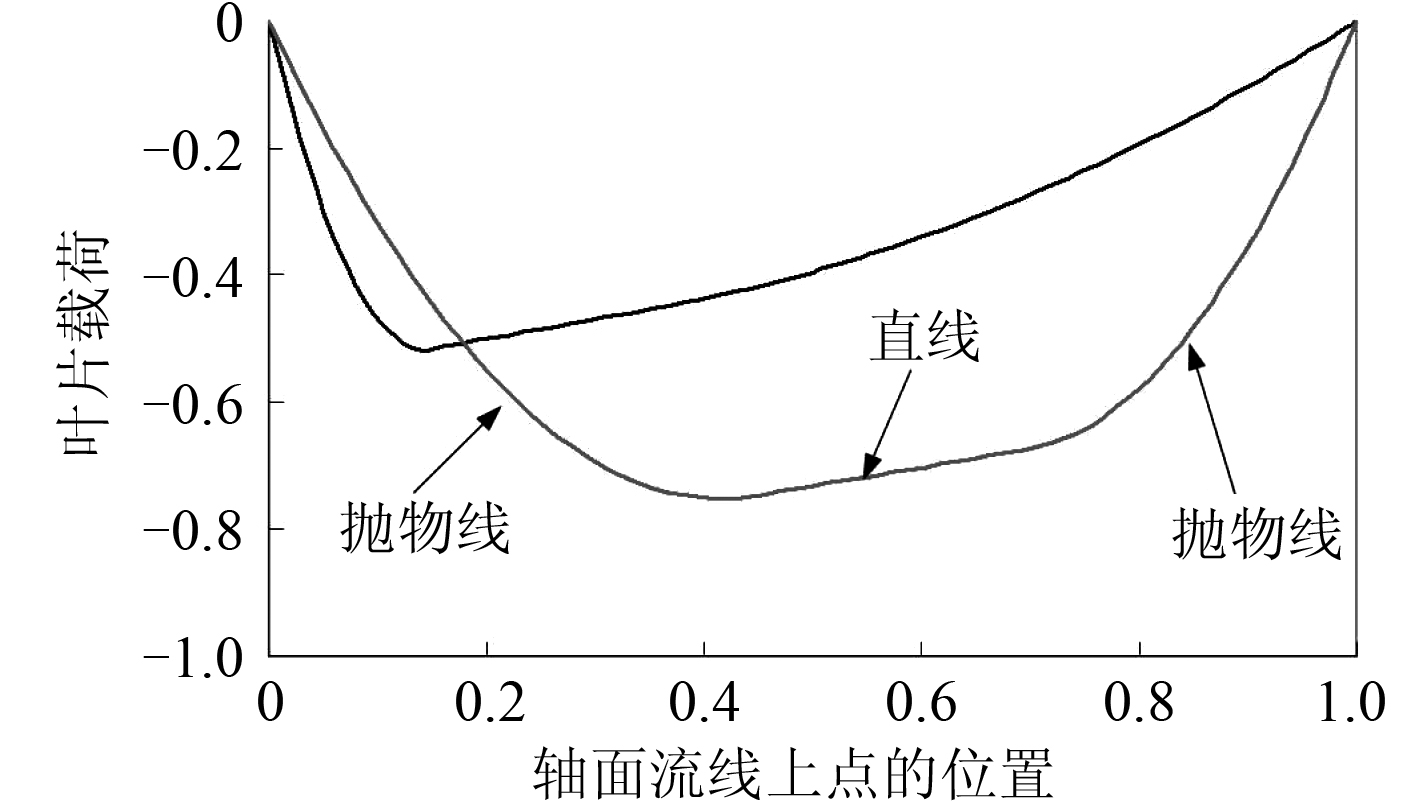
采用分段函数来描述叶片载荷的分布形式如图 4所示,由 2 段抛物线和一段直线组成,调整NC 和ND 的大小可方便控制载荷分布规律。为了避免导边冲击和随边脱流,导边和随边处的载荷都设为 0。
|
图 4 叶片载荷参数分布规律 Fig. 4 Definition of blade loading parameter |
采用基于单元中心的有限体积法来求解雷诺时均方程,选择 SST 剪切应力输运模式来对湍流进行模拟,它在边界层边缘和自由剪切层采用κ-ε 模式,在靠近固体壁面的区域采用κ-ω 湍流模式,两者之间通过一个混合函数来过渡。
叶轮内部流动处于旋转坐标系下,对应的质量方程和动量方程为[10]:
| $\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot (\rho {V}) = 0$ | (15) |
| $\frac{D}{{Dt}}(\rho {V}) \!+\! 2\rho {\omega} \!\times\! {V} \!+\! \rho {\omega} \times {\omega} \! \times \! {r} \!=\! \rho {f} \!-\! \nabla P \!+\! (\mu \!+\! {\mu _t}){\nabla ^2} {V}\text{,}$ | (16) |
式中:f 为质量力,水流从船底吸入管道时势能改变,故水流的重力也应考虑在内;P 为流体旋转对应的压力;μ 为海水的动力粘性系数;μt 为湍流动力粘性系数。
导叶体和进流管道内部流动处于固定坐标系下,质量方程与叶轮内流场一样,动量方程变为:
| $\frac{D}{{Dt}}(\rho {V} ) = \rho {f} - \nabla P + (\mu + {\mu _t}){\nabla ^2}{V} \text{。}$ | (17) |
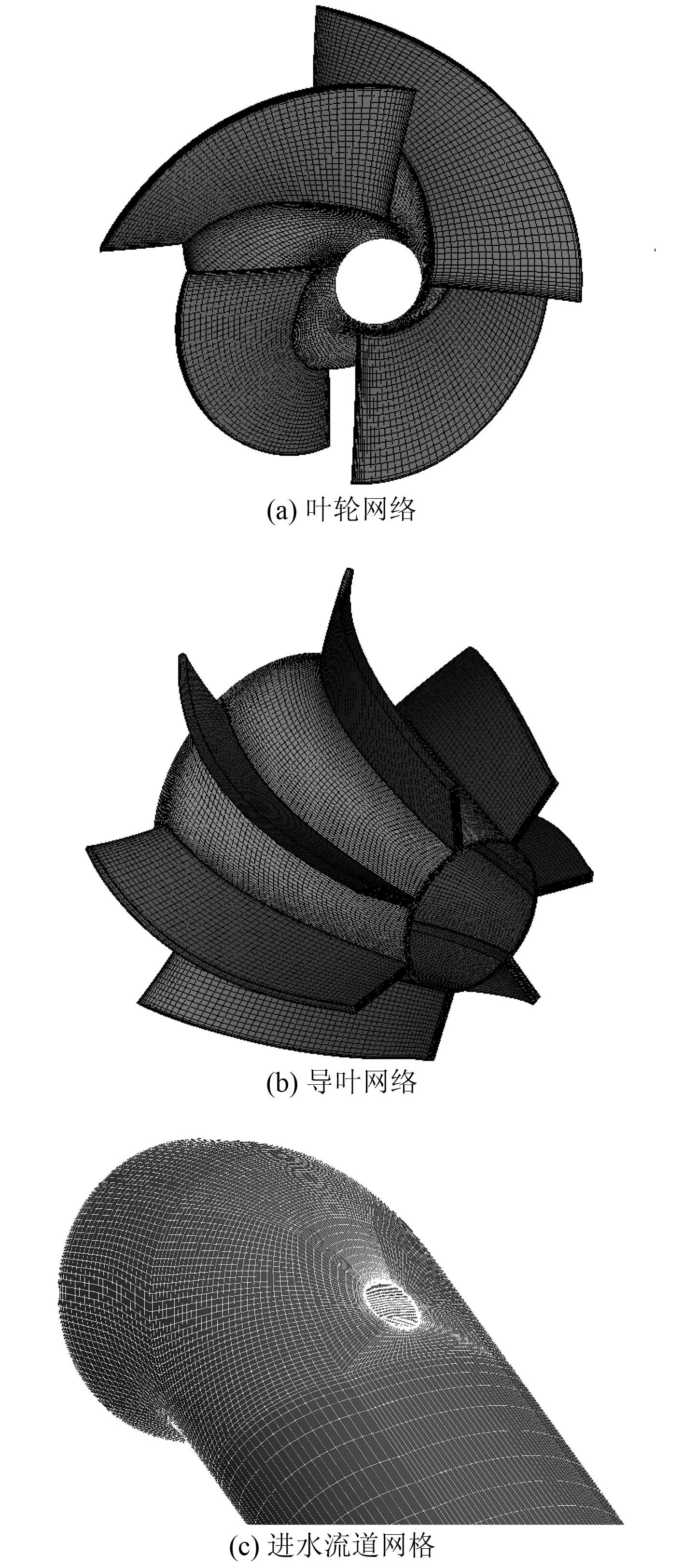
考虑到船底边界层对进流的影响,在喷水推进器下方建立 1 个足够大的流场域,如图 5所示。叶片周围嵌入 O 型网格进行加密,保证了网格正交性和质量。在导边、随边及叶顶间隙附近都进行了网格加密。进水流道采用分块六面体结构化网格划分,在进水流道壁面、轴及船底附近添加了 10 层三棱柱网格,以使y+ 满足湍流模型的要求。整个计算域的网格为 117 万。各部件网格如图 6所示。

|
图 5 喷水推进计算域 Fig. 5 Computational domain of waterjet propulsion |
|
图 6 各部件网格 Fig. 6 Mesh of each part of waterjet |
船底流场的两侧和靠近船头的来流面设为速度进口;喷口压力和船底出流压力设为环境压力;导叶壁面、进水流道壁面、船底等设为无滑移壁面;叶轮外壳设为绝对静止壁面,叶轮的轮毂和叶片设为相对静止壁面。基于 Ansys CFX 软件求解速度与压力的耦合方程,采用稳态多参考系方法。
4 导叶的优化设计MJP 和 KaMeWa 公司的导叶多采用轮毂收缩成一点的形式,本文导叶优化设计也采用了该类结构。若设计航速时通过喷水推进泵的流量与喷水推进泵最高效率点的流量基本一致,可认为“船-泵-机”实现了较好匹配。参照文献[10],为了优化叶轮通道内二次回流,导叶的载荷分布为轮毂载荷比轮缘载荷更靠前。轮毂流线上 NC,ND 和 SLOPE(SLOPE 为直线斜率)设为 0.15,0.3 和 0.1,轮缘流线上 NC,ND 和 SLOPE 设为 0.45,0.7 和 0.1。图 7 给出了喷口直径为 124 mm 时的叶片形状。图 8 是其内部流线,其周向动能与轴向动能的比值为 0.04,整流效果较原导叶有了大幅提高。

|
图 7 喷口直径为 124 mm 时的的导叶形状 Fig. 7 Stator shape with nozzle diameter 124 mm |

|
图 8 通过喷口直径 124 mm 导叶的流线 Fig. 8 Streamlines throughout the retrofitted stator |
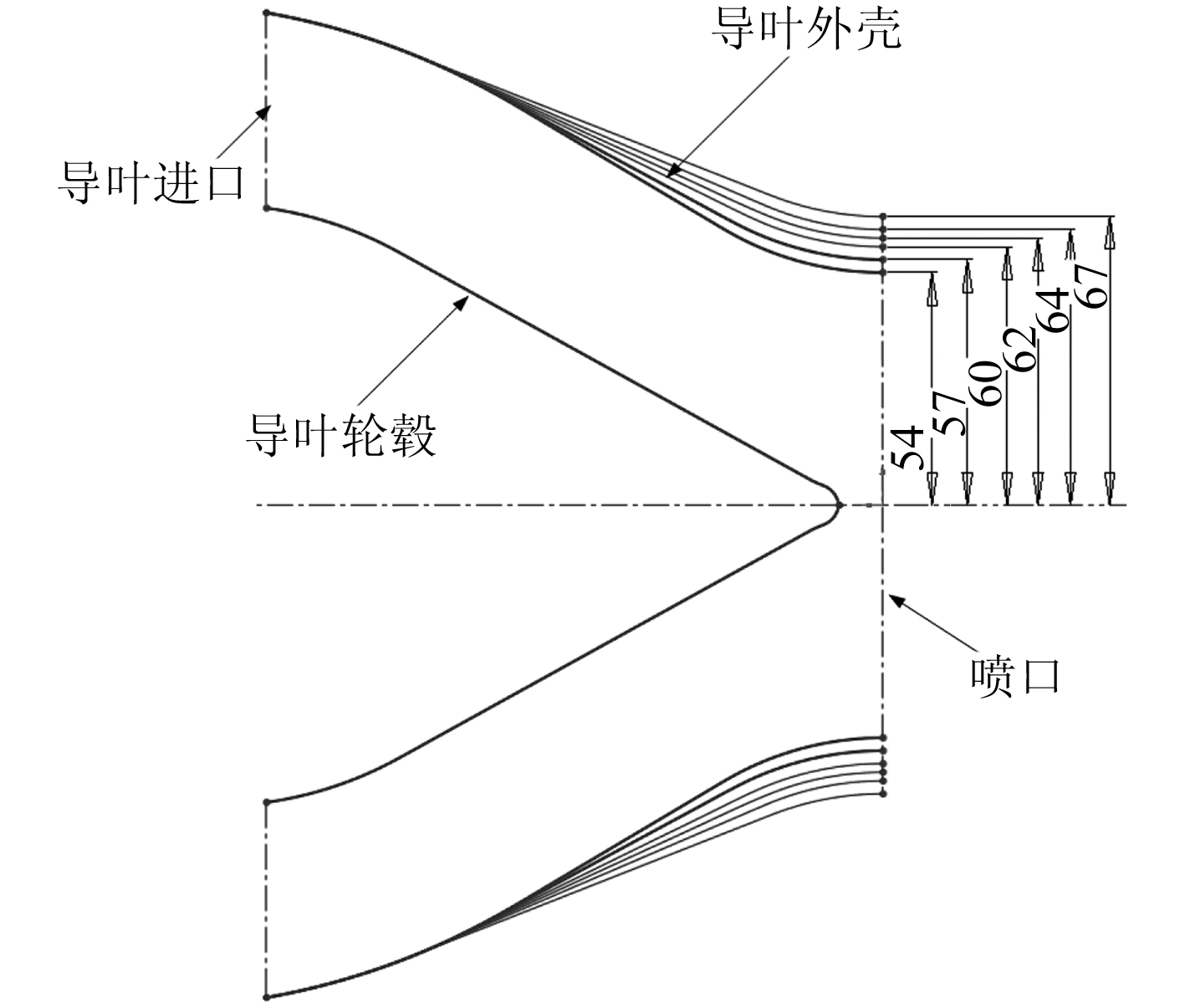
喷口直径是影响通过喷水推进泵流量的一个重要因素,它直接关系到Vout 的大小。为了选出最优喷口直径以实现“船-泵-机”的较好匹配,建立了 6 个不同喷口直径的轴面轮廓,如图 9所示。
|
图 9 六型不同喷口直径的轴面轮廓 Fig. 9 Sketch of stator meridional channel |
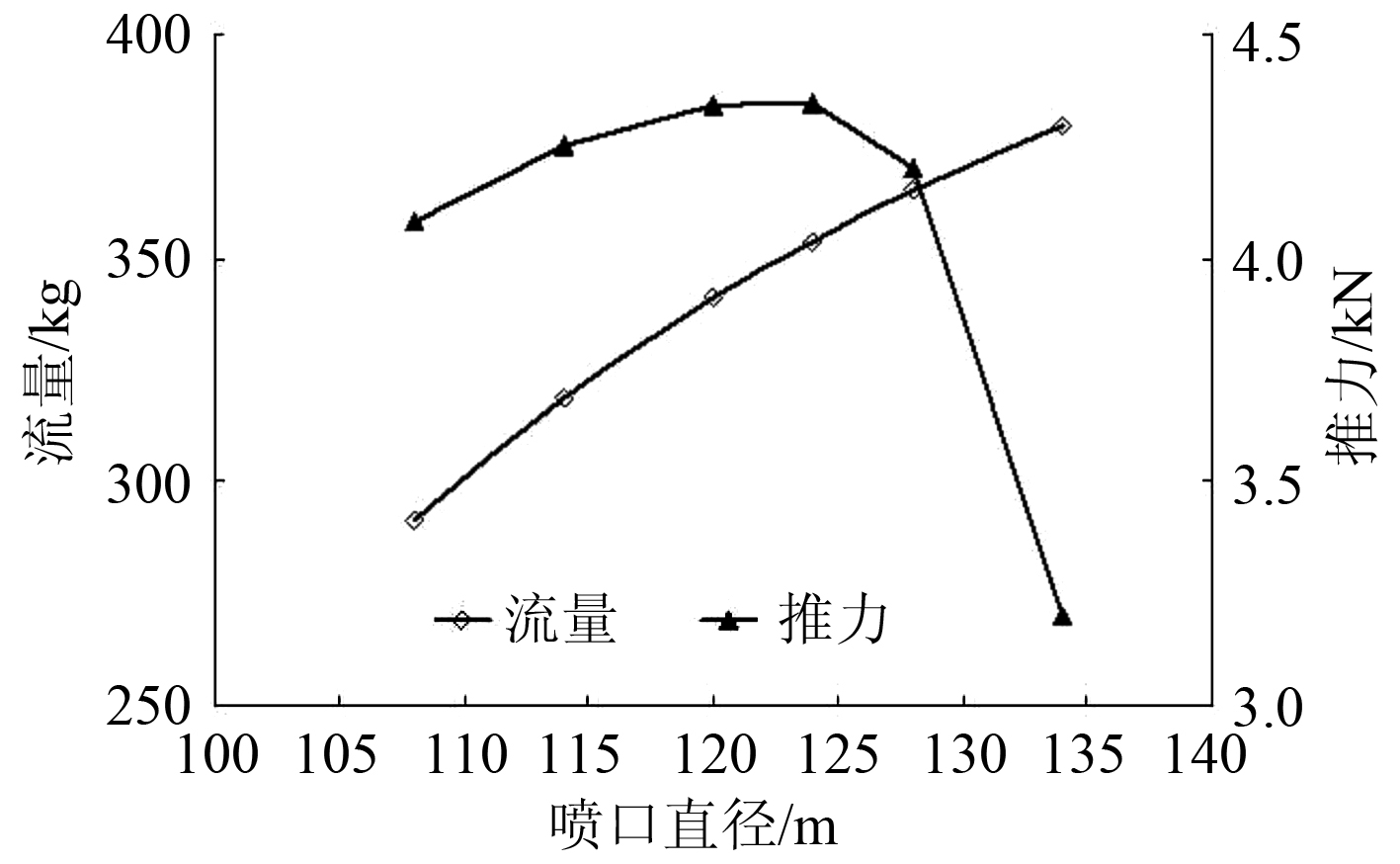
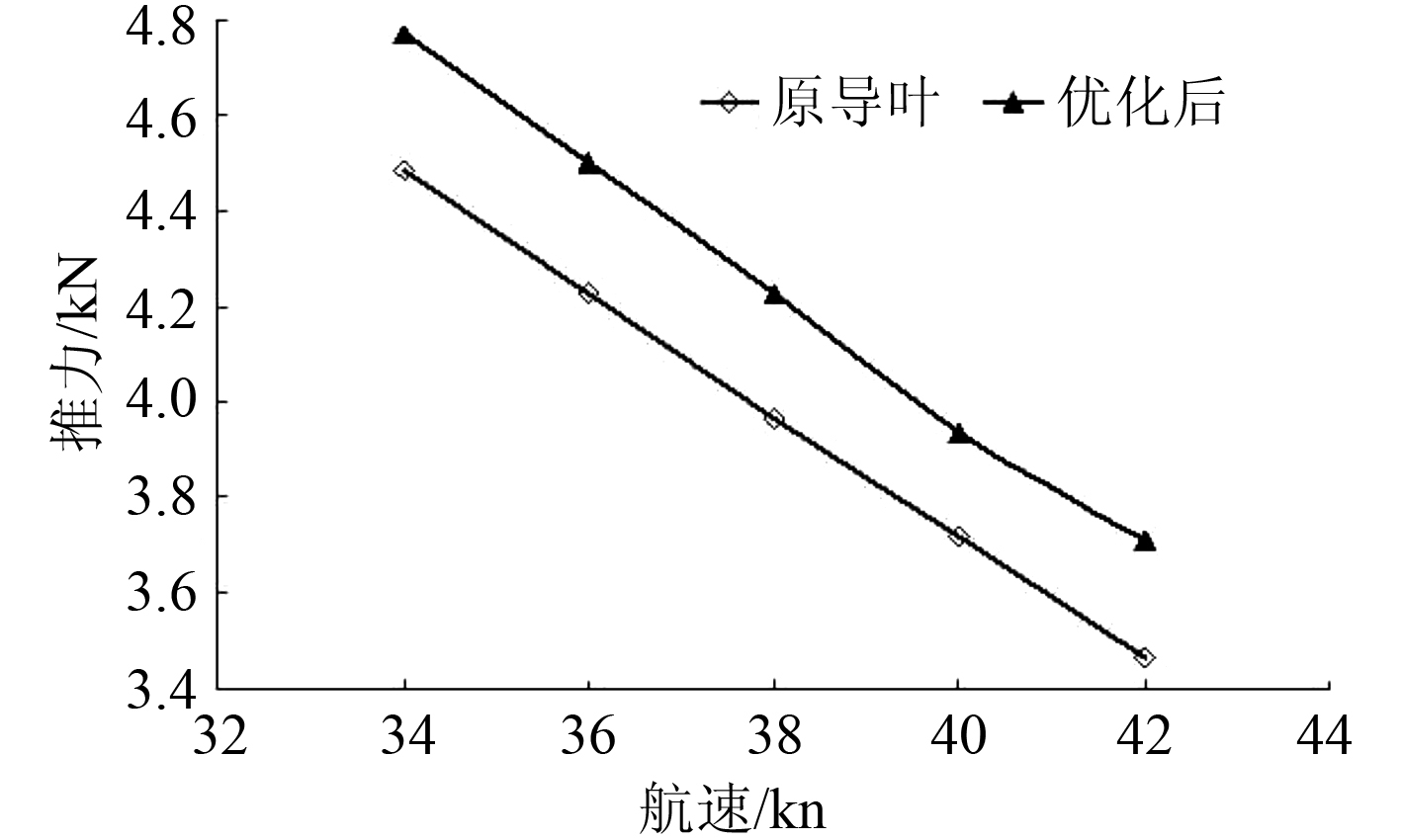
图 10 给出了不同喷口直径时通过喷水推进泵的流量和喷水推进泵产生的推力。流量随喷口直径的增大而增大,推力随喷口直径的增大呈先增大后减小的趋势。当喷口直径为 124 mm 时推力最大,此时通过喷水推进泵的流量恰好与喷水推进泵最高效率点的流量相差不大,都约为 350 kg/s。图 11 给出了原导叶与改型导叶后喷水推进泵的推力,在各个航速工况下改型后导叶的推力都要比原导叶大约 5%。
|
图 10 不同喷口直径时的流量和推力 Fig. 10 Comparison of mass flow rate and thrust when different nozzle diameters |
|
图 11 原型导叶与改型导叶的推力对比 Fig. 11 Thrust curves of the original waterjet and the optimized waterjet |
本文基于三维理论和 CFD 工具,探讨了一种叶片设计方法在喷水推进泵导叶设计中的应用,导叶片形状通过给定轴面轮廓和环量分布规律后迭代计算得出。建立了描述喷水推进泵内流场的数值模型,经对 6 个喷口直径条件下通过喷水推进泵的流量和喷水推进泵产生的推力进行比较,选取出了最优喷口直径,实现了“船-泵-机”的最佳匹配。改型导叶的整流效果较原导叶有了较大改善,使各个航速下喷水推进泵的推力提高了约 5%。本文结果表明,三维理论和 CFD 工具可在喷水推进泵导叶设计中发挥重要作用。
| [1] | WANG Yong-sheng, DING Jiang-ming. Research on the relationship between waterjet power absorption and vessel speed[C]// International Conference on Waterjet Propulsion 4. London, UK: The Royal Institution of Naval Architects (RINA), 2004. |
| [2] | ZANGENEH M, DANESHKHAH K. A multi-objective automatic optimization strategy for design of waterjet pumps[C]// International Conference of Waterjet Propulsion 5. London, UK: The Royal Institution of Naval Architects (RINA), 2008. |
| [3] | ALLISIN J L, JIANG C, STRICKER J G. Modern tools for waterjet pump design and recent advance in the field[C]// International Conference on Waterjet Propulsion 2. Amsterdam, The Netherlands: The Royal Institution of Naval Architects (RINA), 1998. |
| [4] | TAN C S, HAWTHORNE W R, WANG C. Theory of blade design for large deflection, Part II, annular cascades[J]. Journal of Engineering for Gas Turbines and Power, 1984, 106: 354–365. |
| [5] | BORGES J E. A three-dimensional inverse method for turbomachinery: Part I-theory[J]. Journal of Turbomachinery, 1990, 112: 347–354. |
| [6] | BONAIUTU D, ZANGENEH M, AARTOJARVI R. Parametric design of a waterjet pump by means of inverse design, CFD calculations and experimental analyses[J]. ASME Journal of Fluids Engineering, 2010, 132: 1–15. |
| [7] | TERWISGA V. Report of the specialist committee on validation of waterjet test procedures to the 24th ITTC[C]// The 24th International Towing Tank Conference. Edinburgh, UK: ITTC, 2005: 471–508. |
| [8] | 孙存楼. 喷水推进器与螺旋桨混合推进舰船推进性能研究[D]. 武汉: 海军工程大学, 2011. |
| [9] |
刘承江, 王永生, 王立祥. 采用CFD方法的喷水推进轴流泵导叶整流性能改进研究[J]. 船舶力学, 2010, 14(5): 466–471.
LIU Cheng-jiang, WANG Yong-sheng, WANG Li-xiang. Research on commutating effect optimization of waterjet axial-flow pump stator based on CFD method[J]. Journal of Ship Mechanics, 2010, 14(5): 466–471. |
| [10] | GOTO A, ZANGENEH M. Hydrodynamic design of pump diffuser using inverse design method and CFD[J]. Journal of Fluids Engineering, 2002, 124: 319–328. |
 2017, Vol. 39
2017, Vol. 39
