现实中的结构与理想状态相比,必然存在着缺陷损伤,在船舶与海洋工程中把这类情况统称为初始缺陷。很多存在初始缺陷的船舶与海洋工程结构在服役期间发生了灾难性事故,不仅严重危害工作人员的人身安全,而且造成了巨大的经济损失。因此为了反映结构的真实状态,在校核其极限承载力时要考虑初始缺陷的影响。
目前结构的非线性有限元已经成为结构极限强度分析的重要手段,且被认为是目前极限强度分析最有效的方法,当建模技术足够准确时,能给出准确的分析结果。有限元法另一个重要的优点在于可以方便地分析任意形式结构的极限强度,并可考虑初始缺陷及任意复杂加载的影响,这是本文选取该方法进行结构极限强度分析的重要原因[1]。
船体的初始缺陷包括凹陷、初始变形和残余应力。张婧等[2]研究计算了具有初始变形的船体加筋板结构在复杂受力状态下的极限强度,表明初始缺陷的存在将削弱结构的极限强度。任慧龙等[3]基于固有应变的等效载荷模拟焊接残余应力,并同时考虑初始挠度,对船体梁的极限强度进行分析。Paik和 saad[4 –5]研究了含凹陷钢板的压缩极限强度,考虑凹陷的形状、尺寸和位置等因素的影响。Cui 等[6]的研究表明,初始变形的形状,即半波数对极限强度影响较大。这些结果多为一种初始缺陷对极限强度的影响研究。
本文将同时考虑 3 种初始缺陷。初始变形主要有 3 种类型,即板型初始变形、加筋侧移型初始变形和加筋梁柱型初始变形,残余应力选取的是焊接残余应力及凹陷变形。以单筋单跨加筋板模型为研究对象,考虑初始变形,3 种不同半径及 4 种不同速度的撞击球所形成的凹陷对结构极限强度的影响,并同时考虑 3 种缺陷同时存在的情况,对加筋板结构的极限强度进行研究,为进一步研究复杂结构的极限强度提供参考。
1 初始缺陷 1.1 初始变形加筋板结构初始挠度相当复杂,本文假设的初始缺陷为结构的屈曲变形模式。对商船焊接产生的初始挠度的进行统计研究发现,加筋板初始变形的挠度可由多个半波组成的曲线表示,初始变形可表现为加筋侧移型初始变形、加筋梁柱型初始变形和板型初始变形。
板型初始变形方程为:
| ${{{w}}_p} = \left( { - {w_p}} \right) \times \cos \frac{{m\pi x}}{a} \times \cos \frac{{n\pi y}}{b}\text{,}$ | (1) |
式中:wp =b/200 为加筋板格初始变形幅值,b 为加筋间距。
加筋侧移型初始变形方程为:
| ${{{w}}_{oh}} = \left( { - {w_{os}}} \right) \times \cos \frac{{m\pi x}}{a} \times \sin \frac{{n\pi z}}{{2h}}\text{,}$ | (2) |
式中:wos =a/1 000 为加筋侧移型初始变形幅值 。
加筋梁柱初始挠曲方程为:
| ${{{w}}_{oh}} = \left( { - {w_{oc}}} \right) \times \cos \frac{{n\pi x}}{a}\text{。}$ | (3) |
式中:woc =a/1 000 为考虑加筋垂直方向的梁柱型初始变形幅值。
1.2 焊接残余应力焊接残余应力形成的主要原因是构件在焊接过程中由于受到集中热输入,导致温度场不断变化,从而引发了塑性变形。当构件冷却后,在焊缝处产生拉应力,而在远离焊缝部位产生压应力。
在进行极限强度计算时,残余应力作为一种已有的状态存在,即残余应力处理为结构的初始应力。首先把残余应力编成初应力文件输入到 Ansys 中前,要先得到加筋板单元的初应力。单元初应力是通过加载计算把残余应力分布公式赋予到单元上[7]。
1.3 凹陷船舶在其生命周期内会发生各种损伤,外物损伤是其中的一种形式,它可能是通过货物的不正当装载卸载而产生的。当船体加筋板被外物撞击时,凹陷等缺陷就会产生。
Paik[8]经过研究和分析发现:在凹陷的幅值一定的情况下,凹陷形状对板格极限强度的影响很小。因此,本文加筋板上的所有凹陷全由球撞击而成。采用显式有限元程序 LS-DYNA 进行球与加筋板的碰撞过程的模拟,得出结构所有节点的位移改变量,选取加筋板结构的碰撞模型作为含凹陷结构极限强度的分析模型。
2 计算模型在研究含初始缺陷加筋板结构极限强度中,选取了单筋单跨计算模型,如图 1 所示,尺寸如表 1 所示。材料的弹性模量E = 2.1E5 MPa,泊松比γ = 0.3,屈服强度σy = 315 MPa。在单筋单跨模型中,凹陷所选取的位置在翼板 1/4 处;考虑撞击球速度和直径对形成凹陷的影响,球的速度定义为 10 m/s,选取的半径有 0.2 m,0.25 m 和 0.3 m;球的半径定义为 0.3 m,速度有 8 m/s,9 m/s,10 m/s 和 11 m/s。
|
图 1 加筋板计算模型 Fig. 1 Calculation model of stiffened panel |
|
|
表 1 加筋板几何尺寸 Tab.1 Dimensions of stiffened panel |
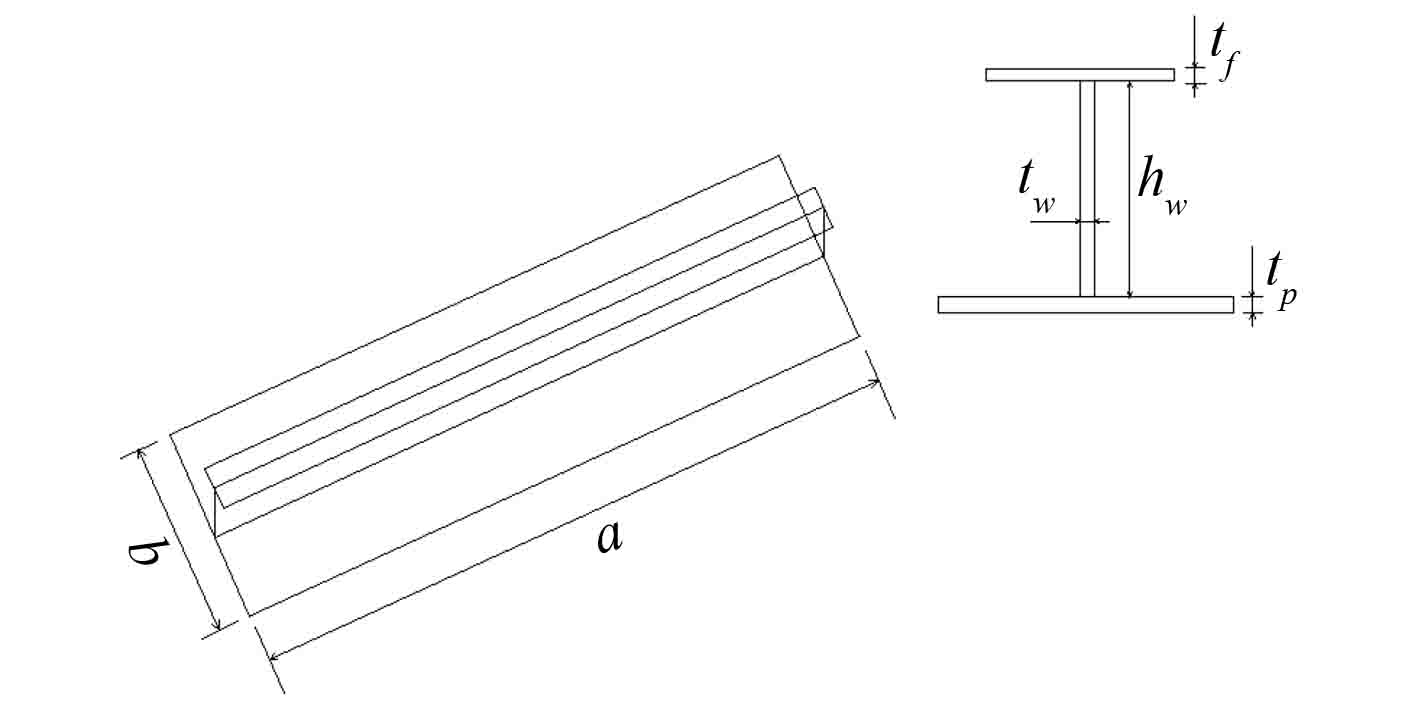
初始变形选取的是 3 种初始变形的叠加,即板型初始变形、加筋侧移型初始变形和加筋梁柱型初始变形的叠加。图 2 为含初始变形的加筋板的变形和应力云图。从图中可看出,应力较大的范围主要集中在加强筋和板格中部区域,在压缩载荷作用下加强筋发生显著弯曲变形,板格中间也因为挤压发生褶皱变形。
|
图 2 含初始变形的加筋板变形和应力云图 Fig. 2 Deformation and the stress distribution of stiffened plate with initial deformation |
凹陷的形成考虑的是撞击球半径的不同,即 0.2 m,0.25 m,0.3 m,3 种半径下的最大凹陷深度分别是 5.056 6 mm,7.315 2 mm 和 10.332 mm。图 3~图 5 分别为半径为 0.2 m,0.25 m 和 0.3 m 的撞击球所形成的凹陷,以及凹陷和初始变形同时存在时加筋板结构的变形及应力云图。从图中可看出,腹板在轴向压缩载荷下产生了扭转变形,而且凹陷及其衔接处相对于翼板其他部位产生了较大的应力。对于腹板部分,由于受到球的撞击,与凹陷连接的腹板部分有明显的突起,这部分是腹板承载力最薄弱的地方,应力较大。对比 3 种情况不难发现,突起越严重,腹板发生屈曲的范围越小。在加筋板板格部分,含初始变形的加筋板板格部分有明显的凹凸变形,只含凹陷的加筋板虽然板格部分应力维持在较高的水平,但没有屈曲变形。这表明初始变形和凹陷的存在,在不同程度上改变了加筋板结构的变形和应力分布情况。

|
图 3 加筋板的变形和应力云图(半径为 0.2 m) Fig. 3 Deformation and the stress distribution of stiffened plate(Radius of 0.2 m) |

|
图 4 加筋板的变形和应力云图(半径为 0.25 m) Fig. 4 Deformation and the stress distribution of stiffened plate(Radius of 0.25 m) |

|
图 5 加筋板的变形和应力云图(半径为 0.3 m) Fig. 5 Deformation and the stress distribution of stiffened plate(Radius of 0.3 m) |
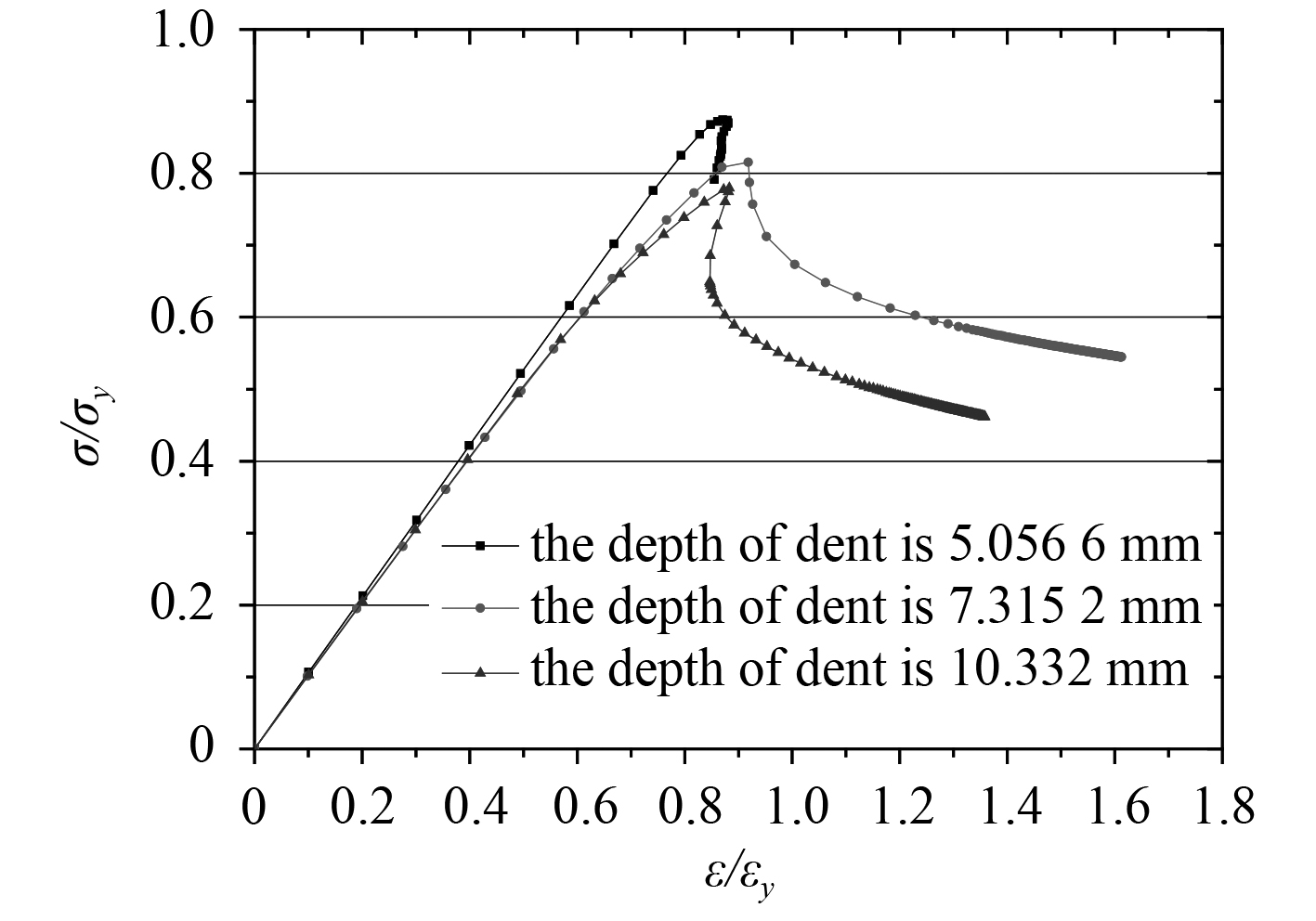
图 6和图 7 分别为 3 种初始缺陷时加筋板的应力-应变曲线图(不同的撞击球半径)。从图中可看出,无量纲应力-应变曲线在结构达到极限承载力前呈线性上升状态,压缩载荷一旦达到结构的极限承载力,曲线就迅速下降。只含初始变形结构的承载力大,只含凹陷的次之,含两者叠加的最小,但后两者的承载力变化不大,这表明相对于初始变形,凹陷对结构的承载力影响更大,而且缺陷叠加对结构极限强度的影响大于单独考虑初始变形或者凹陷的情况。从图 7 和表 2 可知,在同一个速度的情况下,随着撞击球半径的增加,凹陷深度越大,加筋板的极限承载力逐渐减小。

|
图 6 含初始缺陷加筋板的应力-应变曲线图 Fig. 6 The stress-strain curves of stiffened panels under initial imperfections |
|
图 7 不同凹陷深度的加筋板应力-应变曲线 Fig. 7 The stress-strain curves of stiffened panels under different dent depths |
|
|
表 2 含初始缺陷加筋板的极限强度 Tab.2 Ultimate strength of stiffened panel with initial imperfections |
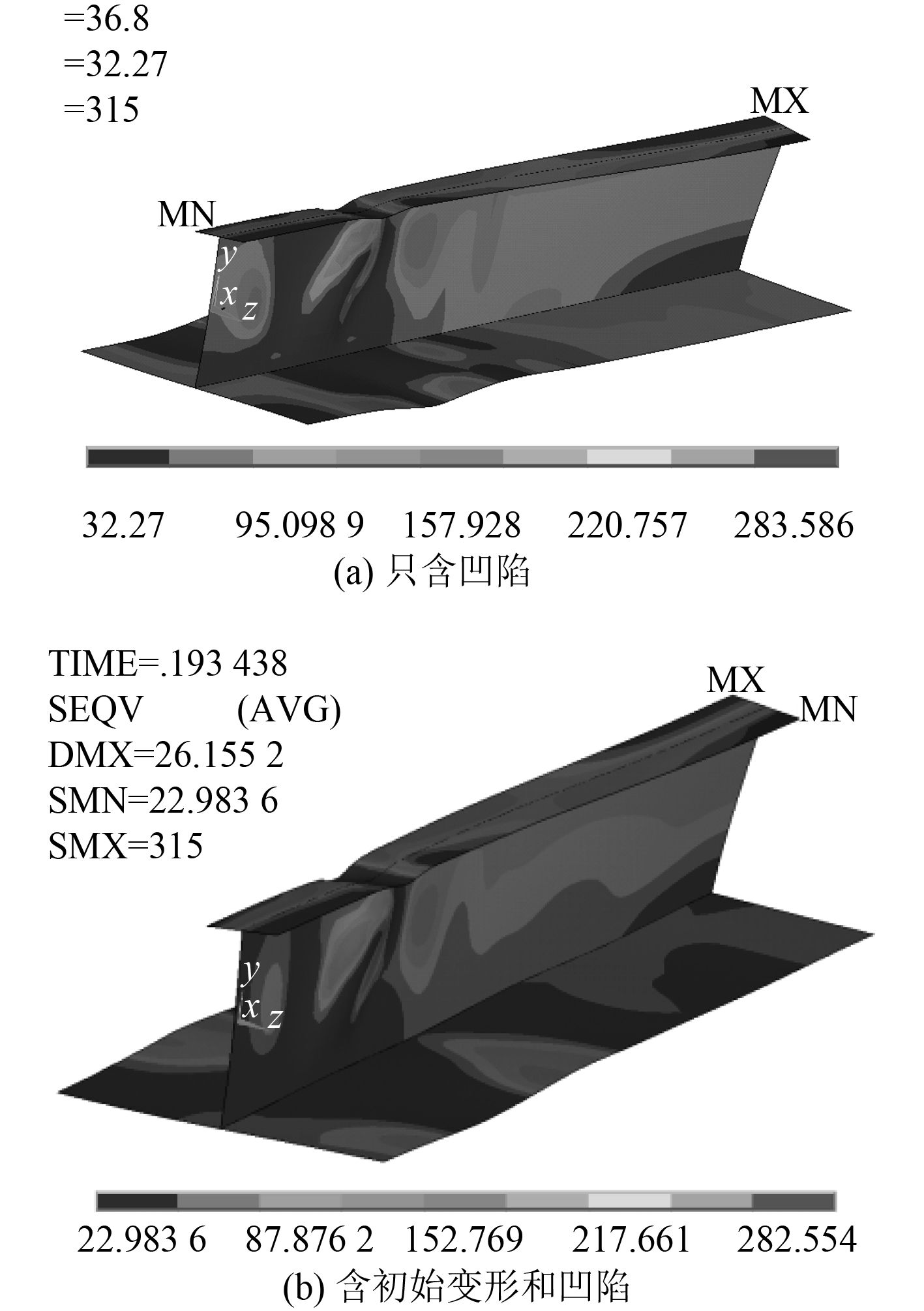
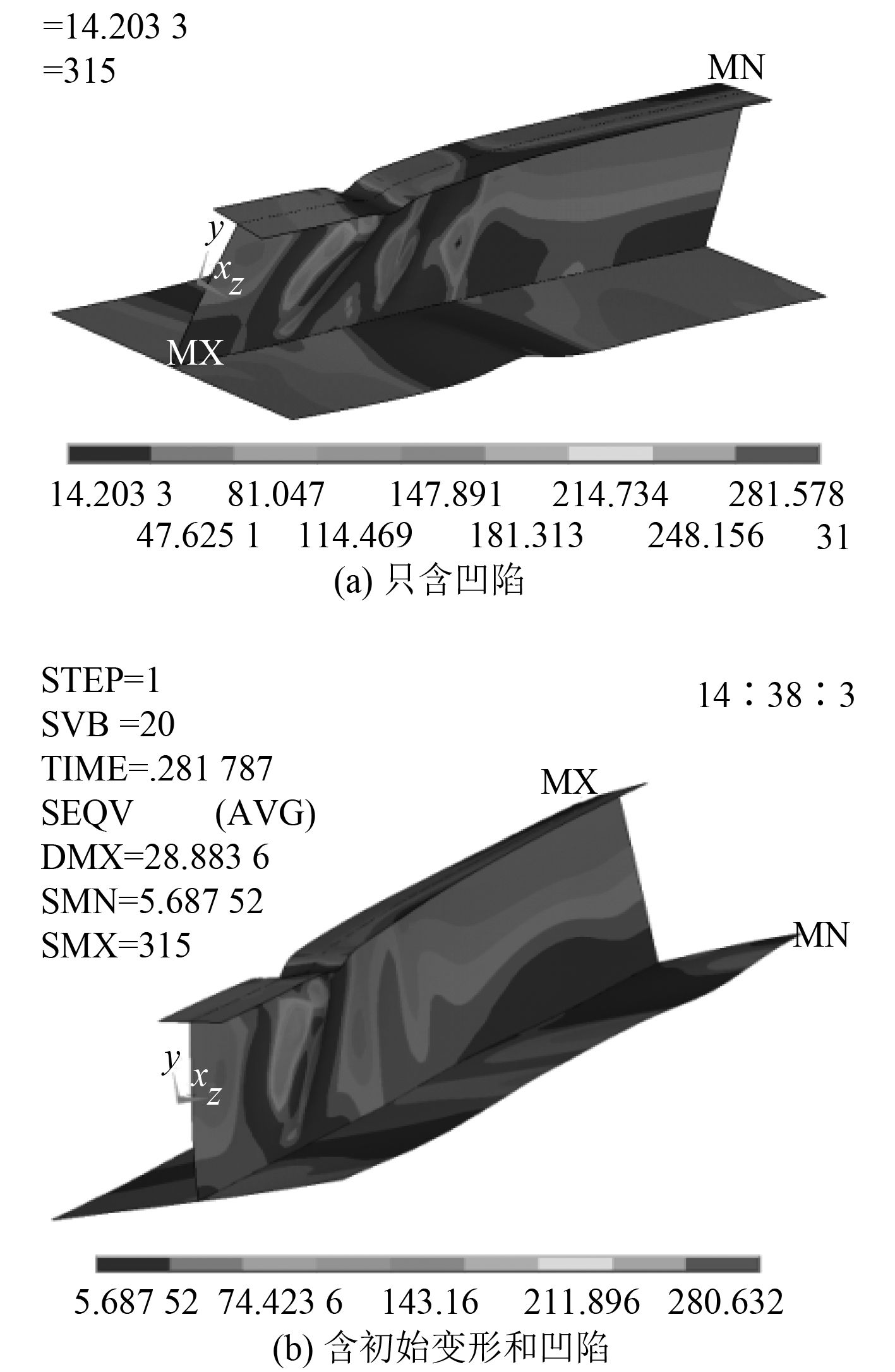
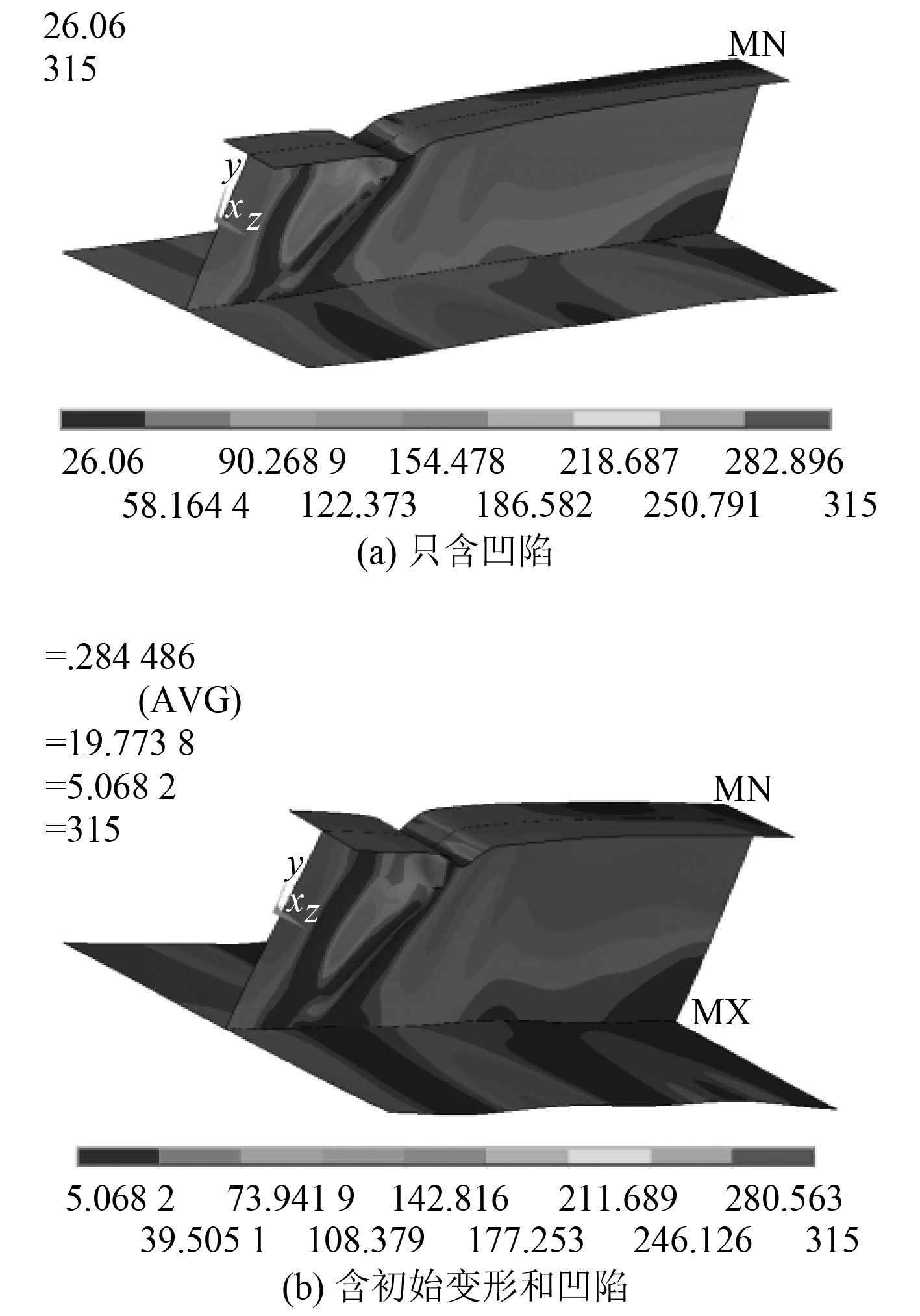
凹陷的形成考虑的是撞击球自由落体时速度的不同,即 8 m/s,9 m/s,10 m/s,11 m/s,4 种情况下的最大凹陷深度分别是 7.436 9 mm、10.223 5 mm、10.332 mm 和 16.114 6 mm。图 8~图 10 分别为不同速度的撞击球所形成的凹陷,以及凹陷和初始变形同时存在时加筋板结构的变形及应力云图。从图中可看出,在压缩载荷作用下,由于凹陷缺陷的存在,凹陷部位及凹陷衔接处应力较大;相对于只含凹陷的加筋板结构,含凹陷和初始变形的加筋板的应力分布范围更广;板格初始变形改变了加筋板板格部分变形和应力分布情况,板格塑性区的范围大于只含凹陷的加筋板。在轴压作用下,腹板与凹陷衔接处褶皱变形严重,加强筋也随着凹陷深度的增加扭转程度增大。在整个加载过程中,翼板后半段所承受的应力水平较小,与凹陷所在的前半段应力较大的现象有明显的差距。这表明,初始缺陷的存在改变了结构的应力分布特点,因此在校核结构强度时,必须考虑初始缺陷的影响。
|
图 8 加筋板的变形和应力云图(速度为 8 m/s) Fig. 8 Deformation and the stress distribution of stiffened plate(velocity of 8 m/s) |
|
图 9 加筋板的变形和应力云图(速度为 9 m/s) Fig. 9 Deformation and the stress distribution of stiffened plate(velocity of 9 m/s) |
|
图 10 加筋板的变形和应力云图(速度为 11 m/s) Fig. 10 Deformation and the stress distribution of stiffened plate(velocity of 11 m/s) |
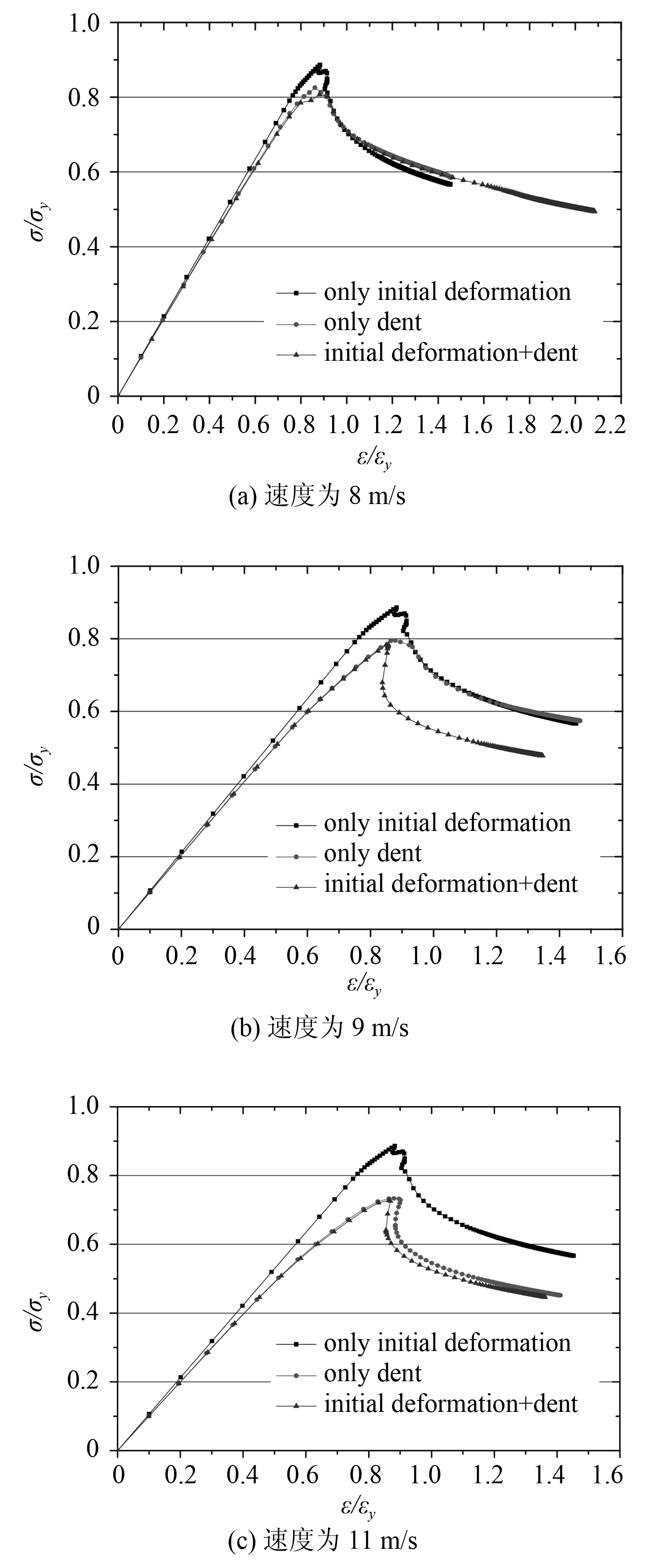
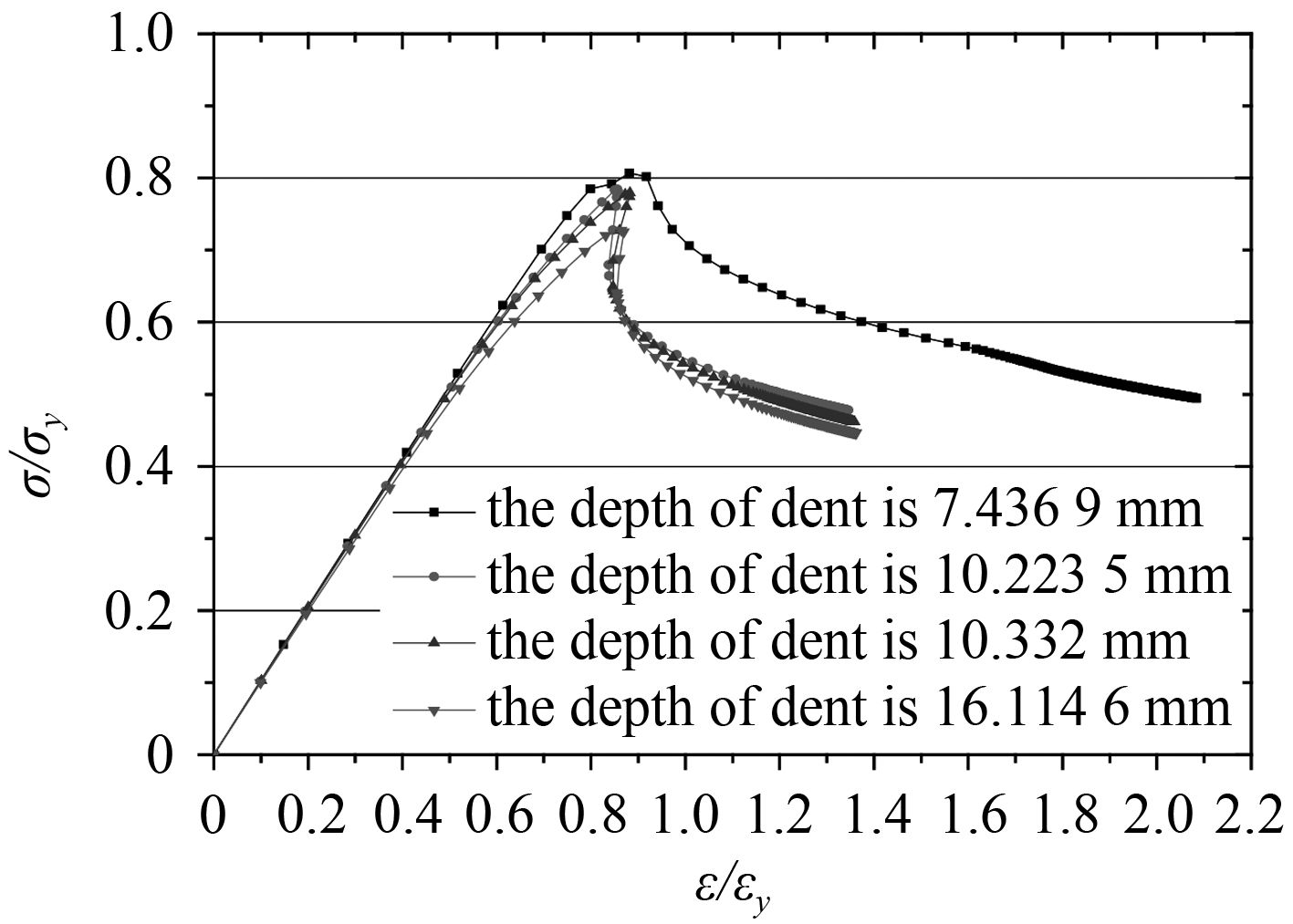
图 11和图 12 分别为 3 种初始缺陷时加筋板的应力-应变曲线图(不同的撞击球速度)。从图中可看出,曲线的变化趋势与考虑重量影响的相似,只含初始变形结构的承载力最大,只含凹陷结构和含凹陷和初始变形结构的承载力相近。在 4 种凹陷深度下,凹陷越深,结构的承载力越小。这些变化趋势在表 3 中也可看出。这表明,初始缺陷的存在降低了结构的承载力,凹陷缺陷对结构极限强度的影响大于初始变形的影响。
|
图 11 含初始缺陷加筋板的应力-应变曲线图 Fig. 11 The stress-strain curves of stiffened panels under initial imperfections |
|
图 12 不同凹陷深度的加筋板应力-应变曲线 Fig. 12 The stress-strain curves of stiffened panels under different dent depths |
|
|
表 3 含初始缺陷加筋板的极限强度 Tab.3 Ultimate strength of stiffened panel with initial imperfections |
考虑初始变形、残余应力和凹陷同时存在时,加筋板极限强度的承载能力将会大幅度的减弱。对各种因素单独作用和联合作用下加筋板极限强度的影响进行分析。
图 13 为含初始缺陷加筋板的变形和应力云图。从图中可看出,加筋板结构由于都含有初始变形,在轴压作用下,板格和腹板都出现不同程度的褶皱屈曲现象。所不同的是,在含有凹陷的加筋板中,凹陷所在的翼板发生扭转,而且凹陷及其附近的应力较大。在含有残余应力的加筋板中,由于残余应力赋给了加筋板所有的结构,所以在轴压初期,整个加筋板的应力水平均较高,随着单轴压缩载荷的不断增加,载荷大部分由加筋板的前半部分承受,这部分的弯曲变形也越来越严重。这表明初始缺陷的存在,都不同程度地改变了加筋板结构的应力分布和屈曲变形模式。

|
图 14 为含初始缺陷的加筋板无量纲应力-应变曲线图。从图中可看出,含不同初始缺陷的加筋板结构所能承受的最大应力不同。含初始变形和含凹陷的加筋板承载力较大,含残余应力的承载力较小。同时也可看出,初始缺陷的叠加对加筋板结构的承载力影响明显大于初始缺陷单独存在的情况。在应力-应变曲线图中,加筋板结构在轴压开始阶段的承载力呈线性状态,当模型达到极限承载力后,曲线就迅速下降。这表明加筋板结构在达到极限承载力后结构发生屈曲破坏,其承载力迅速减弱。
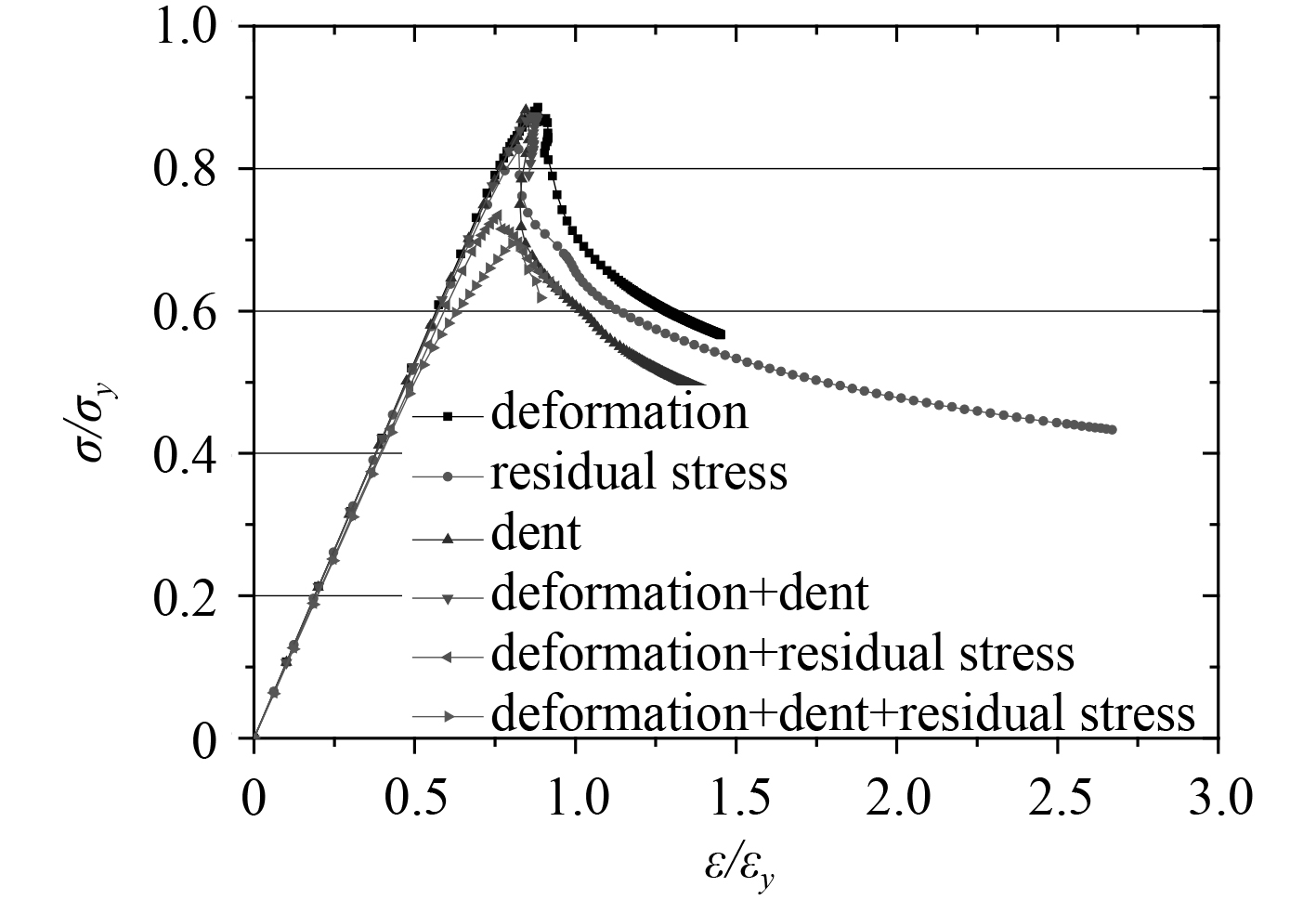
|
图 14 含初始缺陷的加筋板应力-应变曲线图 Fig. 14 The stress-strain curves of stiffened panels with initial imperfections |
表 4 为含初始缺陷加筋板的极限强度。从表中可看出,含初始变形和凹陷加筋板的极限强度值相差无几,但显著大于含残余应力的极限强度,它们的差值大于 6%。加筋板结构中考虑的初始缺陷种类越多,其极限强度值越小,而且结构中考虑了残余应力的极限强度明显小于没有考虑的,初始缺陷的存在降低了结构的承载力,这提醒我们,在校核结构承载力时,应该全面考虑结构现实中存在的初始缺陷,以保证结构的安全性和真实性。
|
|
表 4 含初始缺陷加筋板的极限强度 Tab.4 Ultimate strength of stiffened panel with initial imperfections |
本文通过有限元软件 Ansys,考虑在轴向压缩载荷作用下初始缺陷对加筋板极限强度的影响研究,得出以下结论:
1)在考虑初始变形和凹陷对加筋板结构极限强度影响时发现,初始变形对结构的承载力影响最小,而凹陷对结构的承载力影响相对较大,凹陷对结构的承载力随着凹陷深度的增大而减小;
2)在考虑 3 种初始缺陷的影响时发现,残余应力严重影响结构的承载力,6 种模式下的结构只要含有残余应力,其承载力明显小于不含残余应力的。而在建造 FPSO 过程中所用的钢材都会经过焊接,这必然会在结构中残留残余应力,因此在校核结构强度时,不能忽视残余应力的影响;
3)初始缺陷的叠加对结构承载力的影响明显大于单独存在的情况。因此结构在建造运输等过程中,应该尽量避免在同一结构上造成缺陷的叠加,最大限度地保持结构的完整性。
| [1] | 张婧, 江小龙, 石晓彦, 等. 具有初始缺陷的裂纹加筋板剩余极限强度分析[J]. 哈尔滨工程大学学报. 2016, 37(7): 1–9. |
| [2] | 张婧, 施兴华, 顾学康. 具有初始缺陷的船体加筋板结构在复杂受力状态下的极限强度研究[J]. 中国造船. 2013, 54(1): 60–70. |
| [3] |
任慧龙, 郎舒妍, 任晨辉, 等. 带有初始缺陷的船体结构极限强度研究[J]. 舰船科学技术, 2015, 37(12): 38–41.
REN Hui-long, LANG Shu-yan, REN Chen-hui, et al. Ultimate strength of hull structure with initial defect[J]. Ship Science and Technology, 2015, 37(12): 38–41. |
| [4] | PAIK J K, LEE J M, LEE D H. Ultimate strength of dented steel plates under axial compressive loads[J]. International Journal of Mechanical Sciences. 2003, 45(3): 433–448. |
| [5] | SAAD-ELDEEN S, GARBATOV Y, GUEDES SOARES C. Ultimate strength analysis of highly damaged plates[J]. Marine Structures, 2016, 45: 63–85 |
| [6] | CUI W, MANSOUR A E. Effects of welding distortions and residual stresses on the ultimate strength of long rectangular plates under uniaxial compression[J]. Mar Struct 1998(11): 251–269. |
| [7] | 汤夕春. 残余应力对H型钢梁柱构件极限承载力影响研究[D]. 武汉: 武汉理工大学, 2006. |
| [8] | PAIK J K. Ultimate strength of dented steel plates under edge shear loads[J]. Thin-Walled Structures. 2005, 43: 1475–1492. |
 2017, Vol. 39
2017, Vol. 39
