人类对海上油气开发已有 60 年的历史,海洋平台的工作水深已由浅海拓展至深水海域。工作于深水海域的平台包括深水多功能半潜平台(SEMI)、张力腿平台(TLP)及浮式生产储油船(FPSO)及浮式生产钻井储油装置(FDPSO)[1]。在这些不同类型的海洋平台中,FDPSO 集石油钻探与生产功能于一体,这极大地缩短了石油开采的周期,提高了工作效率,降低前期作业成本,使其成为深海油田开采的理想平台。
FDPSO 长期工作于深水海域,通过锚链系统来提供船体运动响应的恢复力。但FDPSO 受风浪影响比较大,对浪向角也比较敏感,抵抗恶劣海况的能力差。为了提高钻井船的工作效率,对其进行深入的水动力性能研究十分必要。
目前,一些学者针对锚链线参数对浮式平台响应的影响开展了相关研究。通过对某半潜式平台的多点系泊系统的研究,Smith 等[2] 和 Radwan 等[3]给出了锚链系统设计的相关图表。基于静态优化理论,XU 等[4]研究了截断后系泊系统的参数对半潜式平台运动响应的影响。Chen 等[5]研究了不同水深下 Spar 平台的运动性能。Luis 等[6]应用非线性动力学研究了多点锚泊系统的水动力性能。Montasir 等[7]研究了对称和不对称的锚链布置对 Spar 平台的动态响应的影响。
根据国内外的研究现状可知,仅有一少部分的学者考虑了锚链预张力与船体运动响应的关系,因而本文将着重研究这一方面。文中采用 Ansys AQWA 时域耦合计算模块,对船体运动响应和锚链预张力进行计算,并将计算结果与试验结果进行对比。为了进一步考虑锚链预张力的影响,采用4种不同的系泊系统,并分别计算运动响应,分析比较其异同。
1 理论基础 1.1 绕射/辐射力本文假设流体是理想无旋流体,适用于势流理论,并且假设作用于浮体上的入射波是微幅波,流体的运动可以用速度势
| ${\varPhi} (x,y,z,t) = \varphi (x,y,z){e^{ - i\omega t}} \text{,}$ | (1) |
根据势流理论,势函数可以分解为入射势、绕射势和辐射势。
| $\phi (x,y,z){e^{ - i\omega t}} = \left[ {\left( {{\phi _I} + {\phi _d}} \right) + \sum\limits_{j = 1}^6 {{\varphi _j}{x_j}} } \right]{e^{ - i\omega t}} \text{,}$ | (2) |
式中:ϕI 为入射波势;ϕd 为绕射波势;ϕj 为j 模态下的辐射势;xj 为单位波幅下j 态的运动;ω 为入射波频率。
流场中一点(x,y,z)的入射势为:
| ${\phi _I} = \frac{{ - ig\cosh [k(d + z)]{e^{ik(x\cos \theta + y\sin \theta )}}}}{{\omega \cosh (kd)}} \text{,}$ | (3) |
式中:d 为水深;k 为波数;θ 为浪向(0° 为顺着x 轴方向)。
通过求解流域内满足边界条件的边界积分方程,可以求出速度势,进而通过伯努利方程求得一阶水动力压力分布为:
| $p = - \rho \frac{{\partial \Phi }}{{\partial t}} \text{,}$ | (4) |
通过对浮体湿表面压力积分,可以得到流体作用力。水动力可以分解成入射力和绕射力。作用力表达为:
| ${{F}} = - i\rho \omega {e^{ - i\omega }}\iint_{{S_B}} {\left( {{\phi _I} + {\phi _D}} \right){{n}}{\rm d}S} \text{,}$ | (5) |
式中:SB 为湿表面面积; n 为浮体表面单位法向量。
由于船体运动产生的辐射力为:
| ${F_{ji}} = - \rho {\omega ^2}\iint\nolimits_{{S_B}} {{\phi _i}{n_j}{\rm d}S} , i,j = 1,2...6 \text{,}$ | (6) |
进一步分解为:
| ${F_{ji}} = {\rm{ - }}{A_{ji}}{\ddot x_i} - {B_{ji}}{\dot x_i} \text{,}$ | (7) |
式中:Aij 为附加质量系数;Bij 为阻尼系数。
| $F\left( \omega \right) = {F_j} + {F_{ji}} \text{,}$ | (8) |
| ${M_s}\left( \omega \right)\ddot x + {M_a}\left( \omega \right)\dot x + { C}\left( \omega \right)\dot x + {K_s}\left( \omega \right)x = F\left( \omega \right) \text{。}$ | (9) |
式中:x 为单位波幅下的运动(RAO);ω 为入射波频率;F 为浮体受到的波浪力; C 为线性阻尼矩阵。
1.2 二阶平均漂移力二阶平均漂移力对于浮式平台至关重要,应用远场公式可以计算得到[9]。二阶波浪平均漂移力和力矩为:
| $\begin{split}\\[-12pt]{{F}}_{strc}^{(2)} = & - \oint_{WL} {\frac{1}{2}} \rho g\zeta _r^2{{n}}{\rm d}l + {\iint_{{S_0}} {\frac{1}{2}\rho \left| {\nabla \phi } \right|} ^2}{{n}}{\rm d}S +\\& \iint_{{S_0}} {\rho (X \cdot \nabla \frac{{\partial \Phi }}{{\partial t}})} {{n}}{\rm d}S + {M_s}{{R}} \cdot {{\ddot X}_g} \text{,}\end{split} $ | (10) |
| $\begin{split}\\[-12pt]{{M}}_{strc}^{(2)}\! \!=\! & - \oint_{WL} \!\!{\frac{1}{2}} \rho g\zeta _r^2({{r}} \!\times\! {{n}}){\rm d}l \!+\!\!\! {\iint_{{S_0}} \!\!{\frac{1}{2}\rho \left| {\nabla \phi } \right|} ^2}\!\!({{r}} \!\times\! {{n}}){\rm d}S \!+\\& \iint_{{S_0}} {\rho (X \cdot \nabla \frac{{\partial \Phi }}{{\partial t}})} ({{r}} \times {{n}}){\rm d}S + {{{I}}_s}{{R}} \cdot {{\ddot X}_g} \text{。}\end{split}$ | (11) |
式中:WL 为水线长度,ζr
为相对波高,S0 为浮体湿表面,
| $\begin{split}\\[-12pt]{{F}}_{}^{(2)}(t) \!=\! \!& \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N \!\!{\left. {\left\{ \!\!\!\!\!{\begin{array}{*{20}{c}}{P_{ij}^ - \cos [ - ({\omega _i} - {\omega _j})t + ({\varepsilon _i} - {\varepsilon _j})]}\\{ + P_{ij}^ + \cos [ - ({\omega _i} + {\omega _j})t + ({\varepsilon _i} + {\varepsilon _j})]}\end{array}} \right.} \!\!\!\!\!\right\}} }+ \\& \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {\left. {\left\{ \!\!\!\!\!{\begin{array}{*{20}{c}}{Q_{ij}^ - \sin [ - ({\omega _i} - {\omega _j})t + ({\varepsilon _i} - {\varepsilon _j})]}\\{ + Q_{ij}^ + \sin [ - ({\omega _i} + {\omega _j})t + ({\varepsilon _i} + {\varepsilon _j})]}\end{array}} \!\!\!\!\!\right.} \right\}} } \text{,}\end{split}$ | (12) |
其中Pij 和Qij 分别为和频和差频的平方阶传递函数。
| $\begin{split}P_{ij}^ \pm = & - \oint_{WL} {\frac{1}{4}} \rho g{\zeta _i}{\zeta _j}\cos ({\varepsilon _i} - {\varepsilon _j}){{n}}{\rm d}l +\\& \iint_{{S_0}} {\frac{1}{4}\rho \left| {\nabla {\phi _i}} \right|} \left| {\nabla {\phi _j}} \right|{{n}}{\rm d}S+ \\& \iint_{{S_0}} {\frac{1}{2}\rho ({X_i} \cdot \nabla \frac{{\partial {\Phi _j}}}{{\partial t}})} {{n}}{\rm d}S+ \\& \frac{1}{2}{M_s}{{{R}}_i} \cdot {{\ddot X}_{gj}} + \iint_{{S_0}} {\rho \frac{{\partial {\Phi ^2}}}{{\partial t}}} {{n}}{\rm d}S \text{。}\end{split}$ | (13) |
| $\begin{split}\\[-12pt]& [{M_s} + {M_a}\left( t \right)]\ddot x(t) + C\dot x(t) + {K_s}x(t) = \\& {F_{wave}}(t) + {F_{moor}}(t) + {F_{current}}(t) + {F_{wind}}(t) \text{。}\end{split}$ | (14) |
式中: Ms 为 FDPSO 的质量矩阵;Ma (t)为附加质量; C 为阻尼矩阵; x (t)为位移矩阵;Fwave (t)为波浪激励力;Fcurrent(t)和Fwind(t)分别为流载荷和风载荷;Fmoor(t)为锚链力。
2 模型试验 2.1 FDPSO 设计参数在哈尔滨工程大学海洋工程水池开展相关的模型试验,水池长 50 m,宽 30 m,深 10 m。为了既能满座试验精度的要求,又能使模型更好的布置到水池中,模型缩尺取为 1:60。模型长 42 000 mm,宽 815 mm,高 1 860 mm。模型重 9 630 kg。模型的实际效果如图 1所示,主要参数见表 1。试验中 FDPSO 采用多点系泊,包括 16 根锚链线。锚链系统的布置见图 2,锚链线的主要参数见表 2。

|
图 1 FDPSO 模型 Fig. 1 The model of FDPSO |
|
|
表 1 FDPSO 主要设计参数 Tab.1 Main characteristic parameters of the FDPSO |
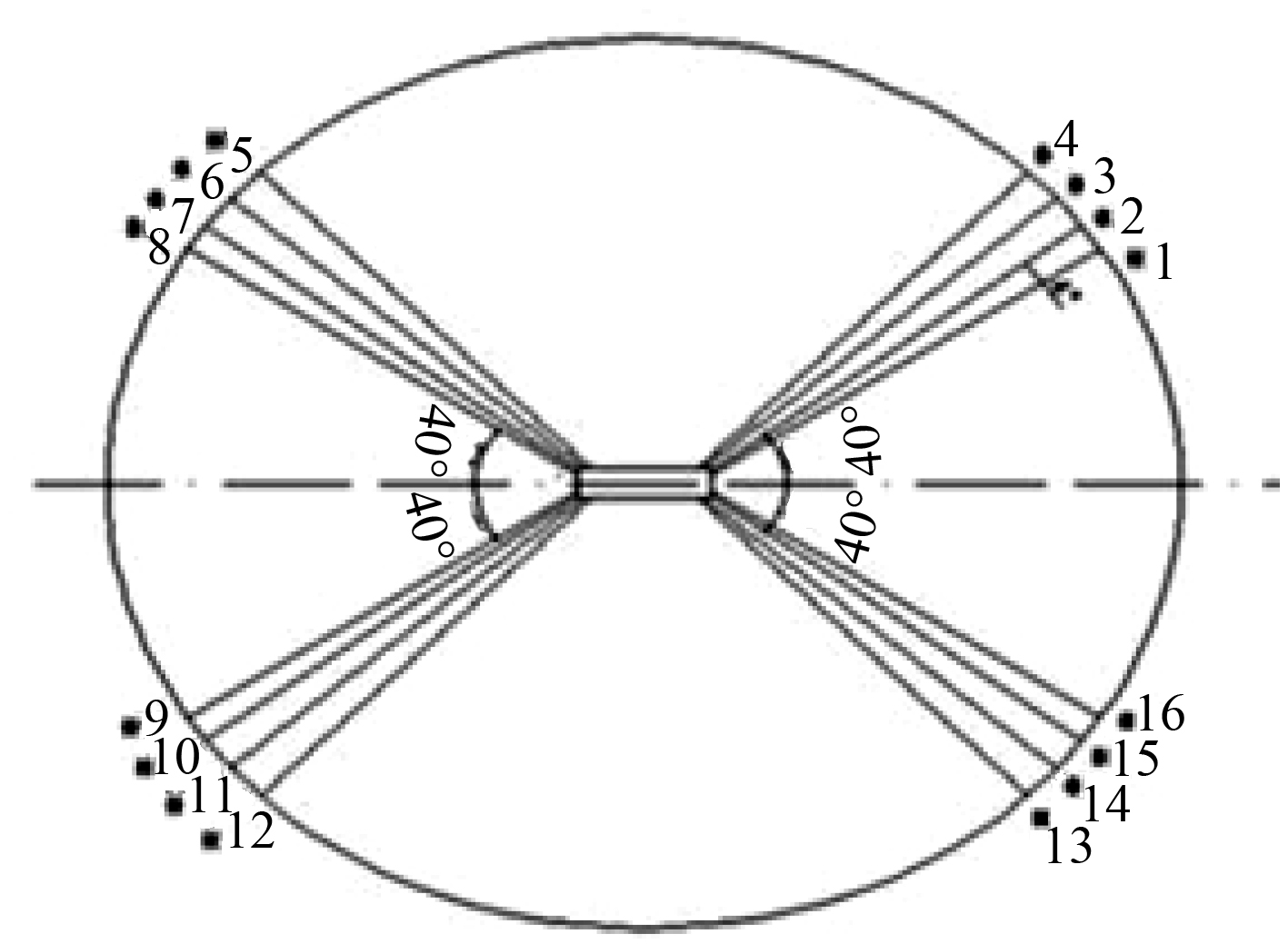
|
图 2 锚泊系统布置 Fig. 2 Arrangement of mooring system |
|
|
表 2 锚链线参数 Tab.2 Parameters of mooring lines |
在静水环境下进行了 FDPSO 系统的衰减试验,通过衰减时历曲线得到纵荡和横荡的无因此阻尼系数(见表 3)。
|
|
表 3 纵荡和横荡衰减 Tab.3 Surge and sway free decay results |
模型试验中采用的波浪参数见表 4,造波机通过 3 参数 JONSWAP 谱来制造时历不规则波。JONSWAP 谱公式为:
| $\begin{array}{l}S(\omega ) = 487[1 - 0.287\ln (\gamma )]\frac{{H_s^2}}{{T_p^4}}{\omega ^{ - 5}}\\ \cdot \exp \left( {\frac{{ - 1948}}{{T_p^4}}{\omega ^{ - 4}}} \right){\gamma ^{\exp \left[ {\frac{{ - {{(0.159\omega {T_p} - 1)}^2}}}{{2{\sigma ^2}}}} \right]} \text{。}} \end{array}$ | (15) |
式中:S(ω)为波浪谱能量分布;Hs 为有义波高;Tp 为谱峰周期,s ;γ 为谱峰值参数。
|
|
表 4 南海海浪谱参数 Tab.4 Wave parameters of the South Sea |
采用 AQWA-LINE 频域水动力计算模块计算该 FDPSO 的附加质量、辐射阻尼、一阶波浪力和二阶定长漂移力。在船体湿表面网格划分的过程中,为了使计算结果尽可能精确,而又不超过程序所允许的最大网格数(12 000 单元),文中采用最大网格边长不超过 1.0 m 的形式来控制网格的大小,水动力网格效果图如图 3所示。计算出该水动力模型的水动力参数及频域响应 RAO,在此基础上可利用时域耦合计算模块 AQWA-DRIFT 计算出 FDPSO 系统的时历响应结果。
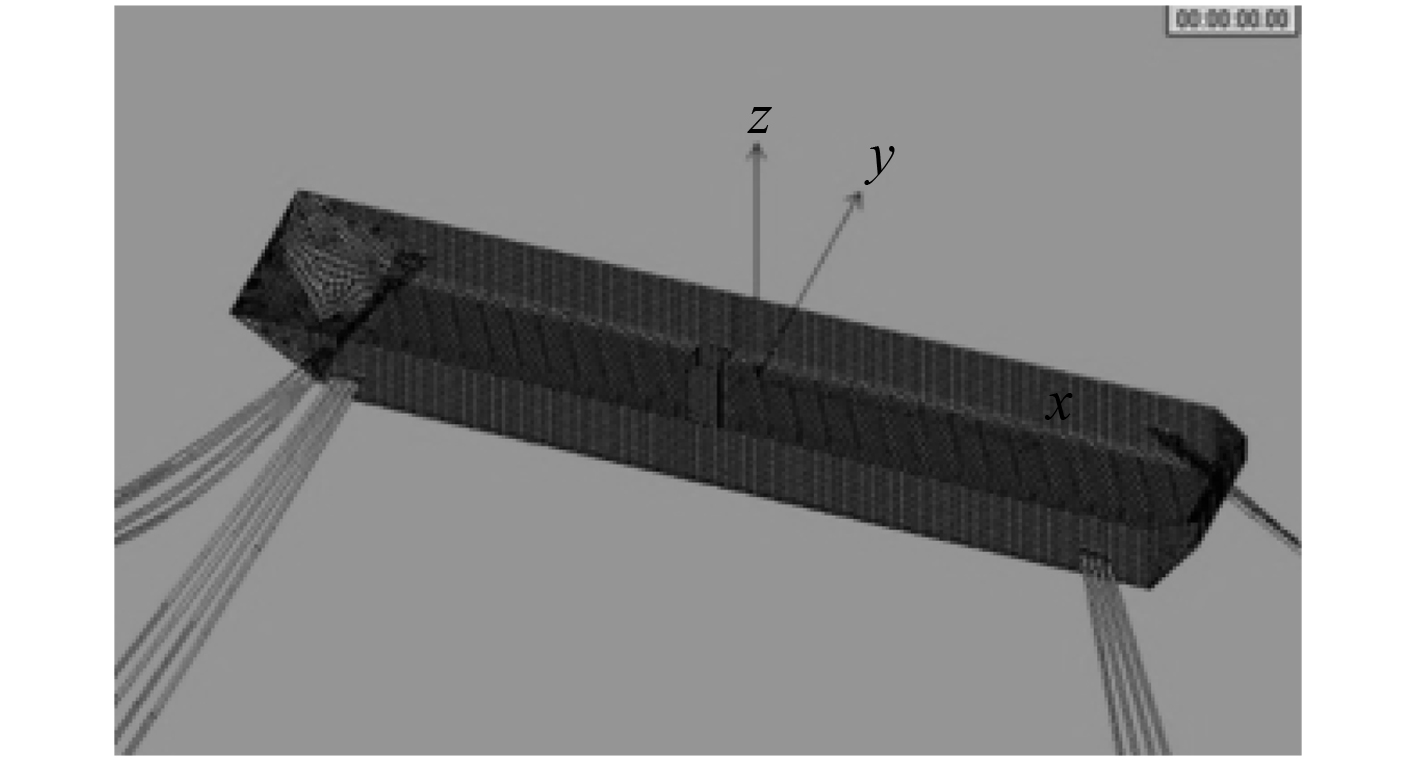
|
图 3 FDPSO 主船体水动力网格效果图 Fig. 3 Hydrodynamic model of FDPSO |
为了进一步验证该数值计算方法的精度和可靠性,本文将理论计算结果与试验结果进行对比。受到试验条件的限制,文中仅对比分析了 FDPSO 系统五自由度运动(缺少首摇)。在所选取的工况中,由于 13# 锚链线的张力变化最剧烈,因此在谈论中选取该锚链线作为研究对象,比较结果见表 5。通过表 5 中数据可以得出,理论计算结果与试验结果吻合的比较好,误差在可接受的范围内,从而验证了理论计算方法的可靠性。
|
|
表 5 理论计算结果与试验结果的对比 Tab.5 Comparison of the results between experiment prediction and numerical prediction |
文中采用南海百年一遇的海况对该 FDPSO 系统进行模拟,为了更好研究锚泊系统对 FDPSO 运动响应的影响,分别计算4种不同锚链预张力下 FDPSO 的运动响应。这4种不同的锚泊系统对应的预张力分别为 2 270,2 900,4 800 和 8 800 kN(为了描述方便,下文中采用 CaseⅠ,CaseⅡ,CaseⅢ 和 CaseⅣ表示)。通过数值模拟可以得到运动响应和锚链张力变化的时历信号,
数值计算结果见图 4 和表 6。通过图 4(a) 和4(b)可以得出不同的锚链预张力下 FDPSO 系统的纵荡和横荡运动响应结果相差较大,随着预张力的逐渐减小,运动响应的幅值和均值在不断变大。对于垂荡运动仅仅是均值发生了变化,这可以解释为锚链预张力的变化改变了初始状态下主船体的吃水。图 4(d) 显示了不同锚链预张力下横摇运动的周期不同,而运动的最大值最小值并未有明显的变化。
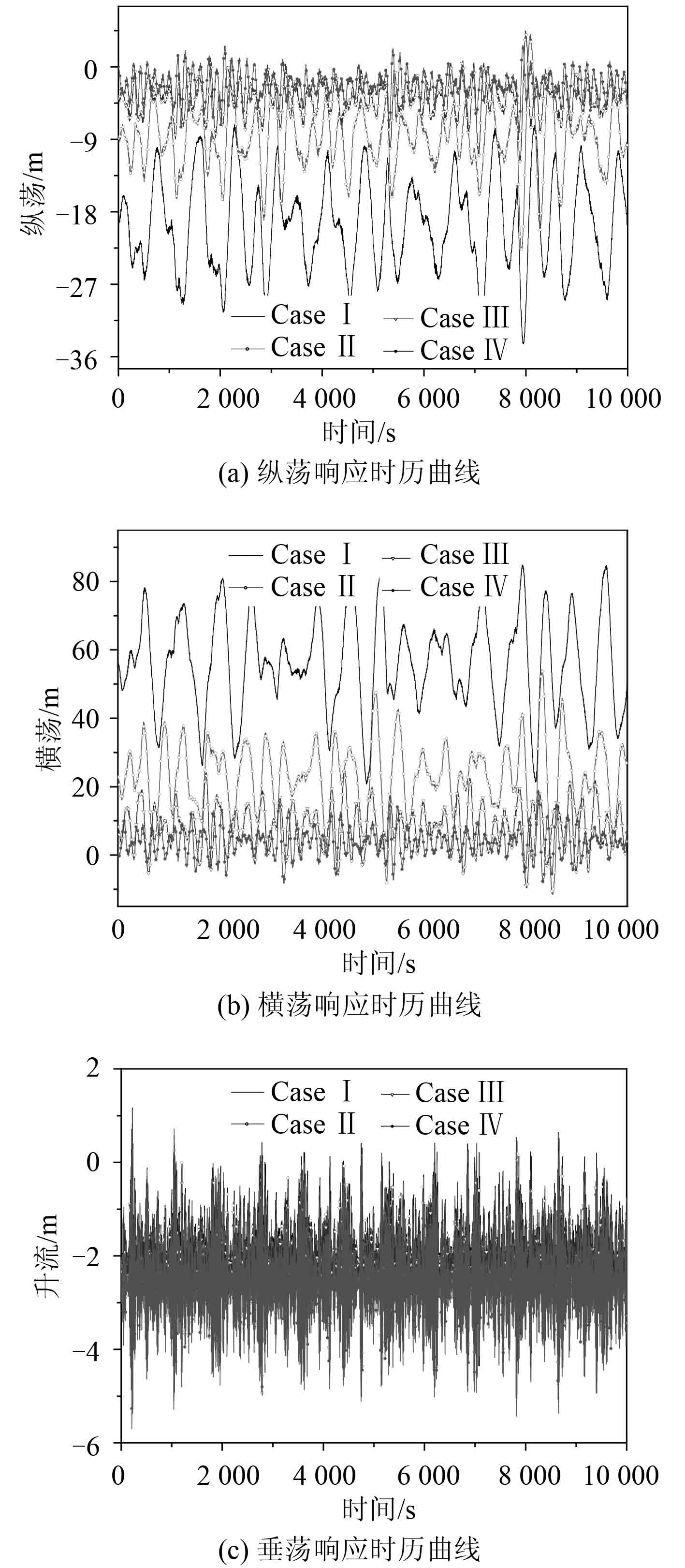
|
|
|
表 6 FDPSO 运动响应结果的对比 Tab.6 Comparison of FDPSO motion results |
为了进一步研究运动响应之间的区别,采用谱分析的方法对运动的时历信号进行傅里叶变化,求得运动响应谱。通常按照频率的高低,将运动响应谱划分为波频响应和低频响应[10]。从图 5 中不难得出,对于纵荡和横荡运动低频响应是主要的成分,而对于垂荡、横摇和纵摇,波频成分是主要的。随着锚链预张力的逐渐变小,纵荡和横荡响应谱的峰值逐渐变大(图 5(a) 和5(b)),这是由于纵荡和横荡运动的幅值会随预张力水平的下降而逐渐变大造成的(图 4(a) 和4(b))。结合图 4(a),4(b),5(a) 和5(b),不难得出锚链预张力对纵荡和横荡运动响应的影响较大。参照 API 规范[11]可知海上浮式采油平台的水平位移不得超过水深的 5%。为了满足这一要求,锚泊系统的预张力在设计之初就应被着重考虑。锚链预张力的变化对垂荡和纵摇响应的影响并不大(图 4(c),4(e),5(c) 和5(e))。从公式
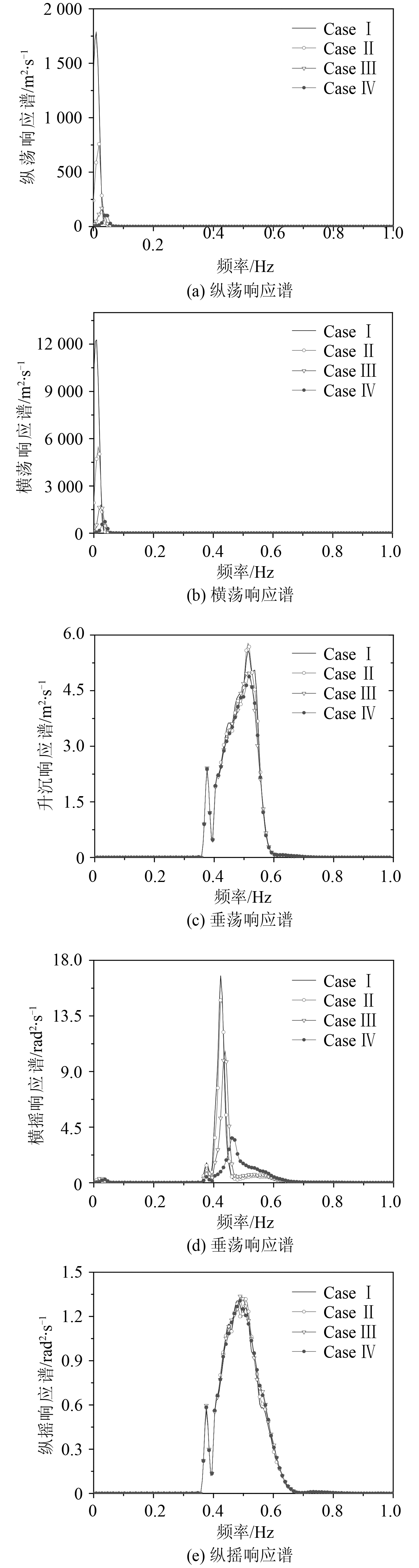
|
图 5 运动响应谱 Fig. 5 Spectrum of the motion |

|
图 6 FDPSO 的锚链力和合力(CaseⅢ) Fig. 6 Mooring force and total force of FDPSO (CaseⅢ) |
本文采用时域耦合计算方法对 FDPSO 系统的运动响应和锚链张力进行数值预报,并与试验结果进行对比验证了理论计算的可行性,在此基础上分别计算了不同预张力水平下的响应,通过对比分析计算结果得出以下结论:
1)低频运动是 FDPSO 系统纵荡和横荡运动的主要成分,随着锚链预张力的减小,纵荡和横荡运动响应的幅值会显著增大,在锚链系统的设计中应着重考虑。
2)对于垂荡、横摇和纵摇波频响应占主要部分,锚链预张力的变化对横摇运动的影响比较大而对垂荡和纵摇的影响比较小。随着预张力的增大,横摇运动响应谱的峰值周期逐渐变大。
| [1] | 苏志勇, 陈刚. 混合模型试验中截断系泊缆动力特性差异研究[D]. 上海: 上海交通大学, 2009. |
| [2] | SMITH, CHEN M C, RADWAN A M. " Systematic data for the preliminary design of mooring systems[J]”. Offshore Mechanics and Arctic Engineering Symposium, 1985[1]. |
| [3] | RADWAN, CHEN A M C, LEAVITT C W. " Design Curves for Chain Mooring Systems[J]”. Offshore Mechanics and Arctic Engineering Symposium, 1986(3). |
| [4] | XU Sheng, JI Chun-yan. " Dynamic of large-truncated mooring systems coupled with a catenary moored semi-submersible[J]”. China Ocean Engineering, 2014, 28(2), 149–162. |
| [5] | CHEN X H, MA J, W. " On dynamic coupling effects between a spar and its mooring lines[J]”. Ocean Engineering, 2001, 28: 863–887. |
| [6] | LUIS O G, MIACHAEL M B. " Analytical expressions of the bifurcation boundaries for symmetric spread mooring systems”. Appl Ocean Res, 1995, 17: 325–341. |
| [7] | MONTASIR O A, YENDURI A, KURIAN V J. " Effect of mooring line configurations on the dynamic responses of truss Spar platforms[J]”. Ocean Engineering, 2015, 96: 161–172. |
| [8] | 戴遗山, 段文洋. 船舶在波浪中运动的势流理论[M]. 北京: 国防工业出版社, 2008. |
| [9] | 刘应中, 缪国平. 船舶在波浪上的运动理论[M]. 上海: 上海交通大学出版社, 1987. |
| [10] | American Petroleum Institute (API). Design and Analysis of Stationkeeping Systems for Floating Structures. Recommended Practice 2SK, API-RP-2SK, 2005. |
| [11] | JI Chun-yan, YUAN Zhi-ming. " Study on a new mooring system integrating catenary with taut mooring”[J]. China Ocean Engineering, 2005, 25: 427–440. |
| [12] |
李焱, 唐友刚, 赵志娟. 新型多筒式FDPSO概念设计及其系泊系统分析[J]. 中国舰船研究, 2013(5).
LI Yan, TANG You-gang, ZHAO Zhi-juan. Concept design and analysis of the mooring system for the new type of multi-tubular FDPSO[J]. Chinese Journal of Ship Research, 2013(5). |
 2017, Vol. 39
2017, Vol. 39
