2. 高新船舶与深海开发装备协同创新中心,上海 200240;
3. 中国船舶及海洋工程设计研究院,上海 200011
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China;
3. Marine Design and Research Institute of China, Shanghai 200011, China
船体强度是研究船体结构安全性的科学。在进行船体强度有限元分析时,除了正确进行三维有限元模型的建模外,还要考虑正确的载荷施加方式和与之相匹配的应力衡准。通常,应力衡准需综合考虑船体梁应力和局部应力,在强度评估过程中可采用直接法或叠加法来得到相应的合成应力。随着计算机软硬件技术的发展,直接法在船体结构计算中得到了广泛应用,即在三维有限元模型中施加实际的局部载荷,同时准确模拟出船体梁弯矩或剪力。
现阶段船体强度评估过程中,船体承受的载荷主要包括空船质量、海水浮力、波浪载荷以及货物压力等。各载荷根据实船结构、装载情况和航行区域等条件确定。陈庆强等[1 –3]采用有限元方法对集装箱船等诸多船型进行了强度校核分析和相关技术的研究。其中船体梁载荷(弯矩或剪力)的施加方法不尽相同,郑雷[4]在进行 VLGC 全船结构有限元分析研究时,为保证三舱段分析中目标舱中间位置的弯矩值以及全船有限元分析中各个位置的弯矩值与设计弯矩一致,在船体结构各个肋位的甲板边线处施加集中力来实现弯矩调整;朱胜昌等[5]在大型集装箱船的总纵强度计算方法研究中,则直接将船体设计载荷施加于实肋位处左右对称分布的质量点上。
综合上述文献可发现,船体梁载荷的模拟通常在各剖面处施加集中力来实现。因此剖面集中力不同的加载方式将可能影响该剖面临近结构最终的应力和变形结果。如取剖面少数几个节点施加集中力的方法会导致局部产生较大的应力集中现象;如将剖面等效集中力平均分配到各网格节点上的做法则忽略了船体不同位置处构件受力的差异性。这些加载方式都会对船体结构的直接强度评估产生影响。本文根据薄壁结构力学理论提出基于剪流分布规律的节点力加载方式,并给出适用于计算机实施的规格化加载流程,实现了节点力的自动加载,以此获得更加准确的计算结果。
1 薄壁承弯构件的剪流分布 1.1 薄壁承弯构件的剪流分布规律船体结构主要由薄板构成,其长度远大于断面尺寸,船体本身可看成一个大型的、复杂的变断面薄壁杆件。薄壁杆件在受到弯曲作用时,薄壁断面会产生相应的弯曲剪应力来平衡邻近截面的弯曲正应力,可以认为剪应力的大小沿壁室厚度均匀分布,剪应力的方向沿薄壁的切线方向,将剪应力τ 和应力所处壁室厚度t 的乘积称之为剪流或者剪应力流f,即
| $f = \tau t{\text{,}}$ | (1) |
由力的平衡方程式可得薄壁杆件在平面内受到弯曲作用下的剪流计算公式:
| ${f_y} = \tau t = \frac{{{N_y}{S_x}}}{{{I_x}}}{\text{。}}$ | (2) |
式中:Ny 为该剖面上的剪力;Sx 为该剖面上长度s 的面积对x 轴的静矩;Ix 为该剖面对x 轴的惯性矩。
船体结构在受到弯曲作用时,截面的剪应力分布符合上述薄壁杆件剪流分布规律。
1.2 基于图论的薄壁承弯构件剪流计算船体结构剖面多连通,拓扑关系复杂,直接用薄壁杆件理论计算会遇到困难,结合现代组合数学利用图论作为工具,建立薄壁剖面的图模型,利用图论的定义、表达方式及若干重要结论即可求得船体结构剖面剪应力流分布[6]。
1.2.1 船体剖面图模型把船体剖面看成一个由若干顶点和边形成的线图,用 G (V,E)表示,其中V 为所有顶点的集合,E 为所有边的集合。顶点与边之间的关系可用关联矩阵 B 描述,并定义为:
| ${B}{\rm{ = (}}{{\rm{b}}_{ij}}{{\rm{)}}_{{N_v} \times {N_e}}},{b_{ij}} = \left\{ {\begin{array}{*{20}{c}}{ \ \ 1, {e_j} \in In{c^ + }({v_i}){\text{,}}}\\{ - 1, {e_j} \in In{c^ - }({v_i}){\text{,}}}\\{0, {\text{其他。}}}\end{array}} \right.$ | (3) |
式中:
基于船体剖面特性,船体剖面的图模型为连通图,所以连通图
G
的关联矩阵
B
的秩等于Nv
– 1。在
B
中划去对应于vk
顶点的行,则得到
当船体有双层底或为双舷侧结构时,船体结构剖面会形成闭室,闭室就形成了图模型中的基本回路。所有基本回路的集合用 C 表示,图中基本回路的个数用Nc 表示,定义为:
| ${C}{\rm{ = (}}{{\rm{c}}_{ij}}{{\rm{)}}_{{N_c} \times {N_e}}},{c_{ij}} = \left\{ {\begin{array}{*{20}{c}}{1, {e_j} \in Co{n^ + }({c_i}){\text{,}}}\\{ - 1, {e_j} \in Co{n^ - }({c_i}){\text{,}}}\\{0, {\text{其他}}\text{。}}\end{array}} \right.$ | (4) |
式中:
对于船体结构剖面可类比于电路网络,其中的剪流可类比于电流。
1)基于克希荷夫(Kirchhoff)电流定律:对于每一结点,流入该点的电流代数和为 0;在船体结构剖面图模型,对于每一个顶点,流入该点的剪流代数和为 0,即有:
| ${Bq} = 0{\text{。}}$ | (5) |
2)基于克希荷夫(Kirchhoff)回路定律:沿任一回路 C 电压降的代数和为 0;在船体结构受弯矩作用时,绕任一闭室一周剪切变形为 0,即有:
| ${C}\varGamma = 0{\text{。}}$ | (6) |
3)基于广义欧姆定律:运算电压等于运算阻抗与运算电流的乘积;根据剪切变形与剪应力之间的物理方程有:
| $\varGamma = q\frac{1}{{GT}}{\text{,}}$ | (7) |
上述求解方程中共有Ne 个未知数,有Nv +Nc 个方程,其中方程(6)中的Nv 个方程是线性相关的,任选一参考点可得到以下Nv – 1 个线性无关的方程:
| ${{B}_f}{q} = 0{\text{,}}$ | (8) |
联立方程(6)~ 方程(8),图论证明在连通图中存在下列关系[7]:
| ${N_v} + {N_c} - {N_e} = 1{\text{。}}$ | (9) |
求解出船体剖面各单元的剪流q。对于实际剖面,弧形边可用若干直线代替,不会引起显著误差[6]。
2 基于剪流分布规律的节点力加载方式目前,整船有限元分析的目的之一是进行总纵强度的直接计算。其载荷的处理通常有 2 种方法:一是把船体的外载荷和内载荷都施加到有限元模型上,在这些局部载荷的作用下有时仍需要施加剖面节点力以达到所要求的沿船长分布的船体梁设计弯矩或剪力;二是不考虑船体的外载荷和内载荷分布,只在各个剖面上构造相应的节点力以模拟沿船长分布的船体梁设计弯矩或剪力。
在船体舱段结构有限元分析中,当局部载荷在中间舱段引起的垂向和水平船体梁弯矩和剪力未达到船体梁载荷目标值时,需要在横向强框架位置处施加载荷予以调整。
整船有限元分析 2 种处理方式中在剖面上施加的作用力、舱段有限元分析过程中的剖面调整载荷均可通过基于剪流分布规律的节点力加载方式施加,即按剪流分布规律将等效集中载荷离散至各强框剖面处承剪构件的网格节点上。横向强框架取船体结构实肋位处以及横舱壁处;承剪构件即为船体纵向连续板,如舷侧外板、内壳纵舱壁、船底板、内底板、甲板及纵舱壁等。
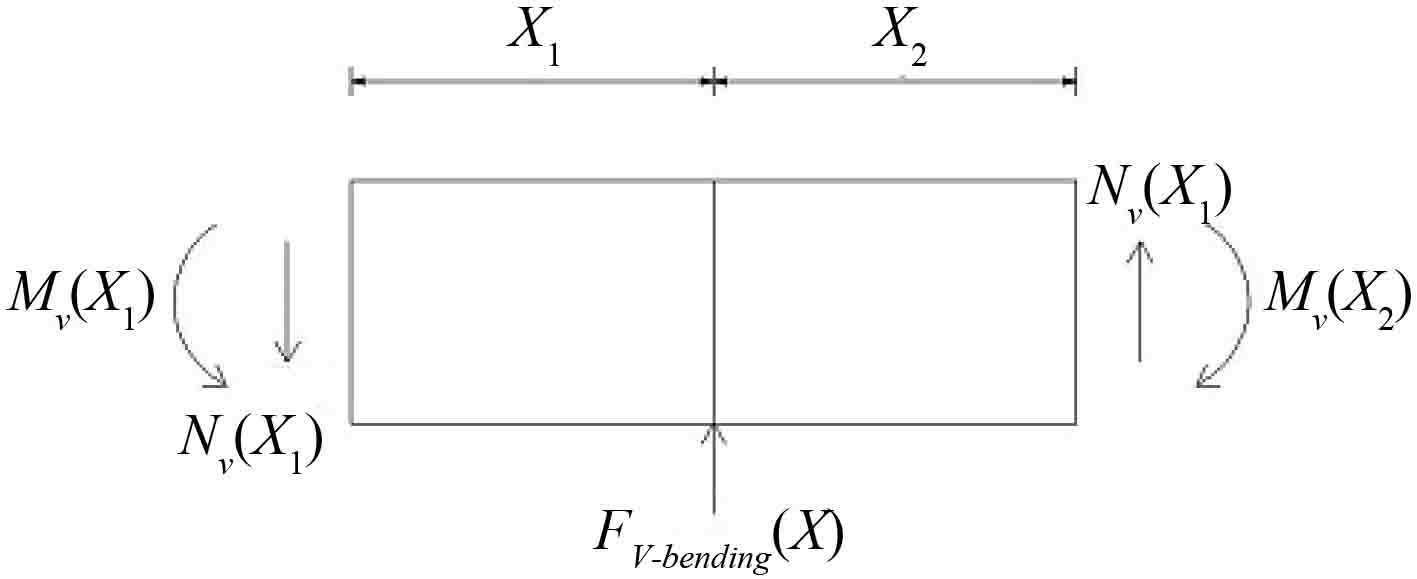
2.1 船体结构各强框剖面处的集中力将船体结构的垂向弯矩和水平弯矩分布曲线微分可得到对应的剪力分布曲线。以垂向弯矩为例,现假定船体梁承受的垂向总弯矩已经给定,船体结构中有m 个强框位置,包括横舱壁。为了确定各强框剖面位置处的垂向集中力
|
图 1 待定垂向集中力求解示意图 Fig. 1 Solution for concentrated vertical force |
| ${F_{V \!-\! \!bending\!}}\!\left( x \right)\! \!=\! {N_v}\!\left( {{x_1}} \right)\! - \!{N_v}\!\left( {{x_2}} \right)\! \!=\! \frac{{{\rm d}{M_V}\!\left(\! {{x_1}} \!\right)}}{{{\rm d}x}} \!-\! \frac{{{\rm d}{M_V}\!\left(\! {{x_2}}\! \right)}}{{{\rm d}x}}{\text{,}}$ | (10) |
其中MV 为沿船长分布的船体梁承受的垂向总弯矩(包括静水弯矩和波浪弯矩),kNm。
| ${x_1} = x - \frac{{{S_{aft}}}}{2}{\text{,}}{x_2} = x + \frac{{{S_{fore}}}}{2}{\text{。}}$ |
式中:Saft 为计算点所在强框与后 1 档相邻强框之间的纵向距离,m;Sfore 为计算点所在强框与前 1 档相邻强框之间的纵向距离,m;x 为计算点所在强框距离尾垂线的纵向距离,即纵向坐标,m。
依照上述类似方法,当单独考虑船体梁承受的水平总剪力时,依据其沿船长的分布可直接得到各强框剖面的集中力大小。如同时考虑船体梁承受的垂向总弯矩和总剪力,则在各个强框剖面位置处施加垂向集中力时需综合考虑并构造两类集中力,一类用于模拟垂向弯矩,一类用于模拟垂向剪力,同时在模型两端施加一附加弯矩(可通过在模型端部剖面内所有船体梁纵向有效抗弯单元上施加纵向轴向节点力来实现)予以平衡。
2.2 强框剖面处集中力的离散化各强框剖面处的集中力按照剪流分布规律,离散至船体结构承剪构件的节点上。以垂向集中力为例,船体结构某强框剖面处第k 个单元中点处的剪流为:
| ${q_{fv - k}} = \frac{{{F_{V - bending}}}}{{{I_y}}}{S_{kv}}{\text{,}}$ | (11) |
式中:Iy 为船体梁截面垂向剖面惯性矩,mm4;Skv 为第k 个单元绕水平中和轴的静矩,mm3。
求得剪流后,强框剖面处船体结构承剪构件中,第j 个单元网格节点处的分布剪力为:
| ${F_{j - grid}} = \mathop \sum \limits_{k = 1}^n {q_{fv - k}}\frac{{{l_k}}}{2}{\text{。}}$ | (12) |
式中:lk 为强框剖面上连接到节点j 的第k 个单元的长度,mm;n 为连接到节点j的船体梁承剪构件单元总数。
船体结构各强框剖面位置处的等效水平集中力可按类似方法离散至船体结构承剪构件的单元网格节点处,节点力大小利用船体梁剖面特性和剪流理论计算求得。
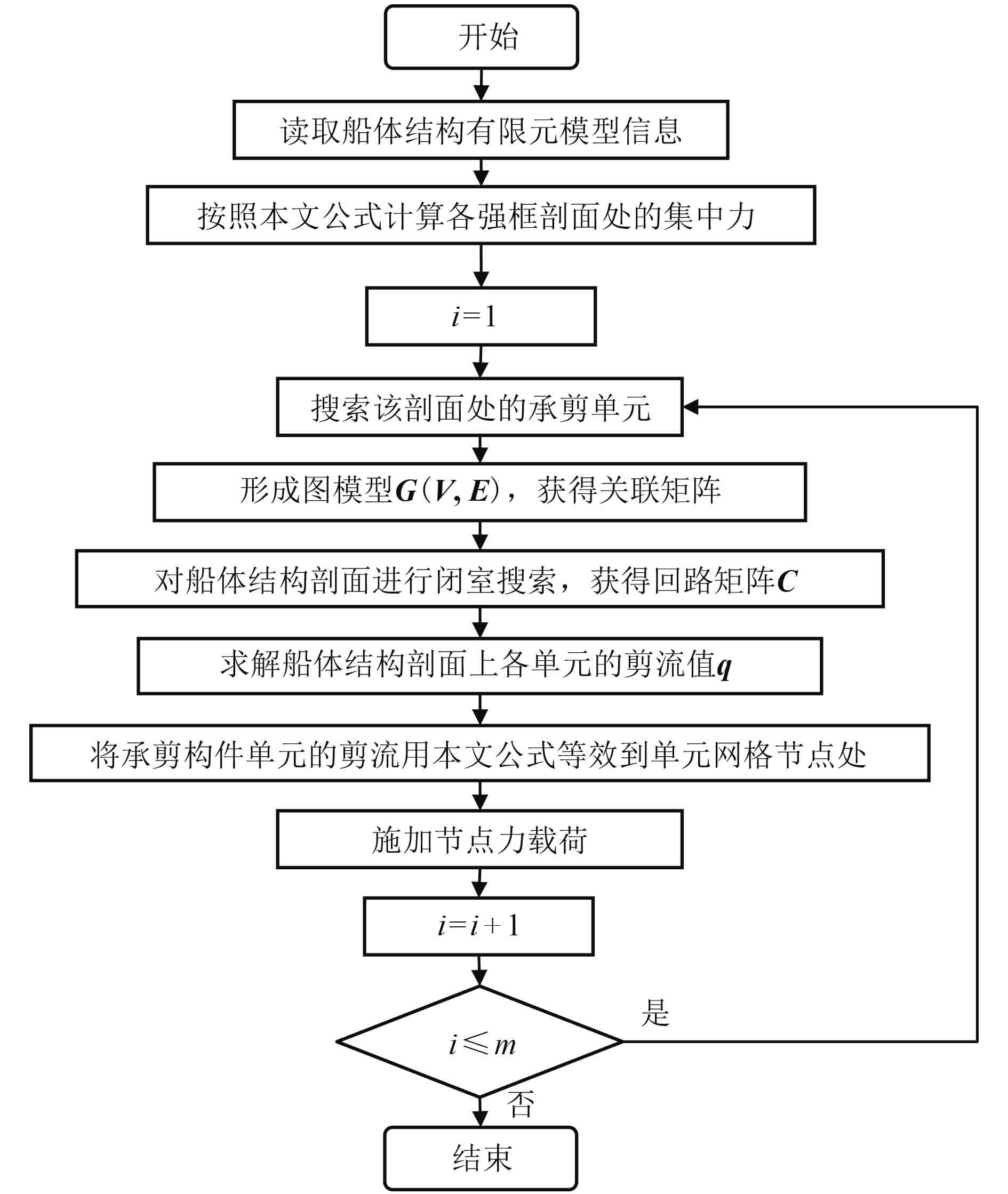
3 基于剪流分布规律的节点力自动加载程序及算例 3.1 基于剪流分布规律的节点力自动加载程序本文设计了基于剪流分布规律的节点力自动加载程序。该程序首先需设定强框剖面纵向位置(共m 道强框剖面)、船体结构承剪构件单元、船体梁载荷目标值等参数;然后按照有限元模型的空间关系找到加载的相关单元;用有限元模型的节点坐标值信息和单元节点关系信息构成船体强框剖面图形模型,用图论建立求解方程组,计算船体剖面各承力构件所分担的载荷值,最后等效至承力构件网格节点上进行加载。自动加载程序流程如图 2 所示。
|
图 2 基于剪流分布规律的节点力自动加载程序 Fig. 2 The automatic nodal force loading program based on the rule of shear flow distribution |
在自动加载程序中,为了找到某一横舱壁上的承剪构件,首先根据横舱壁的几何位置,在已获取的整船承剪构件中对所有单元长度方向的单元节点坐标值进行判别,继而获得与该横舱壁相关的承剪构件[9]。程序中为获取船体剖面闭室,采用至上而下对船体剖面进行扫描以获得所有节点事件点的方法。在船体剖面中,节点事件为该剖面上所有承剪构件的单元网格节点。依次查找所有事件点所围成的闭室[10],如果闭室存在则将与该闭室有关的结构单元记录到结果中,然后搜索下一个节点事件。
3.2 算例本文取 4250TEU 集装箱整船模型为例,有限元模型如图 3 所示。

|
图 3 4250TEU 集装箱船有限元模型 Fig. 3 The FEM model of 4250TEU container vessel |
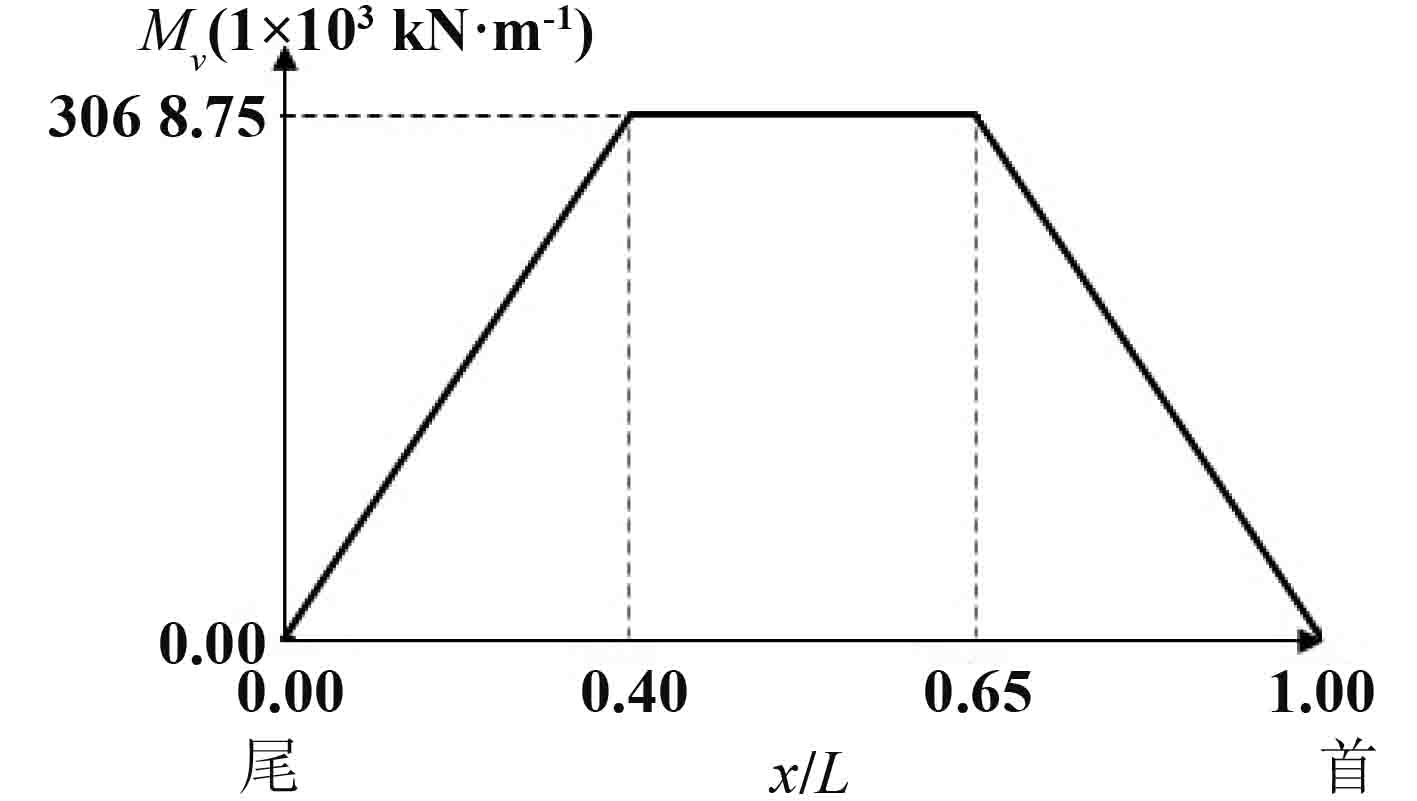
本文分别采用 3 种加载方法加载沿船长分布的垂向弯矩值MV ,弯矩分布如图 4 所示。
|
图 4 沿船长分布的垂向弯矩值Mv Fig. 4 The distribution of vertical bending momentMv |
根据本文公式将垂向弯矩转化为强剖面位置处的等效集中力。3 种节点力加载方式在船体结构横向强框剖面处的垂向集中力布置如表 1 所示。
|
|
表 1 强框剖面处垂向弯矩的等效集中力 Tab.1 The equivalent concentrated force of vertical bending moment at web frame sections in 3 difference ways |
对 3 种加载形式分别进行船体结构静力分析,边界条件设置如下:首垂线与底部外板的交点约束X,Y 和Z 方向的线位移;尾垂线与底部外板的交点约束Y 方向的线位移;尾垂线所在横剖面内,舷侧外板与干舷甲板的 2 个交点约束Z 方向的线位移[9]。
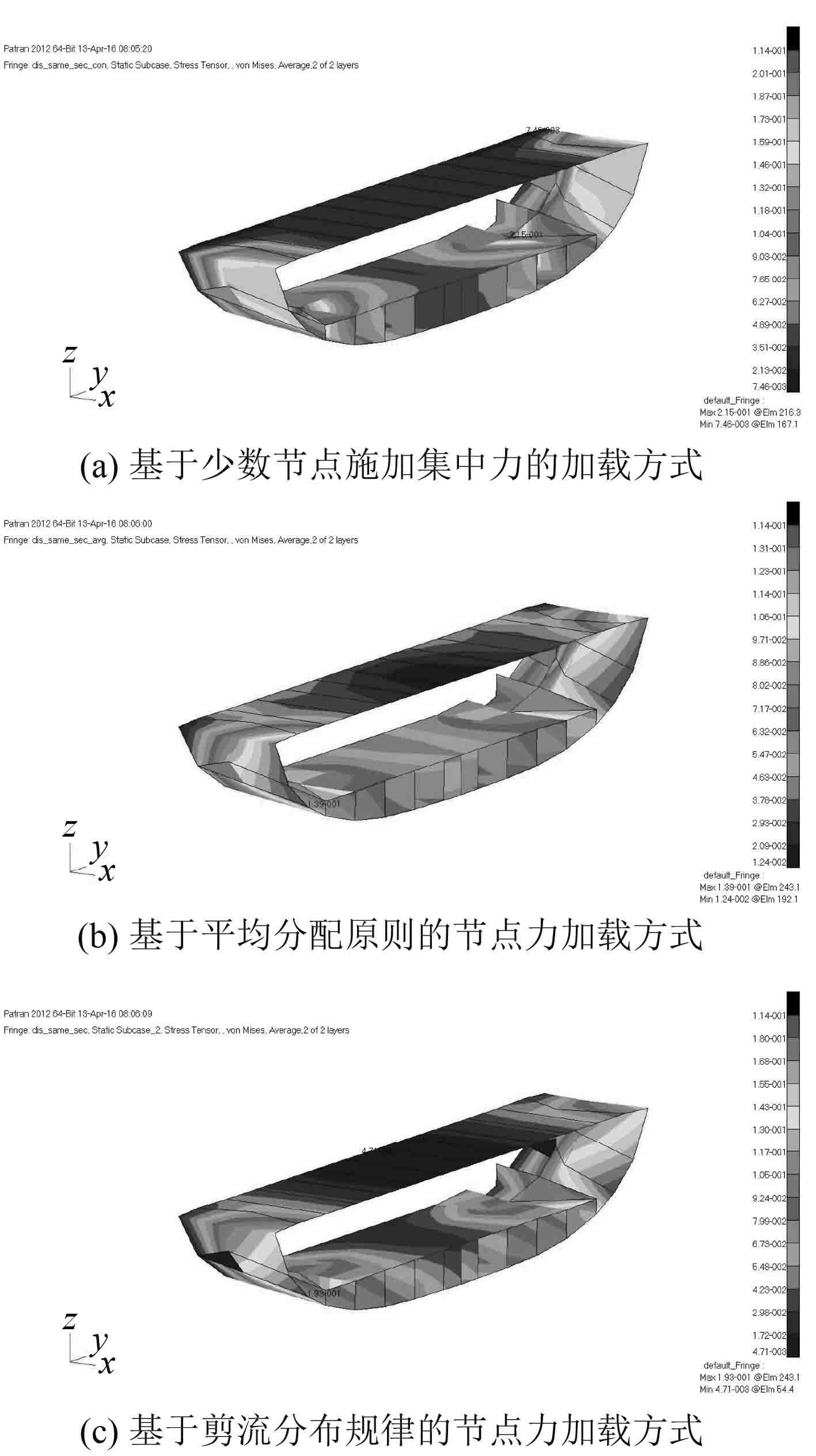
1)分析 3 种加载方式所得到的整体有限元模型 Von-Mises 应力云图如图 5 所示。不同的加载方式下船体结构的应力分布规律基本一致。目前大部分学者对基于少数节点施加集中力和基于平均分配原则的节点力加载方式都做了相应的计算研究(图 5(a) 和图 5(b)),因 3 种方式得到的船体结构应力、变形分布总体上一致,即本文提出基于剪流分布规律的节点力加载方式可行;

|
图 5 采用 3 种不同加载方式下的整船模型应力云图 Fig. 5 The stress contour of the whole ship FEM model under three different ways of loading |
2)3 种加载方式在施力剖面处的应力分布规律存在差异。
基于少数节点施加集中力的方法在施力节点附近(船尾外板与舵机舱平台交点)会产生应力集中现象。而基于平均分配原则的节点力加载方式和基于剪流分布规律的加载方式不会出现此类的现象(见图 6)。
|
图 6 采用 3 种不同加载方式下船艏模型应力云图 Fig. 6 The stress contour of the prow FEM model under three different ways of loading |
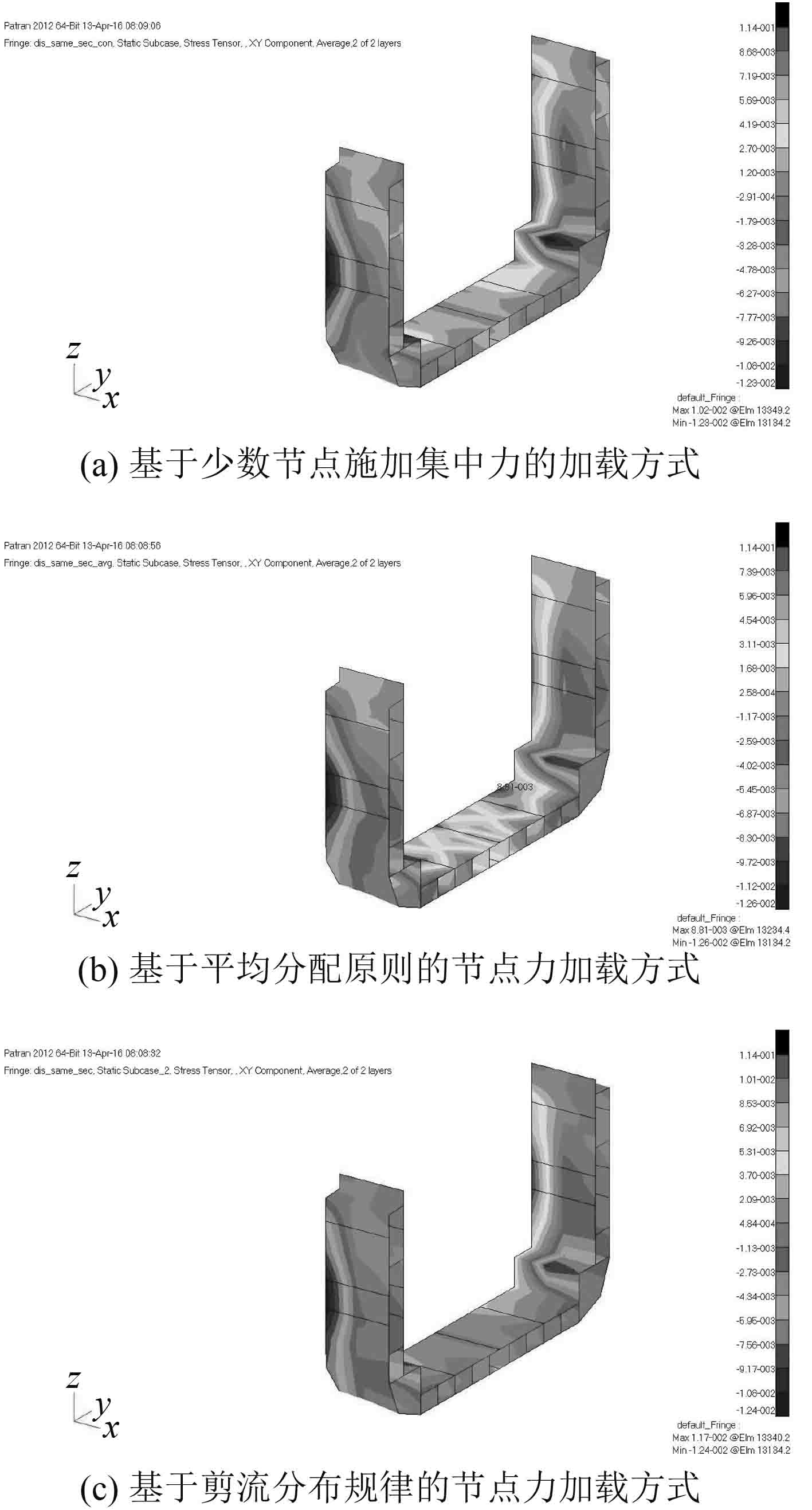
3 种加载方式在施力剖面及其附近区域上的剪应力分布存在差异。取典型施力强框剖面及其前后各一档强框范围内的模型(见图 7)。基于少数节点施加集中力的加载方式(图 7(a))和基于剪流分布规律的节点力加载方式(图 7(c))在船体两侧的剪应力较大,而船体结构底部对称轴附近的剪应力较小。而基于平均分配原则的节点力加载方式(图 7(b)),剪应力最大值仍出现在船体结构两侧的中和轴附近位置,但其底部的剪应力较另外 2 种方法的结果偏大。其原因在于基于平均分配原则的加载方式在图 8 中所示的底部节点上施加的节点力比基于剪流分布规律的加载方式施加的节点力大,其值如表 3 所示。基于少数节点施集中力的方法所取施力点远离船底对称位置,所以该方法对船底部对称轴附近的剪应力分布规律影响较小。依据船体梁受弯时剖面的剪应力分布规律可知,远离中和轴的船底对称位置处和剖面顶端舱口处的剪应力最小,向船体中和轴位置剪应力逐渐增大,由此得出基于少数节点施加集中力的加载方式和基于剪流分布规律的节点力加载方式产生的剪应力结果更准确。
|
图 7 典型强框剖面处的剪切应力云图 Fig. 7 The stress fringe of typical web frame section |
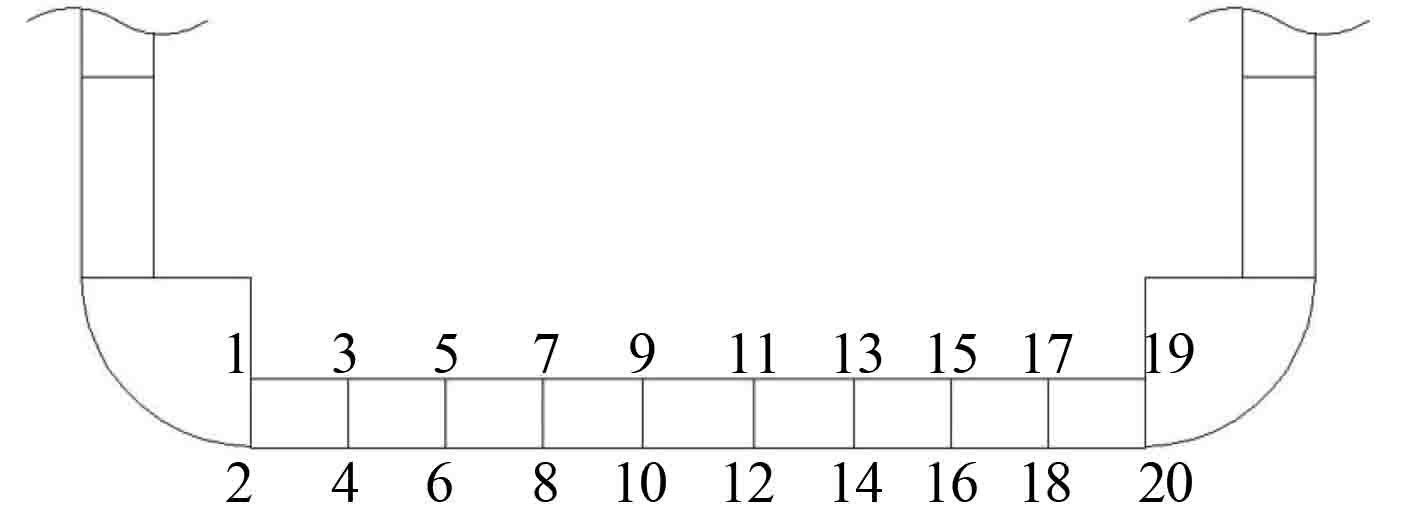
|
图 8 模型双层底部位的主要节点编号 Fig. 8 The serial number of key points at the model’s bottom |
|
|
表 2 模型双层底部位的主要节点处垂向分量载荷值(kN) Tab.2 The vertical component of load value at key points on the model’s bottom |
综合以上结果,基于剪流分布规律的节点力加载方式不会出现诸如选取少数节点加载剖面集中力而产生的明显应力集中现象,也消除了基于平均分配原则的加载方式带来的剪切应力分布与实际的差异,所得结果既满足船体梁载荷的模拟要求,同时也符合船体结构弯曲时的剪切应力分布规律,在船体结构有限元分析中可获得更加准确的结果。
4 结 语1)本文总结了船体结构有限元分析中弯矩和剪力的加载方式,提出了按照剪流分布规律的节点力加载方式,并用算例对比分析了 3 种不同加载方式所产生的结果,得出基于剪流分布规律的加载方式在保证准确模拟船体梁载荷的前提下更符合船体结构弯曲时的剪切应力分布规律,对于正确地进行船体结构强度有限元分析具有指导性作用。
2)本文给出的方法适用于计算机实施的规格化过程,根据本方法编制的程序在实际的船体结构有限元模型上得到了验证。通过程序自动加载过程省去了加载时间,提高了船体有限元分析的效率。
| [1] |
陈庆强, 朱胜昌. 大型集装箱船整船有限元分析计算技术研究[J]. 船舶力学, 2006, 10(1): 80–91.
CHEN Qing-qiang, ZHU Sheng-chang. Research on numerical technique of whole large container ship by FEM [J]. Journal of Ship Mechanics, 2006, 10(1): 80–91. |
| [2] |
韩钰, 陈磊, 王伟飞, 等. 超大型集装箱船的结构设计[J]. 船舶与海洋工程, 2015, 31(4): 10–17.
HAN Yu, CHEN Lei, WANG Wei-fei, et al. The structural design of ultra large container ships [J]. Naval Architecture and Ocean Engineering, 2015, 31(4): 10–17. |
| [3] |
罗秋明, 薛鸿祥, 唐文勇. 45万吨级超大型矿砂船全船结构有限元分析[J]. 船舶工程, 2010, 32(2): 8–12.
LUO Qiu-ming, XUE Hong-xiang, TANG Wen-yong. Finite element analysis of ship structure of 450000DWT Ultra-Large ore carrier[J]. Ship Engineering, 2010, 32(2): 8–12. |
| [4] |
郑雷, 李小灵, 王亮. VLGC全船结构有限元分析研究[J]. 船舶工程, 2015, 37(1): 28–31.
ZHANG Lei, LI Xiao-ling, WANG Liang. FE analysis of global structure of very large gas carrier [J]. Ship Engineering, 2015, 37(1): 28–31. |
| [5] |
朱胜昌, 陈庆强, 江南. 大型集装箱船总纵强度计算方法研究[J]. 船舶力学, 2001, 5(2): 34–42.
ZHU Sheng-chang, CHEN Qing-qiang, JIANG Nan. Research on the calculating method of longitudinal strength of large container ship[J]. Journal of Ship Mechanics, 2001, 5(2): 34–42. |
| [6] |
胡毓仁. 图论在薄壁杆件构件计算中的应用[J]. 上海交通大学学报, 1989, 23(6): 21–29.
HU Yu-ren. The application of graph theory to structural calculation of thin-walled Bars[J]. Journal of Shanghai Jiaotong University, 1989, 23(6): 21–29. |
| [7] |
卢开澄, 卢华明. 图论及其应用(第二版)[M]. 北京: 清华大学出版社, 1995.
LU Kai-cheng, LU Hua-ming. Graph theory and its applications(2版) [M]. Beingjing: Tsinghua University Press, 1995. |
| [8] |
李敏, 张世联. 基于PCL语言的船体剖面特性计算[J]. 舰船科学技术, 2014, 36(10): 27–31.
LI Min, ZHANG Shi-lian. Calculation of hull section characteristics based on PCL [J]. Ship Science and Technology, 2014, 36(10): 27–31. |
| [9] | DANIEL Y C. A graphic-algebraic computation of elementary siphons of BS3PR[J]. Journal of Information Science and Engineering, 2007, 23: 1817–1831. |
 2017, Vol. 39
2017, Vol. 39

 强框剖面上所有承剪构件的网格节点
强框剖面上所有承剪构件的网格节点
 强框剖面上舷侧与甲板、
底边舱的交点
强框剖面上舷侧与甲板、
底边舱的交点