2. 中国船舶科学研究中心,江苏 无锡 214082
2. Chinese Ship Scientific Research Center, Wuxi 214082, China
近年来,国家致力于推动海洋工程装备突破发展,而深海潜水器是大洋勘查与深海科学研究的重要海洋工程装备。作为潜水器的重要组成部分,在下潜过程中,耐压壳起着保障内部设备正常工作和人员健康安全的作用,其重量占潜水器总重的 1/4~1/2[1]。
现有的球形耐压壳的设计与分析基于薄壳理论,并被各国船级社规范认同[2]。王自力等[3]认为,随着水深增加,耐压壳分析从薄壳(R/t < 6)问题转化为中厚壳(6 ≤R/t ≤ 20)或厚壳(R/t > 20)问题,现有的潜水器规范不适用于深海耐压壳分析,而对于厚球壳可直接根据有限元计算确定其极限强度。张建等[1]分别从理论和数值对球形耐压壳薄壳力学模型、厚壳力学模型进行了强度与稳定性特性分析,指出强度是厚球壳设计的主要影响因素,建议以内表面应力为基准设计和评估深海球形耐压壳。俞铭华等[4]对比分析了开孔耐压球壳与完整球壳的极限强度,表明有围壁加强的开孔耐压球壳与完整耐压球壳的极限强度相差不大。然而在深海环境中,耐压壳所处的工况复杂,比如水流的流动等不利因素都会影响耐压壳所承受的载荷的大小,因此在设计耐压壳的问题上不仅要考虑强度问题,也要分析疲劳损伤问题。
为此,本文分别从开孔加强耐压球壳和完整球壳 2 种模型研究球形耐压壳的强度、稳定性、疲劳损伤等性能。在 7 km 水深条件下,分别按开孔球壳模型和完整球壳模型,分析和对比壳体的强度、稳定性特性,并分析疲劳损伤值及使用寿命的差异。
1 完整球形耐压壳的强度和平稳性分析 1.1 理论分析随着水深的增加,耐压壳分析从薄壳问题转化为中厚壳问题,其中包括强度计算和稳定性的计算。厚壳内表面应力σin 如式(1),根据薄壳强度理论,球形耐压壳应力计算为如下:
| $\mathop \sigma \nolimits_{in} = \frac{{3p\mathop {(2 + \frac{t}{R})}\nolimits^3 }}{{2[\mathop {(2 + \frac{t}{R})}\nolimits^3 - \mathop {(2 - \frac{t}{R})}\nolimits^3 ]}}{\text{,}}$ | (1) |
| $\sigma = \frac{P}{{2\frac{t}{R}}}{\text{,}}$ | (2) |
则使用薄壳强度理论计算中厚壳表面应力的误差为:
| $\mathop \Delta \nolimits_\sigma = \frac{{\left| {\mathop \sigma \nolimits_{in} - \left. \sigma \right|} \right.}}{{\mathop \sigma \nolimits_{in} }} \times 100\% {\text{。}}$ | (3) |
深水球形耐压壳屈曲临界载荷[7]采用式(3)表达,该公式采用勒让德函数求解球形壳屈曲控制方程[8],推导出厚球壳稳定性问题的解析解为:
| $\mathop P\nolimits_{cr1} = \frac{{2Et}}{{R(1 - \mathop \mu \nolimits^{\rm{2}} )}}\left( {\sqrt {\frac{{({\rm{1 - }}\mathop \mu \nolimits^{\rm{2}} )}}{{\rm{3}}}} \frac{t}{R} - \frac{{\mu \mathop t\nolimits^2 }}{{2\mathop R\nolimits^2 }}} \right){\text{,}}$ | (4) |
Zolly 公式[6]是船级社球形耐压壳稳定性设计规范的共性理论基础,此公式基于薄壳理论。则薄壳稳定性问题的解析解为:
| $\mathop P\nolimits_{cr2} = \frac{{2E\mathop t\nolimits^2 }}{{\mathop R\nolimits^2 }}\sqrt {\frac{1}{{3(1 - \mathop \mu \nolimits^2 )}}} {\text{,}}$ | (5) |
则使用经典 Zolly 公式计算中厚壳屈曲临界载荷的误差 ∆ 为:
| $\Delta = \frac{{\left| {{P_{cr1}} - \mathop P\nolimits_{cr2} } \right|}}{{\mathop P\nolimits_{cr1} }} \times 100\% {\text{。}}$ | (6) |
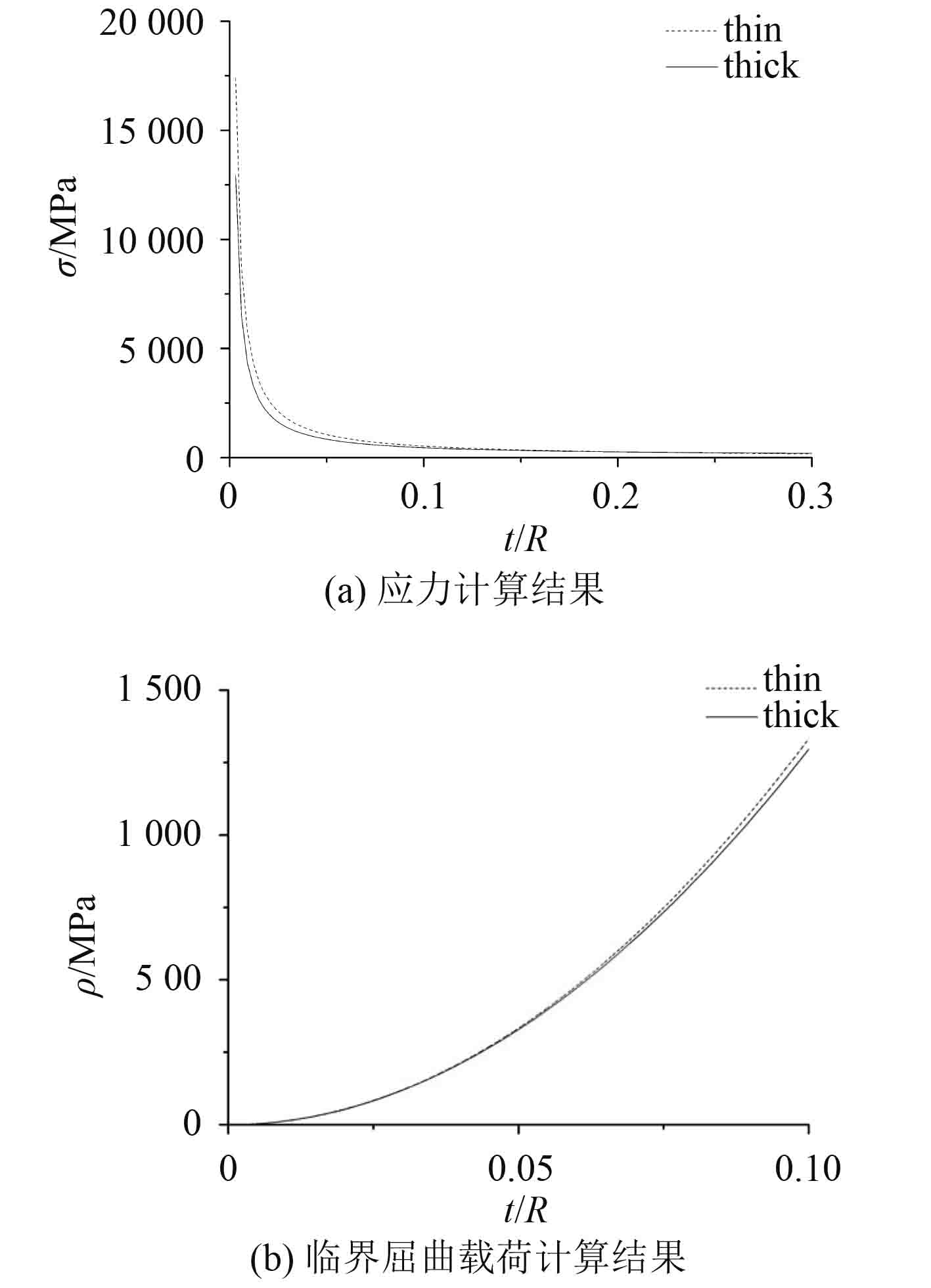
由图 1(a)可知基于薄壳理论的应力计算比厚壳计算值偏大,因此在评估中厚壳的强度时,可以使用厚壳理论计算公式。图 1(b)可知经典 Zolly 公式所得出的屈曲临界载荷偏于保守,比厚球壳屈曲临界载荷公式计算所得值偏大。因此,Zolly 公式在计算中厚壳的临界屈曲载荷时,可对中厚壳的稳定性进行初步的估计。
|
图 1 薄壳、中厚壳力学模型计算结果 Fig. 1 The calculation results of mechanical model of thin thick shell and Medium thick shell |
在深海环境中,如果耐压球壳的直径过大,会使潜水器过于钝粗,因此直径一般不会超过 2.5 m。为了简便,本文所研究的对象是直径 2 m 的球壳。假设球形耐压壳的材料选为 Ti-6AL-4V(TC4),得到计算载荷为:
| $\mathop p\nolimits_s = k\mathop \rho \nolimits_\omega gh/0.9{\text{,}}$ | (7) |
式中:k 为安全系数;ρω 为海水密度;g 为重力加速度;h 为海水深度。这里k 取为 1.35,ρω = 1.025 g/cm3,g = 9.8 m/s2,h = 7 km
计算得出,在 7 km 水深中球壳的计算载荷为 105.47 MPa,则球壳的厚度为:
| $t = \frac{{\mathop { P}\nolimits_s \times R}}{{2\mathop \sigma \nolimits_\phi }}{\text{。}}$ | (8) |
式中:R 为球壳的半径;σφ 为中面应力,σφ = 830 MPa。
计算得出球壳的厚度为 63 mm,即符合规范[2]中t 不得小于 15 mm 的要求。
球壳模型半径R 与壳体厚度t 之比为 15.87,属于中厚壳结构[3]。网格划分采用网球划分方式,并采用高精度 20 节点 solid186 体单元。耐压球壳在水下工作时所受载荷为压载荷且大小均匀,不受任何约束,而结构刚体位移在有限元位移法计算中是不允许的,故计算模型需有一定的位移约束。因此可将约束形式定为:z 轴上取两节点限制沿x,y 轴的位移(ux = 0,uy = 0),和这 2 点同一经度上相隔 90° 的位置取第 3 个约束节点,限制沿x,z 方向上的位移(ux = 0,uz = 0)[4]。
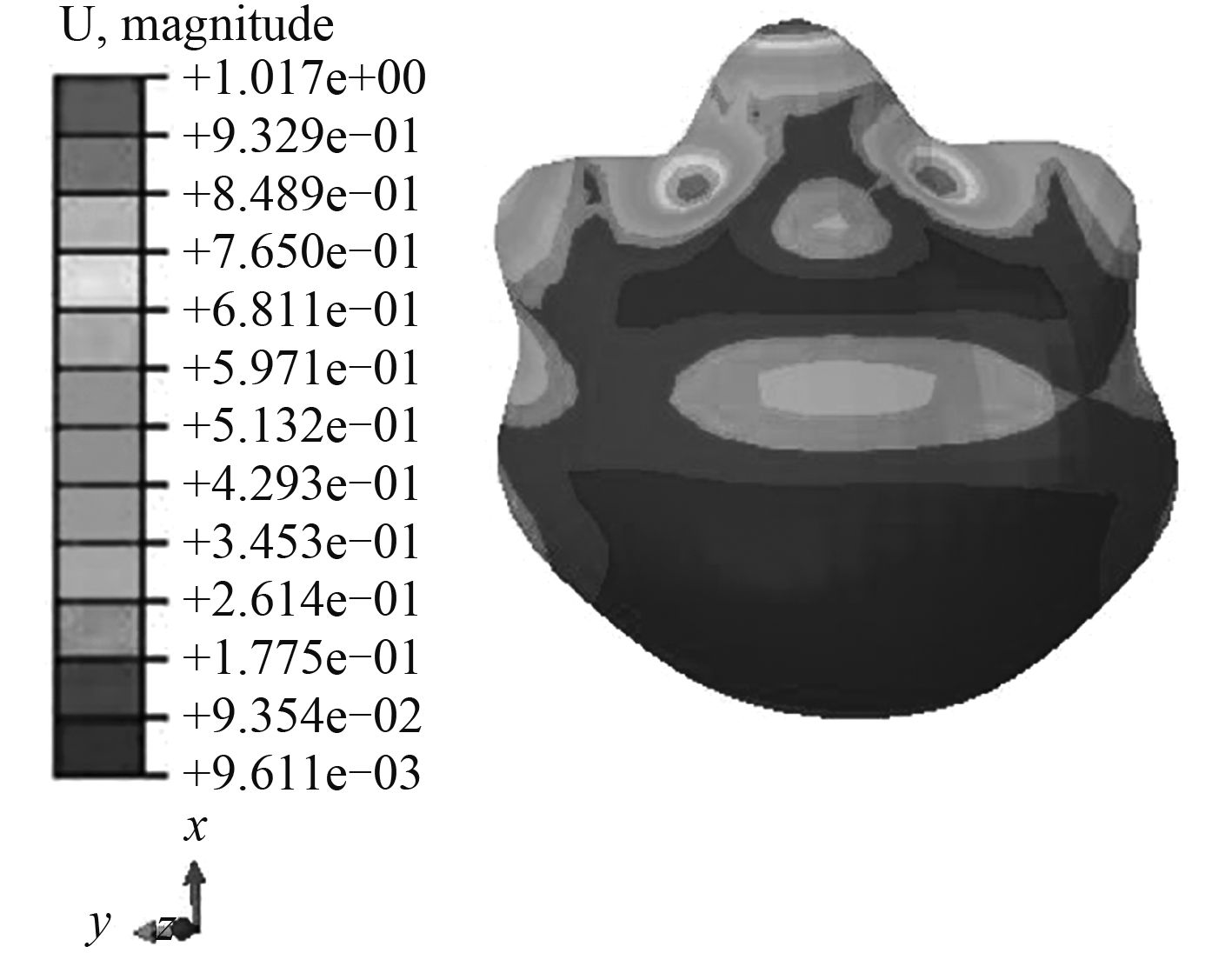
1.3 完整球形耐压壳有限元分析深海水深为 7 km,此时球壳所承受的载荷为 78.1 MPa,无开孔完整球形耐压壳的极限承载力为 124.55 MPa[3],因此理论计算的承载力符合要求。图 2 表示球壳在深海中的应力云图,其最大值为 717.1 MPa,最小值为 581.6 MPa。球壳的材料选为钛合金,屈服强度为 830 MPa,材料极限应力为 960 MPa,由应力云图可以得知,完整球壳在深海工作过程中材料强度满足要求。图 2 表明球壳所受的应力在径向方向上,从外表面到内表面应力逐渐增大,最大应力出现在球壳内表面,最小应力出现在球壳外表面。图 3 是完整球壳屈曲分析结果,一阶屈曲特征值为 7.57。屈曲分析时,对完整球壳所加的载荷为 78.1 MPa,根据第一阶屈曲特征值可以得出压力在 591.2 MPa 时,球壳才会出现失稳状态。因此可以得出在 7 km 水深中,材料的强度是耐压壳失效的主要影响因素。

|
图 2 完整球壳静力学分析结果 Fig. 2 Results of static analysis of complete spherical shell |
|
图 3 完整球壳屈曲分析结果 Fig. 3 Results of buckling analysis of complete spherical shells |
为了确定有限元计算结果的合理性,将理论模型的计算值与完整球壳有限元计算结果进行对比分析,具体比较如表 1 所示。结果表明二者计算结果相差不大。
|
|
表 1 完整球壳有限元分析结果与理论计算对比分析 Tab.1 Comparison between finite element analysis results and theoretical calculation of full spherical shell |
潜水器都必须有多个开孔,它们用于人员的出入口,观察窗口以及一些贯穿孔。倘若这些孔的尺寸较大就会对球壳的强度产生影响,因此需要对开孔附近部分进行加强。为了研究的方便,本文仅对球壳开一个人孔,并根据中国船级社颁布的潜水系统和潜水器入级与建造规范[2]对球壳进行围壁加强设计。
根据船级社规范,对球壳围壁尺寸进行计算,开孔耐压球壳的设计参数如表 2 所示,开孔球壳围壁加强示意图如图 4 所示。
|
|
表 2 开孔球形耐压壳设计参数 Tab.2 Design parameters of pressure spherical shell with opening |

|
图 4 开孔球壳围壁加强示意图 Fig. 4 Schematic diagram of the enclosure wall of the opening spherical shell |
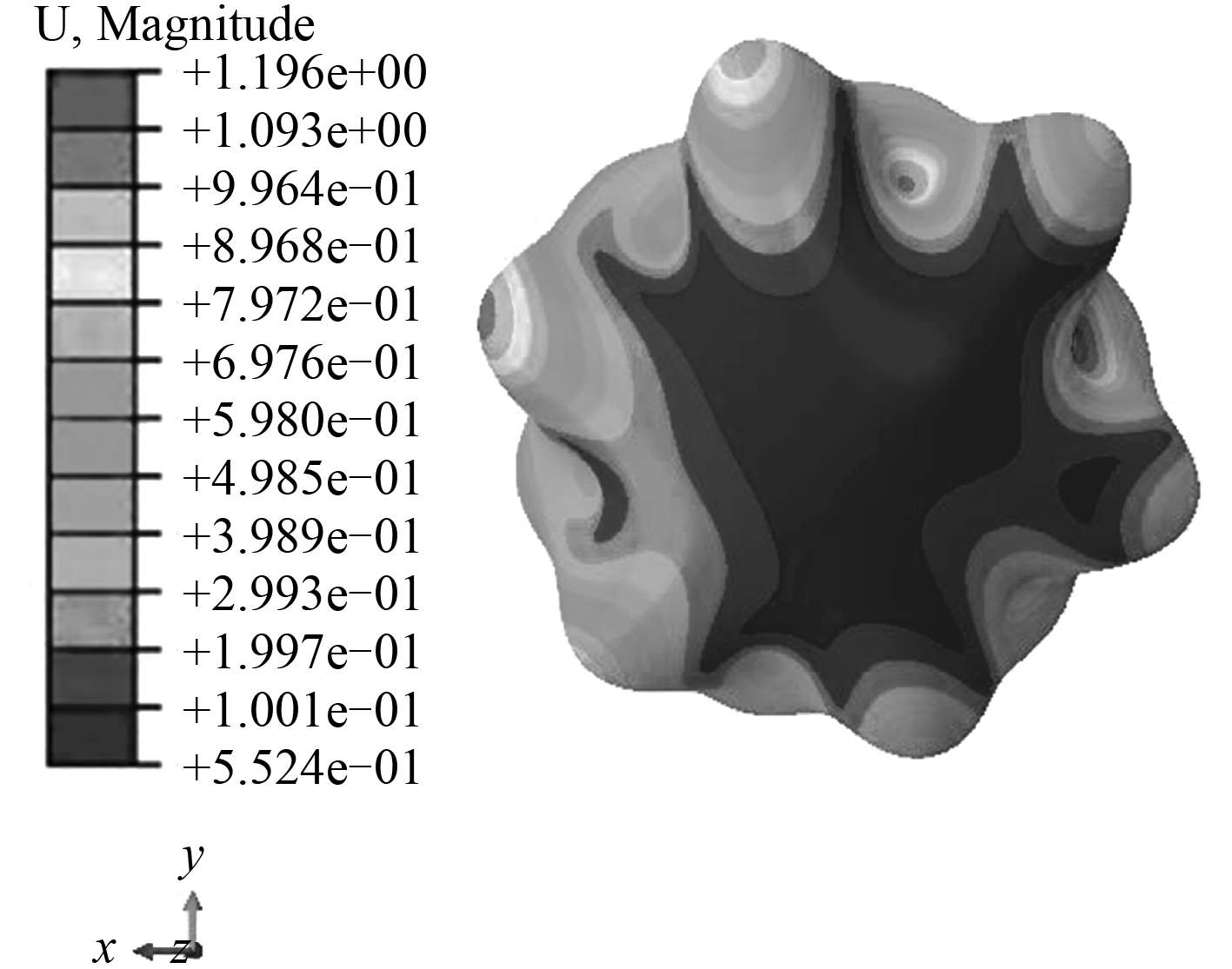
根据船级社规范,对开孔球形耐压壳进行围壁加强。为了验证围壁加强的球壳与完整球壳强度的相似性,同样对其进行静力学分析及屈曲分析。从图 5 中可以看出围壁加强的球壳在 7 km 海深条件下工作时,最大应力为 792 MPa。分析结果表明开孔加强后的球形耐压壳与完整球形耐压壳强度相差不大。图 6 是屈曲分析的结果,其一阶屈曲特征值为 6.12,屈曲分析时与完整球壳一样所加载荷为 78.1 MPa,根据第一阶屈曲特征值可以得出压力在 478.2 MPa 时,圆形开孔加强耐压球壳会出现失稳状态。同样印证了在 7 km 水深中,材料的强度是失效的主要影响因素这个结论。

|
图 5 开孔加强球壳静力学分析结果 Fig. 5 The static analysis results of strengthened spherical shell with opening |
|
图 6 开孔加强球壳屈曲分析结果 Fig. 6 The results of buckling analysis of strengthened spherical shell with opening |
为了研究开孔加强形式对耐压球壳强度、屈曲失稳压力的影响、将单开孔跟无开孔耐压球壳的计算结果进行对比,结果如表 3 所示。
|
|
表 3 完整球壳与开孔加强球壳分析对比 Tab.3 Analysis and comparison of complete spherical shell and strengthened spherical shell with opening |
数值法与试验法的结合已成为研究深海耐压器的有效方法,本文为了验证上述的数值结果,按照 1:10 的比例制作了不锈钢缩比试验模型,试验模型如图 7 所示。为了模拟深海环境,实验设备选用本课题组自主研发的水压环境模拟试验台,试验台通过 PLC 无级调节压力舱内的水压,可获得准确的破坏压力与失效模型。通过水压试验获得的开孔加强球壳的失效模式,如图 8 所示。从图中可见,球壳的失效位置在围壁与球体的结合处,这一结果与有限元分析结果一致。理论计算围壁加强球壳遭到破坏时所需载荷为 22.1 MPa,在实验中,实验模型破坏时,压力表显示的数值为 20.5 MPa,则理论计算值与实验数据相差 7.2%,二者的差值在实验误差范围之内。产生误差的原因可能是围壁与球体的结合处为焊接焊缝,且此处结构的突变容易造成应力集中,这 2 个因素影响了开孔球形耐压壳的强度及稳定性。

|
图 7 试验模型 Fig. 7 Test model |

|
图 8 试验结果 Fig. 8 Test result |
由于耐压球壳在 7 km 深海工作,材料的疲劳强度是失效的主要影响因素,故对其进行疲劳分析。完整球壳的材料采用 TC4,屈服强度为 830 MPa,根据静力学分析结果可知,最大应力为 717.1 MPa,所以球壳发生弹性变形。本文所建立的球壳模型在深海中工作时,忽略水流的流动,温度等因素对球壳所受载荷的影响。假设在 7 km 水深中,球壳所受载荷不变,因此球壳会产生疲劳损伤的过程是从水平面潜到水深为 7 km的指定作业位置,在这个过程中,球壳受到变载荷的作用,从而产生疲劳损伤。使用 FEMFAT 软件对完整球壳进行疲劳分析,将存活率定为 97.5%。由于 FEMFAT 软件中,疲劳寿命的计算方式是应力循环次数与最大疲劳损伤值的比值,在弹性变形阶段,循坏次数与最大疲劳损伤值成正比,因此为了计算方便,本文将应力循环次数定为 1 次。分析结果表明,在应力循环一次的条件下,最大的疲劳损伤值为 0.000 392 6,则完整球壳的使用寿命为:
| $\frac{{{\text{应力循环次数}}}}{{{\text{最大疲劳损伤值}}}} = \frac{{\rm{1}}}{{{\rm{3}}{\rm{.926}} \times \mathop {{\rm{10}}}\nolimits^{{\rm{ - 4}}} }} = {\rm {2 \ 547} \text{次}}{\text{。}}$ |
结果显示球壳在下海来回 2 527 次后,会发生疲劳断裂,即发生疲劳失效。
对开孔球壳加强后进行疲劳分析的结果显示,同样在应力循环一次的条件下,最大的疲劳损伤值为 0.000 581,则开孔加强后的耐压球壳使用寿命为:
| $\frac{{{\text{应力循环次数}}}}{{{\text{最大疲劳损伤值}}}} = \frac{{\rm{1}}}{{{\rm{5}}{\rm{.810}} \times \mathop {{\rm{10}}}\nolimits^{{\rm{ - 4}}} }} = {\rm {1 \ 722} \text{次}}{\text{。}}$ |
将开孔前后疲劳分析结果进行对比可知,开孔加强后的耐压球壳寿命降低了 32.4%。
|
|
表 4 完整球形耐压壳与开孔加强球壳疲劳分析结果对比 Tab.4 The fatigue analysis and comparison of complete spherical shell and strengthened spherical shell with opening |
1)在 7 km 水深中,完整球形耐压壳的最大应力为 717.1 MPa,开孔加强后的球形耐压球壳的最大应力为 792 MPa。此结果说明开孔加强后的耐压球壳与完整球壳的强度相比仅下降了 9.4%,表明围壁加强的方式是有效的。
2)根据屈曲模态分析的结果,完整球形耐压壳的一阶屈曲模态值为 7.57,开孔加强后的球形耐压壳的一阶屈曲模态值为 6.12。即完整球形壳和开孔加强球壳都在近 600 MPa 载荷下,球壳才会出现失稳状态。上述表明在 7 km 水深中,材料强度是影响完整球形耐压壳与开孔加强后的耐压壳的寿命的主要因素,且开孔加强后的耐压球壳稳定性与完整球壳相比下降了 19%。
3)以强度为基准,分别对完整球形耐压壳和开孔加强后的球形耐压壳进行疲劳分析,得出使用寿命分别为 2 547 次和 1 722 次。说明对开孔的球形耐压壳进行围壁加强后,使用寿命与完整球形耐压壳相比下降了 32.4%。表明开孔加强设计对球形耐压壳的疲劳寿命影响较大。研究成果可为深海球形耐压壳开孔开窗设计提供参考。
| [1] |
张建, 高杰, 王纬波, 等. 深海球形耐压壳力学特性研究[J]. 中国造船, 2015(4): 129–140.
ZHANG Jian, GAO Jie, WANG Wei-bo, et al. Investigation on mechanical properties of deep sea sPherical pressure hull[J]. Shipbuilding of China, 2015(4): 129–140. |
| [2] | 中国船级社. 潜水系统和潜水器入级与建造规范[S]. 北京: 人民交通出版社, 1996. |
| [3] | 王自力, 王仁华, 俞铭华, 等. 初始缺陷对不同深度载人潜水器耐压球壳极限承载力的影响[J]. 中国造船, 2007(2): 45–50. |
| [4] | 俞铭华, 王仁华, 王自力, 等. 深海载人潜水器有开孔耐压球壳的极限强度[J]. 中国造船, 2005(4): 92–96. |
| [5] |
张建, 王明禄, 王纬波, 等. 蛋形耐压壳力学特性研究[J]. 船舶力学, 2016(Z1): 99–109.
ZHANG Jian, WANG Ming-lu, WANG Wei-bo, et al. Research on mechanical properties of the eggshell-shaped pressure hull[J]. Ship Mechanics, 2016(Z1): 99–109. |
| [6] | PAN B B, CUI W C. An overview of buckling and ultimate strength of spherical pressure hull under external pressure [J]. Marine Structures, 2010, 23(3): 227–240. |
| [7] | WANG C M, WANG C Y, REDDY J N. Exact solutions for buckling of structural members [M]. CRC Press, 2004. |
| [8] | TIMOSHENKO S P, GERE J M. Theory of elastic stability [M]. Dover Publications, 1961. |
| [9] | 王文涛, 上官文斌, 段小成, 等. 基于线性疲劳累计损伤橡胶悬置疲劳寿命预测研究[J]. 机械工程学报, 2012(10): 56–65. |
| [10] | 高云凯, 徐成民, 方剑光. 车身台架疲劳试验程序载荷谱研究[J]. 机械工程学报, 2014(4): 92–98. |
| [11] |
周海波, 彭云飞, 吴鸿敏, 等. 圆柱壳变形计算方法研究[J]. 舰船科学技术, 2016, 38(5): 1–4.
ZHOU Hai-bo, PENG Yun-fei, WU Hong-min, et al. Research on calculation methods of cylindrical shell Deformation[J]. Ship Science and Technology, 2016, 38(5): 1–4. |
 2017, Vol. 39
2017, Vol. 39
