2. 水下信息与控制重点实验室, 陕西 西安 710075
2. Science and Technology on Underwater Information and Control Laboratory, Xi'an 710075, China
潜艇目标强度(TS)是水中兵器探测和目标隐身技术中的一个基本指标,反映了目标对声波散射的总体情况[1]。由于潜艇目标的外形较复杂,在水中兵器跟踪并攻击潜艇过程中,受潜艇姿态变化等因素的影响,其散射特性呈现出随机不规律的起伏,计算目标强度很难用严格的和复杂的公式来确切表达[2]。通常的实验测量及理论计算,仅给出了目标强度的一个确定值,无法描述目标强度的随机性和起伏性。这样的模型在实际工程应用和实验数据分析过程中,不仅不能反映目标强度的实际随机情况,而且存在较大的误差。因此,研究目标强度的统计特性对潜艇目标强度的预报更具有实际意义。
近年来,上海交通大学范军教授团队针对目标强度测量结果是随方位角变化而快速起伏的随机变量,也就是目标强度对方位角非常敏感的情况,将雷达散射面积(RCS)的概念延伸到水声领域,提出了声呐散射面积(SCS)的概念,借鉴雷达散射截面统计模型建立面向任意目标的声呐散射截面起伏统计模型[3]。是国内首次在水声领域对目标强度统计模型开展的研究,弥补了以往目标强度预报模型是确定性模型的不足,预报结果在一定程度上反映了目标强度的随机性和起伏性,提高了模型在实际工程应用和实验数据分析中的准确性。
本文采用板块元法对潜艇目标强度进行快速预报,将潜艇目标强度等效成潜艇表面若干面元散射强度的叠加,进而获得各个采样角度下的潜艇目标强度,将得到的目标强度值作为统计建模的样本。针对直方图统计模型精度的受区间划分和样本数量影响较大的问题,本文采用 Parzen 窗估计法建立基于样本值的统计模型,获得了典型舷角下的目标强度分布估计曲线,并对潜艇目标强度的统计分布特性进行分析,仿真结果表明,采用 Parzen 窗估计法建立的潜艇目标强度统计模型比直方图模型更加准确和有效。
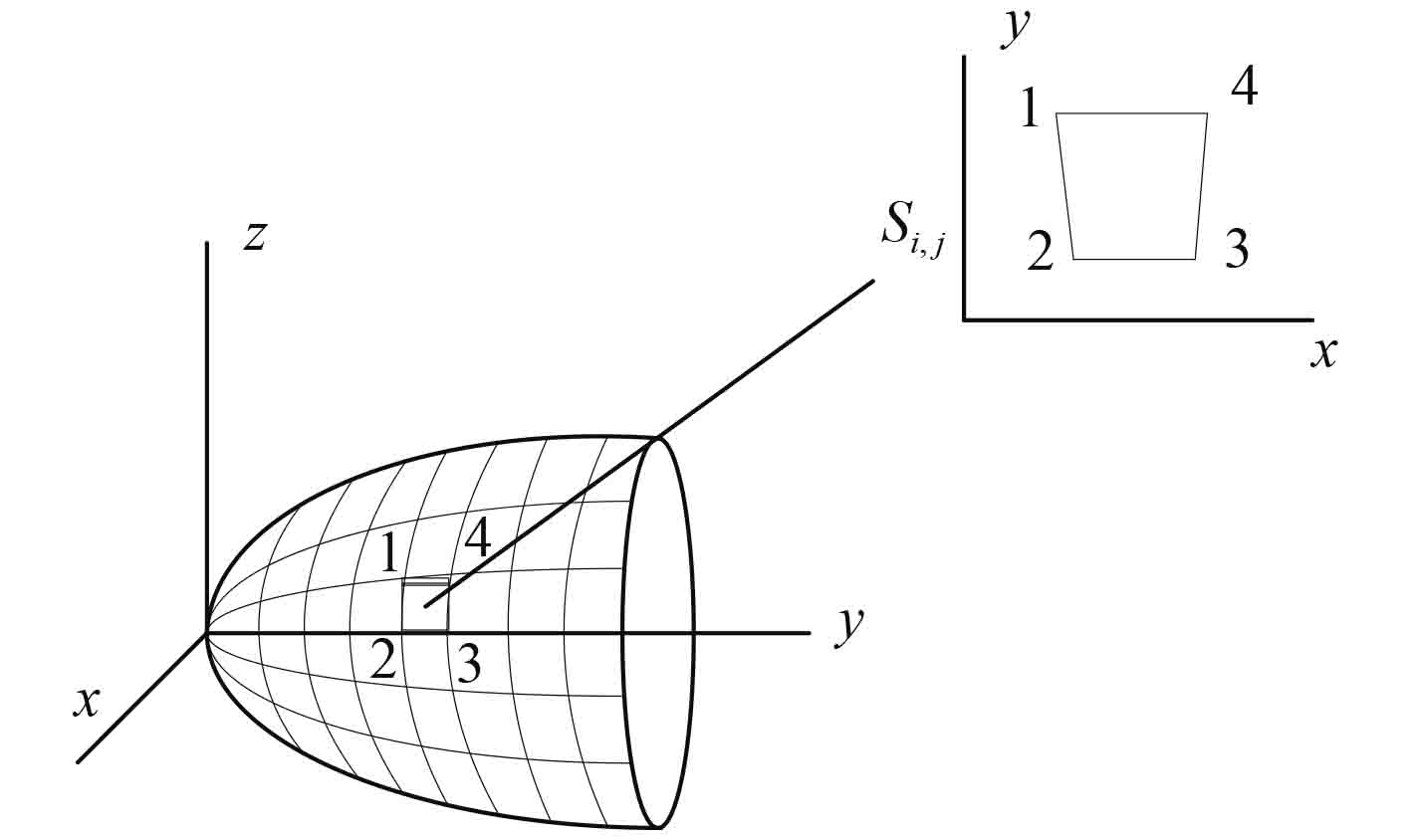
1 理论基础 1.1 目标强度板块元计算采用板块元法计算目标强度时,将目标表面划分为G ×H 个网格,得到一系列面元Si,j,其中i=1,2,…,G,j=1,2,…,H。将空间中的面元Si,j 转化到XOY 平面,则面元法线与Z 轴重合,面元Si,j 的目标强度面积为ISi,j。对所有面元的散射声场求和得到目标散射声场的近似值[4]。
|
图 1 网格划分及坐标转换 Fig. 1 Meshing and coordinates conversion |
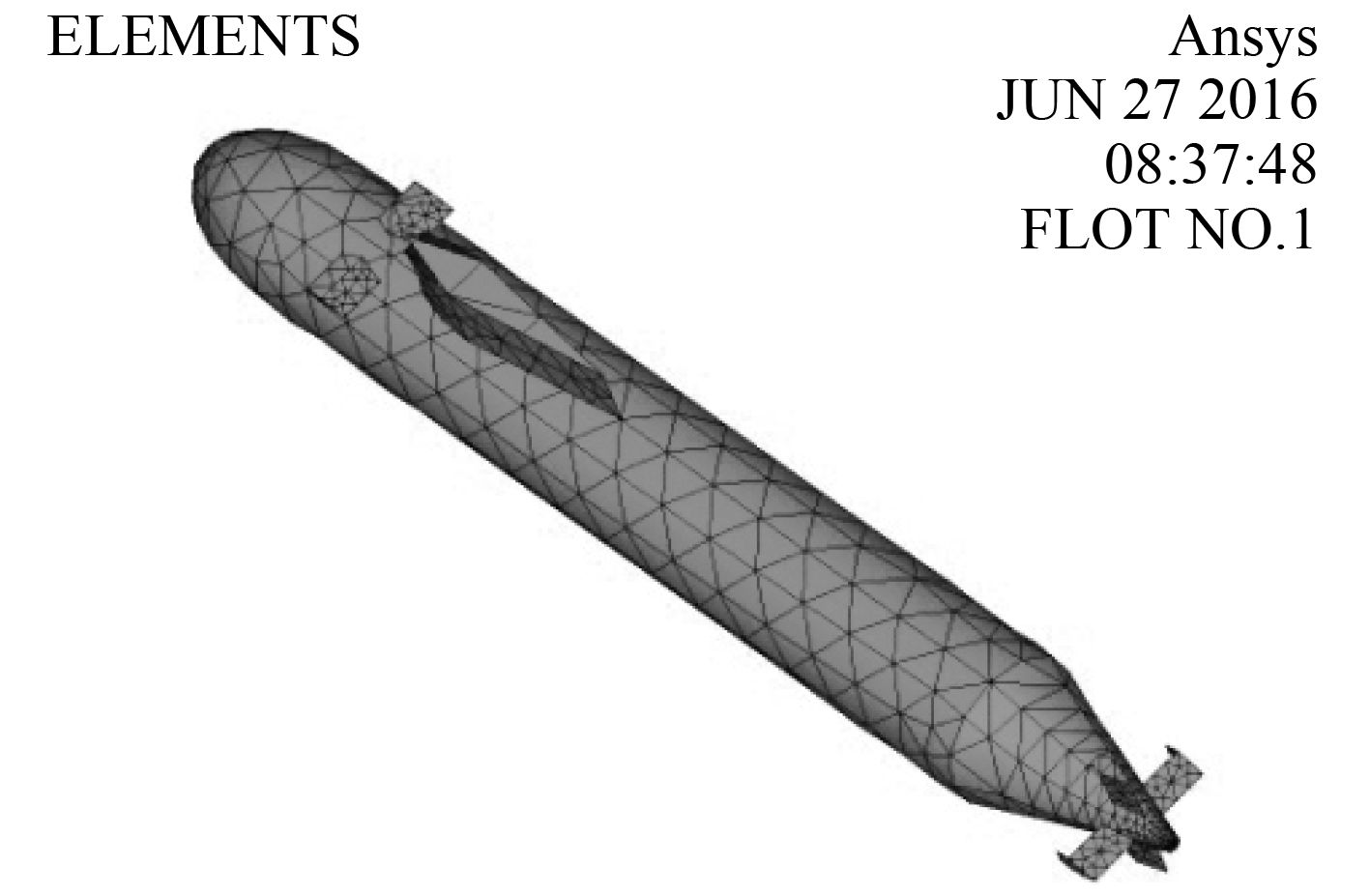
用 UG 对潜艇目标进行三维几何建模,利用有限元分析软件 Ansys 对潜艇表面进行网格划分。导出节点和网格信息后,可以采用板块元法对目标强度进行计算,相关计算结果可作为统计分析的样本值。
|
图 2 Ansys 潜艇模型网格划分 Fig. 2 Submarine model meshing in Ansys |
统计分布密度估计是根据观测数据而对其假定的概率函数进行估测。本文对目标强度采用直观简便的直方图法进行密度估计。
直方图是将整个数据空间划分为格网单元,认为数据均匀分布的假设在每个单元内成立[5]。首先定义以下信息:一个样本数据集D;数据集D 中所有数据项的数目N;数据覆盖范围C。
利用直方图法对样本数据进行统计分析时,通常步骤如下:
1) 将样本数据值覆盖的数据区间C 分成几个等子区间。
2) 对样本集D 内的N 个样本数据进行从小到大的排序,按照顺序依次判断样本数据值落到这个相应的子区间,这个子区间的高度就相应的加一个单位的高度。
3) 将各个子区间的高度进行归一化,建立直方图的概率统计模型。
采用以上方法,可以利用样本数据构造出基于直方图的概率密度函数。
1.3 Parzen 窗估计原理直方图估计的密度函数不平滑,且密度函数受子区间宽度影响很大。资料表明,核密度估计(Kernel density estimate)可有效解决该问题。核密度估计属于一种非参数的估计方式:对某一已知的密度函数,在观测点上平均化,以期得到一条光滑的估计曲线。
假设样本数据值在D 维空间服从一个未知的概率密度函数,则其在区域R 内的概率为:
| $ P=\int {p\left( x \right){\rm d}x} \text{,} $ | (1) |
假设N 个样本数据点有K 个落入了区域R,那么就应该服从二项分布:
| $ Bin\left( {K|N,P} \right)=\frac{{N!}}{{K{\rm{!}}\left( {N - K} \right)!}}{P^K}{\left( {1 - P} \right)^{1 - K}}\text{,} $ | (2) |
由概率知识可知,在样本数N 足够大时,K ≈N ×P。其中,若假设区域R 足够小时,P ≈p(x)×V,V 为区域R 的空间。将两式结合可得:
| $ {\mathop{\rm p}\nolimits} \left( x \right)=\frac{K}{{NV}}\text{。} $ | (3) |
根据该式来估算密度函数p(x)有以下 2 种方法:
1) K 不变,通过决定区域V 的大小来估算密度函数。
2) V 不变,通过决定K 的大小来估算密度函数。
本文假定区域R 不变,即V 不变,可得估计的密度函数为[6]:
| $ p\left( x \right)=\frac{1}{N}\sum\limits_{n=1}^N {\frac{1}{{{h^D}}}k\left( {\frac{{x - {x_n}}}{h}} \right)} \text{,} $ | (4) |
式中:V =hD ;D 为数据维数;h 为区域V 的超立方体的棱长,此处k 取最优窗函数,其宽度为样本数据范围的 100 等分。本文选取正态分布窗函数作为最优窗函数,考虑均值为 0,方差为 1 的一位正态分布,则该窗函数的表达式如下:
| $ k\left( u \right)=\frac{{\rm{1}}}{{\sqrt {2 } }}{\rm{exp[ - }}\frac{1}{2}{{\mathop{u}\nolimits} ^2}] \text{。}$ | (5) |
该密度函数估计方法称为 Parzen 窗估计法,该方法的实质是用正态分布窗函数代替样本值来估计整体的概率密度分布,其原理如图 3 所示。

|
图 3 Parzen 窗估计法原理图 Fig. 3 Schematic diagram of Parzen window estimation method |
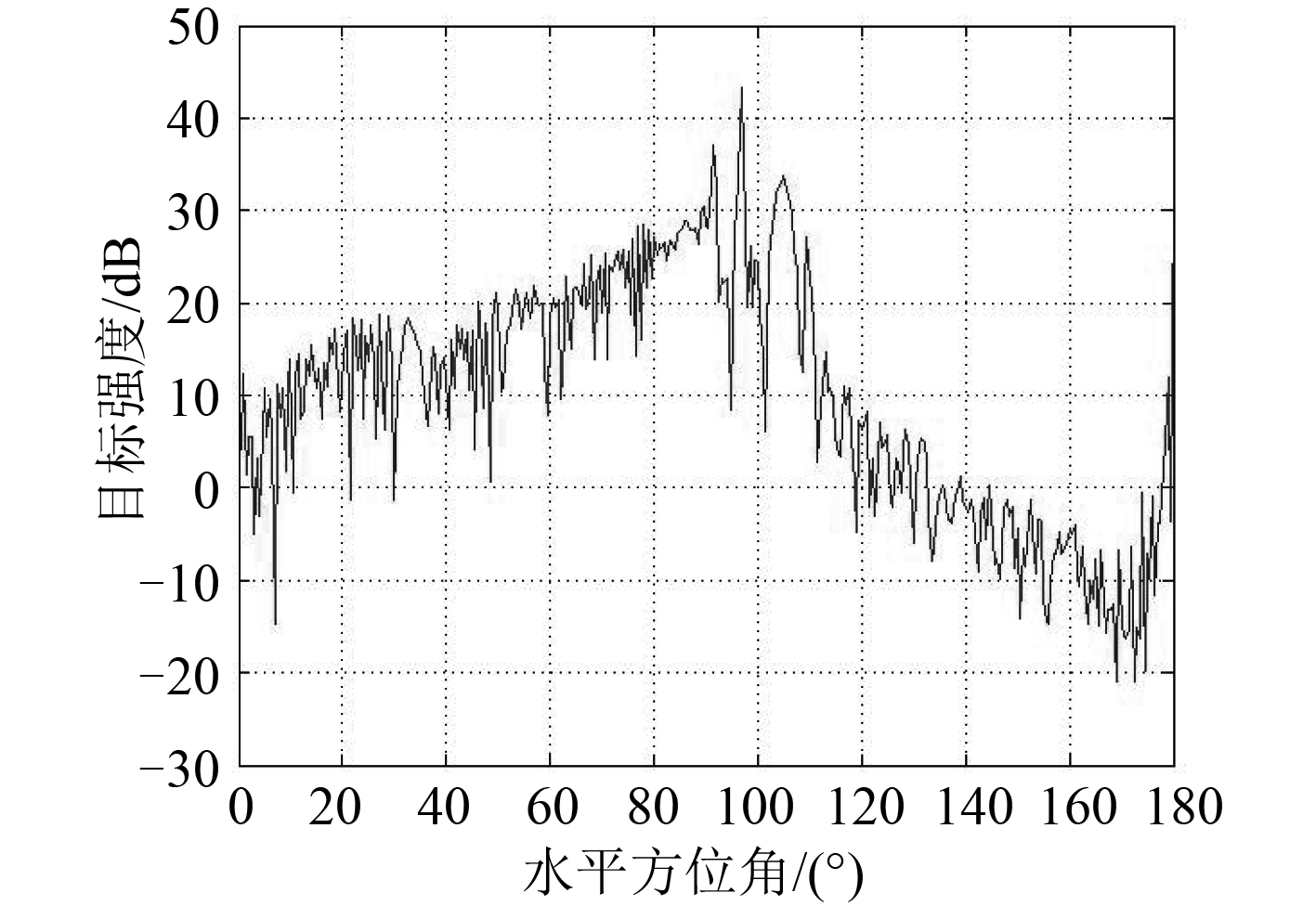
建立国际通用标准的 Benchmark 潜艇(以下简称潜艇)三维模型,艇长 62 m,艇身围壳直径 7.5 m。将潜艇表面划三角形面元,面元尺寸为 ∆,设置仿真条件满足 ∆/λ ≤ 0.533,其中λ 为入射波波长,以控制计算结果在一定误差范围[7]。用板块元法对 benchmark 潜艇 0°~180° 范围内每隔 0.5° 的目标强度进行计算。图 4 为潜艇的水平方位目标强度曲线。
|
图 4 潜艇目标强度曲线 Fig. 4 Submarine target strength graph |
由图 4 可知,潜艇目标强度对水平方位角敏感,具有明显的离散性且起伏剧烈;潜艇中部的平均目标强度值最大,在首部和尾部附近的平均目标强度较小,符合潜艇目标强度经典蝶形图分布特征。针对各个舷角目标强度的起伏特性,下面首先采用直方图法建立典型舷角下的目标强度分布模型。
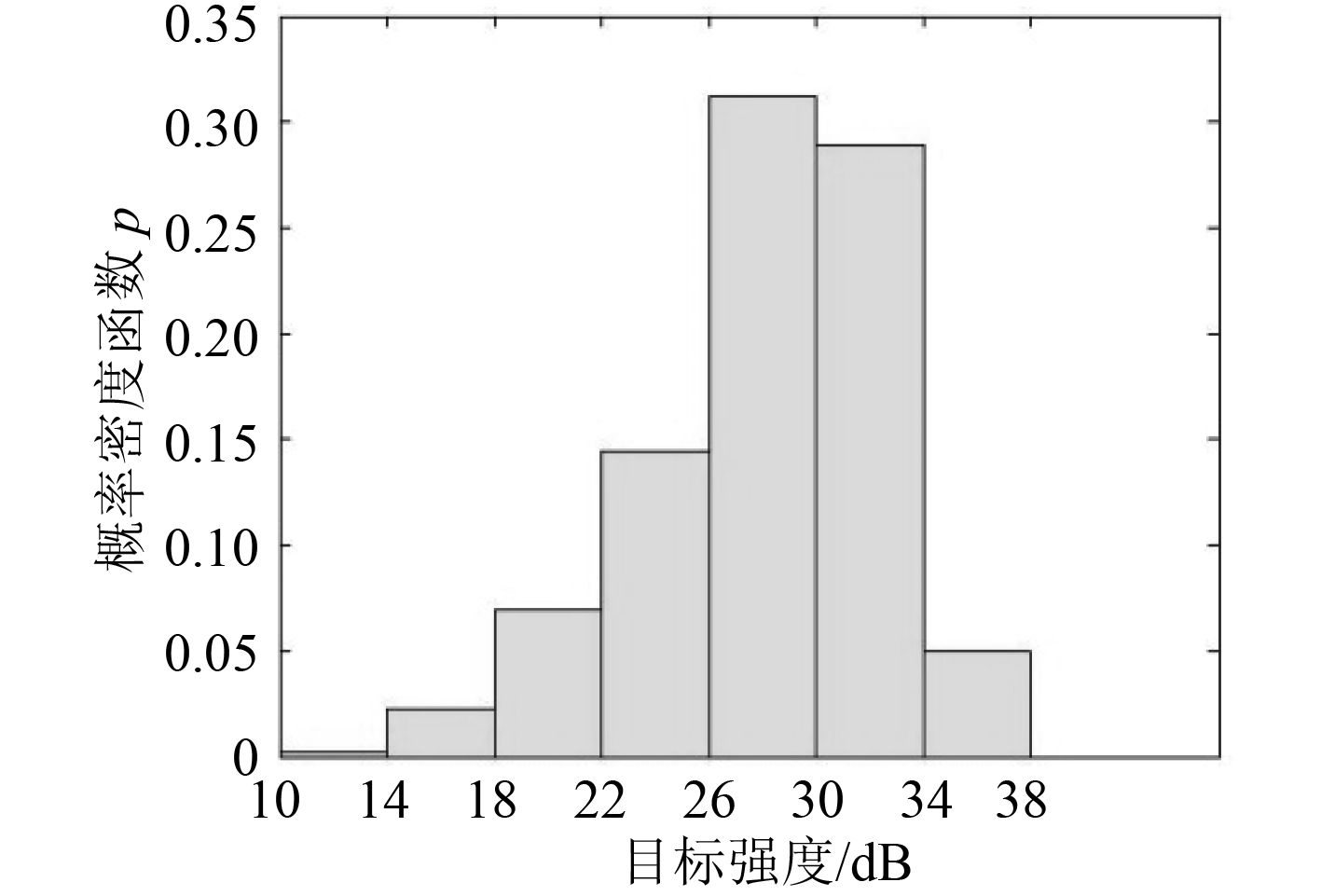
2.1 典型舷角下的直方图统计建模考虑鱼雷攻击潜艇时主动声呐的实际工作频带,以某频率下 88°~92° 范围的目标强度计算结果作为艇中部目标强度值,以 0.01° 间隔采样计算,得到 401 组数据,在此基础上建立概率密度直方图的统计模型,其中d(单位 dB)为直方图区间划分宽度,仿真结果如图 5~图 7所示。
|
图 5 d=4 时中部目标强度分布 Fig. 5 TS distribution in midship whend=4 |
|
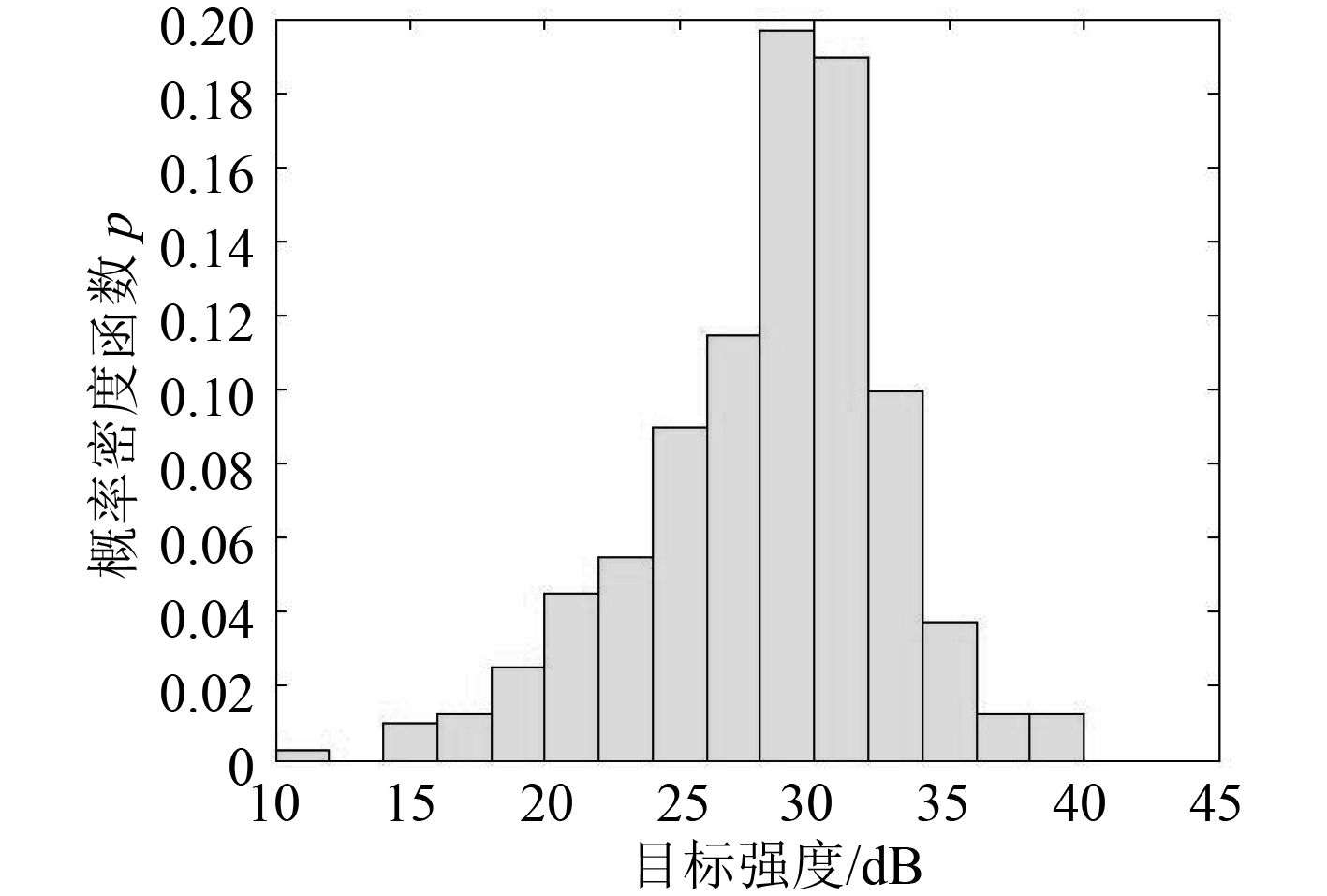
图 6 d=2 时中部目标强度分布 Fig. 6 TS distribution in midship whend=2 |
|
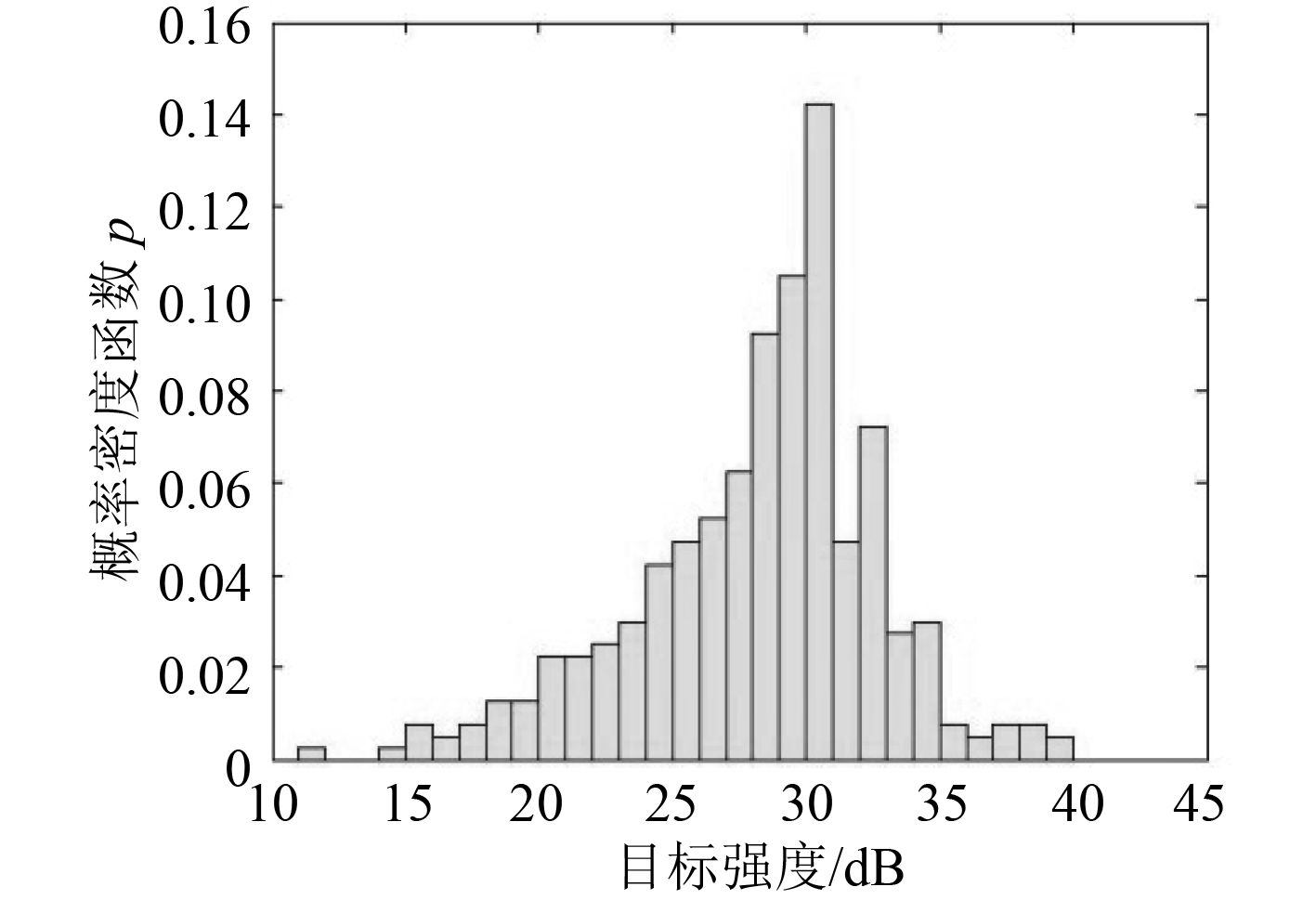
图 7 d=1 时中部目标强度分布 Fig. 7 TS distribution in midship whend=1 |
由图可知,直方图区间宽度的大小影响密度函数估计的性能。区间宽度为 4 时,得到的目标强度的密度函数估计不够精确,区间宽度为 1 时,直方图法得到的密度函数相对精确,也比较平滑。随着区间宽度的减小,直方图表示的模型会更加精确,但直方图在某些地方可能会出现幅值变化不连续甚至概率密度函数为 0 的情况,不符合潜艇目标强度概率连续变化的分布特性。为此,下文采用 Parzen 窗估计法对潜艇目标强度进行建模研究,首先对 Parzen 窗估计法的有效性进行验证。
2.2 Parzen窗估计法有效性验证下面对 Parzen 窗估计方法的有效性进行验证。以正态分布为例,进行仿真,说明该方法的有效性。仿真条件设置如下,生成 1 000 个服从正态分布的随机数,从中分别随机抽取个数为N=20,100,500 的数作为样本。分别采用频率直方图和 Paezrn 窗估计法对 3 个不同样本数的样本建立概率密度分布模型,并与正态分布密度函数进行对比,仿真结果如图 8~图 10 所示。
|
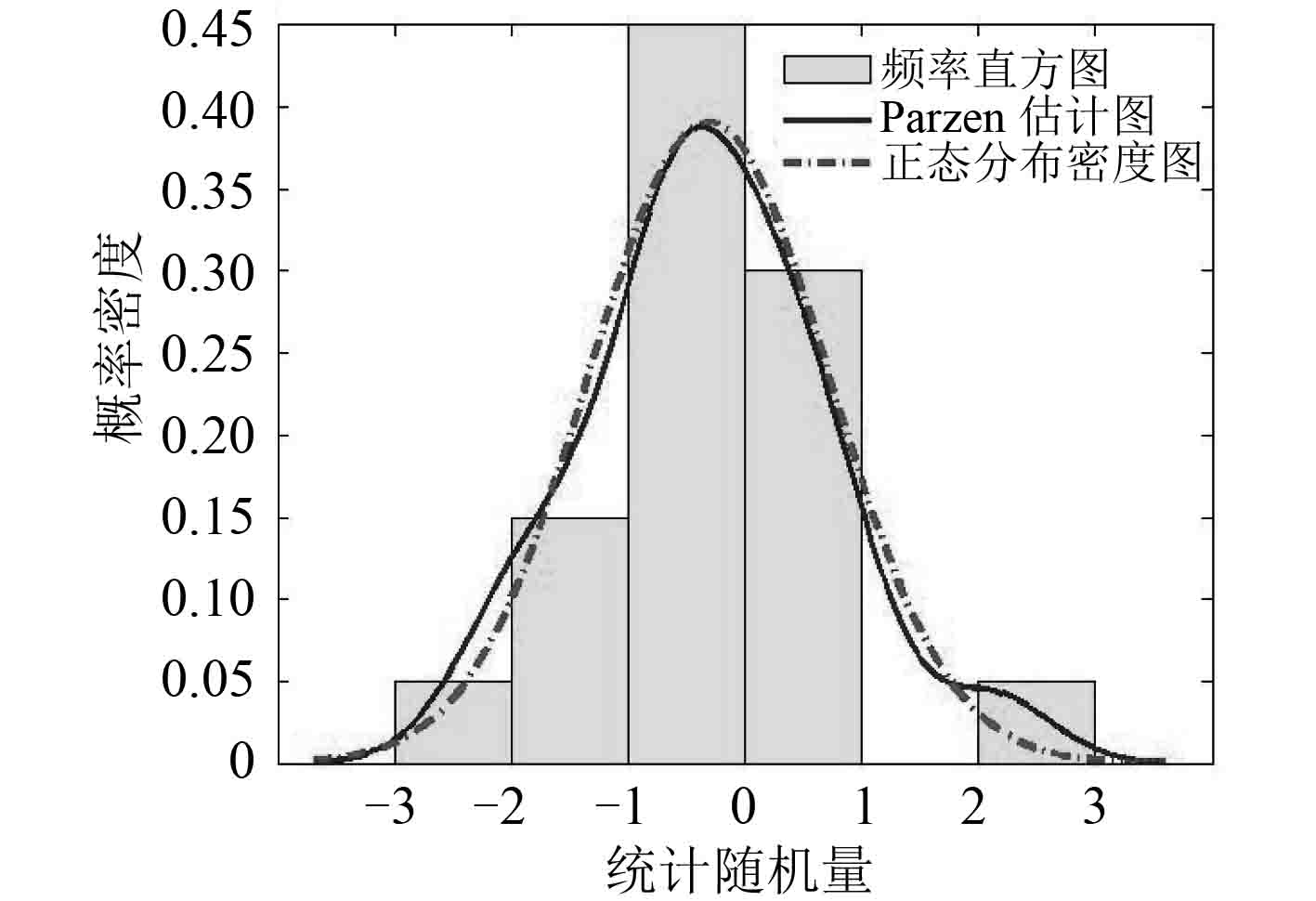
图 8 样本数N=20 Fig. 8 Sample numberN=20 |
|
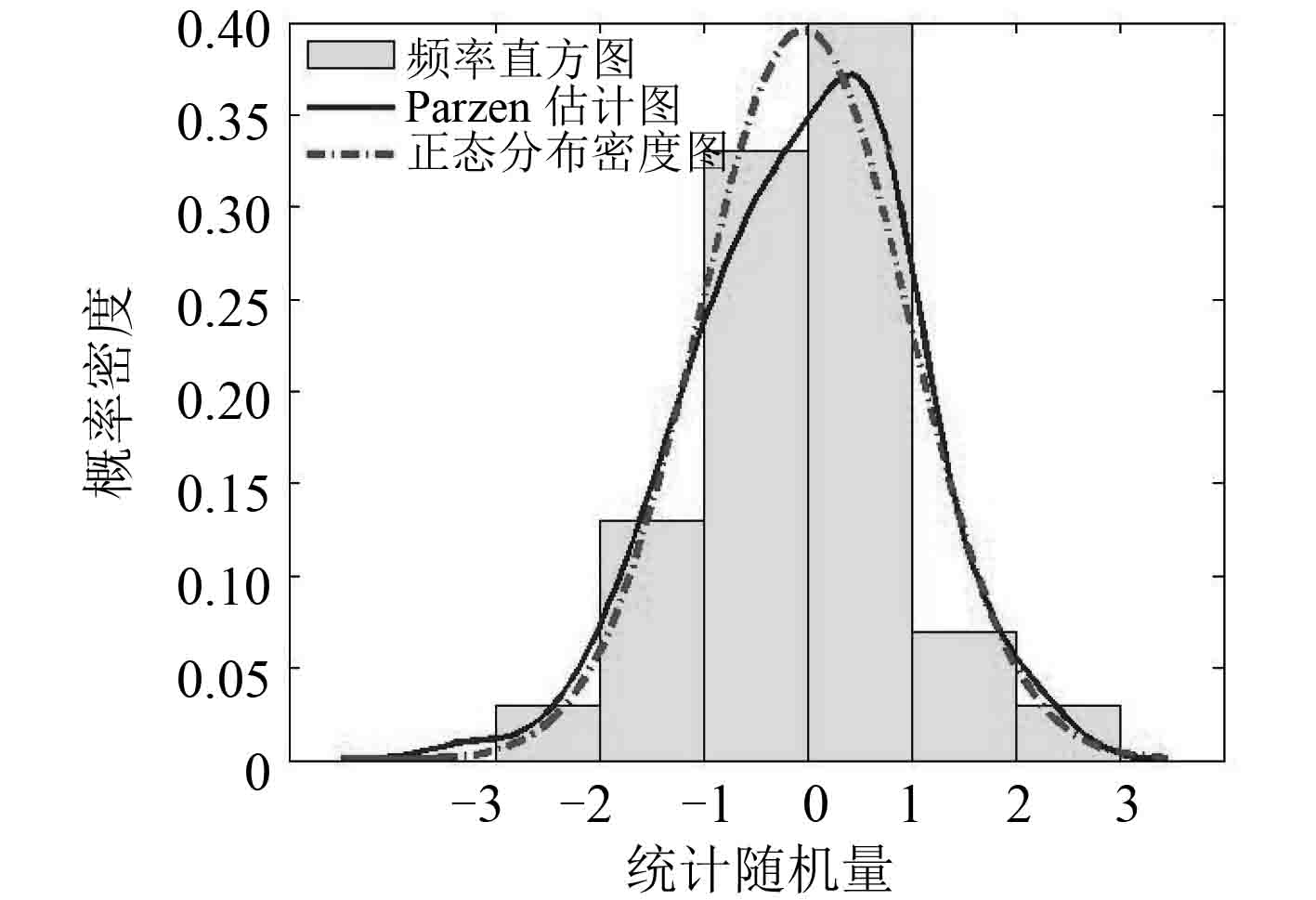
图 9 样本数N=100 Fig. 9 Sample numberN=100 |
|
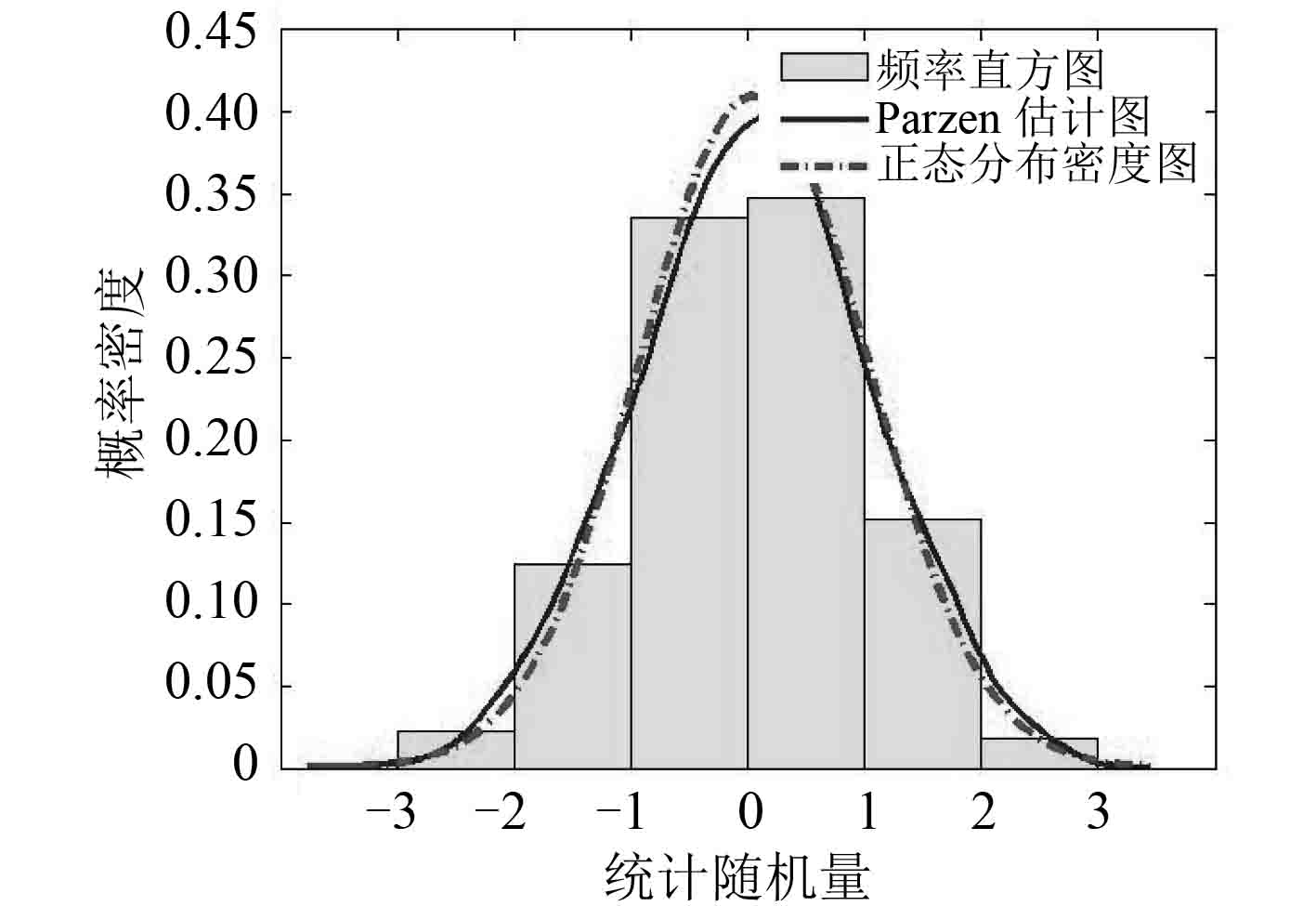
图 10 样本数N=500 Fig. 10 Sample numberN=500 |
通过以上示例的仿真结果可知,当样本数较小时,直方图不能反映真实的密度分布特征,随着样本数的增加,频率直方图逐渐接近标准正态分布。但 Parzen 窗估计法可在样本数较小的时候较好地反映随机抽取的样本数据分布特征以及真实概率密度分布特征,并不受区间长度的影响。当样本数趋于无穷大时,频率直方图法与 Parzen 窗估计法的结果与实际密度分布函数趋于一致[8]。
2.3 Parzen 窗估计法建模与计算下面采用核密度估计方法,对样本数据进行估计,在此基础上对估计密度函数的统计规律和参数进行研究,给出其概率密度分布(PDF)和累积概率分布(CDF)。
分别建立区间宽度为 2 的直方图分布模型和窗函数估计模型,如图 11~图 14所示。
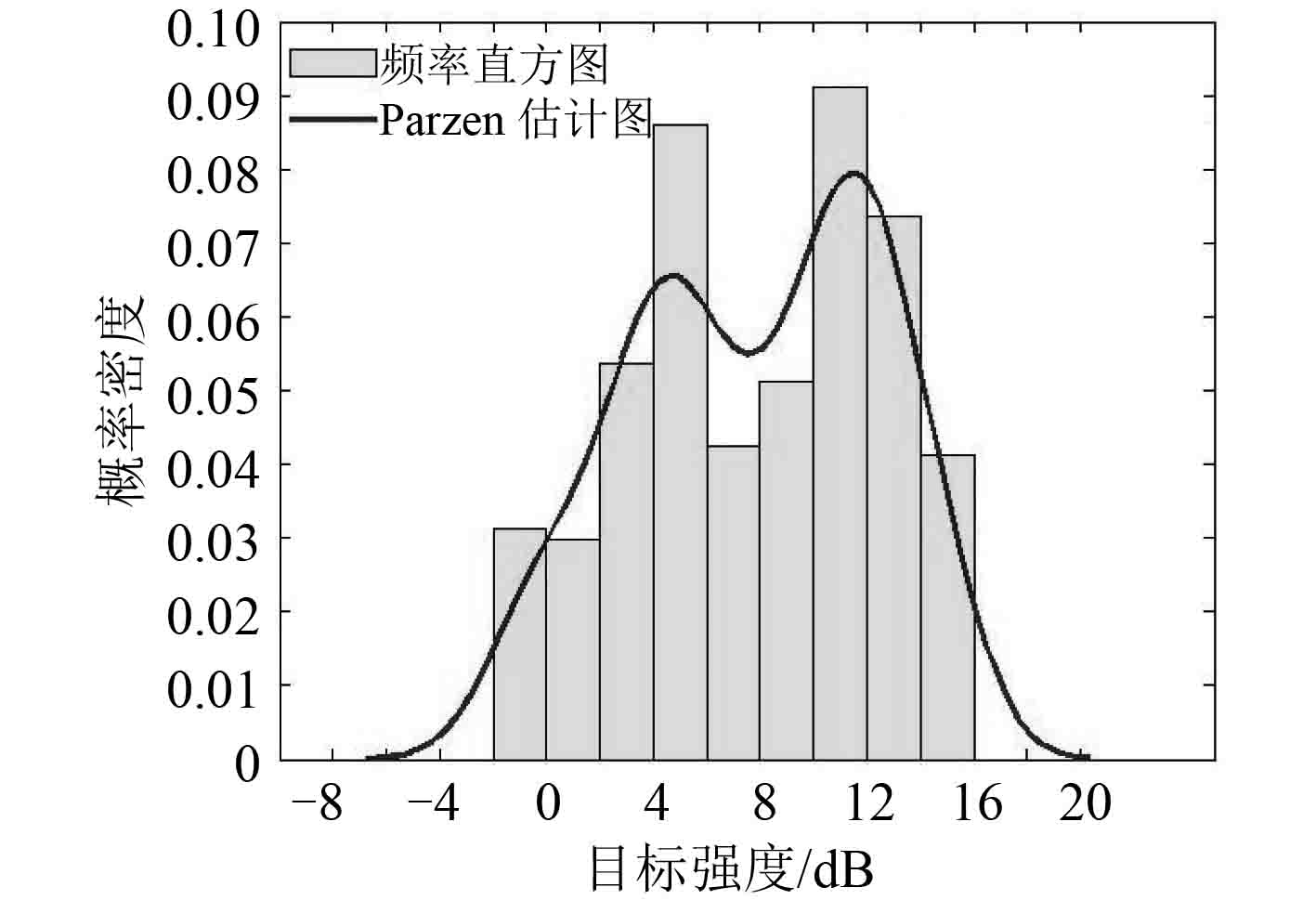
|
图 11 首部目标强度分布 Fig. 11 TS distribution in bow |
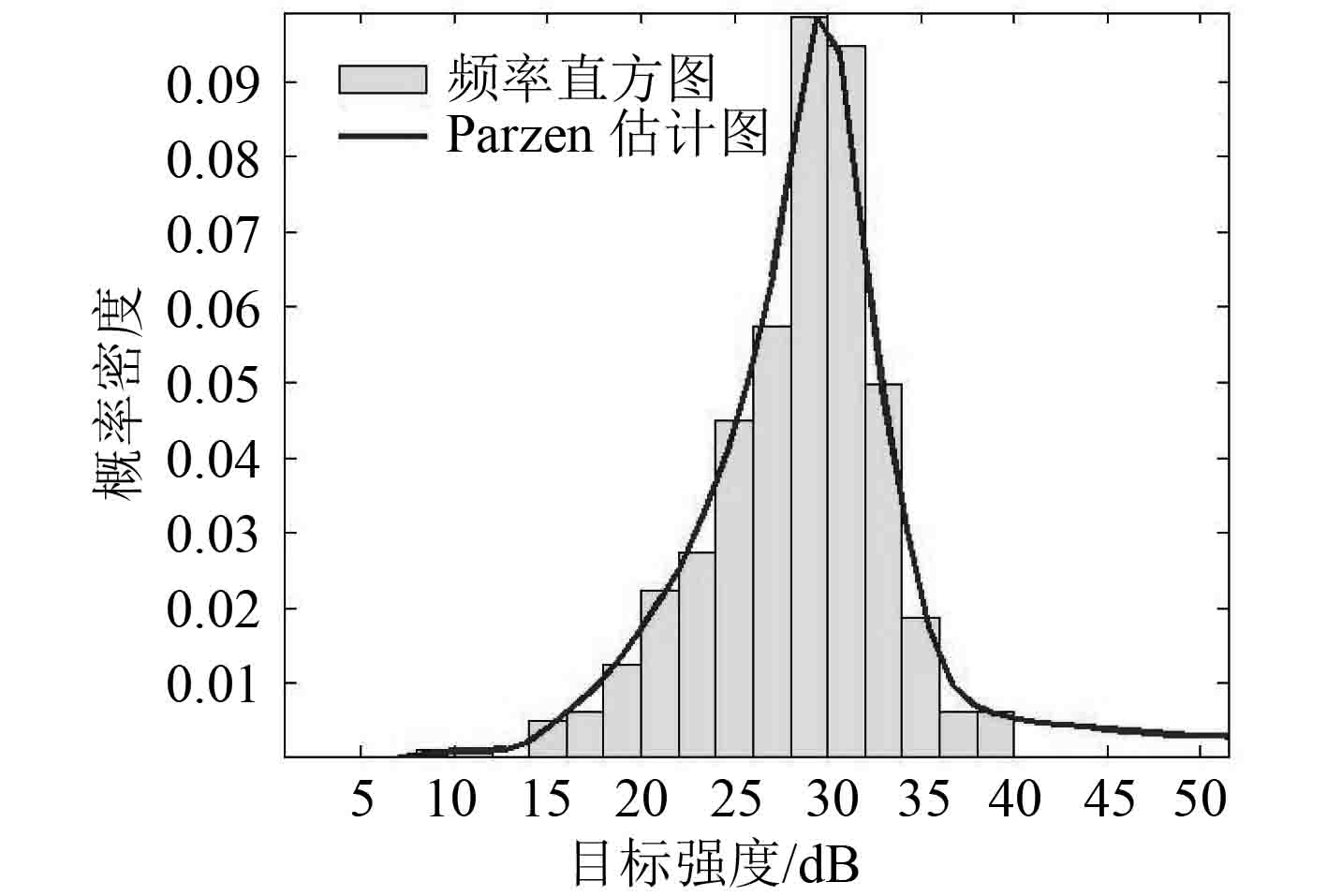
|
图 12 中部目标强度分布 Fig. 12 TS distribution in midship |
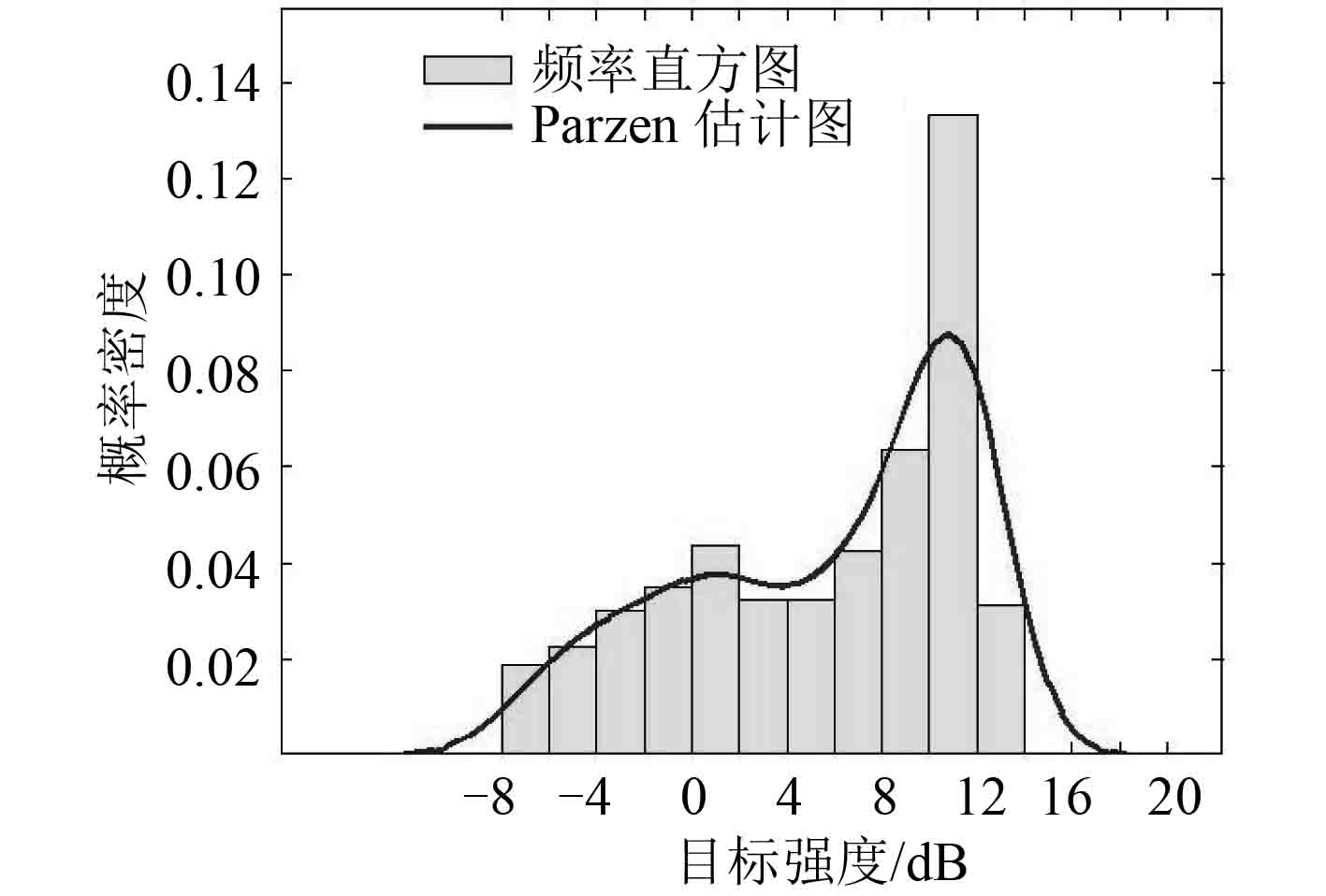
|
图 13 尾部目标强度分布 Fig. 13 TS distribution in stern |
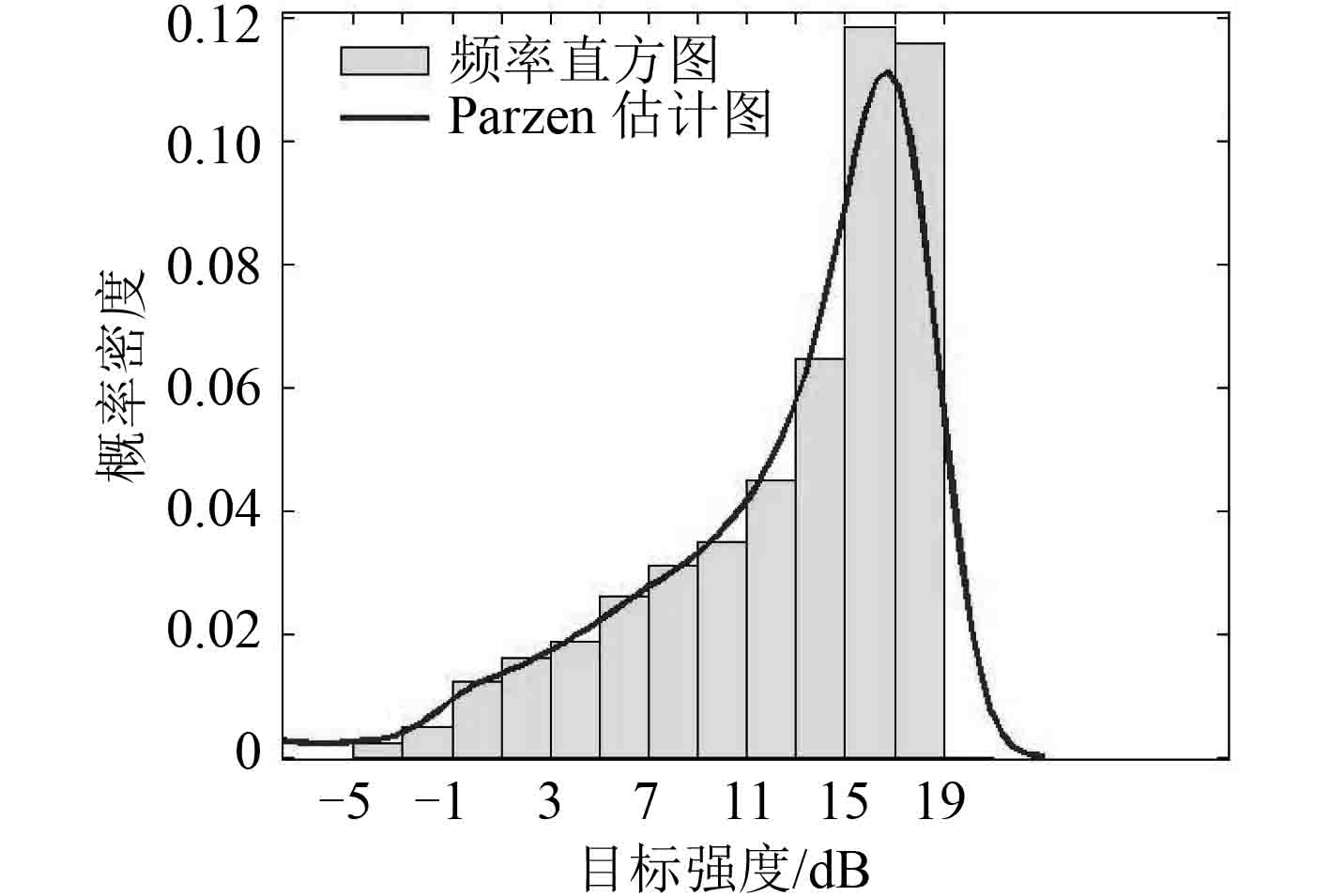
|
图 14 30° 舷角目标强度分布 Fig. 14 TS distribution in bow bearing of 30° |
1) 潜艇中部的平均目标强度最大,其次是 30° 舷角处的平均目标强度,均高于艇首和艇尾的平均目标强度,各个典型舷角下的目标强度分布具有连续性,仿真结果符合潜艇目标强度经典的蝶形图分布规律。
2) 潜艇在各个舷角的目标强度值均具有明显的起伏且在不同入射角度下的目标强度的密度分布特征各不一样,其中潜艇中部的目标强度分布较集中,首部和尾部目标强度分布范围较分散,符合目标曲率半径大小对目标强度变化的影响规律。
3) 采用 Parzen 窗估计法建立的潜艇目标强度分布模型较平滑和连续,便于提取统计参数,可直观有效地用于潜艇目标强度的统计分析。
3 结 语本文应用板块元法,通过合理的网格划分计算得到各个典型舷角下潜艇目标强度的样本值,采用 Parzen 窗估计法对目标强度密度函数进行估计,并对各典型舷角下的潜艇目标强度的统计分布特性进行分析。板块元计算结果符合潜艇目标强度经典蝶形图分布特征。仿真结果表明,对目标强度样本值采用 Parzen 窗估计法建立的分布模型比直方图法更加准确有效,可以更好地反映潜艇目标强度的统计分布特征。
| [1] |
何心怡, 张鹏, 王光宇, 等. 大俯仰角时的潜艇目标强度研究[J]. 舰船科学技术, 2007, 29 (3): 37–39.
HE Xin-yi, ZHANG Peng, WANG Guang-yu, et al. Target strength research of submarine under large pitching angle[J]. Ship Science and Technology, 2007, 29 (3): 37–39. |
| [2] |
张杨梅, 冯西安. 气泡群目标强度的起伏统计模型[J]. 计算机仿真, 2005, 32 (9): 14–18.
ZHANG Yang-mei, FENG Xi'an. Statistical model of target strength model of bubble cloud[J]. Computer Simulation, 2005, 32 (9): 14–18. |
| [3] |
李建龙. 水下目标的目标强度统计模型研究[D]. 上海:上海交通大学, 2013.
LI Jian-long. Research on the statistical model of target strength fluctuation of target strength fluctuation of underwater targets[D]. Shanghai:Shanghai Jiaotong University, 2013. |
| [4] |
王汝夯, 李冰, 魏强. 基于板块元的水面舰船远场声目标强度预报方法[J]. 声学技术, 2015, 34 (1): 6–10.
WANG Ru-hang, LI Bing, WEI Qiang. A method for predicting far-field target strength of surface ship based on planar elements theory[J]. Technical Acoustics, 2015, 34 (1): 6–10. |
| [5] |
赵瑶, 常发亮. 直方图统计方法的对比研究[J]. 计算机技术与自动化, 2007, 26 (4): 71–74.
ZHAO Yao, CHANG Fa-liang. The comparative study on histogram computation methods[J]. Computing Technology and Automation, 2007, 26 (4): 71–74. |
| [6] |
陈银超, 杨伟. 基于Parz窗估计的电液伺服作动器故障检测与健康评估[J]. 计算机测量与控制, 2012, 20 (8): 2083–2088.
CHEN Yin-chao, YANG Wei. Electric hydraulic servo actuator fault detection and health assessment based on parzen window estimation[J]. Computer Measurement & Control, 2012, 20 (8): 2083–2088. |
| [7] |
张文成, 周穗华, 陈聪聪, 等. 板块元法求目标散射特性中面元划分方法研究[J]. 武汉理工大学学报(交通科学与工程版), 2014, 38 (4): 878–882.
ZHANG Wen-cheng, ZHOU Hui-hua, CHEN Cong-cong, et al. Research on element partition of planar element method in target scattering characteristic calculation[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2014, 38 (4): 878–882. |
| [8] |
汤阿妮. 基于核密度估计算法的飞机载荷谱统计技术[J]. 北京航空航天大学学报, 2011, 37 (6): 654–657.
TANG A-ni. Technique of aircraft loads spectrum statistics based on kernel density estimation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37 (6): 654–657. |
 2017, Vol. 39
2017, Vol. 39
