无人水面艇(Unmanned surface vehicle,USVs)作为一种自主式小型船舶广泛应用于资源勘测、科学实验、探险、军事活动等领域[1-2]。通常,在无人水面艇自主运动中,航向控制是最基本的操纵运动。对无人水面艇的航向控制是基于岸基或者基于母船的控制中心来实现的。通过无人艇上的采样器采集首向角,首摇角速度、横摇角和舵角等状态信息并通过无线网络传输到控制中心,控制中心对采样器发来的航向信息进行构造并通过无线网络传输到舵机执行器,由舵机来执行操舵命令,完成航向的控制[3]。使用无线通信网络控制结构具有布线简单、结构灵活、成本低、便于维护和安装,相比传统控制系统中的点对点控制结构具有明显优势。因此,网络化控制系统在各个领域得到了广泛的应用[4-5]。然而,将网络引入无人水面艇的控制系统中不可避免地会产生网络诱导时延、数据包丢失[3]。这些现象可能对无人艇的航向控制系统性能(如稳定性、响应时间)产生负面影响。因此有必要研究网络诱导时延、数据包丢失等对无人水面艇的航向控制的影响。
对于无人艇在海上的航向问题,风、浪、流的干扰及网络特性(如网络诱导时延、丢包等)的影响会使无人艇产生航向的偏离,降低航向控制系统性能,甚至使系统不稳定,设计具有能使无人艇按照设定航向快速、稳定航行的控制器极其重要。目前针对无人艇的航向控制问题已取得一些成果。文献[6]采用非线性采样控制理论,设计了首摇和纵荡状态反馈控制律,使无人艇按照设定的航向航行。文献[7]针对喷水推进型无人艇的航向控制问题,在模型摄动和环境干扰下设计了具有鲁棒性的无人艇航向控制器。文献[8]应用自抗扰算法设计了无人水面艇的航向自动舵。文献[9]提出了一种反步自适应滑模控制方法,设计了单泵喷水推进型无人滑行艇的航向跟踪控制器。文献[10]将支持向量回归机(Support Vector Regression,SVR)引入无人艇的航向控制,提出自适应 SVR 逆控制方法,对无人艇航向进行有效控制。然而,这些文献研究的无人艇航向控制都是只考虑外部环境干扰并未考虑无人艇与岸基控制中心之间传输信息的无线通信网络因素,如网络诱导时延、数据丢包对航向控制的影响。
本文首次把网络因素引入航向控制领域,建立基于网络的无人艇航向控制系统模型。考虑无人水面艇自主运动中受到外部环境干扰及控制中心-执行器网络通道中存在的网络诱导特性(如时延、丢包等)影响,会降低无人艇航向控制系统性能,提出一种基于网络的无人艇航向控制策略,使无人艇能按照设定航向快速、稳定地航行。定义合适的 Lyapunov 泛函并利用凸分析方法,导出新的航向控制器设计准则。数值仿真验证了本文设计的航向控制器能使无人水面艇较快地跟踪设定的航向,并具有较强的抗干扰性和鲁棒性,较高的控制精度。
1 网络环境下无人水面艇航向控制模型建立 1.1 基于网络的无人水面艇航向控制系统原理对于网络环境下的无人水面艇航向控制系统,无人艇是由岸基的控制中心控制。如图 1 所示,采样器采集无人艇的航向角ψ(t)、首摇角速度r(t)等的状态信息,通过采样器-控制中心网络通道传输到控制中心,控制中心比较当前无人艇的航向和期望的航向并根据二者之差生成控制舵角信号,经控制中心-执行器网络通道,传输到执行器,操纵无人艇改变航向,直到当前航向与期望的航向相同。由于控制中心-执行器网络通道中存在网络诱导时延和丢包,会降低系统性能,影响航向控制系统的稳定性,给控制器的设计增加困难。故本文在建立基于网络的无人艇航向控制模型的基础上,设计无人艇航向控制器,提高航向控制系统性能。
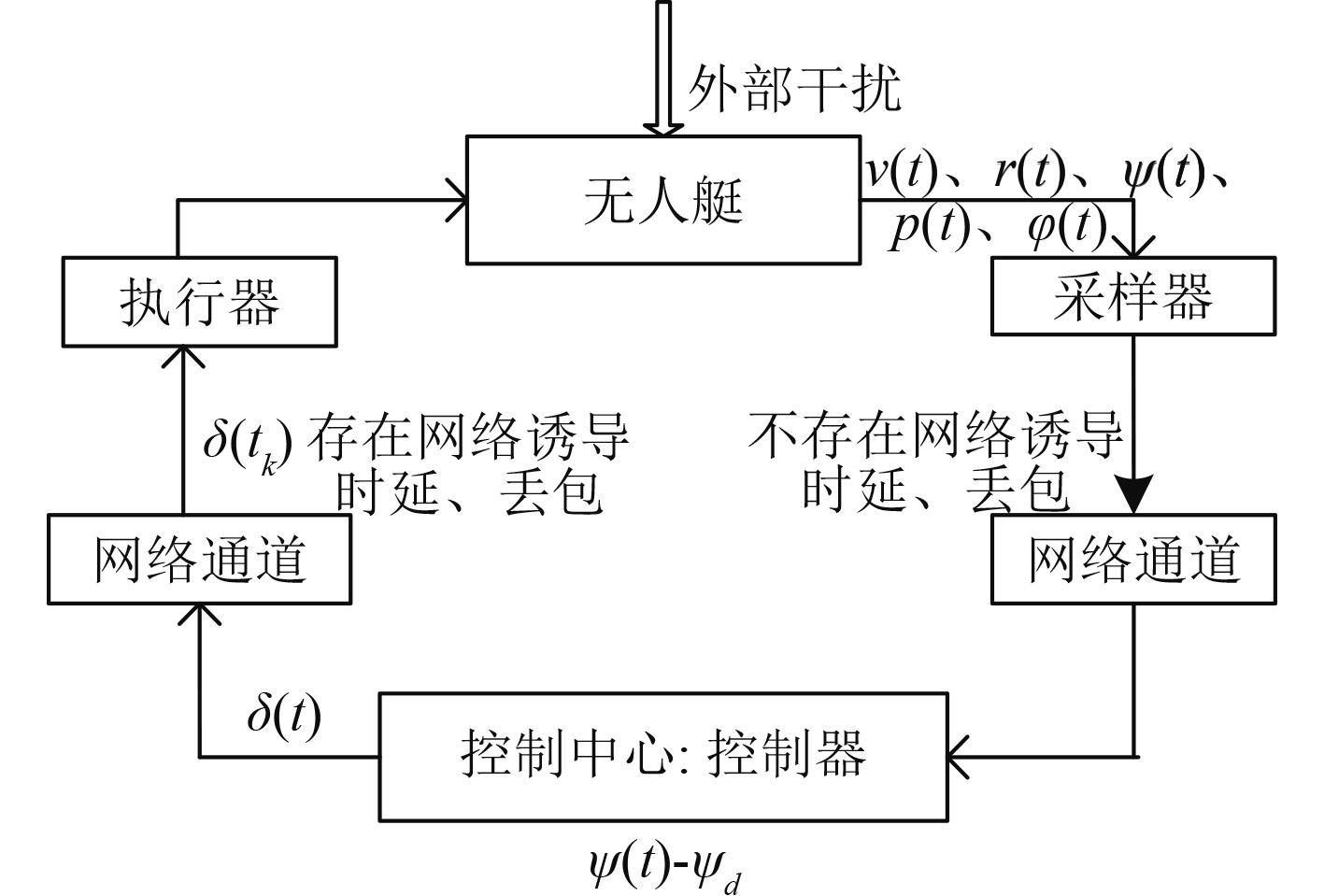
|
图 1 无人水面艇的航向控制系统框图 Fig. 1 The diagram of USV heading control system |
首先,建立外部环境干扰下无人水面艇的航向控制模型;其次,将网络因素引入航向控制模型,建立基于网络的无人艇航向控制模型。由于无人艇航向控制系统中引入网络,对它进行建模会比一般的船舶航向控制系统建模复杂。
海浪干扰下的船舶运动数学模型为[11]:
| $ \left\{ \begin{array}{l} v{\rm{(}}s) = \frac{{{K_{dv}}}}{{1+{T_v}s}}\delta {\rm{(}}s)\text{,}\\[5pt] \varphi {\rm{(}}s) = \frac{{\omega _n^2}}{{{s^2}+2\zeta {\omega _n}+\omega _n^2}}{\rm{[}}{K_{dp}}\delta {\rm{(}}s){\rm{+}}{K_{vp}}v{\rm{(}}s)+{\omega _\varphi }{\rm{(}}s)]\text{,}\\[5pt] \psi {\rm{(}}s){\rm{ = }}\frac{1}{{{\rm{(1+}}{T_r}s{\rm{)}}s}}{\rm{[}}{K_{dr}}\delta {\rm{(}}s){\rm{+}}{K_{vr}}v{\rm{(}}s)+{\omega _\psi }{\rm{(}}s)]\text{。} \end{array} \right. $ | (1) |
式中:v(s),ψ(s),φ(s),δ(s)分别为v(t),ψ(t),φ(t),δ(t)的拉普拉斯函数;v(t),ψ(t),φ(t),δ(t)分别为由舵单独引起的速度、航向角、横摇角与舵角;ωφ 和ωψ 分别为海浪对横摇和首摇的扰动;Tv 和Tr 为时间的传递函数;Kvp,Kvr,Kdr,Kdp 和Kdv 为增益;ζ 和ωn 分别为阻尼系数和自然频率。
将式(1)的传递函数转化为状态方程:
| $ \left\{ \begin{array}{l} \dot x(t){\rm{ = }}Ax(t){\rm{+}}B\delta (t){\rm{+}}E\omega (t){\text{,}}\\[5pt] x{\rm{(}}{t_{\rm{0}}}{\rm{) = }}{x_0}{\text{。}} \end{array} \right. $ | (2) |
式中:
| $\begin{array}{l} {{A}} = \left[ {\begin{array}{*{20}{c}} { - \frac{1}{{{T_v}}}} & 0 & 0 & 0 & 0\\[5pt] {\frac{{{K_{vr}}}}{{{T_r}}}} & { - \frac{1}{{{T_r}}}} & 0 & 0 & 0\\[5pt] 0 & 1 & 0 & 0 & 0\\[5pt] {\omega _n^2{K_{vp}}} & 0 & 0 & { - 2\zeta {\omega _n}} & { - \omega _n^2}\\[5pt] 0 & 0 & 0 & 1 & 0 \end{array}} \right],\;\\[5pt] {{B}} = {\left[ {\begin{array}{*{20}{c}} {{K_{dv}}/{T_{\rm{v}}}} & {{K_{dr}}/{T_r}} & 0 & {\omega _n^2{K_{dp}}} & 0 \end{array}} \right]^{\text{T}}},\;\\[5pt] {{E}} = {\left[ {\begin{array}{*{20}{c}} 0 & 0 & 0 & {\omega _n^2} & 0\\ 0 & {1/{T_r}} & 0 & 0 & 0 \end{array}} \right]^{\text{T}}}{\text{。}}\end{array} $ | (3) |
上面各个参数的物理意义同前文提到的一致。
对于无人水面艇的航向控制,控制输入为舵角δ(t),输出为航向角ψ(t)。考虑在受外部环境干扰的无人艇运动模型下,设置期望航向角为ψd,将期望的航向角ψd 和实际航向角ψ 作差即:z(t)=ψ(t)-ψd,于是将式(2)的状态方程转化为:
| $ \left\{ \begin{array}{l} \dot \xi (t) = \tilde { A}\xi {\rm{(t)+}}\tilde { B}u(t)+\tilde { E}\omega {\rm{(}}t){\text{,}}\\[5pt] \xi {\rm{(}}{t_0}{\rm{) = }}\xi {\rm{(0)}}{\text{,}}\\[5pt] z(t){\rm{ = }}C\xi (t){\text{。}} \end{array} \right. $ | (4) |
其中:状态
与常规的船舶航向控制不同,网络环境下的无人水面艇控制器是由岸基的控制中心(由控制器构成)来实现的。控制中心与执行器之间,采样器与控制中心之间都是通过网络来传递信息,由于无人水面艇航向控制系统中引入了网络,不可避免地会产生网络诱导时延和数据丢包。为了便于说明网络对无人艇航向控制系统的影响,特对网络环节做出如下假设:传感器和控制中心是都是时间驱动,采样周期都为h 且具有相同的采样时刻;执行器是事件驱动;没有数据包乱序;传感器和控制中心的网络通道不存在网络时延和丢包。
考虑采样器-控制中心之间的网络通道不存在网络诱导时延和丢包,而控制中心-执行器间的网络通道存在网络诱导时延和丢包。令控制中心的采样时刻[18]:tk,tk +h,tk+2h,tk+…,tk+1,tk+1 +h,tk+1+2h,tk+1+…(k = 0,1,2,…),假设控制输入信号在tk,tk+1,…时刻生成并成功的传输到无人水面艇,而在tk 和tk+1(k = 0,1,2,…)之间生成的控制输入丢失,设σca 为数据传输过程中发生的连续丢包数的上限,则对于
| $ \delta (t){\rm{ = }}u({t_k}){\rm{ = }}K\xi ({t_k}){\text{。}} $ | (5) |
式中:K 为控制器增益;τk 为岸基控制中心-执行器网络通道中的网络诱导时延,
对于
| $ \dot \xi {\rm{(}}t) = \tilde { A}\xi {\rm{(}}t{\rm{)+}}\tilde { B}K{\rm{(}}{t_k})+\tilde { E}\omega {\rm{(}}t){\text{,}} $ | (6) |
根据式(3)和式(5),则有基于网络的无人水面艇航向控制模型为:
| $ \left\{ \begin{array}{l} \dot \xi {\rm{(}}t) = \tilde { A}\xi {\rm{(}}t{\rm{)+}}\tilde { B}K{\rm{(}}t - \tau {\rm{(}}t))+\tilde { E}\omega {\rm{(}}t){\text{,}}\\[5pt] \xi {\rm{(}}{t_0}{\rm{) = }}\xi {\rm{(0)}}{\text{,}}\\[5pt] z{\rm{(}}t{\rm{) = }}{ C}\xi {\rm{(}}t{\rm{)}{\text{。}}} \end{array} \right. $ | (7) |
其中:时变时延τ(t)=t-tk,τm ≤τk <τM,对于
基于网络的无人艇航向控制模型(6)是本文与其他研究无人艇航向控制的主要区别。其他文献只考虑外部环境干扰,本文在考虑外部环境干扰基础上,考虑了控制中心-执行器网络通道中的网络特性(包括网络诱导时延和丢包)对无人艇航向控制系统的影响。
2 稳定性分析本节将运用 Lyapunov 稳定性分析方法,对基于网络的无人艇航向系统模型(6)作稳定性分析,给出系统渐进稳定的充分条件。
定理1:对于给定的标量τm,σca,τM 及h,如果存在对称正定矩阵P1,P2,P3,Q1,Q2,Q3,R1,R2,以及矩阵X1,X2,S 使得式(7)、式(8)和式(9)成立,则称无人艇航向控制系统(6)渐进稳定,并具有H∞ 性能范数界γ。
| $ \left[ {\begin{array}{*{20}{c}} {{P_1}} & {{P_2}}\\ * & {{P_3}} \end{array}} \right] > 0{\text{,}} $ | (8) |
| $ \left[ {\begin{array}{*{20}{c}} {{R_2}} & S\\ * & {{R_2}} \end{array}} \right] > 0 $ | (9) |
| $ \left[ {\begin{array}{*{20}{c}} {{\Xi _{11}}} & {{\Xi _{12}}}\\ * & {{\rm{ - }}{\gamma ^2}I} \end{array}} \right] \leqslant 0 $ | (10) |
其中:
| $ \begin{split} \\[-12pt] & {\Xi _{11}}{\rm{ = }}\left[ \!\!\!\!\!\!{\begin{array}{*{20}{c}} {{\Pi _{11}}} & {{\Pi _{12}}} & {{\Pi _{13}}} & {X_1^TBK} & 0 & {{\Pi _{16}}}\\ * & {{\Pi _{22}}} & 0 & {X_2^{\rm{T}}BK} & 0 & {{\tau _m}{P_2}}\\ * & * & {{\Pi _{33}}} & {{R_{\rm{2}}}{\rm{ - }}S} & S & {6{R_1}{\rm{ - }}{\tau _m}{P_3}}\\ * & * & * & {{\Pi _{44}}} & {{R_2} - S} & 0\\ * & * & * & * & {{\Pi _{55}}} & 0\\ * & * & * & * & * & { - 12{R_1}}\!\!\!\!\! \end{array}} \right],\\[5pt] & {\Xi _{12}}{\rm{ = }}{\vartheta _1}E+{\vartheta _2}E,\;\\[5pt] & {\Pi _{11}}{\rm{ = }}{P_2}+P_2^{\text{T}}+{Q_1}+{Q_2} - 4{R_1}+X_1^{\text{T}}A+{A^{\text{T}}}{X_1},\;\\[5pt] & {\Pi _{12}}{\rm{ = }}{P_1}X_1^{\text{T}}+{A^{\rm{T}}}{X_2}{\rm{+}}{P_1},\;{\Pi _{13}}{\rm{ = }} - 2{R_{\rm{1}}} - {P_{\rm{2}}}\\[5pt] & {\Pi _{16}}{\rm{ = }}{\tau _m}{P_3}+6{R_1},{\Pi _{22}}{\rm{ = }}\tau _m^2{R_1} +{{\rm{(}}{\eta _M} - {\tau _m})^2}{R_2}+X_2^{\text{T}} - {X_2},\;\\ & {\Pi _{33}}{\rm{ = }}{Q_3} - {Q_1} - 4{R_1} - {R_2},\;{\Pi _{44}}{\rm{ = }}S+{S^{\rm{T}}} - 2{R_2}\\[5pt] & {\Pi _{55}}{\rm{ = }} - {Q_{\rm{2}}} - {Q_{\rm{3}}} - {R_{\rm{2}}},\;{\vartheta _1}{\rm{ = }}e_1^{\text{T}}X_1^{\text{T}},\;{\vartheta _2}{\rm{ = }}e_2^{\text{T}}X_2^{\text{T}},\;\\[5pt] & {e_{\rm{1}}} = \left[ {I\;0\;0\;0\;0\;0\;} \right],\;{e_{\rm{2}}} = \left[ {0\;I\;0\;0\;0\;0\;} \right]{\text{。}} \end{split} $ | (11) |
证明:构造如下的 Lyapunov 泛函:
| $ V(t,{\xi _t})\; = {V_1}+{V_2}+{V_3}{\text{,}} $ | (12) |
其中,
| $ \begin{split} & \!\!\!\!\! {V_1}\!{\rm{ = }}\!{\xi ^{\rm{T}}}{\rm{(}}t){P_1}\xi {\rm{(}}t){\rm{ \!+\! }}2{\xi ^{\rm{T}}} \! \! {\rm{(}}t){P_2}\!\!\!\int_{{{t - }}{\tau _m}}^t {\xi {\rm{(}}s)} {\rm{d}} \! s{\rm{ \!+\! [\!\!}}\int_{{{t - }}{\tau _m}}^t {\xi {\rm{(}}s)} {\rm{d}} \! s{ \!\! ]^{\rm{T}}}\times \\[5pt] & {P_3}{\rm{[}}\int_{{{t - }}{\tau _m}}^t {\xi {\rm{(}}s)} {\rm{d}}s]{\text{,}}\\[5pt] & {V_{\rm{2}}}{\rm{ = }}\int_{t{\rm{ - }}{\tau _m}}^t {{\xi ^{\rm{T}}}{\rm{(}}s{\rm{)}}{Q_1}} \xi {\rm{(}}s){\rm{d}}s{\rm{+}}\int_{t{\rm{ - }}{\eta _M}}^t {{\xi ^{\rm{T}}}{\rm{(}}s{\rm{)}}{Q_2}} \xi {\rm{(}}s){\rm{d}}s{\rm{+}}\\[5pt] & \int_{t{\rm{ - }}{\eta _M}}^{t{\rm{ - }}{\tau _m}} {{\xi ^{\rm{T}}}{\rm{(}}s{\rm{)}}{Q_3}} \xi {\rm{(}}s){\rm{d}}s{\text{,}}\\[5pt] & {V_{\rm{3}}}{\rm{ = }}{\tau _m}\int_{{\rm{t - }}{\tau _m}}^t {\int_s^t {{{\dot \xi }^{\rm{T}}}} {\rm{(}}\theta {\rm{)}}{R_1}\dot \xi {\rm{(}}\theta ){\rm{d}}s} d\theta {\rm{+(}}{\eta _M} - {\tau _m})\\[5pt] & \int_{t{\rm{ - }}{\eta _M}}^{t{\rm{ - }}{\tau _m}} {\int_s^t {{{\dot \xi }^{\rm{T}}}{\rm{(}}\theta {\rm{)}}} {R_2}\dot \xi {\rm{(}}\theta ){\rm{d}}s} {\rm{d}}\theta{\text{。}} \end{split} $ | (13) |
对
| $ \begin{array}{l} {{\dot V}_1}{\rm{ = }}2{\xi ^{\rm{T}}}{\rm{(}}t){P_1}\dot \xi {\rm{(}}t)+2{{\dot \xi }^{\rm{T}}}{\rm{(}}t){P_2}\int_{t - {\tau _m}}^t {\xi {\rm{(}}s)} ds{\rm{+2}}{\xi ^{\rm{T}}}{\rm{(}}t)\times\\[5pt] \quad \quad {P_2}{\rm{[}}\xi {\rm{(}}t) - \xi {\rm{(}}t - {\tau _m}){\rm{]+2[}}\xi {\rm{(}}t) - \xi {\rm{(}}t - {\tau _m}){{\rm{]}}^{\rm{T}}}\times\\[5pt] \quad \quad {P_3}{\rm{[}}\int_{t - {\tau _m}}^t {\xi {\rm{(}}s)} {\rm{d}}s]{\text{,}}\\[5pt] {{\dot V}_2}{\rm{ = }}{\xi ^{\rm{T}}}{\rm{(}}t){\rm{(}}{Q_1}{\rm{+}}{Q_{\rm{2}}})\xi {\rm{(}}t) - \xi {{\rm{(}}t - {\tau _m})^{\rm{T}}}{\rm{(}}{Q_1} - {Q_3})\xi {\rm{(}}t - {\tau _m}) - \\[5pt] \quad \quad \xi {{\rm{(}}t - \eta {}_M)^{\rm{T}}}{\rm{(}}{Q_2}+{Q_3}{\rm{)}}\xi {\rm{(}}t - {\eta _M}){\text{,}}\\[5pt] {{\dot V}_3} = {{\dot \xi }^{\rm{T}}}{\rm{(}}t)\Theta \dot \xi {\rm{(}}t) - {\tau _{\rm{m}}}\int_{t - {\tau _m}}^t {{{\dot \xi }^{\rm{T}}}{\rm{(}}\theta )} {R_1}\dot \xi {\rm{(}}\theta ){\rm{d}}\theta - {\rm{(}}{\eta _M}{\rm{ - }}{\tau _{\rm{m}}})\\[5pt] \quad \quad\int_{{{t - }}{\eta _M}}^{t - {\tau _m}} {{{\dot \xi }^T}{\rm{(}}\theta {\rm{)}}{R_2}\dot \xi {\rm{(}}\theta ){\rm{d}}} \theta{\text{,}} \end{array} $ | (14) |
其中,
| $ \begin{split} \\[-12pt] & {\tau _m}\int_{t - {\tau _m}}^t {{{\dot \xi }^{\rm T}}{\rm{(}}\theta )} {R_1}\dot \xi {\rm{(}}\theta ){\rm d}\theta \leqslant - {{\rm{[}}\xi {\rm{(}}t{\rm{)}} - \xi {\rm{(}}t - {\tau _m}{\rm{)}}]^{\rm T}}{R_1}\\ & {\rm{[}}\xi {\rm{(}}t{\rm{)}} \!\!-\!\!\! \xi {\rm{(}}t \!\!-\!\! {\tau _m}{\rm{)}}] \!\!-\!\! {{\rm{[}}\xi {\rm{(}}t{\rm{) \!\!+\!\! }}\xi {\rm{(}}t \!\!-\!\! {\tau _m}{\rm{)}} \!\!-\!\! {\rm{(}}2/{\tau _m}) \int_{t \!\!-\!\! {\tau _m}}^t {\xi {\rm{(}}s){\rm d}s} ]^{\rm T}}\\ & {R_1}{\rm{[}}\xi {\rm{(}}t{\rm{)+}}\xi {\rm{(}}t - {\tau _m}{\rm{)}} - {\rm{(}}2/{\tau _m})\int_{t - {\tau _m}}^t {\xi {\rm{(}}s){\rm d}s} ]\text{。} \end{split} $ | (15) |
| $ \begin{split} \\[-12pt] & - {\rm{(}}{\eta _M} - {\tau _m})\int_{t - {\eta _M}}^{t - {\tau _m}} {{{\dot \xi }^{\rm T}}{\rm{(}}s)} {R_2}\dot \xi {\rm{(}}s)ds \leqslant - \\ & {{\rm{[}}\xi {\rm{(}}t \!-\! {\tau _m}{\rm{)}} \!-\! \xi {\rm{(}}t - \tau {\rm{(}}t{\rm{))}}]^{\rm T}}{{\rm{R}}_2}{\rm{[}}\xi {\rm{(}}t \!-\! {\tau _m}{\rm{)}} \!-\! \xi {\rm{(}}t - \tau {\rm{(}}t{\rm{))}}]+\\ & {\rm{ [}}\xi {\rm{(}}t - \tau {\rm{(}}t{\rm{))}} - \xi (t{\rm{ - }}{\eta _M}){]^{\rm T}}{{\rm{R}}_2}{\rm{[}}t - \tau {\rm{(}}t{\rm{)}} - \xi {\rm{(}}t - {\eta _M})]- \\ & {{\rm{[}}\xi {\rm{(}}t - {\tau _m}{\rm{)}} - \xi (t - \tau {\rm{(}}t{\rm{))}}]^{\rm T}}{\rm{S[}}t - \tau {\rm{(}}t{\rm{)}} - \xi {\rm{(}}t - {\eta _M})]+\\ & {{\rm{[}}\xi {\rm{(}}t \!-\! \tau {\rm{(}}t{\rm{))}} \!-\! \xi {\rm{(}}t \!-\! {\eta _M})]^{\rm T}}{S^T}{\rm{[}}\xi {\rm{(}}t \!-\! {\tau _{\rm{m}}}{\rm{)}} \!-\! \xi (t \!-\! \tau {\rm{(}}t{\rm{))}}]\text{。} \end{split} $ | (16) |
当系统未受到干扰时,ω(t)= 0,则存在任意适当维数的矩阵X1,X2 使得系统(6)满足如下等式:
| $ 2{\rm{(}}{\xi ^{\rm T}}{\rm{(}}t{\rm{)}}{ X}_1^{\rm T} \!\!+\!\! {\dot \xi ^{\rm T}}{\rm{(}}t){ X}_2^{\rm T}){\rm{(}}{ A}\xi {\rm{(}}t{\rm{) \!\!+\!\! }}{ B}K\xi {\rm{(}}t - \tau {\rm{(}}t{\rm{))}} \!\!-\!\! \dot \xi {\rm{(}}t)){\rm{ = }}0\text{,} $ | (17) |
则根据H∞ 性能定义及系统(6)得
| $ \dot V{\rm{(}}t){\rm{+}}{z^{\rm T}}{\rm{(}}t{\rm{)}}z{\rm{(}}t{\rm{)}} - {\gamma ^2}{\omega ^{\rm{T}}}{\rm{(}}t)\omega {\rm{(}}t{\rm{)}} \leqslant {\eta ^{\rm T}}{\rm{(}}t)\Xi \eta {\rm{(}}t)\text{,} $ | (18) |
其中,
| $\begin{split} \\[-12pt] \!\!\! \eta {\rm{(}}t){\rm{ \!\!=\!\! [}}\eta _1^{\rm T}{\rm{(}}t{\rm{) }}\eta _2^{\rm T}{{\rm{]}}^{\rm T}},{\eta _1}{\rm{(}}t){\rm{ =\!\! [}}{\xi ^{\rm T}}{\rm{(}}t{\rm{) }}{\dot \xi ^{\rm T}}{\rm{(}}t{\rm{) }}{\xi ^{\rm T}}{\rm{(}}t \!\!-\!\! {\tau _m}{\rm{) }}{{\rm{]}}^{\rm T}},{\eta _2}{\rm{(t}}) \!\!=\\[5pt] \quad \quad {\left[ {{\xi ^{\rm T}}{\rm{(}}t - \tau {\rm{(}}t{\rm{)) }}{\xi ^{\rm T}}{\rm{(}}t - {\eta _M}{\rm{) }}\frac{1}{{{\tau _m}}}\int_{t - {\tau _m}}^t {\xi {\rm{(}}s){\rm d}s} } \right]^{\rm T}}\text{。} \end{split} $ | (19) |
| $ \Xi {\rm{ = }}\left[ {\begin{array}{*{20}{c}} {{\Xi _{11}}} & {{\Xi _{12}}}\\ * & { - {\gamma ^2}I} \end{array}} \right]\text{。} $ | (20) |
当式(14):
本节基于系统(6)渐进稳定的充分条件设计航向控制器使无人艇航向控制系统镇定。
定理2:对于系统(6),给定标量τm,σca,τM,λ 及h,如果存在对称正定矩阵
| $ \left[ {\begin{array}{*{20}{c}} {{{\tilde P}_1}} & {{{\tilde P}_2}}\\ * & {{{\tilde P}_3}} \end{array}} \right] > 0 \text{,} $ | (21) |
| $ \left[ {\begin{array}{*{20}{c}} {{{\tilde R}_2}} & {\tilde S}\\ * & {{{\tilde R}_2}} \end{array}} \right] > 0 \text{,} $ | (22) |
| $ \left[ {\begin{array}{*{20}{c}} {{{\tilde \Xi }_{11}}} & {{{\tilde \Xi }_{12}}} & {{X^{\rm T}}{C^{\rm T}}}\\ * & {{\rm{ - }}{\gamma ^2}I} & 0\\ * & * & {{\rm{ - }}I} \end{array}} \right] \leqslant 0 \text{。} $ | (23) |
其中,
| $ \begin{array}{l} {{\tilde \Xi }_{11}}{\rm{ = }}\left[ \!\!\!\!\!\!\!\! {\begin{array}{*{20}{c}} {{{\tilde \Pi }_{11}}} & {{{\tilde \Pi }_{12}}} & {{{\tilde \Pi }_{13}}} & {B{\rm{W}}} & 0 & {{{\tilde \Pi }_{16}}}\\ * & {{{\tilde \Pi }_{22}}} & 0 & {\lambda B{\rm{W}}} & 0 & {{\tau _m}{{\tilde P}_2}}\\ * & * & {{{\tilde \Pi }_{33}}} & {{{\tilde \Pi }_{34}}} & {\tilde S} & {{{\tilde \Pi }_{36}}}\\ * & * & * & {{{\tilde \Pi }_{44}}} & {{{\tilde R}_2} - \tilde S} & 0\\ * & * & * & * & {{{\tilde \Pi }_{55}}} & 0\\ * & * & * & * & * & {{\rm{ - }}12{{\tilde R}_1}} \end{array}} \!\!\!\!\!\! \right],\\ {{\tilde \Pi }_{11}}{\rm{ = }}{{\tilde P}_2}+\tilde P_2^T+{{\tilde Q}_1}+{{\tilde Q}_2} - 4{{\tilde R}_1}+AX+X{A^T},\;\\[5pt] {{\tilde \Pi }_{12}}{\rm{ = }}{{\tilde P}_1} - X+\lambda {X^{\rm{T}}}{A^{\rm{T}}},\;\\[5pt] {{\tilde \Pi }_{13}}{\rm{ = }} - 2{{\tilde R}_1} - {{\tilde P}_{\rm{2}}},\;{{\tilde \Pi }_{16}}{\rm{ = }}{\tau _{\rm{m}}}{{\tilde P}_3}+6{{\tilde R}_1},\\[5pt] {{\tilde \Pi }_{22}}{\rm{\! =\! }}\tau _{\rm{m}}^2{{\tilde R}_1} \!\!+\!\! {\tau ^2}{{\tilde R}_2} \!\!-\!\! \lambda X{\rm{ \!+\! }}\lambda {X^T},\;{{\tilde \Pi }_{33}}{\rm{ \!=\! }}{{\tilde Q}_3} \!\!-\!\! {{\tilde Q}_1} \!-\! 4{{\tilde R}_1} \!-\! {{\tilde R}_2},\\[5pt] {{\tilde \Pi }_{34}}{\rm{ = }}{{\tilde R}_{\rm{2}}} - \tilde S,\;{{\tilde \Pi }_{36}}{\rm{ = }}6{{\tilde R}_1} - {\tau _m}{{\tilde P}_3},\;\tau {\rm{ = }}{\eta _M} - {\tau _m},\\[5pt] {{\tilde \Pi }_{44}}{\rm{ = }}\tilde S+{{\tilde S}^{\rm{T}}} - 2{{\tilde R}_2},{{\tilde \Pi }_{55}}{\rm{ = }} - {{\tilde Q}_{\rm{2}}} - {{\tilde Q}_{\rm{3}}} - {{\tilde R}_{\rm{2}}},\;\\[5pt] {{\tilde \Xi }_{12}}{\rm{ = }}e_1^{\rm T}E+e_2^{\rm T}\lambda E,\;{e_1} = \left[ {I\;0\;0\;0\;0\;0} \right],\;\\[5pt] {e_2} = \left[ {0\;I\;0\;0\;0\;0\;} \right]\text{。} \end{array} $ | (24) |
证明:由定理 1 知,系统(6)在满足式(7)~ 式(9)的条件下具有H∞ 性能范数界γ。令
定理 2 是在网络诱导时延下界τm ≠ 0 的情况下所设计的网络环境下无人水面艇的航向控制器。考虑τm = 0 时,无人艇航向控制器的设计。仍然运用式(10)的 Lyapunov 泛函,则可得定理 3。
定理3:对于系统(6),给标量τM、σca、λ 及h,如果存在对称正定矩阵
| $ \left[ {\begin{array}{*{20}{c}} {{{\tilde P}_1}} & {{{\tilde P}_2}}\\ * & {{{\tilde P}_3}} \end{array}} \right] > 0 \text{,} $ | (25) |
| $ \left[ {\begin{array}{*{20}{c}} {{{\tilde R}_2}} & {\tilde S}\\ * & {{{\tilde R}_2}} \end{array}} \right] > 0 \text{,} $ | (26) |
| $ \left[\!\!\!\! {\begin{array}{*{20}{c}} {{{\tilde \Pi }_{11}}} & {{{\tilde \Pi }_{12}}} & {{{\tilde \Pi }_{13}}} & {\tilde S} & {{{\tilde \Pi }_{15}}} & {{X^{\rm{T}}}{C^{\rm{T}}}}\\ * & {{{\tilde \Pi }_{22}}} & {\lambda BW} & 0 & 0 & 0\\ * & * & {{{\tilde \Pi }_{33}}} & {{{\tilde R}_2} - \tilde S} & 0 & 0\\ * & * & * & {{{\tilde Q}_2}+{{\tilde R}_2}} & 0 & 0\\ * & * & * & * & {{\gamma ^2}I} & 0\\ * & * & * & * & * & { - I} \end{array}} \!\!\!\!\! \right] \leqslant 0 \text{,} $ | (27) |
其中,
为了说明本文提出的算法和设计的航向控制器的有效性,取无人水面艇的前进速度U = 7.8 m/s,本文以某无人艇作为控制对象,根据文献[11]的参数得矩阵A,B,C,E 的值,即
| $ \begin{array}{l} { A} \!\!=\!\! \left[ \!\!\!\!{\begin{array}{*{20}{c}} {{\rm{ - }}0.1000}\!\! & \!\!0\!\! & \!\!0 \!\!& \!\!0 & \!\!0\\ {{\rm{ - }}0.2760} \!\!& \!\!{{\rm{ - }}0.6000} \!\!&\!\! 0 \!\!& \!\!0\!\! & \!\!0\\ 0 \!\!& \!\!1 \!\!& \!\!0\!\! &\!\! 0 \!\!& \!\!0\\ {0.6501} \!\!&\!\! 0\!\! & \!\!0 \!\!& { - 0.1180}\!\! &\!\! { - 0.3969}\\ 0 \!\!& \!\!0 \!\!&\!\! 0 \!\!&\!\! 1 \!\!& \!\!0 \end{array}} \!\!\!\!\right],\;\\ [5pt] { B} = {\left[ {0.00{\rm{78 }} - 0.0{\rm{126 }}0\; - 0.0{\rm{338 }}0} \right]^{\rm T}},\\[5pt] { C} \!\!=\!\! \left[ {0\;0{\rm{ 1 }}0\;0} \right], E \!\!= \!\!{\left[ {\begin{array}{*{20}{c}} 0 \!\!& \!\!0 \!\!& \!\!0 \!\!& \!\!{0.3969} \!\!& \!\!0\\ 0 \!\!& \!\!{0.6000} \!\!& \!\!0 \!\!& \!\!0 \!\!& \!\!0 \end{array}} \right]^{\rm T}}\text{。} \end{array} $ | (28) |
无人水面艇在航行中受海浪干扰采用ITTC单参数波普描述[17],即
| $ \begin{aligned} {G_{\omega \varphi }} = \frac{{0.02099s}}{{{s^2}+0.3637s+0.2675}},\\ {G_{\omega \psi }} = \frac{{0.2099s}}{{{s^2}+0.3637s+0.2675}}\text{。} \end{aligned} $ | (29) |
网络诱导时延和数据丢包参数如下:σca = 1,τm = 0.01,τM = 0.2,h = 0.1;并取λ = 0.2,则时变时延的曲线图如图 2 所示。
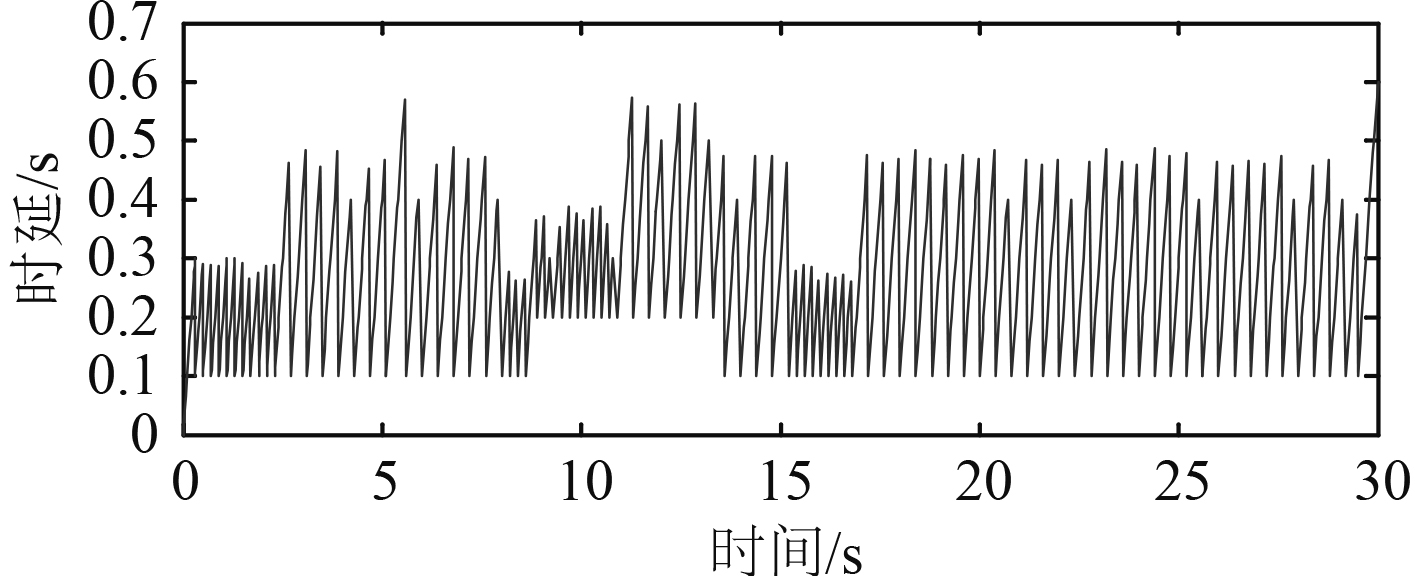
|
图 2 时变时延τ(t)的曲线图 Fig. 2 Curve of the interval time-varying delayτ(t) |
文献[13]和文献[16]提出了针对一般网络控制系统的控制方法。但文献[13]和文献[16]中的方法也可以处理本文所述的无人水面艇的航向控制器设计问题。在实验条件相同的前提下,采用文献[13]、文献[16]及本文提出的方法分别进行控制。初始值设为
|
|
表 1 无人艇航向控制H∞ 性能比较 Tab.1 TheH∞ performance comparison of USV heading control |
图 3 为相同网络诱导时延和数据丢包情况下,无人水面艇的航向保持控制曲线。从图中可看出,运用文献[13]、文献[16]的控制方法设计的无人艇航向控制器都使系统具有超调,且输出有振荡,达到稳定较慢。而本文设计的控制器响应速度快且无超调,能无静差地跟踪设定的航向。从图 3(b)也可看出,本文设计的控制器使舵角输出较为平滑,幅度较小。说明本文设计的控制器对无人艇航向保持控制具有较好的控制效果。
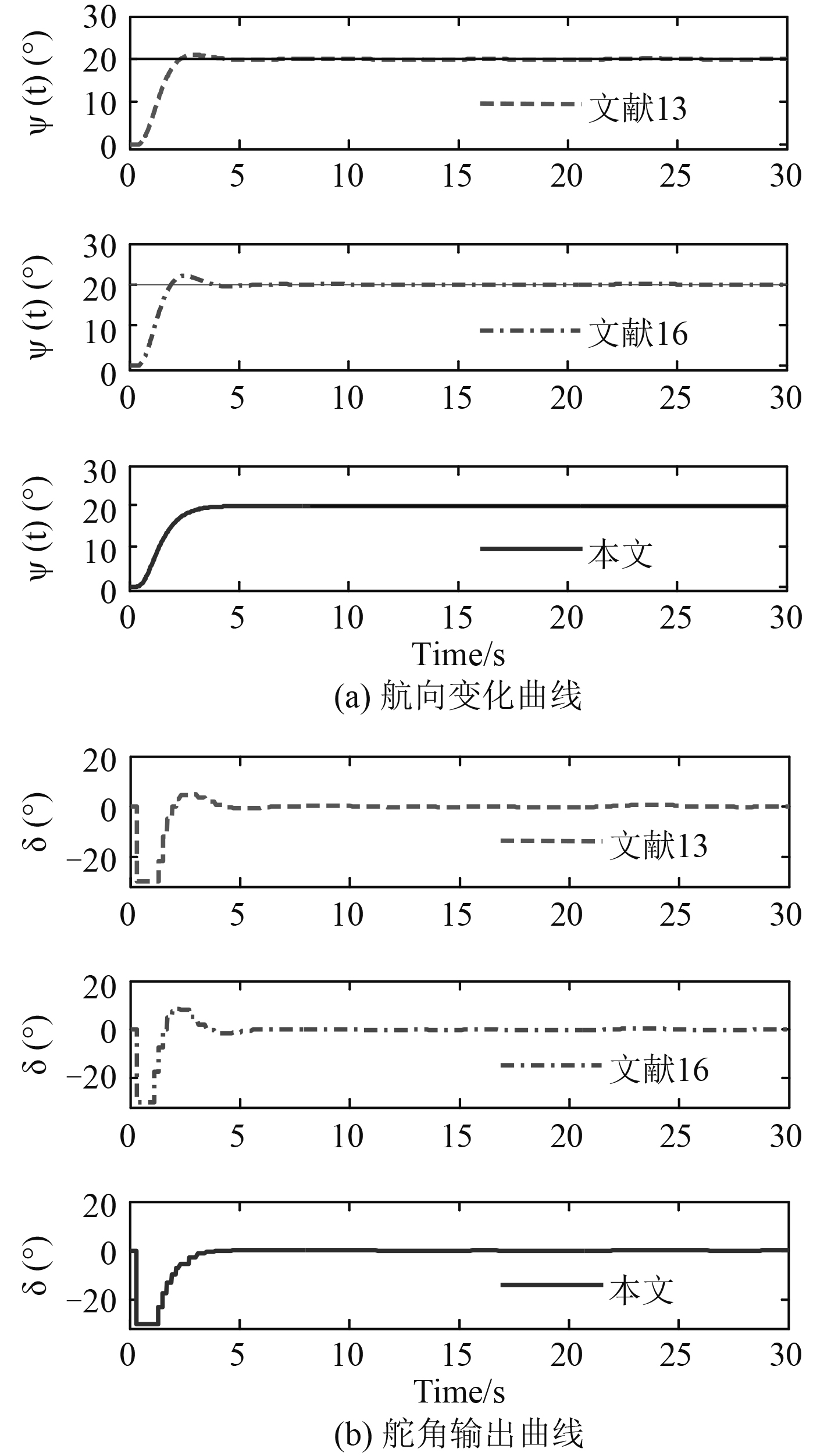
|
图 3 无人艇航向保持响应曲线 Fig. 3 The head-keeping response curves of USV |
从表 1 可看出,与应用文献[13]和文献[16]中的方法设计的无人水面艇的航向控制器相比,本文设计的控制器使系统达到稳定的时间最短为 2.94 s,且无超调,而文献[13]和文献[16]中的控制器,使无人艇航向控制系统都具有超调,且H∞ 性能范数界γ 都较本文的大,对外部的抗干扰性能较差。综上,本文设计的无人艇航向控制器,使系统达到稳定时间较短,无超调,无静差地跟踪设定的航向且对外部干扰具有较强的鲁棒性。
为了验证本文的航向控制策略对无人艇转向控制依旧有效,令期望的转向角ψd = 20°,采用上文控制器增益进行仿真。仿真结果见图 4。

|
图 4 无人艇航向转向响应曲线 Fig. 4 The head-turning response curves of USV |
图 4 为期望航向角为 20° 的无人艇航向转向响应曲线。从图 4可看出,由于存在网络诱导时延和数据丢包,航向变化曲线和控制舵角变化曲线都在约 0.3 s 时才开始响应,与应用文献[13]和文献[16]中的控制策略求出的无人艇航向控制器相比,本文设计的控制器能使无人艇快速地跟踪设定的航向,且无超调;图 4(b)也说明,本文设计的控制器使控制舵角较平滑的达到稳定,转向灵活,基本无超调。说明本文设计的控制器对网络环境下无人水面艇转向控制也具有较好的控制效果。
5 结语本文研究了网络环境下无人水面艇航向控制策略问题,在风、浪、流干扰下的模型基础上,建立基于网络的无人艇航向控制系统模型。基于 Lyapunov 稳定性条件和 LMI(线性矩阵不等式),得到使网络环境下无人水面艇航向控制系统的H∞ 性能判据。设计的航向控制器可使无人艇航向控制系统稳定,并且对外部干扰具有很强的鲁棒性,在无人艇航向控制领域,比文献[13]和文献[16]的控制性能更优。通过数值仿真,验证了算法的有效性。
| [1] | MAHACEK P, KITTS C A, MAS I. Dynamic guarding of marine assets through cluster control of automated surface vessel fleets[J]. IEEE/ASME. Transactions on Mechatronics . |
| [2] | SOHN S I, OH J H, LEE Y S, et al. Design of a fuel-cell-powered catamaran-type unmanned surface vehicle[J]. IEEE Journal of Oceanic Engineering, 2015, 2 (40): 388–396. |
| [3] | QI A C, HAN Q L, WANG Y L. A survey of motion control for marine vehicles[C]. Proceedings of the 34th Chinese Control Conference. Hangzhou, China, 2015:28-30. |
| [4] | YANG T C. Networked control system:a brief survey[J]. IEE Proc. Control Theory Applications . |
| [5] | HWANG K S, TAN S W, HSIAO M S, et al. Cooperative multi-agent congestion control for high speed networks[J]. IEEE Transactions on Systems Man and Cybemetics, 2005, 35 (2): 255–268. DOI: 10.1109/TSMCB.2004.842418 |
| [6] | KATAYAMA H, AOKI H. Straight-line trajectory tracking control for sampled-data underactuated ships[J]. IEEE Transactions on Control Systems Technology, 2014, 4 (22): 1638–1645. |
| [7] | 由丹丹, 廖煜雷, 董早鹏. 喷水推进无人艇航向的鲁棒S面控制方法[J]. 中南大学学报(自然科学版), 2013 (S1). |
| [8] | 王雨迪, 王国峰. 基于自抗扰控制算法的水面无人艇航向自动舵设计[D]. 大连:大连海事大学, 2014. |
| [9] | 廖煜雷, 庞杰光, 庄家园. 喷水推进型无人艇航向跟踪的反步自适应滑模控制[J]. 计算机应用研究, 2012 (1): 29. |
| [10] | 孙巧梅, 任光. 自适应逆控方法的无人艇航向控制[J]. 中国航海, 2012, 4 (35): 17–21. |
| [11] | 杨承恩, 贾星乐, 毕英君. 船舶舵阻摇及其鲁棒控制[M]. 大连: 大连海事大学出版社, 2001. |
| [12] | PENG C, FEI M R. An improved result on the stability of uncertain T-S fuzzy systems with interval time-varying delay[J]. Fuzzy Sets Syst, 2013, 212 (1): 97–109. |
| [13] | JIANG C, ZOU D X, ZHANG Q L. Observer-based control for networked control systems with network induced delay and packet dropout[C]. Proceedings of the 8th World Congress on Intelligent Control and Automation. Jinan, China, 2010, 4376-4379. |
| [14] | SEURET A, GOUAISBAUT F. Wirtinger-based integral inequality:application to time-delay systems[J]. Automatica, 2013, 49 (9): 2860–2866. DOI: 10.1016/j.automatica.2013.05.030 |
| [15] | WANG Y L, HAN Q L. Network-based fault detection filter and controller coordinated design for unmanned surface vehicles in network environments[J]. IEEE Transactions on Industrial Informatics, 2015 (c): 1551–3203. |
| [16] | 丰敏佳, 王玉龙. 连续时间网络控制系统的鲁棒故障检测[J]. 计算机工程, 2015, 8 (41): 101–109. |
| [17] | 刘胜. 现代船舶控制工程[M]. 北京: 科学出版社, 2010. |
| [18] | JIA X, ZHANG D, Hao X, et al. Fuzzy H∞ tracking control for nonlinear networked control systems in T-S fuzzy model[J]. IEEE Transcations on systems, Man and Cybernetics, 2009, 39 (4): 1073–1079. DOI: 10.1109/TSMCB.2008.2010524 |
 2017, Vol. 39
2017, Vol. 39
