2. 交通运输部北海航海保障中心天津航标处, 天津 300456
2. Tianjin Aid to Navigation Station, NGCN, MOT, Tianjin 300456, China
我国要实现向航运强国的目标,必须更加注重船舶操纵性是否能满足安全上的要求,这对国内学者关于船舶航行和操纵安全的研究提出了更严格的需求。近年来,全回转尾推进型拖轮(Azimuth Stern Drive Tug,ASD 拖轮),由于配备双导管桨,能在水平面内绕垂直轴 360° 旋转,操纵灵活、马力强劲、安全可靠,所以其功能任务具有多样性,在港口辅助操作、海洋平台拖航、安全救助等任务中,起到了不可或缺的主力军作用。国内外学者对其操纵运动特性进行了大量研究,尚未有理想的数学模型能适用于四象限全工况操纵运动的计算与仿真。
对培训拖轮驾驶员来说,仅依靠经验理论掌握操纵性还不够,全回转拖轮操纵模拟器[1] 对航海人才的教育培训、科学研究具有重要价值。在拖轮操纵模拟器环境中,存在大量静态或动态的障碍物,同样要求全回转导管桨工作在四象限,必要时须将桨偏角改变 180° 实现紧急停船。完整的数学模型能有效提高全回转拖轮模拟器的行为真实感[2]。仿真质量的提高,提高培训效率及成果的同时亦能节约资金投入。本文着重介绍一种新的导管桨四象限推力模型,同时提出的阻力模型能满足于全速域要求,最后通过 Visual Studio 2013 建立测试平台,开展一系列操纵性仿真试验[3] 研究,包括速度试航试验、螺旋线试验、Z 形试验[4]、回转试验和停船试验[5],覆盖了 ASD 拖轮运动从小桨偏角到大桨偏角,常速域到低速域的运动全程。
1 ASD 拖轮操纵运动数学模型假设 ASD 拖轮为刚体,在深、广、静、稳的水域中航行。ASD 拖轮运动采用定系
| $\left\{ {\begin{aligned} & {(m+{m_x})\dot u - (m+{m_y})vr = {X_H}{\rm{+}}{X_P}}\text{,}\\ & {(m+{m_y})\dot v+(m+{m_x})ur = {Y_H}+{Y_P}}\text{,}\\ & {({I_{zz}}+{J_{zz}})\dot r = {N_H}+{N_P}}\text{。} \end{aligned}} \right.$ | (1) |
式中:m,mx,my 为 ASD 拖轮质量在x 轴和y 轴的附加质量;Izz 为绕z 轴的质量惯性矩;Jzz 为附加质量惯性矩;u,v,r 为纵向、横向速度和回转角速度;XH,YH,NH 为船体水动力和首摇力矩;XP,YP,NP 为导管桨水动力和力矩。

|
图 1 ASD 拖轮水平面运动坐标系 Fig. 1 ASD tug horizontal plane coordinate system |
ASD 拖轮操纵运动的轨迹和姿态方程如下,运用四阶龙格-库塔法解算:
| $\left\{ {\begin{aligned} & {{{\dot x}_0} = u\cos \psi - v\sin \psi }\text{,}\\ & {{{\dot y}_0} = u\sin \psi+v\cos \psi }\text{,}\\ & {\dot \psi = r\cos \psi }\text{。} \end{aligned}} \right.$ | (2) |
其中:x0、y0 为位置坐标;Ψ 为航向。
2 拖船阻力模型 2.1 惯性力和粘性力流体惯性水动力的计算,参考周昭明关于附加质量mx、my 和附加质量惯性矩Jzz 的回归公式。井上模型在计算小漂角运动时的粘性水动力较理想:
| $\left\{ {\begin{aligned} & {{X_H} = X(u)+{X_{vv}}{v^2}+{X_{vr}}vr+{X_{rr}}{r^2}}\text{,}\\ & {{Y_H} = {Y_v}v+{Y_r}r+{Y_{|v|v}}|v|v+{Y_{|v|r}}|v|r+{Y_{|r|r}}|r|r}\text{,}\\ & {{N_H} = {N_v}v+{N_r}r+{N_{{\rm{|}}r|r}}|r|r+{N_{vvr}}{v^2}r+{N_{vrr}}v{r^2}}\text{。} \end{aligned}} \right.$ | (3) |
其中:“′”为 MMG 模型提出的一撇系统进行的无量纲化。关于水动力导数,采用井上公式计算线性项
其中纵向水动力导数的模型如下:
| ${X'_{{H}}} = X'(u')+{X'_{vv}}{v'^2}+{X'_{vr}}v'r'+{X'_{rr}}{r'^2}\text{。}$ | (4) |
其中:
ASD 拖轮直航阻力的计算采用二因次法:
| $X'(u') \!=\! {X'_{uu}}{u'^2} \!=\! - \frac{S}{{Ld}}{C_{\rm{t}}}{u'^2} \!=\! - \frac{S}{{Ld}}\left( {{C_{\rm{f}}} \!+\! {C_{\rm{r}}} \!+\! \Delta {C_{\rm{f}}}} \right){u'^2}\text{。}$ | (5) |
式中:S 为湿表面积;L 为船长;d 为吃水;Ct 为总阻力系数;Cf 为平板摩擦阻力系数;Cr 为剩余阻力系数;ΔCf 为粗糙度补贴系数。
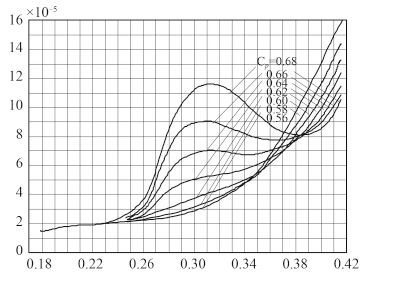
直航阻力计算的关键在于剩余阻力的确定。图 2 为塔格尔特拖轮剩余阻力图谱,专门用于拖轮剩余阻力系数的计算。
|
图 2 特格尔特拖轮剩余阻力曲线 Fig. 2 Target’s tug residual resistance curves |
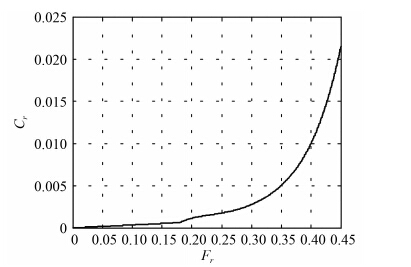
由图 2 可知,图谱在傅汝德数Fr 为 0~0.18(船速 0~5.6 kn)的范围内未给出曲线,Cr 与Fr 在Fr 为 0.18~0.25 之间已近似成线性关系,在 0~0.18 之间曲线曲率更小,为避免拟合时Cr 出现负值,对该段曲线作线性处理;在Fr 大于 0.18 时,采用 5 阶多项式拟合。最终的 ASD 拖轮剩余阻力系数图谱如图 3 所示,分段拟合后可用于计算机仿真,能适用于全速域条件下的 ASD 拖轮操纵运动要求。
|
图 3 ASD 拖轮塔格尔特剩余阻力曲线拟合 Fig. 3 ASD tug residual resistance curve fitting |
ASD 拖轮操纵运动时,2 个导管桨操作方向相同或相反,横向力及转矩大小相同,方向相同或相反。其联合推力模型如下:
| $\left\{ {\begin{aligned} & {{X_P} = {T_{(p)}}cos({\delta _{(p)}})+{T_{(s)}}cos({\delta _{(s)}})}\text{,}\\ & {{Y_P} = - {T_{(p)}}sin({\delta _{(p)}}) - {T_{(s)}}sin({\delta _{(s)}})}\text{,}\\ & {{N_P} \!=\! ({T_{(p)}}cos({\delta _{(p)}}) \!-\! {T_{(s)}}sin({\delta _{(s)}})) \cdot {L_{(ps)}}/2\! - \!\!{Y_P} \cdot {x_p}}\text{。} \end{aligned}} \right.$ | (6) |
式中:p 和s 分别为左右导管桨;
导管桨有导流管和螺旋桨 2 部分组成,性能优良。导管桨总推力系数
| $\left\{ {\begin{aligned} & {T = (1 - {t_{\rm{p}}})\rho {n^2}{D^4}{K_{\rm{T}}}(J)}\text{,}\\ & {J = (1 - {w_{\rm{p}}})u/(nD)}\text{,}\\ & {{K_T} = \sum {\sum {{A_{ij}}{{(H/D)}^i}{{(J)}^j}} } }\text{,}\\ & {{K_P} = \sum {\sum {{B_{ij}}{{(H/D)}^i}{{(J)}^j}} } }\text{,}\\ & {{K_{TN}} = \sum {\sum {{C_{ij}}{{(H/D)}^i}{{(J)}^j}} } }\text{。} \end{aligned}} \right.$ | (7) |
式中:ρ 为海水密度;n 为桨转速;D 为桨直径;J 为进速系数;
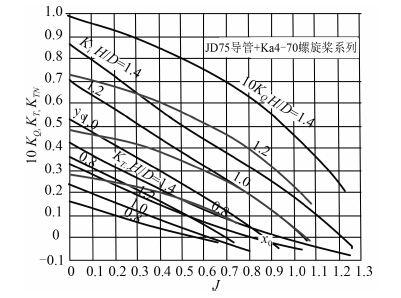
在简易导管桨图谱资料中,上海交大设计的 JD75+Ka 导管桨系列曲线形式直观,性能优良。本文以图 4 导管桨为原型(4 为桨叶数,70 为盘面比)。图 4 中x0,y0 为记下的特殊点坐标值。
|
图 4 JD75 导管+Ka4-70 螺旋桨系列正车敞水试验 Fig. 4 JD75 Ducted+Ka4-70 propeller’s open character curves |
有界形式的四象限螺旋桨工作特性图谱,突破了实际船舶四象限全工况表达上的困难,但未考虑带有导流管的情况。
| $\left\{ \begin{array}{l} P = (1 - {t_{\rm{p}}})\rho {D^2}({v_{\rm{P}}}^2+{n^2}{D^2}){K_{\rm{p}}}^\prime (J')\text{,}\\[5pt] {v_{{P}}} = (1 - {w_{\rm{P}}})u\text{,}\\[5pt] J' = {v_{\rm{P}}}/\sqrt {{v_{\rm{P}}}^2+{n^2}{D^2}} = \left\{ \begin{array}{l} J\sqrt {1+{J^2}} ;\;\;\;\;n > 0{\rm{ }}\text{,}\\ - J/\sqrt {1+{J^2}} ;\;n < 0{\rm{ }}\text{,} \end{array} \right.\\[5pt] {K_{{p}}}^\prime (J') = P/\rho {D^2}({v_{{P}}}^2+{n^2}{D^2}) = {K_{{p}}}/1+{J^2}\text{。} \end{array} \right.$ | (8) |
式中:
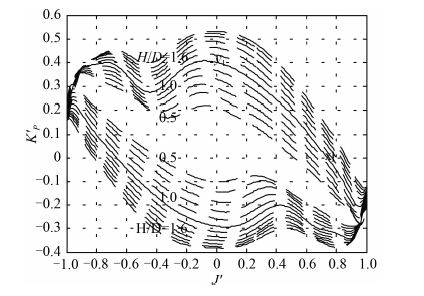
在四象限螺旋桨推力图谱[7] 资料中,哥德堡水池试验得出的诺尔特斯特洛姆[8]Nordstrom 系列应用广泛。该图谱适合螺距比
|
图 5
四象限螺旋桨推力 |
对图 4 用到的的推力曲线
| ${x^\prime } = x/\sqrt {1+{x^2}} ;{y^\prime } = y/1+{x^2}\text{,}$ | (9) |
则处理后得出如图 6 中的
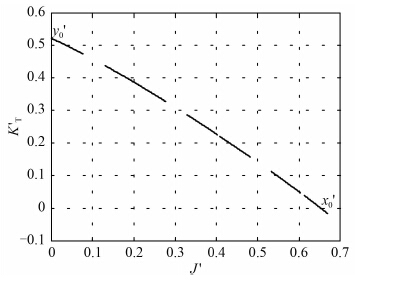
|
图 6
导管桨第一象限 |
对图 5 用到的
| $\left\{ \begin{array}{l} \!\!\!\! a = {{y'}_0}/{y_1}\text{,}\\ \!\!\!\! {b_1} = {{x'}_0}/{x_1};\;\;\;\;\;\;\;\;\;\;\;{b_2} = \left( {1 - {{x'}_0}} \right)/\left( {1 - {x_1}} \right)\text{,}\\[5pt] \!\!\!\! n > 0,{\rm{ }}0 \leqslant J' < {x_1}{\rm{;}}\;\;x' = {b_1}x,{\rm{ }}y' = ay\text{,}\\[5pt] \!\!\!\! n \!\!> \!\!0,{\rm{ }}{x_1} \leqslant J'\!\! \leqslant \!\!1;\;\;\;x' \!\!=\!\! {{x'}_0}+{b_2}(x - {x_1}),{\rm{ }}y' \!\!=\!\! ay\text{,}\\[5pt] \!\!\!\! n > 0, - 1 \leqslant J' < 0;\;\;x' = x,{\rm{ }}y' = ay\text{,}\\[5pt] \!\!\!\! n < 0, - 1 \leqslant J' \leqslant 1;\;\;x' = x,{\rm{ }}y' = ay\text{。} \end{array} \right.$ | (10) |
则处理后得出图 7 中的第二、三和四象限推力曲线
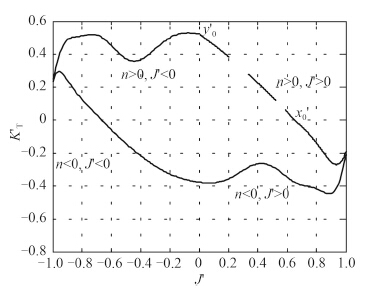
|
图 7
导管桨四象限推力 |
式(11)为最终的导管桨四象限推力系数计算模型。该模型既考虑了导流管的作用,又符合四象限全工况实际工作特性;既避免了仿真严重失真,又突出了定常正倒车之间、正车到倒车与倒车到正车过程的不对称性。
| $T = (1 - {t_{{p}}})\rho {D^2}({v_{{P}}}^2+{n^2}{D^2}){K_{{T}}}^\prime (J')\text{。}$ | (11) |
表 1 为船桨参数。仿真对比资料是从丹麦 Force Technology 公司购买的全回转拖轮运动数学模型时配套提供的试验数据(记为 DMI 数据),但模型内部结构和参数看不到,原型船为 ASD 拖轮 Delta Linda。
|
|
表 1 Delta Linda 拖轮船桨参数 Tab.1 Delta Linda tug parameters |
图 8为使用 Visual Studio 2013 软件构建的 Modeler 仿真平台,其既能实时显示船舶的位置、航向及速度信息,又能对指定数据在指定时间段内进行存取。
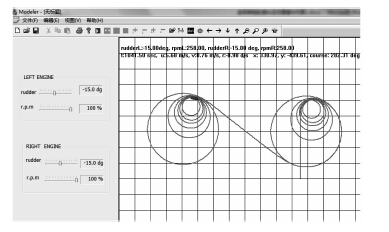
|
图 8 Modeler 仿真测试平台 Fig. 8 Modeler simulation platform |
表 2 显示误差值最大为 4.7%,仿真效果良好,证明该模型在直航状态下较为理想。
|
|
表 2 速度试航和仿真结果 Tab.2 Speed trial test simulation results |
从螺线试验可看出各桨偏角下的定常回转角速度r,船舶是否直线稳定以及稳定性的好坏,不具有直线稳定性船舶的不稳定程度等操纵性能。如图 8其试验运动轨迹形如螺线。试验步骤:先让拖船保持匀速直航,调整桨偏角
图 9 为 DMI 数据与仿真数据得出的r-
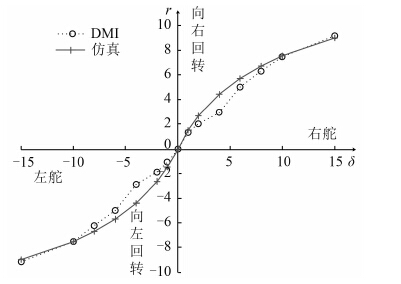
|
图 9 螺线试验 Fig. 9 Spiral test |
表 3 显示了螺线试验回转速降对比情况,DMI 数据与仿真数据最大误差为 3.3%,精度较高。两者桨偏角越大,漂角越大,纵向速度降幅越大,回转半径越小。进一步表明了 ASD 拖轮回转性能的优良,当受到环境干扰时,为保持航向,需要及时调整桨偏角,调整后又过于灵敏,与拖船操作实况相符。
|
|
表 3 螺线试验回转速降 Tab.3 Spiral test speed loss |
利用 Z 形试验结果可以计算操纵性指数,易于判别船舶操纵性能,特别是中、小桨偏角下保持和改变航向的能力。10° Z 形试验步骤:先让拖船保持匀速直航,尽快将桨偏角调至左 10°;当首向角左偏初始航向 10°时,立刻将桨偏角调至右 10°,记为第 2 次操作;当首向角右偏离初始航向 10°时,再向左操作;如此来回操作 5 次结束试验。20° Z 形试验同上,将桨偏角每次改为 20°即可。
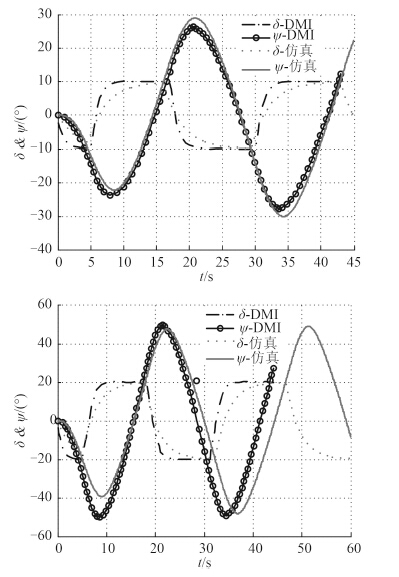
图 10 分别给出了 10°和 20° Z 形试验的桨偏角和首向角的历时曲线。可看出,2 个 Z 形试验仿真数据与 DMI 实船数据变化基本一致,误差在合理范围内。其中,10°较 20°准确,后者较前者执行桨偏角稍有延迟。另外,执行桨偏角越大,首向角向左右舷各摆动一次的周期越大,拖船运动越偏离中心线,在实际操船中 10°桨偏角也更常用。在 10°Z 形试验图中,ASD 拖轮仿真计算的第一、第二超越角分别为 14.1°和 19.0°,第一、第二超越时间分别为 4.0s 和 4.8s,周期为 27.8s;相对应的 DMI 数据为 13.8°和 15.7°,3.0s 和 4.0s,周期为 27.7s。普通船舶超越角在 10°左右,该 ASD 拖轮超越角较大,表明其回转性良好,跟从性一般。
|
图 10 Z 形试验 Fig. 10 Zigzag test |
旋回性能代表了船舶航向改变的能力。ASD 拖轮作旋回运动时,先直航前进,改变桨偏角并稳定,拖轮重心运动的轨迹称为旋回圈,其特征参数为判别 ASD 拖轮旋回性能好坏提供了依据。
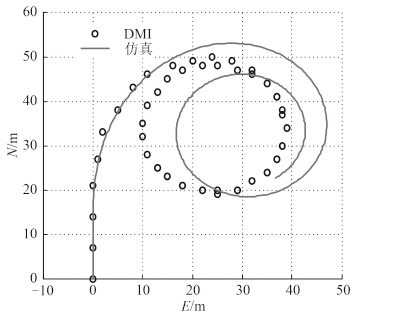
旋回运动轨迹如图 11 所示。本次试验初始航向为正北,初始航速为 13.61kn,将桨偏角均向右偏 35°操作。相应特征参数的对比结果如表 4。
|
图 11 35°回转试验 Fig. 11 35° turning test |
|
|
表 4 旋回圈参数对比 Tab.4 Turning circle parameters comparison |
从图 11 和表 4 可知,完成旋回运动纵向和横向占用水域距离均小于 2 倍拖轮船长,体现了 ASD 拖轮优良的旋回性能。由表 4 对比数据可知,旋回初径的误差值最大,仍在合理范围内。
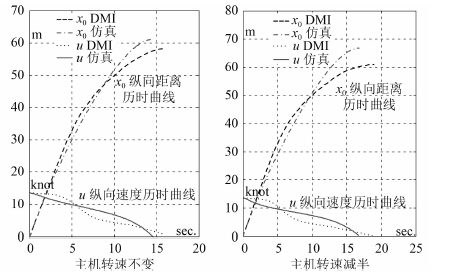
4.5 停船试验普通单桨船倒车停船时,螺旋桨旋转方向改变,航迹不是直线,沿曲线轨迹作偏转运动。ASD 拖轮的倒车停船操纵有所差异,其在倒车停船时,螺旋桨旋转方向不变,把桨偏角改变 180°,航迹为“1”字直线型。下令停船到 ASD 拖轮船速为降为 0 时船舶纵向前进的距离,即为停船冲程。DMI 数据给出的倒车停船试验,在桨偏角旋转 180°的同时,分为主机转速不变和主机转速减半 2 种情况。仿真时采取完全相同的初始条件,图 12 给出了纵向距离历时曲线x0 和纵向速度历时曲线u 的对比情况。
|
图 12 停船试验 Fig. 12 Stopping test |
从图 12 可知,在主机转速不变的条件下,停船冲程 DMI 数据为 58.4 m,仿真数据为 61.1 m,误差为 4.6%;停船冲时 DMI 数据为 16.0 s,仿真数据为 14.6 s,误差为 8.8%。在主机转速由全速变为半速的条件下,停船冲程 DMI 数据为 61.1 m,仿真数据为 66.8 m,误差为 9.3%;停船冲时 DMI 数据为 18.9 s,仿真数据为 16.8 s,误差为 11.1%。图中 DMI 与仿真纵向距离历时曲线变化趋势相当一致;纵向速度历时曲线对比中,DMI 数据与仿真数据变化趋势略有不同,两导管桨相对位置不同,干扰会有变化,表示该模型在两桨干扰方面有待改进。总体来看,2 组试验中的衡准参数误差均在可接受范围内,特别是左图 ASD 拖轮紧急停船的运动过程,一致性良好,进一步表明了所建模型的有效性。
5 结 语基于操纵性理论和分离型建模思想,本文给出了 ASD 拖轮适用于全工况操纵运动的数学模型及其仿真平台。通过对 ASD 拖轮进行速度试航试验,表明该模型在常速域直航状态下的精度较高;通过螺旋线试验、Z 形试验和回转试验,体现了该模型具有保持和改变航向的能力;通过停船试验,验证了该模型从常速域到低速域均满足推阻力匹配要求。综上,本文所建船舶运动数学模型正确有效,对全回转拖轮操纵模拟器的开发与完善具有参考意义。
| [1] |
陈宁, 王之民, 李雯, 等. 全回转拖轮运动建模与视景仿真[J]. 舰船科学技术, 2015, 37 (8): 52–56.
CHEN Ning, WANG Zhi-min, LI Wen, et al. Research on the turning movement and visual simulation for the Z-propeller tug[J]. Ship Science and Technology, 2015, 37 (8): 52–56. |
| [2] |
尹勇, 金一丞, 任鸿翔, 等. 全任务航海仿真系统的评价方法及关键技术研究[J]. 系统仿真学报, 2009, 21 (21): 6910–6914.
YIN Yong, JIN Yi-cheng, REN Hong-xiang, et al. Research on evaluation method and key technologies of full mission navigation simulation system[J]. Journal of System Simulation, 2009, 21 (21): 6910–6914. |
| [3] |
李秋珍, 刘畅. 船舶操纵性评估体系构架设计[J]. 舰船电子工程, 2012 (12): 101–103, 135.
LI Qiu-zhen, LIU Chang. Design of evaluation arctitecture on the ship's maneuverability[J]. Ship Electronic Engineering, 2012 (12): 101–103, 135. |
| [4] |
洪碧光, 赵发明, 孔庆文, 等. 船舶Z形操纵试验的数值模拟[J]. 大连海事大学学报, 2015, 41 (2): 1–6.
HONG Bi-guang, ZHAO Fa-ming, KONG Qing-wen, et al. Numerical simulation of ship's zigzag test[J]. Journal of Dalian Maritime University, 2015, 41 (2): 1–6. |
| [5] |
陆冬青. 船舶倒车停船运动仿真研究[J]. 舰船科学技术, 2007, 29 (4): 110–113.
LU Dong-qing. Simulation on ship stopping motion by reverse propulsion[J]. Ship Science and Technology, 2007, 29 (4): 110–113. |
| [6] | 霍虎伟. 航海模拟器中全回转拖轮操纵运动建模与仿真[D]. 大连:大连海事大学, 2013. |
| [7] |
李殿璞. 基于螺旋桨特性四象限Chebyshev拟合式的深潜艇正倒航变速推进模型[J]. 哈尔滨工程大学学报, 2002, 23 (1): 52–57.
LI Dian-pu. Chebyshev fit of propeller properties across four quadrants and propulsion model of DSV[J]. Journal of Harbin Engineering University, 2002, 23 (1): 52–57. |
| [8] | LI Dian-pu, WANG Zhong-yi, CHI hai-hong. Chebyshev fitting way and error analysis for propeller atlas across four quadrants[J]. Journal of Marine Science and Application, 2002, 1 (1): 52–59. DOI: 10.1007/BF02921417 |
| [9] | YE Bao-yu, WANG Qin-ruo, WAN Jia-fu, et al. A four-quadrant thrust estimation scheme based on chebyshev fit and experiment of ship model[J]. Open Mechanical Engineering Journal, 2012, 6 (1): 148–154. DOI: 10.2174/1874155X01206010148 |
 2017, Vol. 39
2017, Vol. 39
