0 引言

随着海洋事业的不断发展，人们对海洋开发和探索逐渐向深海扩展，在海洋工程设施建设中，船舶海上作业已经成为了不可或缺的重要部分。由于海洋环境的复杂性，对船舶动力定位系统的精度越来越严苛。为了增强系统的鲁棒性，近几年一些鲁棒性较强的混沌控制方法被提出，包括线性反馈控制^[1]、La Salle 不变集控制、Laypunov 指数控制、自适应模糊控制、支持向量机控制、有限时间控制、滑模控制等^[2]。其中，滑模变结构控制^[3]（sliding mode control，SMC）不依赖于具体的数学模型，具有较强的鲁棒性，但存在一定的抖振问题，影响了实际应用。近年来，提出很多改进的滑模控制方法，如自适应滑模、模糊滑模、神经网络滑模^[4]等。以上控制方法虽然能够在不同程度上降低抖振，提高被控系统的鲁棒性，但均要求系统的所有状态完全可测。因此，当系统部分状态无法被精确测量时，上述控制方法将会失效。扩张状态观测器（Extended State Observer，ESO）^[5]是韩京清提出的自抗扰控制技术中的重要组成部分，能观测系统的未知状态和不确定项。该方法对系统模型敏感度较低，且对非线性扰动具有较强的鲁棒性，因此在很多领域得到了广泛应用。

本文针对海洋平台船舶动力定位控制系统，结合反演滑模控制与扩张观测器的优势，提出一种基于扩张观测器的船舶动力定位反演滑模控制方法，取消了系统所有状态完全可测的限制。利用 ESO 估计动力定位控制系统的未知状态及不确定项，克服系统中的非线性环节和参数不确定性的影响，同时设计反演滑模控制器，提高控制性能且有效地抑制传统滑模控制的抖振问题。

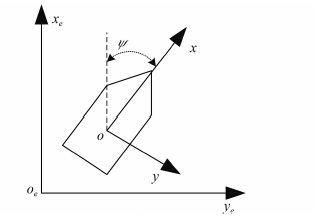
1 船舶数学模型

在船舶动力定位系统研究过程中，一般只考虑 3 个自由度，即横荡、纵荡和首摇。同时，系统建模一般还需要 2 个坐标系。一个是相对地球固定的大地坐标系x_eo_ey_e；另一个是相对船舶建立的船体坐标系xoy^[6-7]。如图 1 所示。

其中，2 种坐标系之间的转换关系和低频运动模型如下：

$ \left\{ \begin{array}{l} \dot \eta = R\left( \psi \right)v \text{，}\\ M\dot \nu+D\nu = {R^{\rm T}}(\psi )b+\tau \text{。} \end{array} \right. $

(1)

式中：${{\eta }} = {[x,y,\psi ]^{\rm T}}$ 为大地坐标系下船舶的位置向量；${{v}} = {[u,\upsilon ,r]^{\rm{T}}}$ 为在随船坐标系下船舶的速度向量；b 为环境扰动力；τ 为控制量。R（Ψ）为两坐标系之间的转换矩阵，M 为质量矩阵，D 称为阻尼系数矩阵，分别为：

$ \begin{array}{l} { R}(\psi ) = \left[ {\begin{array}{*{20}{l}} {\cos \psi } & { - \sin \psi } & 0\\ {\sin \psi } & {\cos \psi } & 0\\ 0 & 0 & 1 \end{array}} \right]\text{，}\\ { M} = \left[ {\begin{array}{*{20}{c}} {m - {X_{\dot u}}} & 0 & 0\\ 0 & {m - {Y_{\dot v}}} & {m{x_g} - {Y_{\dot r}}}\\ 0 & {m{x_g} - {N_{\dot v}}} & {{I_z} - {N_{\dot r}}} \end{array}} \right]\text{，}\\ { D} = \left[ {\begin{array}{*{20}{c}} { - {X_u}} & 0 & 0\\ 0 & { - {Y_v}} & { - {Y_r}}\\ 0 & { - {N_v}} & { - {N_r}} \end{array}} \right]\text{。} \end{array} $

式中，m 为船舶总质量；x_g 为船舶中心和重心之间的距离，一般取x_g ≈ 0；I_z 为转动惯性矩阵；X_u，Y_v，Y_r，N_v，N_r 均是水动力系数；${X_{\dot u}}$，${Y_{\dot v}}$，${N_{\dot r}}$，${Y_{\dot r}}$，${N_{\dot v}}$ 均为附加质量系数。

2 基于扩张观测器的反演滑模变结构控制系统的设计

考虑到船舶在动力定位过程中，控制系统系统存在未知外部干扰以及船舶模型参数不确定性的问题，将系统分为内环观测器和外环控制器分别设计。利用扩张状态观测器将系统模型不确定性影响和外部干扰组成的复合扰动相对准确地估计出来，并在反演滑模控制器中进行补偿。

2.1 扩张观测器的设计

扩张观测器是一种非线性状态观测器，对系统模型敏感度较低，是自抗扰控制的重要组成部分。ESO 可以估计出船舶动力定位控制系统中的未知外部干扰以及船舶模型参数不确定性，并进行补偿，使系统的抗干扰性加强^[5]。

设一个带有未知扰动的非线性不确定系统为：

$ \left\{ \begin{array}{l} {x^{\left( n \right)}} = f\left( {x,{x^{\left( 1 \right)}}, \cdots ,{x^{\left( {n - 1} \right)}},t} \right)+w\left( t \right)+bu \text{，}\\ y = x\left( t \right)\text{。} \end{array} \right. $

(2)

式中：$f\left( {x,{x^{\left( 1 \right)}}, \cdots ,{x^{\left( {n - 1} \right)}},t} \right)$ 为未知函数；w（t）为未知扰动；x（t）为系统状态变量；u 为系统控制量；b 控制量增益。

设 $a\left( t \right) = f\left( {x,{x^{\left( 1 \right)}}, \cdots ,{x^{\left( {n - 1} \right)}},t} \right)+w\left( t \right)$，则n+1 阶 ESO 的一般形式为：

$ \left\{ \begin{array}{l} {{\dot z}_1} = {z_2} - {g_1}\left( {{z_1} - x\left( t \right)} \right)\text{，}\\ \vdots \\ {{\dot z}_n} = {z_{n+1}} - {g_n}\left( {{z_1} - x\left( t \right)} \right)+bu \text{，}\\ {{\dot z}_{n+1}} = - {g_{n+1}}\left( {{z_1} - x\left( t \right)} \right)\text{。} \end{array} \right. $

(3)

式中：${z_1} \to x\left( t \right), \cdots {z_n} \to {x^{n - 1}}\left( t \right),{z_{n+1}} \to a\left( t \right)$ 为对未知函数 $f\left( {x,{x^{\left( 1 \right)}}, \cdots ,{x^{\left( {n - 1} \right)}},t} \right)$ 和扰动w（t）的估计；g_i（·）为非线性函数，一般取如下形式：

$ \begin{array}{l} fal\left( {\varepsilon ,\alpha ,\delta } \right) = \left\{ \begin{array}{l} {\left| \varepsilon \right|^\alpha }sat\left( \varepsilon \right),\left| \varepsilon \right| > \delta \text{，}\\ sign\left( \varepsilon \right),\varepsilon \leqslant \delta \text{，} \end{array} \right.\\ sat\left( \varepsilon \right) = \left\{ \begin{array}{l} \varepsilon /\varsigma ,\left| \varepsilon \right| \leqslant \varsigma \text{，}\\ sign\left( \varepsilon \right),\left| \varepsilon \right| > \varsigma \text{。} \end{array} \right. \end{array} $

(4)

由式（1）可推出，对应船舶动力定位系统数学模型的 ESO 形式为：

$ \left\{ \begin{array}{l} {{\dot z}_1} = {z_2} - {\beta _1}{\varepsilon _1}\text{，}\\ {{\dot z}_2} = {z_3} - {\beta _2}fal\left( {{\varepsilon _1},{\alpha _1},\delta } \right)+bu\text{，}\\ {{\dot z}_2} = - {\beta _3}fal\left( {{\varepsilon _1},{\alpha _2},\delta } \right)\text{。} \end{array} \right. $

(5)

式中：β₁，β₂，β₃ ＞ 0 为观测器系数；α₁，α₂，α₃ 为非线性因子，通常情况下取α₁ = 1，α₂ = 0.5，α₃ = 0.25；δ 为滤波因子。

由式（5）可看出，非线性函数fal（·）产生的增益与系统观测误差ε₁ 成反比例关系，即ε₁ 较大时，产生的增益较小，而ε₁ 较小时，产生的增益则较大。从文献[6]可知，参数β_i 只要选择合适，fal（·）函数可以保证观测器状态z_i→x_i，i = 1，2，3。即观测误差可以收敛到 $\left| {{x_i} - {z_i}} \right| \leqslant {d_i}$，其中d_i ＞ 0 是一个很小的正数。

2.2 反演滑模控制器的设计

对于二阶动力学系统而言，在相平面上，当状态轨迹在滑动模态面外时，滑模变结构的开关控制会迫使其向滑模面运动。当到达滑模面后，运动点会沿着滑模面到达状态稳定点，并且不受外界环境的干扰，鲁棒性较高。结合 back-stepping 思想和滑模控制的优势，在动力定位控制系统的外环控制器中，利用反演滑模控制使整个闭环系统满足期望的动态与静态性能指标^[9]。

将式（1）进行整理：

$ { M}{{ R}^{ - 1}}\left( \varphi \right)\ddot \eta+{ M}{\dot { R}^{ - 1}}\left( \varphi \right)\dot \eta+{ D}{{ R}^{ - 1}}\left( \varphi \right)\dot \eta = \tau+d\left( t \right)\text{，} $

(6)

为了设计的方便，将式（6）进行改写：

$ \ddot \eta = { A}\dot \eta+{ B}\left( {\tau+d\left( t \right)} \right)\text{，} $

(7)

式中：${ A} \,\,=\, \,-\, { R}\left( \varphi \right){\dot { R}^{ - 1}}\!\left( \varphi \right) \,\,-\,\, { R}\left( \varphi \right){{ M}^{ - 1}}{ D}{{ R}^{ - 1}}\left( \varphi \right)$, ${ B} \,\,=\,\, $ $ { R}\left( \varphi \right){{ M}^{ - 1}}$。

设 ${v^*} \!=\! { R}\left( \varphi \right)v \Rightarrow \dot \eta \!=\! {v^*}$，对式（1）进行简单调整：

$ \left\{ \begin{array}{l} \dot \eta = {v^*}\text{，}\\ {{\dot v}^*} = { A}{v^*}+{ B}\left( {\tau+d\left( t \right)} \right)\text{。} \end{array} \right. $

(8)

控制器设计步骤如下：

1） 船舶轨迹跟踪误差为z₁ =η-η_d，η_d 为船舶目标位置，则 ${\dot z_1} = {v^*} - {\dot \eta _d}$。

定义 Lyapunov 函数：

$ {V_1} = \frac{1}{2}z_1^2\text{，} $

(9)

定义 ${v^*} = {z_2}+{\dot \eta _d} - {c_1}{z_1}$，其中c₁ 为正的常数，z₂ 为虚拟控制项，${z_2} \!=\! {v^*} \!-\! {\dot \eta _d} \!+\! {c_1}{z_1}$，则 ${\dot z_1} \!=\! {x_2} \!-\! {\dot x_d} \!=\! {z_2} \!-\! {c_1}{z_1}$，且

$ {\dot V_1} = {z_1}{\dot z_1} = {z_1}{z_2} - {c_1}z_1^2\text{，} $

(10)

定义切换函数为：

$ \sigma = {k_1}{z_1}+{z_2}\text{。} $

(11)

其中k₁ ＞ 0。

由于 ${\dot z_1} = {z_2} - {c_1}{z_1}$，则

$ \sigma \!=\! {k_1}{z_1} \!+\! {z_2} \!=\! {k_1}{z_1} \!+\! {\dot z_1}+{c_1}{z_1} = \left( {{k_1}+{c_1}} \right){z_1}+{\dot z_1}\text{。} $

(12)

由于k₁ +c₁ ＞ 0，显然，如果σ = 0，则z₁ = 0，z₂ = 0 且 ${\dot V_1} \leqslant 0$。为此。需要下一步设计。

2） 定义 Lyapunov 函数：

$ {V_2} = {V_1}+\frac{1}{2}{\sigma ^2}\text{，} $

(13)

则

$ \begin{split}\\[-12pt] {{\dot V}_2} = & {{\dot V}_1}+\sigma \dot \sigma = {z_1}{z_2} - {c_1}z_1^2+\sigma \dot \sigma = \\ & {z_1}{z_2} - {c_1}z_1^2+\sigma \left( {{k_1}{{\dot z}_1}+{{\dot z}_2}} \right) = \\ & {z_1}{z_2} \!-\! {c_1}z_1^2 \!+\! \sigma \left( {{k_1}\left( {{z_2} \!-\! {c_1}{z_1}} \right) \!+\! {v^*} \!-\! {{\ddot \eta }_d} \!+\! {c_1}{{\dot z}_1}} \right) = \\ & {z_1}{z_2}\! - \!{c_1}z_1^2 \!+\! \sigma \left( {{k_1}\left( {{z_2} \!-\! {c_1}{z_1}} \right) \!+\! A\left( {{z_2} \!+\! {{\dot \eta }_d} \!-\! {c_1}{z_1}} \right)} +\right.\\ & \left. { Bu+F - {{\ddot \eta }_d}+{c_1}{{\dot z}_1}} \right)\text{。} \end{split} $

(14)

设计控制器为：

$ \begin{split}\\[-12pt] u = & {{ B}^{ - 1}}\left( { - {k_1}\left( {{z_2} - {c_1}{z_1}} \right) - A\left( {{z_2}+{{\dot \eta }_d} - {c_1}{z_1}} \right) - } \right.\\ & \left. {\bar F{\mathop{\rm sgn}} \left( \sigma \right)+{{\ddot \eta }_d} - {c_1}{{\dot z}_1} - h\left( {\sigma+\beta {\mathop{\rm sgn}} \left( \sigma \right)} \right)} \right)\text{。} \end{split} $

(15)

其中h 和β 为正的常数。

3 系统稳定性分析

现假设系统的 ESO 的参数选择合适，使得误差收敛到 0。将式（15）代入式（14）可得：

$ \begin{split}\\[-12pt] {{\dot V}_2} = & {z_1}{z_2} - {c_1}z_1^2 - h{\sigma ^2} - h\beta \left| \sigma \right|+F\sigma - \\ & \bar F\left| \sigma \right| \leqslant - {c_1}z_1^2+{z_1}{z_2} - h{\sigma ^2} - h\beta \left| \sigma \right|\text{，} \end{split} $

(16)

取

$ { Q} = \left[ {\begin{array}{*{20}{c}} {{c_1}+hk_1^2} & {h{k_1} - \frac{1}{2}}\\ {h{k_1} - \frac{1}{2}} & h \end{array}} \right]\text{，} $

(17)

由于

$ \begin{split}\\[-12pt] {z^{\rm T}}{ Q}z = & \left[ \!\!\!{\begin{array}{*{20}{c}} {{z_1}} & {{z_2}} \end{array}}\!\! \right]\left[ \!\!{\begin{array}{*{20}{c}} {{c_1}+hk_1^2} & {h{k_1} - \frac{1}{2}}\\ {h{k_1} - \frac{1}{2}} & h \end{array}} \!\! \right]{\left[ \!\!{\begin{array}{*{20}{c}} {{z_1}} & {{z_2}} \end{array}}\!\! \right]^{\bf T}}= \\ & {\rm{ }} {c_1}z_1^2 - {z_1}{z_2}+hk_1^2z_1^2+2h{k_1}{z_1}{z_2}+hz_2^2 =\\ & {\rm{ }} {c_1}z_1^2 - {z_1}{z_2}+h{\sigma ^2}\text{，} \end{split} $

(18)

其中 ${z^{\rm T}} = \left[ {\begin{array}{*{20}{c}} {{z_1}} & {{z_2}} \end{array}} \right]$。则如果保证Q 为正定矩阵，有

$ {\dot V_2} \leqslant - {z^{\bf T}}{ Q}z - h\beta \left| \sigma \right| \leqslant 0 \text{，} $

(19)

由于

$ \left| { Q} \right| = h\left( {{c_1}+hk_1^2} \right) - {\left( {h{k_1} - \frac{1}{2}} \right)^2} = h\left( {{c_1}+{k_1}} \right) - \frac{1}{4}\text{。} $

(20)

通过取h、c₁ 和k₁ 的值，可使 |Q| ＞ 0，从而保证Q 为正定矩阵，从而保证 ${\dot V_2} \leqslant 0$。

根据 LaSalle 不变性原理，当取 ${\dot V_2} \equiv 0$ 时，$z \equiv 0$，$\sigma \equiv 0$，则t→∞ 时，z→0，σ→0，从而z₁→∞，z₂→∞，则 ${\eta _1} \to {\eta _d}$，${\dot \eta _1} \to {\dot \eta _d}$。

4 仿真研究及结果

现以某船舶^[5]为仿真对象，利用 Matlab 软件来验证基于扩张状态观测器的反演滑模控制器在船舶动力定位系统中的性能，该船舶相关参数如表 1 所示。

船舶模型的质量矩阵和阻尼矩阵分别为：

$ \begin{array}{l} { M} = \left[ {\begin{array}{*{20}{c}} {0.9270} & 0 & 0\\ 0 & {1.7502} & { - 0.1754}\\ 0 & { - 0.1754} & {0.1578} \end{array}} \right] \text{，}\\ { D} = \left[ {\begin{array}{*{20}{c}} {0.0558} & 0 & 0\\ 0 & {0.1183} & { - 0.0402}\\ 0 & { - 0.0151} & {0.0506} \end{array}} \right]\text{。} \end{array} $

仿真实验中，设船舶的起始位置为 $\eta (0) \!\!= $ ${\left[\!\!\!\!\! {\begin{array}{*{20}{c}} {0\;{\rm{m}}}\!\!\! & \!\!\!{0\;{\rm{m}}}\!\!\! & \!\!\!{0^\circ } \end{array}}\!\!\!\!\! \right]^{\rm T}}$，期望位置为 ${\eta _d}\!\! = \!\!{\left[ \!\!\!\!\!{\begin{array}{*{20}{c}} {50\;{\rm{m}}} \!\!\!& \!\!\!{100\;{\rm{m}}} \!\!\!& \!\!\!{20^\circ } \end{array}}\!\!\!\!\! \right]^{\rm T}}$。

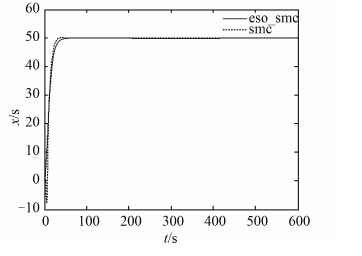
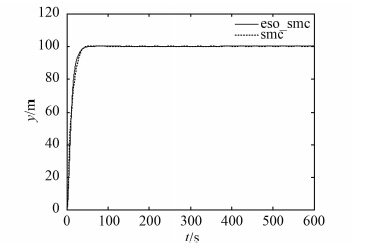
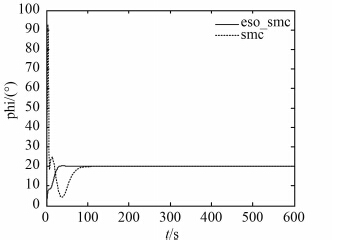
图 2、图 3 和图 4 分别是船舶的纵荡、横荡位置以及首摇角度输出。从图中可发现：在改进滑模控制下的曲线的超调相比于在滑模控制下的曲线的超调小很多，都能够一定误差范围内实现定位功能，避免了系统振荡的情况，增加了系统的稳定性，并且能够较快地到达设定位置，实现定点定位控制。图 5 是船舶的运动轨迹，可以明显地看出基于 ESO 的滑模控制的运动轨迹定位性能远远超过滑模控制下的运动轨迹的定位性能，基于 ESO 的滑模控制的运动轨迹能够快速平稳地到达设定点 [50 m，100 m，20°]，运动效果良好，充分证明了基于扩张观测器的反演滑模控制的有效性和可行性。

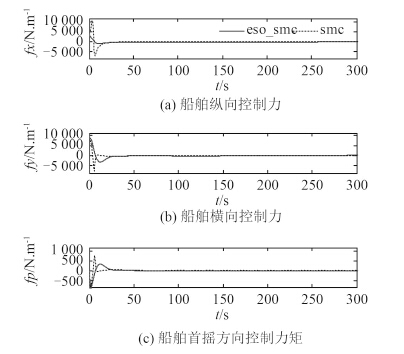
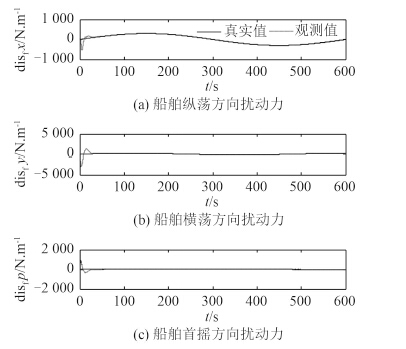
图 6 是船舶的纵荡、横荡和首摇的控制力和力矩。在系统遭受波浪的干扰之后，控制器的输出指令就会变得相当频繁，这也表明了船舶首向的输入指令变化频繁，这样不仅会带来首向的磨损，还会增加耗能，所以需要对每个自由度上的控制力和力矩进行约束，以实现节能的目的。基于 ESO 的反演滑模的控制力和力矩在每个自由度上的力和力矩幅度比较小，可以延长推进器寿命，说明系统稳定性比较好，而滑模控制下的系统输出的控制力和力矩变化幅度比较大，故系统的鲁棒性比较差。图 7 是基于 ESO 的反演滑模控制下扩张观测器观测出的 3 个方向的外界干扰值，可以看出 ESO 在 20 s 左右的时间里基本能准确估计出干扰值。

5 结语

本文针对海洋平台船舶动力定位控制系统，结合反演滑模控制与扩张观测器的优势，提出一种基于扩张观测器的船舶动力定位反演滑模控制方法。由于系统模型不确定性影响和外部干扰组成的复合扰动的存在，利用扩张状态观测器将其相对准确地估计出来，并在控制器中进行补偿。反演滑模控制器不仅具有传统滑模对不确定性的鲁棒特性，还消除了传统滑控制的抖振问题，提高了抗扰性和鲁棒性。最后利用 Matlab 进行了定点控制仿真实验，仿真结果表明，基于扩张观测器的船舶动力定位反演滑模控制方法能够有效提高船舶动力定位运动控制效果，利用 ESO 能够准确估计出系统的复合扰动，而反演滑模控制器能够使系统状态快速收敛，提高了系统的鲁棒性和抗干扰性能。