在理想的工作状态下,舰船推进轴系尾管滑动轴承内孔的中心线和轴系轴颈的中心线应该重合,即两者之间不存在夹角。我国的船舶行业标准[1]CB/Z 338-2005 中则建议尾管后轴承支承点处的轴颈截面转角最好不超过 3.5×10-4 rad(约 0.02°)。如果超过此值则需要对轴承进行斜镗孔处理,使轴承转角符合轴颈转角;如果不超过此值,轴承沿直线基准布置,即忽略轴承和轴线之间的夹角。
但是在实际轴系校中安装时,由于轴段和螺旋桨的重力以及校中工艺的限制等多方面的影响,轴承孔和轴颈中心线之间往往存在一定的不对中夹角误差,其中可分解为铅垂面内的倾角误差和水平面内的摆角误差。
夹角误差的存在使得尾管轴承尤其是尾管后轴承处产生了严重的单边载荷,常常伴随着轴承的边缘磨损[2],严重影响轴承寿命。轴承自身的偏磨还显著影响轴承的承载性能,并对轴系的动态校中性能和舰船振动造成影响[3]。
文献[4-6] 只考虑了轴变形对滑动轴承流体动力特性的影响,但不足以满足船舶轴系校中的需求,尚未研究不对中角度误差角度对轴承工作性能的影响。Piggot[7] 研究结果表明,滑动轴承的轴承孔和轴颈之间的相对夹角达到 0.000 2 rad,轴承的承载性能则会下降 40%。J.Bouyer 和 M.Fillon[8] 的试验表明校中不良引起轴承和轴颈之间的夹角和附加力矩会对滑动轴承性能的显著影响。
文献[9-10] 提出了一种顺应轴系挠度曲线的轴承孔系布置方法,把轴承不对中夹角误差控制在更小的范围内,有利于解决轴承偏磨。本文将基于有限差分法求解 Reynolds 方程[11],分析夹角误差对轴承承载特性的影响规律,为高精度的轴系校中计算提供依据。
1 Reynolds 方程的求解原理船舶轴系在稳定运行时,轴承所受外载荷基本为稳定的静载荷,则可将二维 Reynolds 方程简化为无量纲形式:
| $\frac{\partial }{{\partial \varphi }}\left( {{H^3}\frac{{\partial P}}{{\partial \varphi }}} \right) + {\left( {\frac{d}{L}} \right)^2}\frac{\partial }{{\partial \lambda }}\left( {{H^3}\frac{{\partial P}}{{\partial \lambda }}} \right) = \frac{{\partial H}}{{\partial \varphi }}\text{。}$ | (1) |
式中:
可利用有限差分法求解方程(1),将轴瓦的内表面由偏位角处展开成一平面,然后将该平面进行m × n 的网格划分。沿圆周
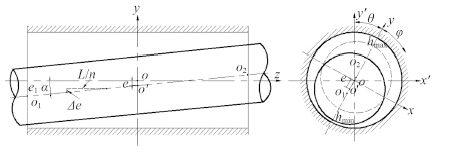
图 1 为只存在倾角误差的滑动轴承模型,O 为轴承孔的中心,O′ 为轴承长度方向中间截面处的轴颈中心,偏心距
|
图 1 存在倾角误差的滑动轴承模型 Fig. 1 A sliding bearing model with inclination angle error |
当轴承的倾角为 0 时,液膜厚度h 的无量纲液膜厚度H 为:
| $H = \frac{h}{c} = \frac{{c + e\cos (\varphi )}}{c} = 1 + \varepsilon \cos \varphi \text{,} $ | (2) |
其中ε 为轴承的偏心率。
当轴颈在轴承孔内发生倾斜时,只要根据倾斜角度计算出沿轴承长度方向每个截面处的偏心距e,根据式(2)便可表示出轴承内部任意处的液膜厚度。
由于把轴承沿长度方向等分成了n 格,根据已知的倾角α,进一步易得每个节点所在横截面的偏心距ej 为:
| $\begin{array}{l} {e_j} \!\!=\!\! e\! \!+\!\! \frac{L}{2} {\rm tan} \alpha \!-\! (j \!-\!\! 1) \!\cdot\! \displaystyle\frac{L}{n}{\rm tan}\alpha \!\!=\!\! e \!\!+\!\! ( \! \frac{1}{2} \!\!-\!\! \displaystyle\frac{{j - 1}}{n}) \!\cdot\! L \!\cdot \!{\rm tan}\alpha \text{,} \end{array}$ | (3) |
其中j = 1,2,3…n + 1。
为求解方便及与 Reynolds 方程的无量纲化相对应,无量纲化液膜厚度H 为:
| $\begin{split} \\[-12pt] H = \displaystyle\frac{h}{c} = & \displaystyle\frac{{c + \left[ {e + (\frac{1}{2} - \frac{{j - 1}}{n}) \cdot L \cdot {\rm tan}\alpha } \right] \cdot \cos \varphi }}{c}=\\ & {\rm{ 1 + }}\left[ {\displaystyle\frac{e}{c} + (\frac{1}{2} - \frac{{j - 1}}{n}) \cdot \frac{L}{c} \cdot {\rm tan}\alpha } \right] \cdot \cos \varphi =\\ & {\rm{ 1 + }}\left[ {\varepsilon + (\displaystyle\frac{1}{2} - \frac{{j - 1}}{n}) \cdot \frac{L}{c} \cdot {\rm tan}\alpha } \right] \cdot \cos \varphi \text{。} \end{split}$ | (4) |
式中:j = 1,2,3…n + 1;
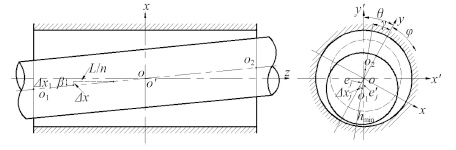
图 2 为同时存在倾角α 及摆角β 误差的滑动轴承模型。在轴承的xoz 平面内,第j 个网格线上的节点所在的截面上的轴颈中心在xoz 平面内的偏摆量为:
|
图 2 存在倾角及摆角误差的滑动轴承模型 Fig. 2 A sliding bearing model with inclination and offset angle error |
| $\Delta {x_j} = \frac{L}{2}{\rm tan}\beta - (j - 1)\frac{L}{n}{\rm tan}\beta = \frac{L}{n} \cdot {\rm tan}\beta \cdot (\frac{n}{2} - j + 1)\text{。}$ | (5) |
由于倾角α,摆角β 的存在,轴颈中心的位置在xoy 平面中与x 轴构成了夹角 γ,其大小可表示为:
| $ \begin{split} \\[-12pt] \tan \gamma = & \displaystyle\frac{{\Delta {x_j}}}{{{e_j}}} = \frac{{\frac{L}{n} \cdot \tan\beta \cdot (\frac{n}{2} - j + 1)}}{{e + (\frac{1}{2} - \frac{{j - 1}}{n}) \cdot L \cdot \tan\alpha }}{\rm{ = }}\\[5pt] & \displaystyle\frac{{\tan\beta \cdot (\frac{n}{2} - j + 1)}}{{ne + (\frac{n}{2} - j + 1) \cdot L \cdot \tan\alpha }}\text{。} \end{split} $ | (6) |
由式(3)和式(6) 可得每个截面的轴颈中心的偏心距为:
| ${e'_j} = {e_j}/\cos \gamma = \frac{{e + (\frac{1}{2} - \frac{{j - 1}}{n}) \cdot L \cdot \tan\alpha }}{{\cos \gamma }}\text{,}$ | (7) |
可得径向润滑轴承任意位置的液膜厚度h 为:
| $\begin{split} \\[-12pt] h = & c + e_j' \cdot \cos \left( {\varphi {\rm{ + }}\gamma } \right) =\\[5pt] & c + \displaystyle\frac{{e + (\frac{1}{2} - \frac{{j - 1}}{n}) \cdot L \cdot \tan\alpha }}{{\cos \gamma }} \cdot \cos \left( {\varphi {\rm{ + }}\gamma } \right)\text{,} \end{split}$ | (8) |
进一步得到包含轴承倾角及摆角误差的无量纲化液膜厚度为:
| $\begin{split} \\[-12pt] & H = \displaystyle\frac{h}{c} = \displaystyle\frac{{c + \frac{{e + \left( {\frac{1}{2} - \frac{{j - 1}}{n}} \right) \cdot L \cdot \tan\alpha }}{{\cos \gamma }} \cdot \cos \left( {\varphi {\rm{ + }}\gamma } \right)}}{c}=\\[5pt] & {\rm{ 1 + }}\left[ {\displaystyle\frac{e}{c} + \left( {\frac{1}{2} - \frac{{j - 1}}{n}} \right) \cdot \frac{L}{c} \cdot \tan\alpha } \right] \cdot \displaystyle\frac{{\cos \left( {\varphi {\rm{ + }}\gamma } \right)}}{{\cos \gamma }}=\\[5pt] & {\rm{ 1 + }}\left[ {\varepsilon + \left( {\displaystyle\frac{1}{2} - \frac{{j - 1}}{n}} \right) \cdot \frac{L}{c} \cdot \tan\alpha } \right] \cdot \displaystyle\frac{{\cos \left( {\varphi {\rm{ + }}\gamma } \right)}}{{\cos \gamma }}\text{。} \end{split}$ | (9) |
其中,j = 1,2,3…n + 1;
对于舰船推进轴系而言,不考虑扰动力的情况下,轴承所受到的外载荷方向通常竖直向下。轴系稳定运行时,轴颈会稳定在轴颈的某个位置,即轴颈有确定的偏位角θ 和偏心率ε,使得液膜水平方向合力为 0,而竖直方向的合力等于轴承负荷。其中液膜水平方向的分力的合力Fx 和竖直方向上分力的合力Fy 可按式(10)求解:
| $ \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {F_x} = \int_{ - 1}^1 {\int_0^{2 } {{P_{ij}}\sin(\theta + \varphi )} }{\rm d} \varphi {\rm d}\lambda \approx \\[5pt] \quad \quad \sum\limits_{i = 1}^{m + 1} {\sum\limits_{j = 1}^{n + 1} {{P_{ij}}\sin(\theta + {\varphi _i})} } \Delta \varphi \Delta \lambda \text{,} \end{array}\\[20pt] \begin{array}{l} {F_y} = \int_{ - 1}^1 {\int_0^{2 } {{P_{ij}}\cos(\theta + \varphi )} } {\rm d}\varphi {\rm d}\lambda \approx \\[5pt] \quad \quad \sum\limits_{i = 1}^{m + 1} {\sum\limits_{j = 1}^{n + 1} {{P_{ij}}\cos(\theta + {\varphi _i})} } \Delta \varphi \Delta \lambda \text{。} \end{array} \end{array}} \right. $ | (10) |
式中:
| $F = \sqrt {{F_x}^2 + {F_y}^2} \approx {F_y}\text{,}$ | (11) |
求解船舶轴系稳定运行时的承载力时根据收敛条件
| $\left\{ \begin{array}{l} f(\varepsilon ) = \left| {\frac{{W - {F_y}}}{W}} \right| < ERR\text{,}\\ g(\theta ) = \left| {\frac{{{F_x}}}{{{F_y}}}} \right| < ERR\text{。} \end{array} \right.$ | (12) |
其中:W 为轴承所受外载荷;ERR 可取 10-4。由式(15)便可迭代求出合适的偏心率ε 和偏位角θ。
3.2 轴承处的附加力矩对于舰船推进轴系而言,尾管轴承内孔与轴颈之间的不对中倾角和摆角误差,会引起轴承内部液膜厚度分布不均,油膜压力不对称,此时即使液膜压力的合力为 0,在轴承部位也会引起附加的力矩。
其中把图 1 和图 2 所示平面内的逆时针方向的力矩定义为正。根据轴承液膜压力的分布特点,液膜压力对x 轴,y 轴产生的附加无量纲力矩可分别表示为:
| $ \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} \!\!\!\!\!\!\!\!\!\!{M_x} = {\rm{ - }}\int_{ - 1}^1 {\int_0^{2 } {{P_{ij}}\cos (\theta + \varphi )} } \lambda {\rm d}\varphi {\rm d}\lambda \approx \\[5pt] \!\!\!\!{\rm{ - }}\sum\limits_{i = 1}^{m + 1} {\sum\limits_{j = 1}^{n + 1} {{P_{ij}}\cos(\theta \!+\! {\varphi _i})\left[ { \!-\! 1 \!+\! \Delta \lambda \cdot (j \!-\! 1)} \right]} } \Delta \varphi \Delta \lambda \text{,} \end{array}\\[15pt] \begin{array}{l} \!\!\!\!\!\!\!\!\!\!{M_y} = {\rm{ - }}\int_{ - 1}^1 {\int_0^{2 } {{P_{ij}}{\rm sin}(\theta + \varphi )\lambda } } {\rm d}\varphi {\rm d}\lambda \approx \\[5pt] \!\!\!\!{\rm{ - }}\sum\limits_{i = 1}^{m + 1} {\sum\limits_{j = 1}^{n + 1} {{P_{ij}}\sin(\theta \!+\! {\varphi _i})} } \left[ { - 1 \!+\! \Delta \lambda \cdot (j \!-\! 1)} \right]\Delta \varphi \Delta \lambda \text{。} \end{array} \end{array}} \right. $ | (13) |
则作用在轴承处的无量纲力矩矢量M 及其φM 方向角为:
| $\left\{ \begin{array}{l} M = \sqrt {{M_x}^2 + {M_y}^2} \text{,}\\ {\varphi _M} = {\rm{arctan}}\frac{{{M_x}}}{{{M_y}}}\text{。} \end{array} \right.$ | (14) |
由摩擦学原理[12] 可知,径向滑动轴承沿运动方向的总的摩擦阻力为:
| $F = \int_{ - L/2}^{L/2} {\int_0^x {{\tau _x}{|_{y = h}}{\rm d}A} }\text{,} $ | (15) |
由于在船舶推进轴系的滑动轴承中,液膜分成了油膜承载区和液膜破裂区。设液膜承载区的边界为x1,则由式(15)可得径向滑动轴承液膜承载区沿运动方向的总的摩擦阻力为:
| ${F_1} \!\!=\!\! \int_{ - L/2}^{L/2} {\int_0^{{x_1}} {{\tau _x}{\rm d}x{\rm d}z} } \!\!=\!\! \int_{ - L/2}^{L/2} {\int_0^{{x_1}} {\left( {\frac{h}{2}\frac{{\partial p}}{{\partial x}} \!\!+\!\! \frac{{\eta U}}{h}} \right){\rm d}x{\rm d}z} }\text{,} $ | (16) |
根据上节所述的无量纲形式,将式(16)进行无量纲化,有
| $\begin{split} \\[-12pt] & {F_1} = \displaystyle\int_{ - L/2}^{L/2} {\int_0^{{x_1}} {\left( {\frac{h}{2}\frac{{\partial p}}{{\partial x}} + \frac{{\eta U}}{h}} \right){\rm d}x{\rm d}z} } =\frac{{3\eta UrL}}{{2c}}\\ & \ \displaystyle\int_{ - 1}^1 {\int_0^{{\varphi _1}} {\left( {H\displaystyle\frac{{\partial p}}{{\partial \varphi }}} \right){\rm{d}}\varphi {\rm{d}}\lambda } } + \displaystyle\frac{{\eta UrL}}{{2c}}\int_{ - 1}^1 {\int_0^{{\varphi _1}} {\displaystyle\frac{1}{H}{\rm{d}}\varphi {\rm{d}}\lambda } } = \\ & \ {\rm{ }}\displaystyle\frac{{\eta UrL}}{{2c}}\int_{ - 1}^1 {\int_0^{{\varphi _1}} {\left( {3H\frac{{\partial p}}{{\partial \varphi }} + \frac{1}{H}} \right){\rm d}\varphi {\rm d}\lambda } } \text{,} \end{split}$ | (17) |
可得油膜承载区内的无量纲摩擦阻力为:
| $\overline {{F_1}} = \frac{{{F_1}}}{{\frac{{\eta UrL}}{{2c}}}}{\rm{ = }}\int_{ - 1}^1 {\int_0^{{\varphi _1}} {\left( {3H\frac{{\partial p}}{{\partial \varphi }} + \frac{1}{H}} \right)d\varphi d\lambda } }\text{。} $ | (18) |
其中
根据 Reynolds 的求解原理,式(18)可用下式的矩形积分法求解无量纲摩擦力为:
| $ \begin{split} \\[-12pt] \overline {{F_1}} {\rm{ = }}\int_{ - 1}^1 {\int_0^{{\varphi _1}} {\left( {3H \displaystyle\frac{{\partial p}}{{\partial \varphi }} + \frac{1}{H}} \right){\rm d}\varphi {\rm d}\lambda } } \approx \\ \quad \quad \sum\limits_{i = 1}^{{m_\varphi }} {\sum\limits_{j = 1}^{n + 1} {\left( {3{H_i}_j \displaystyle\frac{{{p_{i + 1,j}} - {p_i}_j}}{{\Delta \varphi }} + \frac{1}{{{H_{ij}}}}} \right)} } \Delta \varphi \Delta \lambda \text{。} \end{split} $ | (19) |
其中
此外,在轴承的非承载区,液膜破裂形成液膜破裂区。此时的液膜流量总宽度应该随着间隙厚度的增加而减小,根据截面流量守恒理论,采用当量宽度
液破裂区的摩擦力阻力为:
| ${F_2} = \int_{ - L/2}^{L/2} {\int_{{x_1}}^{2 r} {\frac{{\eta U}}{h} \cdot \frac{{{h_1}}}{h}{\rm d}x{\rm d}z} } \text{,}$ | (20) |
根据上节所述的无量纲形式,将式(20)进行无量纲化,有
| $\begin{split} \\[-12pt] {F_2} = & \int_{ - L/2}^{L/2} {\int_{{x_1}}^{2 r} {\displaystyle\frac{{\eta U}}{h} \cdot \frac{{{h_1}}}{h}{\rm d}x{\rm d}z} } =\\ & {\rm{ }}\int_{ - 1}^1 {\int_{{\varphi _1}}^{2 } {\displaystyle\frac{{\eta U}}{{Hc}} \cdot \frac{{{H_1}c}}{{Hc}} \cdot \frac{L}{2} \cdot r{\rm d}\varphi {\rm d}\lambda } } =\\ & {\rm{ }}\displaystyle\frac{{\eta ULr}}{{2c}}\int_{ - 1}^1 {\int_{{\varphi _1}}^{2 } {\frac{{{H_1}}}{{{H^2}}}{\rm d}\varphi {\rm d}\lambda } } \text{。} \end{split}$ | (21) |
可得油膜破裂区内的无量纲摩擦阻力为:
| $\overline {{F_2}} {\rm{ = }}\frac{{{F_2}}}{{\displaystyle\frac{{\eta ULr}}{{2c}}}} = \int_{ - 1}^1 {\int_{{\varphi _1}}^{2 } {\frac{{{H_1}}}{{{H^2}}}{\rm d}\varphi {\rm d}\lambda } }\text{,} $ | (22) |
其中
| $\overline {{F_2}} {\rm{ = }}\int_{ - 1}^1 {\int_{{\varphi _1}}^{2 } {\frac{{{H_1}}}{{{H^2}}}{\rm d}\varphi {\rm d}\lambda } } {\rm{ = }}\sum\limits_{i = {m_\varphi }}^{m + 1} {\sum\limits_{j = 1}^{n + 1} {\frac{{{H_{1(i,j)}}}}{{H_{i,j}^{^2}}}} } \Delta \varphi \Delta \lambda \text{,}$ | (23) |
其中
由式(19)和式(23)可得整个轴承液膜对轴颈的无量纲摩擦力为:
| $\overline F = \overline {{F_1}} + \overline {{F_2}} \text{。}$ |
在船舶轴系校中时,尾管轴承因其特殊的支承位置和受力情况常存在较大的不对中倾角及摆角误差,本文以某船舶推进轴系的尾管轴承为例进行分析,其具体参数如表 1 所示。分别研究尾管轴承的安装倾角和摆角误差对轴承的液膜压力分布、轴承承载能力、附加力矩及轴颈运转摩擦力的影响规律。
|
|
表 1 轴颈及轴承参数表 Tab.1 The list of journal and bearing parameter |
分析轴承的润滑特性时,取轴承中间截面的偏心率为 0.8,得到不同倾角α 及摆角β 下的无量纲液膜压力分布,如图 3 所示。

|
图 3 夹角误差影响下的无量纲液膜压力的等值线图 Fig. 3 The contour map of the dimensionless film pressure under the influence of angle error |
由图 3(a) 和图3(b)可知,轴承轴颈的倾斜角度对轴承的液膜压力分布有着显著影响,最大液膜压力的位置随着轴颈倾斜角度的增加不断的向轴承的某一特定端部移动,形成偏载。这表明当轴系校中不合理或者轴系校中不良时,轴系支承的作用点不能简单的简化在轴承中间位置,而要根据轴颈的倾斜角度进行适当的修正。此外,无量纲液膜压力的峰值会随着轴颈倾斜角度的增大而升高,倾斜的角度越大,液膜压力峰值升高的就越明显,进而对轴系校中的影响就越大。
轴颈倾斜角度在小于国标规定的 3.5 × 10-4 rad 甚至 0.01° 以下时,就出现了明显的载荷分布不均现象,单边最大无量纲液膜压力由 1.97 增加到 2.91,增加了 47.7%。这将导致轴承产生严重的边缘效应,如图 3(b)所示,一端边缘就成了主要的受力点,轻微的扰动就有可能导致轴颈和轴承的接触摩擦,甚至导致润滑失效,液膜破损,引起轴承偏磨。
由图 3(c)可知,最大液膜压力的位置随着轴颈摆角的增加会逐步的向轴承的两端移动,并随着摆角的增加而愈加明显,最终在轴承两端部的边缘处形成 2 个峰值,沿轴承长度方向形成不均匀的载荷分布,从而引起两端部的边缘载荷,导致轴颈和轴承的接触摩擦,甚至导致润滑失效。
由图 3(a)和图 3(c)中可看出,轴承的摆角误差还会引起沿轴向方向轴承内部承载区域倾斜,这是由于轴向不同圆周截面的最小液膜厚度的位置由于摆角的存在而变化引起的。
此外,相同的角度误差下,倾角误差对轴承无量纲液膜压力的影响远大于摆角误差,因此轴承的承载特性主要表现出倾角误差的特性。轴颈的摆角使得原处的最小液膜厚度变大,一定程度上减轻了因倾角引起的油膜不均匀程度,从而减缓了轴颈倾斜导致的边缘效应,但缓解作用十分有限。
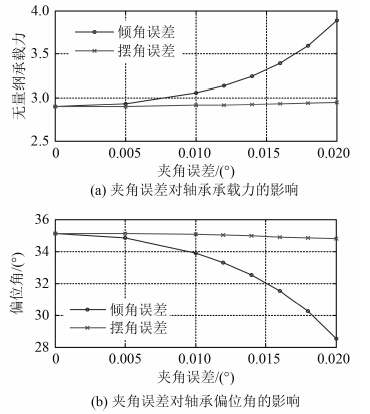
图 4 为夹角误差对轴承承载性能的影响。通过分析可知,轴颈倾角误差使得最小液膜厚度变小,引起最大液膜压力显著的增加,因此随着倾角误差的增大,总体表现的轴承承载力就越大,偏位角就越小。
|
图 4 夹角误差对轴承承载性能的影响 Fig. 4 Influence of angle error on bearing bearing performance |
但是,倾角误差越大,其引起的沿轴承长度方向的承载力分布就越不均匀,边缘效应就越加严重,影响轴承的使用寿命。相比之下,由于摆角误差存在于水平面内,且液膜压力变化具有对称性,因此对铅垂面内的轴承承载能力影响不大,所以要更加严格的控制轴承安装的倾角误差。
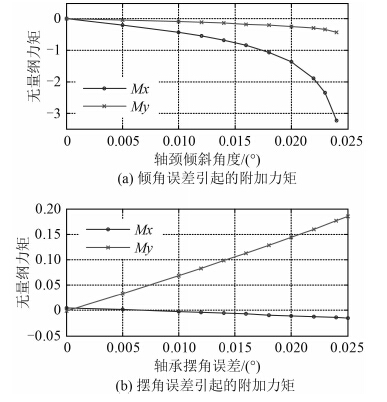
图 5 分别为不同的倾角、摆角误差在轴承处引起的附加力矩。倾角误差对铅垂面的力矩Mx 有显著影响,随着倾角误差的增大,力矩Mx 就会显著增加。而对水平面内的力矩My 的影响较小。相反随着倾角误差的增大,力矩My 就越大且基本呈线性增长,而对水平面内的力矩Mx 影响较小。总体来看,无论是倾角误差还是摆角误差,轴承安装夹角误差的存在,即使在国标规定的 3.5 × 10-4 rad(约 0.02°)以内,也在轴承处产生了极其显著的附加力矩,这将继续影响轴系的校中效果,引起轴颈平衡位置的变化,轴心的涡动,甚至振动失稳。
|
图 5 不对中夹角误差引起的附加力矩 Fig. 5 The additional torque caused by misalignment angle error |
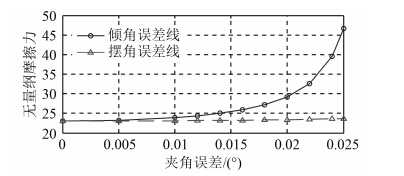
轴承不对中夹角误差对无量纲摩擦阻力的影响如图 6所示。倾角误差和摆角误差的增大都会引起轴颈摩擦力的增大。其中,摆角误差的存在对轴颈运转摩擦力的影响并不大,基本可以忽略;但倾角误差的存在会对轴颈摩擦力产生显著影响。对此对轴承而言,即使把轴承的安装倾角误差控制在国标值 3.5 × 10-4 rad 以下,轴颈受到的无量纲摩擦力就由 23.01 增加到 29.13,增加了 26.60%。随着倾角的增加,轴颈摩擦力增加趋势更加明显。
|
图 6 轴承不对中夹角误差对轴颈无量纲摩擦阻力的影响 Fig. 6 Effect of misalignment angle error on dimensionless frictional resistance of bearing |
综上所述,在船舶推进轴系的设计及校中安装中,由于螺旋桨及轴段的重力和校中工艺等影响引起的轴承内孔和轴颈之间的倾角和摆角误差,即使控制在标准规定的 3.5 × 10-4 rad 以下,依然会对轴承的承载性能产生显著影响。随着夹角误差的增大,最小液膜厚度减小,最大液膜压力显著增大且向轴承一端或者两端移动,造成轴承承载不均,引起偏磨。此外,轴承安装误差的存在,还会引起轴承内部的附加力矩,运转摩擦阻力大幅度增加,影响轴承的稳定工作及轴系校中效果。
同时建议采用顺应轴系曲线轴线安装轴承的工艺方法,避免或者减小轴承不对中的倾角误差,同时提高轴承的安装精度,消减摆角误差,保证轴承良好的润滑效果和承载性能。
| [1] |
CB/Z 338-2005, 船舶推进轴系校中[S].
CB/Z 338-2005, Ship propulsion shafting alignment[S]. |
| [2] | 周继良, 邹鸿均. 船舶轴系校中原理及其应用[M]. . |
| [3] |
朱理, 庞福振, 康逢辉. 螺旋桨激励力下的舰船振动特性分析[J]. 中国造船, 2011, 52 (2): 8–15.
ZHU Li, PANG Fu-zhen, KANG Feng-hui. Vibration characteristic of a warship subjected to propeller excitation[J]. shipbuilding of china, 2011, 52 (2): 8–15. |
| [4] |
孙军, 桂长林, 李震, 等. 计入轴变形导致轴颈倾斜的径向滑动轴承流体动力润滑分析[J]. 机械科学与技术, 2005, 24 (2): 204–207.
SUN Jun, GUI Chang-lin, LI Zhen, et al. Hydrodynamic lubrication analysis of misaligned journal bearing caused by shaft deformation[J]. Mechanical Science and Technology, 2005, 24 (2): 204–207. |
| [5] | SUN Jun, GUI Chang-lin. Hydrodynamic lubrication analysis of journal bearing considering misalignment caused by shaft deformation[J]. Tribology International, 2004, 37 (10): 841–848. DOI: 10.1016/j.triboint.2004.05.007 |
| [6] |
贾小俊, 范世东. 考虑轴颈倾斜的径向滑动轴承动态特性研究[J]. 船海工程, 2008, 37 (5): 54–57.
JIA Xiao-jun, FAN Shi-dong. Dynamic lubrication characteristics analysis of journal bearing considering misalignment[J]. Ship & Ocean Engineering, 2008, 37 (5): 54–57. |
| [7] | PIGGOTT R J S. Bearing troubles traceable to design can be avoided by engineering study[J]. Bearings and lubrication, 1942, 64 : 259–269. |
| [8] | BOUYER J, FILLON M. An experimental analysis of misalignment effects on hydrodynamic plain journal bearing performances[J]. Journal of Tribology, 2002, 124 : 313–319. DOI: 10.1115/1.1402180 |
| [9] |
张新宝, 吴飞, 董广坤, 等. 一种顺应轴系挠度曲线的轴承孔系布置方法[J]. 船舶标准化工程师, 2015 (1): 52–55.
ZHANG Xin-bao, WU Fei, Dong Guang-kun, et al. Layout method of arrangement of bearing holes conforming to deflection curve[J]. Ship Standardization Engineer, 2015 (1): 52–55. |
| [10] |
张新宝, 董广坤. 计入推力的轴系合理校中的轴承负荷比优化及轴线设计[J]. 机械科学与技术, 2015, 34 (10): 1517–1520.
ZHANG Xin-bao, DONG Guang-kun. Optimization design of load ratio between bearings in rational alignment of propulsion shaft considering propulsion force[J]. Mechanical science and technology, 2015, 34 (10): 1517–1520. |
| [11] |
敏政, 王乐, 魏志国, 丁大力. 基于MATLAB技术的滑动轴承油膜压力分布的模拟[J]. 润滑与密封, 2008, 33 (8): 51–57.
MIN Zheng, WANG Le, WEI Zhi-guo, et al. Simulation on pressure distribution of sliding bearing based on Matlab technology[J]. Lubrication Engineering, 2008, 33 (8): 51–57. |
| [12] | 邱明, 陈龙, 李迎春. 轴承摩擦学原理及应用[M]. 北京: 国防工业出版社, 2012. |
 2017, Vol. 39
2017, Vol. 39
