复杂轴承支撑结构的传递路径相对复杂,整个支撑结构一般包括油膜减振器、弹性鼠笼结构、法兰盘等,这些结构的存在使得轴承支撑结构中存在较多的螺栓联接结合面,影响系统的振动特性。这种复杂轴承支撑结构广泛使用于船用燃气轮机等设备,对结构减振起到了一定的作用。但与此同时,由于复杂结构的存在,在对轴承进行故障诊断的过程中,传感器的位置往往只能布置在机匣外侧,振动信号在传递过程中产生的衰减、反射使得故障诊断的难度进一步提高,所以,研究复杂轴承支撑结构的振动传递特性就显得尤为重要。陈果[1]为了研究航空发动机的整机振动情况,建立的新型转子-滚动轴承-机匣耦合动力学模型,考虑了弹性支承和挤压油膜的作用、考虑了转子于机匣间的碰摩故障,有效的研究了系统的动力学特性。然而,接触问题并没有作为一个重要的环节加以研究,实际上,支承结构中存在众多通过螺栓连接的结合面,这些结合面对整个系统的振动有着重要的影响。据统计,机床中出现的振动问题有 60% 以上源自结合面[2],所以在模型建立的过程中突出结合面的的影响可以使得仿真研究的结构更具实际参考价值。
本文以实验室高速复杂结构设备滚动轴承故障模拟平台的滚动轴承支承结构为研究对象,建立轴承支撑结构的有限元计算模型,重点分析结构中的法兰连接结构对结构传递特性的影响,研究螺栓预紧力的变化对系统振动特性的影响;计算系统的模态和传递函数,模拟结构受到轴承故障信号的冲击,研究响应的特点,综合以上方法分析滚动轴承支撑结构的振动传递特性。
1 有限元模型的建立本文研究的滚动轴承支承结构主要包括弹性鼠笼支撑、油膜减振器、法兰盘、机匣等零部件,如图 1 所示。支撑结构中,弹性鼠笼结构通过右侧的螺栓连接在内法兰盘上,左端为自由端,中间部分为鼠笼条。自由端的环圈内安放有实验用的滚动轴承,油膜减振器外支承与弹性鼠笼结构间存在一定的间隙,作为油腔来使用。

|
图 1 复杂轴承支撑结构 Fig. 1 Complex bearing support structure |
在有限元建模的过程中,需要利用软件将实际的物体构造出来,为了更好地反映轴承支撑结构的实际情况,本章利用软件 UG NX8.5,采用 1∶1 建模的方法分别对支撑结构中的弹性鼠笼支撑、油膜减振器外支撑、内法兰和外法兰进行建模,之后进行装配,从而形成轴承支撑结构的模型,将建立好的模型导入 Ansny Workbench 中进行网格划分和有限元计算。
在有限元分析之前,需要对模型进行一定的处理,分析结构可以发现,轴承支撑结构中,油膜减振器外支撑和内法兰、内法兰和外法兰间都是通过 4 个螺栓结构连接在一起,所以模型处理的重点就是这 2 组螺栓连接结构及其形成的接触面,将支撑结构分为整体模型和螺栓结构模型 2 种进行处理。建立整体结构模型时,忽略螺栓结构对结构的影响,将内、外法兰、油膜减震器外支撑和螺栓看成一个整体,将这几个结构之间的所有接触都设置为绑定,同时由于在实际条件下,轴承支承结构是与底座固定在一起,所以在模型建立时将结构的底部设置为固定约束,限制其 6 个自由度方向的运动,保证与实际状况相符合。
当考虑螺栓结构的作用时,将油膜减振器外支撑和内法兰、内法兰和外法兰之间的接触设成摩擦接触,摩擦系数为 0.15[3],其余部分仍然设置为绑定,同时在螺栓上施一定的预紧力,结构的底部同样设置为固定约束。
2 模态计算分析在实际的结构中,对螺栓的拧紧是通过扭矩扳手施加不同的力矩来实现的,但在有限元分析时,需要将对螺母施加的扭矩改为对螺栓实际预紧力来实现。螺栓所受预紧力的大小与所受扭矩的大小关系为[4]:
| $ T = KFd \text{。} $ | (1) |
式中:T 为拧紧螺母所需的力矩;F 为螺栓所受的预紧力;K 为扭矩系数,K 的值可近似取为 0.2;d 为螺纹的大径。利用式(1),可将结构中螺母实际所受力矩转化成螺栓所受的预紧力。
在有限元模型中,分析螺栓分别受到大小为 10 Nm,20 Nm,30 Nm 的拧紧力矩时的各阶模态频率值,利用式(1)将拧紧力矩转换成螺栓预紧力进行添加,同时保证 8 个螺栓的预紧力大小相同,前 6 阶模态频率值如表 1 所示,整体结构的前 6 阶振型如图 2 所示,考虑螺栓结构时的前 6 阶振型如图 3 所示。
|
|
表 1 轴承支撑结构前 6 阶模态频率值 Tab.1 The first six modals of the bearing support structure |

|
图 2 整体结构的前 6 阶振型 Fig. 2 The first six vibration modes of the whole structure |

|
图 3 螺栓连接结构的前 6 阶振型 Fig. 3 The first six vibration modes of bolt connection structure |
分析表 1 中的数据,比较整体结构和螺栓连接结构的各阶固有频率可以看出,相比于整体结构,当考虑螺栓连接时,整个系统的各阶固有频率都有一定的减小,在阶数较低时,固有频率的差距较小,阶数较高时,两者的差异变得十分明显,所以,为了研究的简便而将螺栓连接结构做刚性连接处理会对后续的研究结果产生较大的影响,同时,螺栓连接结构对振型的影响也能够从图 2 和图 3 的对比中体现出来。
当螺栓预紧力增大时,轴承支撑结构的各阶模态频率值都有所提高,这种现象的产生与理论分析一致,当螺栓预紧力增大时,接触面的表面压力增大,导致接触刚度增大[5-6],提高了系统的整体刚度,从而会使得结构的各阶固有频率提高。
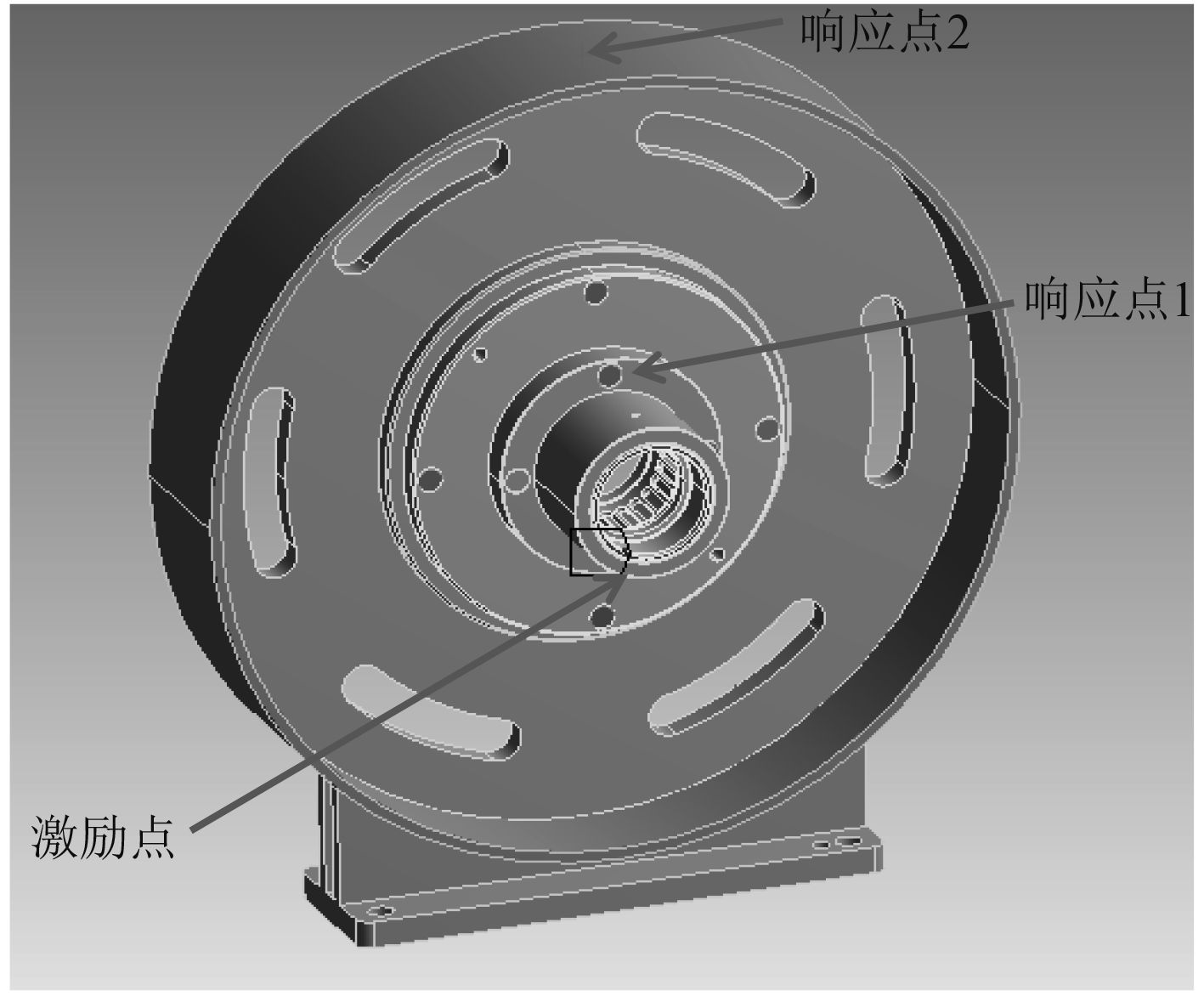
3 复杂轴承支撑结构传递特性分析如图 4 所示,选取弹性鼠笼结构上一点为激励点,分别选取内法兰和机匣上一点作为响应点,在有限元软件中对结构进行谐响应分析,当激励为一个全频的单位力时,响应点的频率响应即可作为结构的传递函数,此时仍然计算整体结构和螺栓受 20 Nm 的拧紧力矩时测点 1 和测点 2 的幅频特性,结果如图 5 和图 6 所示。
|
图 4 结构中激励点、响应点分布图 Fig. 4 The distribution of excitation point and response point in the structure |
|
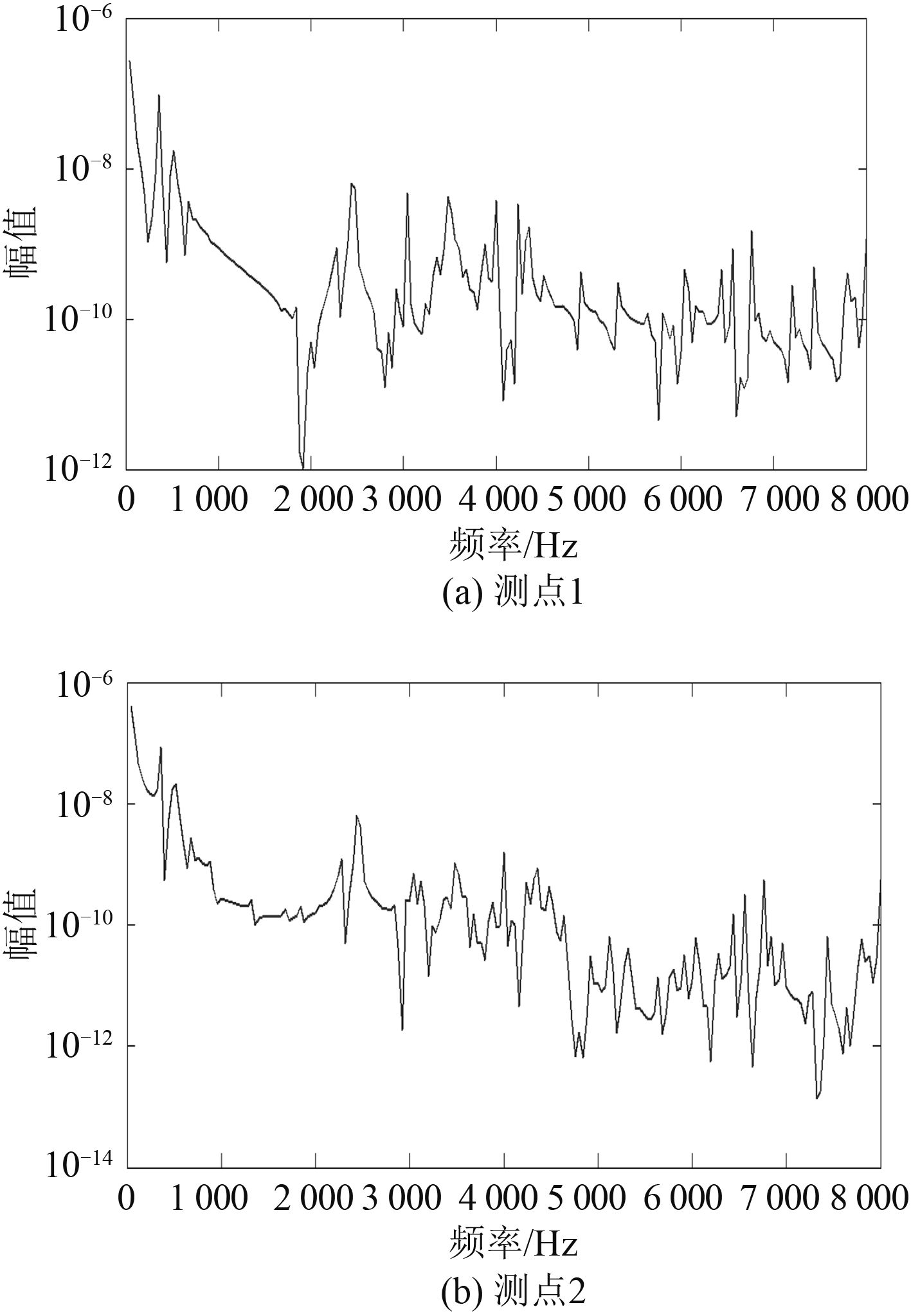
图 5 整体结构的幅频特性曲线 Fig. 5 The amplitude frequency characteristic curve of the whole structure |
|
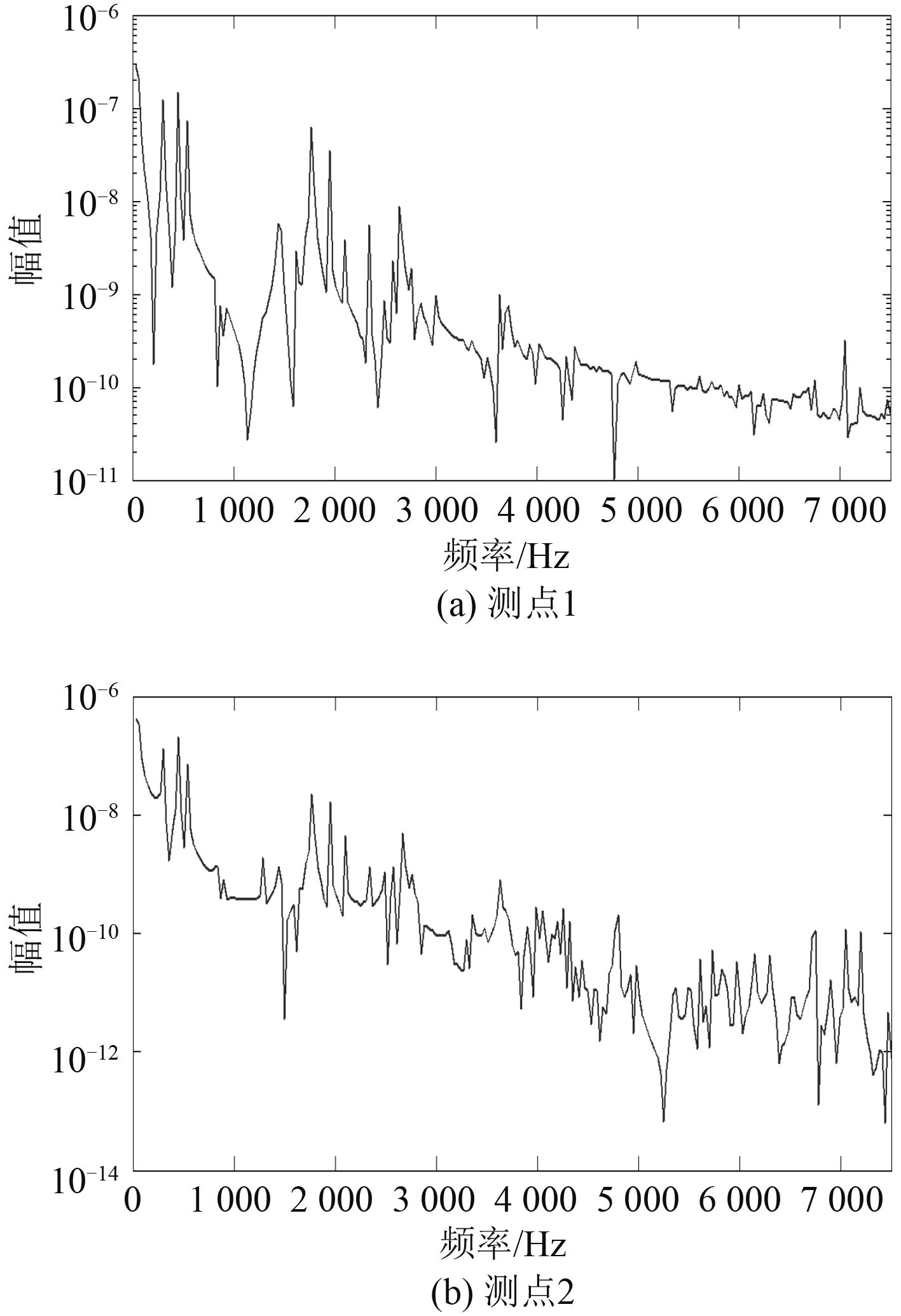
图 6 拧紧力矩为 20 Nm 时的幅频特性曲线 Fig. 6 The amplitude frequency characteristic curve when tightening torque is 20 Nm |
分析图 5 中的曲线可发现,对于整体结构来说,测点 1 和测点 2 处的幅频特性曲线的变化趋势基本类似,由于结构本身的阻尼较小,测点 1 到测点 2 间信号的衰减幅度也较小,同时,信号的传递效果随着频率增大的改变并不明显。当考虑螺栓连接结构时,分析测点 1 和测点 2 的幅频特性曲线可知,随着信号频率的增大,信号传递效果明显变差,尤其是测点 2 处的频响曲线,衰减非常明显。随着频率的提高,相比于测点 1、测点 2 处信号的衰减趋势要更加明显。比较整体结构和螺栓结构各测点的幅频特性曲线,信号从测点 1 传到测点 2 的过程中存在不同程度的衰减,同时,从图 6 中可看出,螺栓连接结构的存在,使得信号在高频处的衰减作用要更加明显,而且随着频率的不断提高,螺栓结构对信号的衰减作用越来越明显,这对高频信号的传递相当不利。
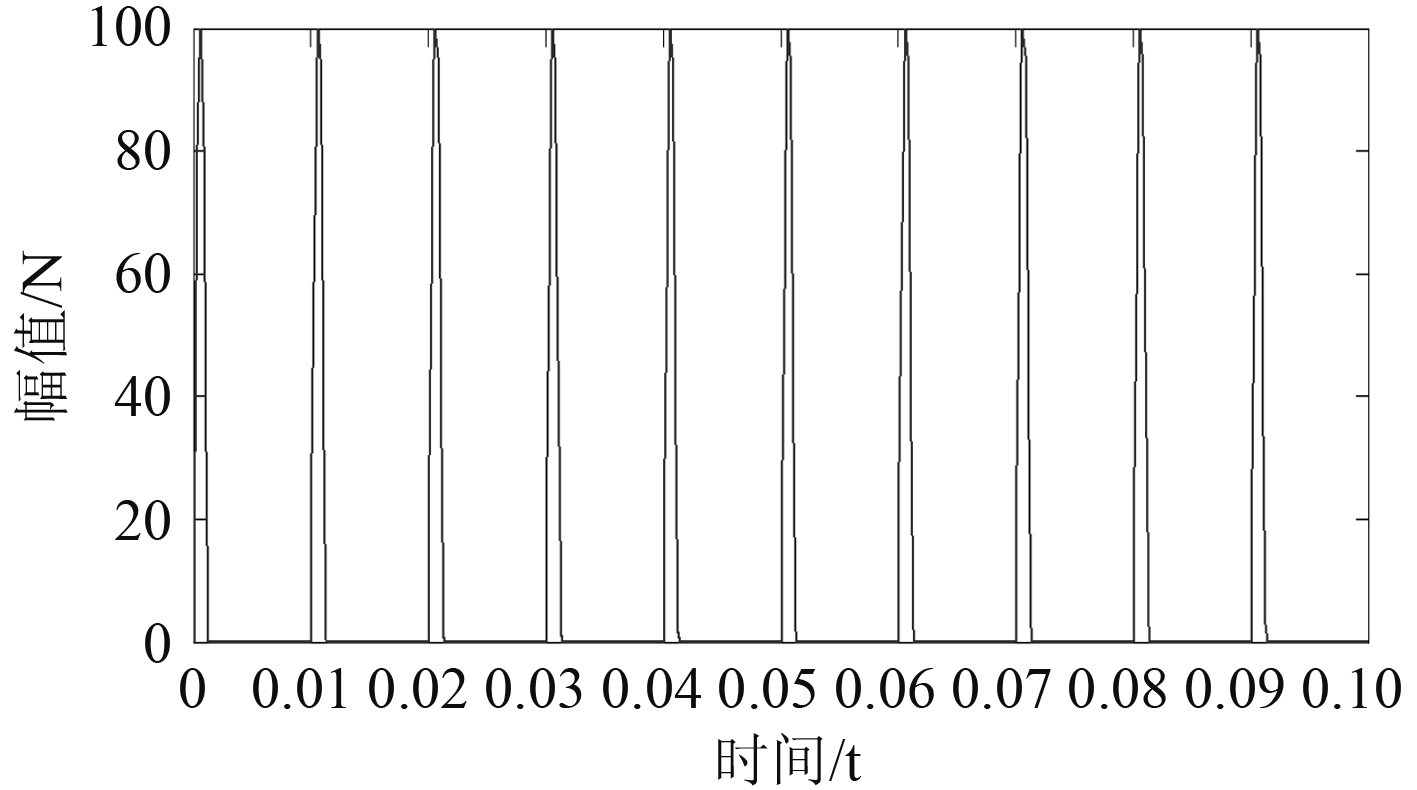
为了进一步研究螺栓连接结构对信号传递的影响,下面将模拟轴承故障信号,对弹性鼠笼结构进行激励,研究测点 1 和测点 2 处的响应信号。激励信号如图 7 所示,脉冲的频率为 100 Hz,由于三角波信号的宽度很小,为 0.001 s 左右,所以可将它作为理想的脉冲信号来使用。
|
图 7 轴承故障模型信号 Fig. 7 Bearing fault signal |
分别取测点 1 和测点 2 处轴向和径向的响应信号,分析螺栓结构对信号传递的影响,结果如图 8~图 11所示。
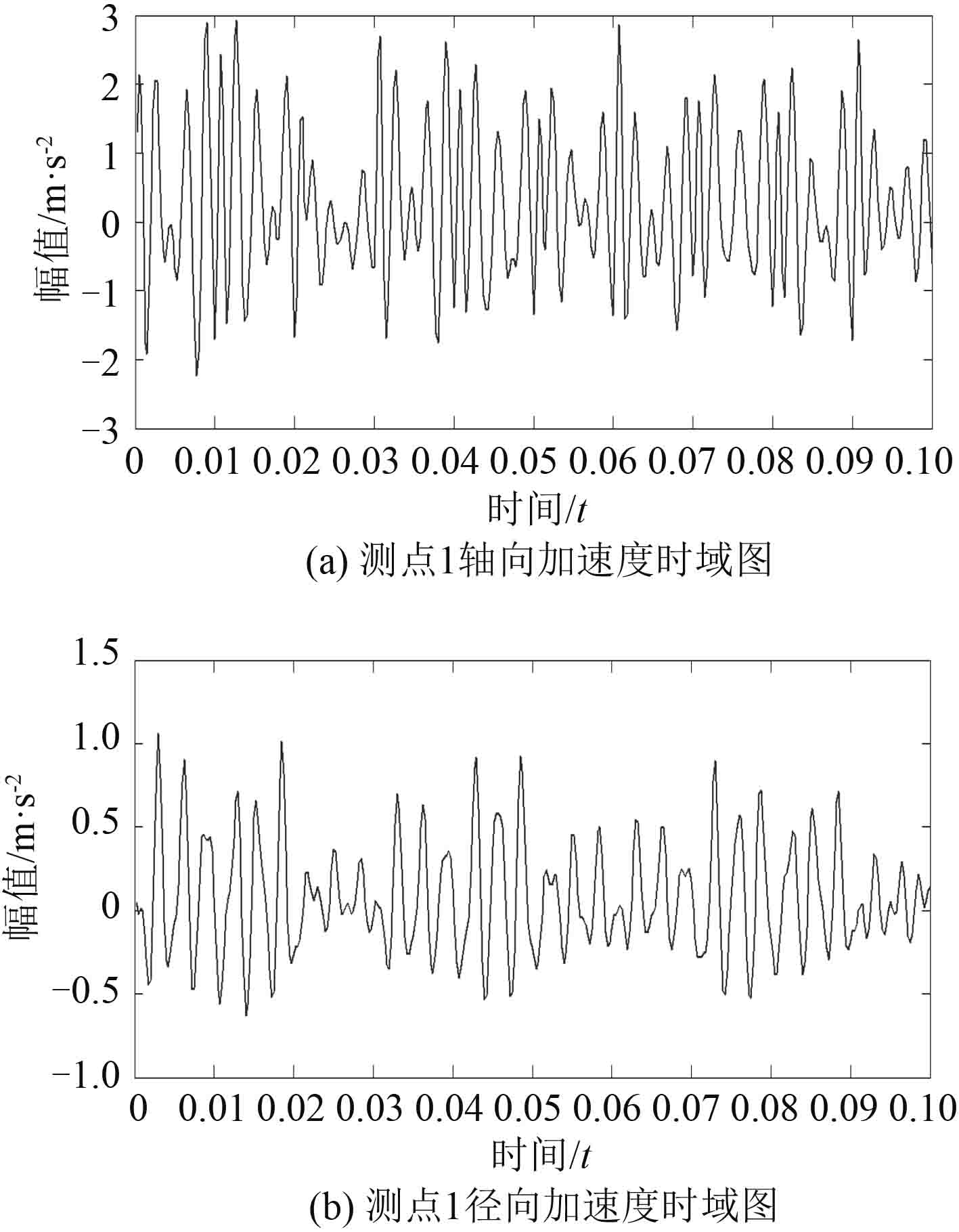
|
图 8 整体结构测点 1 的加速度时域图 Fig. 8 The acceleration time domain of the whole structure in measuring point 1 |
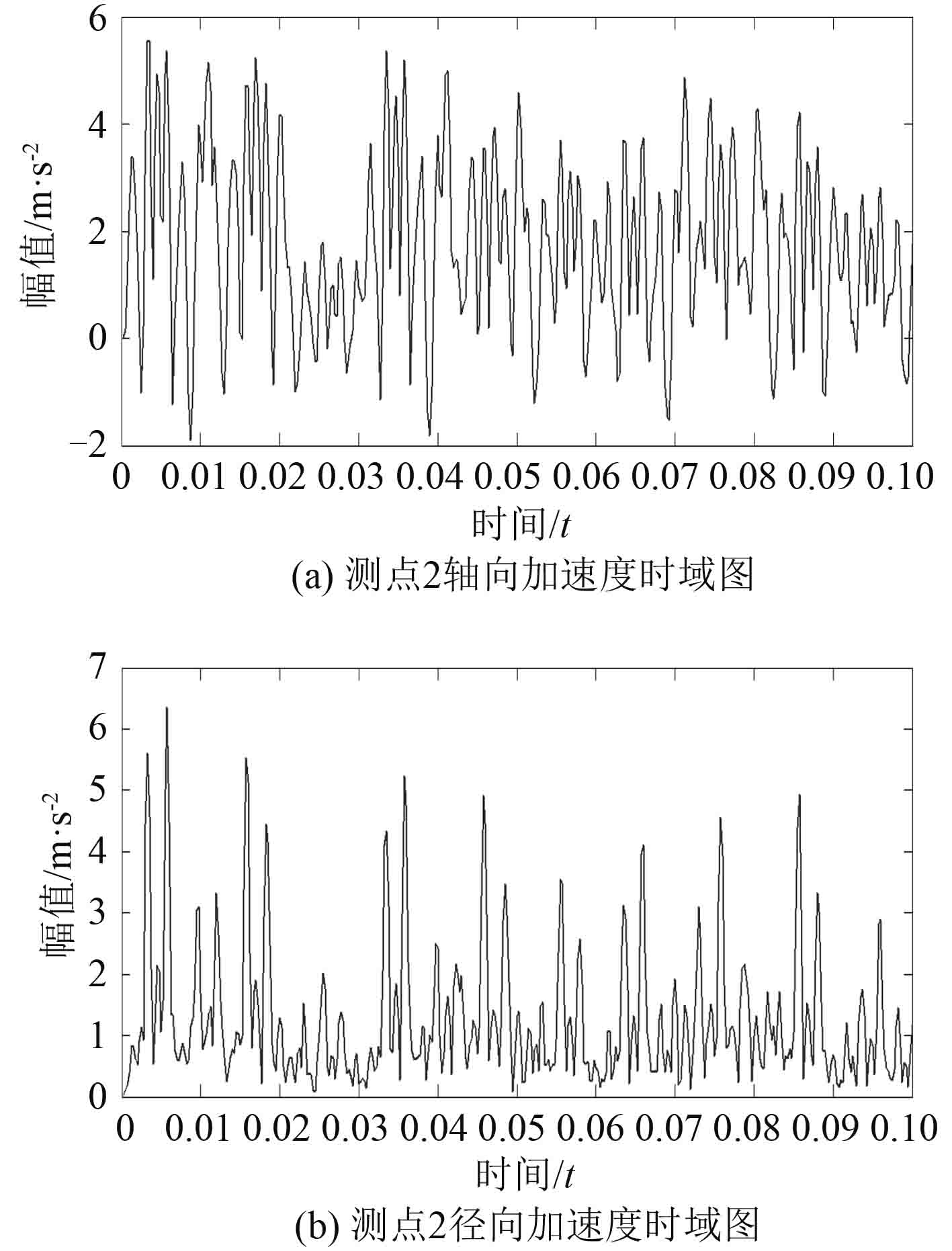
|
图 9 整体结构测点 2 的加速度时域图 Fig. 9 The acceleration time domain of the whole structure in measuring point 2 |
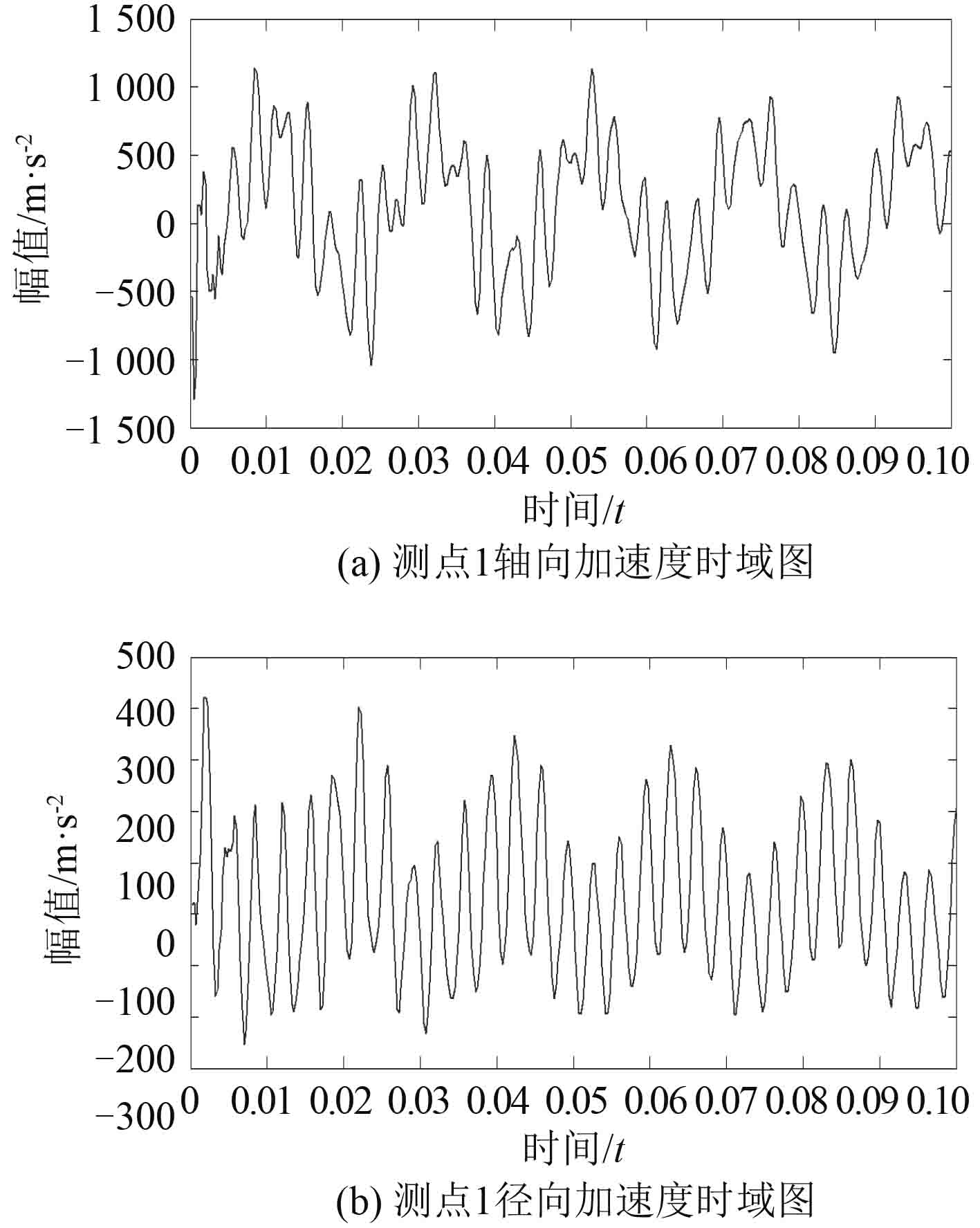
|
图 10 考虑螺栓连接的支承结构测点 1 的加速度时域图 Fig. 10 The acceleration time domain of the structure in measuring point 1 when bolt connection is considered |
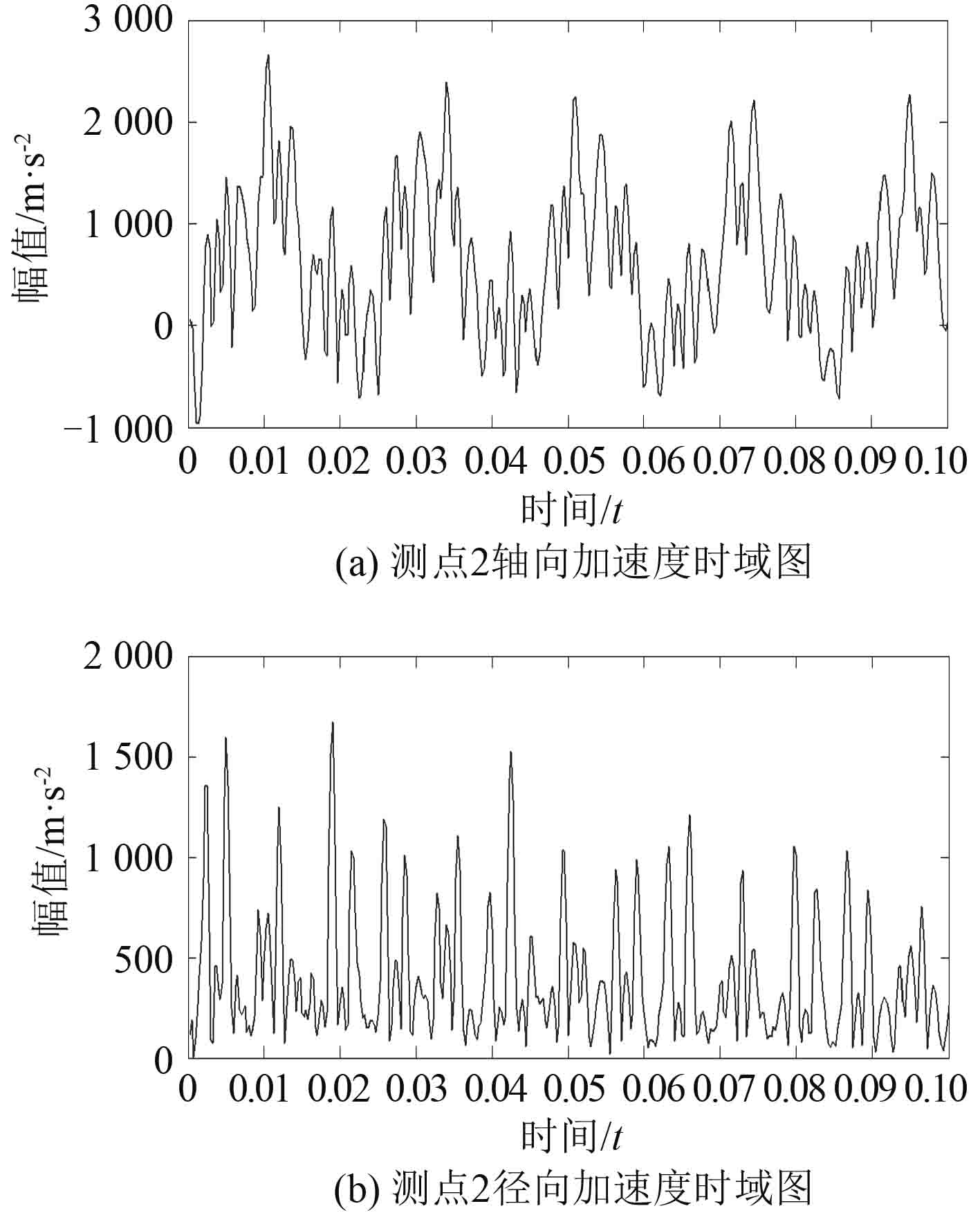
|
图 11 考虑螺栓连接的支承结构测点 2 的加速度时域图 Fig. 11 The acceleration time domain of the structure in measuring point 2 when bolt connection is considered |
分析图 8~图11 可看出,无论是整体结构还是考虑螺栓接触的结构,在同一测量方向上,测点 2 处响应信号的振幅普遍比测点 1 处要大;在同一测点处,轴向和径向测量所得加速度信号的幅值也有一定的差距,这是由于测点 1 和测点 2 处结构的刚度存在差异,同时,此次的响应仿真中,激励信号是沿轴向在弹性鼠笼上施加的。
对比同测点、同方向的加速度响应,整体结构中,激励点受到的每次冲击能够在响应点的振动信号中体现为随时间的衰减变化趋势,且波形较为明显。而在考虑螺栓连接的轴承支承结构中,由于信号的传递路径较为复杂,受到螺栓连接结构的影响,不同频率的信号在传递过程中受到的衰减,削弱程度不同,导致测得的响应信号变得较为复杂,其中,由于测点 2 离激励点较远,传递路径更为复杂,这就使得对于故障信号的提取和处理难度更大。
4 结语通过对复杂轴承支撑结构动力学特性的一系列仿真及对比分析,得到以下结论:
1) 螺栓连接结构的存在对系统模态有着较大的影响,相比而言,整体结构的各阶模态值普遍偏高;随着螺栓预紧力的增大,系统的各阶模态值也呈增大趋势,但差距并不明显。
2) 螺栓连接结构使得信号在高频处的衰减作用要更加明显,而且随着频率的不断提高,螺栓结构对信号的衰减作用越来越明显,这一特性在整体结构中是难以体现的。
3) 复杂结构设备轴承支撑结构中由于存在多处螺栓连接结构,信号从结构内部传递到机匣处需经过复杂的传递路径。当轴承故障信号从内部向外传递时,在机匣处测得的响应信号已经难以体现信号原本的特性,这在一定程度上增加了有效信号提取的难度,影响了故障诊断的准确性。
| [1] | 陈果. 含碰摩故障的新型转子-滚动轴承-机匣耦合动力学模型[J]. 振动工程学报, 2009, 22 (5): 538–535. |
| [2] | 赵帅, 王克明, 慕鹏, 等. 螺栓联接结构振动特性有限元分析方法的研究[J]. 沈阳航空航天大学学报, 2012, 29 (2): 18–22. |
| [3] | NARUSE T, SHIBUTANI Y. Nolinear bending stiffness of plates clamped by bolted joints under bending moment[J]. Journal of Solid Mechanics and Materials Engineering, 2012, 6 (7): 832–843. DOI: 10.1299/jmmp.6.832 |
| [4] | 陈长盛, 王强, 柳瑞锋, 等. 螺栓连接对结构模态及传递特性影响研究[J]. 振动与冲击, 2014, 33 (2): 178–182. |
| [5] | 赵猛, 张以都, 马良文, 等. 装配结构模态仿真与实验对比研究[J]. 振动与冲击, 2005, 2 (1): 28–30. |
| [6] | 温淑花, 张学良, 武美先, 等. 结合面法向接触刚度分形模型建立与仿真[J]. 农业机械学报, 2009, 40 (11): 197–202. |
| [7] | 温淑花, 张学良, 文晓光, 等. 结合面切向接触刚度分形模型建立与仿真[J]. 农业机械学报, 2009, 40 (12): 223–227. |
| [8] | 黄志新, 刘成柱. ANSYS Workbench14.0超级学习手册[M]. 北京: 人民邮电出版社, 2013. |
| [9] | 艾延廷, 武威, 田晶, 等. 被联接件形式对结构模态及传特性影响的研究[J]. 科学技术与工程, 2014, 14 (4): 46–50. |
 2017, Vol. 39
2017, Vol. 39
