2. 中国船舶及海洋工程设计研究院, 上海 200011
2. Marine Design and Research Institute of China, Shanghai 200011, China
船上柴油机主机造成的振动问题仍然是目前的研究重点,主机诱发产生的振动问题会直接影响到上舰的人员工作生活的环境。而针对柴油机机座的动力学模态分析对改善主机振动问题有着重要意义。目前模态分析的研究趋势是把有限元模态分析与试验模态技术相结合,通过有限元模态分析结果指导试验模态分析,而后利用试验模态分析结果检验与修正有限元模型,再利用修正后的有限元模型重新进行模态分析以及后续的频响分析等动力学计算[1-5]。然而试验模态分析所需试验设备条件复杂且花费高昂(针对不同类型与尺度的结构对应不同的试验方法),并且测定的过程中对环境(噪声等级)也有一定要求,这就使得尺寸极大的船用机座结构不适用上述理想方法进行研究与优化。而另一方面,绝大部分有限元模态分析的相关研究着重于软件的基本使用,主要论述的是有限元模型的建立与结果的输出而少有对模态参数的具体分析,更不用提针对性的结构优化[7-13]。
此外船用柴油机机座是无加强的板架结构,由于结构尺寸的限制使得加强筋的焊接较难且强度方面也无需加强,因此多是无加筋板。在这类结构的有限元模态分析中经常会出现大量的局部模态,使得计算结果具有很强的混淆性,且难以分辨。该类问题一直是结构有限元模态分析中的一个重点,一般情况是人为的对局部结构进行额外的加强,来消除局部模态,但这往往会使得结构失真,其计算结果可信度较低。并且,这种现象未必局限于船用柴油机机座结构,更是一个普遍性的结构问题。
对船用柴油机机座进行动力学分析中的另一个难题是阻尼难以确定,理想情况也是通过实验模态分析来测出每一阶模态的阻尼比,以指导有限元动力学分析的参数设置[1-4]。可见,要进行高质量的有限元模态分析严重的依赖于试验数据,而船用柴油机机座的现场试验在大多数情况下由于经费、资源、试件规模本身等多种原因很难实现,因而本文旨在充分利用有限元分析软件的功能取长避短,分别提出模态有效质量系数,以及采用虚拟梁这 2 种技巧来进行深一层的对船用机座结构进行模态分析,以期不借助于试验模态分析就能够对结构提出针对性的优化意见。
1 结构模态分析的工程意义目前,由于阻尼的复杂性,在缺乏现场试验的数据支撑下,有限元动力学分析中几乎不可能将阻尼考虑在内。因而通过假设阻尼进行各类动力学求解得到的计算结果都会有较大的偏差甚至会得到与实际情况完全不同的结论。所以进行无阻尼的结构模态分析其主要的工程意义在于得到结构的固有频率与模态振型。一是对比固有频率与设备的激励频率来预防结构共振,二来是根据模态振型来得出结构刚度薄弱的区域进行局部加强[1]。
此外利用模态之间的正交性,即从能量角度来看,不同固有模态之间在力学上相互独立[3]。因而结构在某一频率下的响应主要取决于个别主模态。所以在无法改变整体结构以错开激励频率的情况下,可以根据接近激励频率的模态振型针对性的对局部低刚度区域进行加强,能够使得结构优化工作更加针对与有效。在工期紧张,或激励条件与阻尼参数不明确的情况下,即有限元频响分析较难开展或可信度较低的时候,针对性的对个别模态的结构优化不失为一个较快捷而又相对准确的途径。
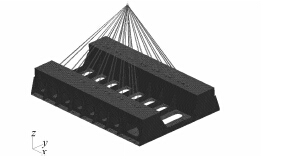
2 实例计算与分析本文选取上海海事大学自动化机舱的 MAN B&W 6S35ME-B9 型船用柴油机机座结构为实际算例。采用大型通用有限元软件 MSC.Patran/Nastran 进行无阻尼线性模态分析[4](下文所涉及的模态分析皆为无阻尼模态分析)。有限元模型采用二维板单元进行建模,同时为了考虑螺栓孔的模拟单元大小取 50 mm × 50 mm,结构材料选用碳素钢。机座结构总质量为 14.58 t,使用质量点单元模拟柴油机质量(99 t),其重心位置根据柴油机说明书进行设置(2 988,0,3 771)。有限元模型及坐标系如图 1 和图 2所示。
|
图 1 柴油机机座有限元模型(俯视) Fig. 1 A finite element model of diesel engine(Top view) |

|
图 2 柴油机机座有限元模型(仰视) Fig. 2 A finite element model of diesel engine(Upward view) |
由于刚度矩阵对模态分析的结果影响极大,因而对于约束的加载十分关键[1]。对于机座结构而言,主要考虑下表面与地面的约束,以及上表面与设备底面的约束。而这 2 种约束时常是通过螺栓确定的。在某特种车发动机支架的模态研究中[8],在建模时就考虑了螺栓孔的建模,然而文献内并未提及螺栓位置约束的设置。而对于一些大型设备或结构的相关研究[9-11],对于其下表面与机架连接的约束条件也并未进行详细的介绍。从文献的截图中一般可以看到,这些研究在约束方面一般都假设底面接触为全约束,这样做往往会使得结构底面处于过约束的状态,使得刚度矩阵失真。而另一方面,对于结构承载设备接触面的 MPC 单元,也不能仅仅将所有自由度都进行关联,这样同样会使得刚度矩阵失真。本算例中,出于最危险工况考虑,忽略设备、结构、底面之间的摩擦力造成的弱约束,取机座结构底面为z 向平动约束与zx,zy 平面内的转动约束。而在底脚螺栓孔处取全约束。而对于承载设备的上表面,在结构上表面各节点与设备质心之间建立 MPC(RBE2)单元,设置z 向平动约束与zx,zy 平面内的转动约束关联(图中未显示);而对于设备与机座连接的螺栓孔与设备质心之间同样建立 MPC 单元进行六向自由度的关联(见图 1)。
在此基础上,进行无阻尼线性模态分析,得到固有频率与模态振型云图(见表 1和图 3)。
|
|
表 1 前 10 阶固有频率(单位:Hz) Tab.1 The first 10 order natural frequency(Unit: Hz) |

|
图 3 前 10 阶模态振型云图 Fig. 3 The first 10 modal shapes |
根据计算结果显然可以看到第 3 阶至第 10 阶模态振型云图都是由于局部振型过大而使得难以观察到整体模态,并且也可能存在局部模态的情况。对比固有频率,可见第 3 阶与第 4 阶,第 5 阶至第 7 阶,第 8 阶与第 9 阶,固有频率十分接近,其中可能是 2 个模态接近,也有可能是相似结构的相对应的局部模态,这类问题在白车身的模态分析中也有类似的体现[6]。此外在多数模态分析研究中[7-13],主要的分析内容也仅局限于列举固有频率与激励频率相对比以验证满足使用需求,以及枚举整体振型以论述结构的整体刚度情况,缺少深入的分析。因而解决局部模态无法辨别以及无法提取整体模态振型等问题是有限元模态分析的一大难点,本文就此提出通过 Nastran 的高级应用功能来提取有效模态质量系数的方法进行分析。
3 辨别主要整体模态的方法有效模态质量系数能够辨识某阶模态中质量移动的方向,以及该阶模态中包含了整个结构中多少比例的质量。通过该系数能够帮助预测哪些重要的模态会对结构响应造成主要影响。其理论依据为通过假设结构整体在某一时刻的运动为一刚性体运动向量 {D}R,能够等效为一系列相互正交的结构特征向量(柔性体运动向量)的线性叠加。
| ${\{ D\} _R} = [\phi ]\{ \varepsilon \} $ |
式中:
将该式左乘
在 Nastran 求解过程中提交 MEFFMASS 命令[14],即可在输出文件中提取平动方向有效模态质量系数如表 2 所示,转动方向数据略。
|
|
表 2 有效模态质量系数(平动方向) Tab.2 Effective modal mass coefficient(Translational direction) |
表中,FRACTION 列中即为有效模态质量系数,SUM 列中代表有效模态质量系数自第 1 阶起累加之和。由于该算例中只提取了前 10 阶模态,所以 SUM 值达不到理论值 1。假定 SUM 值达到 90% 时,即可代表所求的所有模态向量已经可以充分描述任意方向的向量。该算例R3 方向(XY 平面内的转动)为 89.5%,这里近似视为 90%。另外,表中对在某一运动方向上占主要因素的阶数进行了深色标注。若 SUM 值达不到 90%,即说明所计算的模态阶数不足以完全描述结构在各个自由度上的振型特点,因此需要另外增加特征根求解的个数。
综上所述,第 1 阶,2 阶,5 阶分别为 6 个自由度方向上的主要模态,而其余模态即可以认为是局部模态,其对总体结构的响应的影响极小,因而可以忽略不计。并且,可证第 1 阶模态主要影响整体结构在T2,R1,R3 方向上的响应(Y 方向平动,YZ 平面,XY 平面转动);第 2 阶模态主要影响整体结构在T1,R2 方向上的响应(X 方向平动,XZ 平面转动),第 5 阶模态主要影响整体结构在T3,R3 方向上的响应(Z 方向平动,XZ 平面转动),其中R2 方向的响应第 2 阶模态会起到 63.6% 的影响,而第 5 阶模态会起到 34.8% 的影响。简而言之,就是若要控制R2 方向上的响应变形,就要同时针对第 2 阶和第 5 阶的模态进行优化。
由于各类阻尼对结构特征根方程求解的影响较小[1-2],对模态结果影响甚微,因此即使在缺少阻尼数据的情况,就能针对性的根据结构所受到的激励方向来对结构进行后续的优化。而无需详细的试验模态分析来求解阻尼系数,再进行频响,瞬态等耗时耗资源的动力学计算。
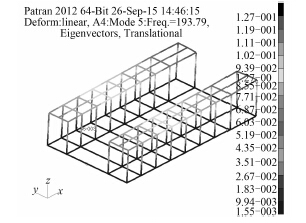
4 提取整体模态振型的方法由第 3 节可以确定第 5 阶模态应该为一整体模态,然而依然不能得到整体模态振型。这主要是由于刚度分布极不均匀的大面积不加筋板局部位移远大于整体位移。即刚度相对极弱的板中央的单元位移就远大于刚度较大的整体结构。针对该问题文本提出一种“虚拟梁”的小技巧(见图 4)。
|
图 4 用虚拟量显示第 5 阶模态振型 Fig. 4 Display fifth order mode shapes by using virtual quantity |
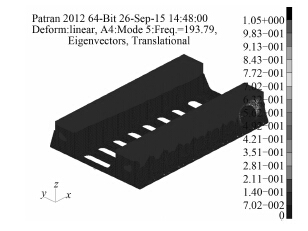
主要做法是在结构刚度较大的板材连接处建立了两节点的梁单元,该梁单元的剖面大小近似为 0,因而可近似一无质量无刚度的附加结构,且不会对实际结构产生任何力学性能的影响,所以在此称为虚拟梁单元。该虚拟梁的变形能够等效为梁两端节点间的相对变形,若提取出所有虚拟梁单元的变形云图,从而就能够直观得到系统中各个结构关键点之间的相对位移变化,从而得到整体振型(见图 5)。而对于该机座结构,结构关键点即是多块板材的公共边的交接处,由于是多个方向板材的连接位置,从而在个方向上都具有较大的刚度,所以最能体现整体的变形。在 Patran 后处理时显示梁元的变形即可[4]得到该阶模态下的整体振型。
|
图 5 板单元显示第 5 阶模态振型 Fig. 5 The plate element shows fifth order modes |
由上组对比也可看到,整体结构的最大相对位移为 0.127 mm,而对于板件的最大相对位移会达到 1 mm,两者相差将近 10 倍,因而不做任何处理,在有限元云图显示中很难观察到整体结构的变形。
5 结语目前大多有限元模态分析的研究只停留在软件基本应用层面得出计算结果而缺乏对数据特性的对比分析与筛选。另一方面,船用柴油机机座结构是无加强的板架结构,非常容易产生本文算例中出现的局部模态难以辨识,整体振型难以提取等问题。本文使用大型通用有限元软件 MSC.Patran/Nastran,以上海海事大学自动化机舱的 MAN B&W 6S35ME-B9 型船用柴油机机座结构为实际算例,提出了 2 种计算结果分析技巧以提升对模态分析计算结果的利用,能够更加深入对计算结果的分析。对计算结果进一步的提炼,对船用柴油机机座结构优化工作减少船上振动起到更为针对性的辅助作用。
1) 在结构有限元建模时,对比参照了类似研究,分别对柴油机机座结构与地面以及结构与设备相互的接触面约束,以及螺栓位置的约束进行不同的处理。以更真实的模拟结构的刚度矩阵。
2) 通过 Nastran 的高级功能能够提取有效模态质量系数,通过该系数,一方面可以通过质量系数的累加总数来判断当前求解阶数是否得到了所有的主要模态向量。另一方面可以筛选出质量系数较大的模态,以此剔除求解过程中得到的局部模态。此外还可以通过每一阶模态在各个自由度方向上所占的质量系数来判断单一方向的自由度与哪几阶模态有直接关系。
3) 通过在结构关键点建立虚拟量单元的方法,以提取整体模态振型,从而避免由于板材中部低刚度点的个别大位移变形影响整体云图的显示。
4) 对于该船用柴油机机座结构计算可得,第 1 阶,第 2 阶,第 5 阶模态为结构的 3 个主模态,在各个方向上占到了模态有效质量系数的 90% 以上。因而只要针对该 3 阶模态在其主导的自由度方向上进行结构优化,就能针对主机激励方向而显著的改善主机向船体传递的振动问题。
5) 本文的不足之处在于,算例中的船用机座是安置在地面上,因此与直接安置在船上的船用机座在约束条件上略有不同,若要对船上的柴油机机座进行相关分析还需更多的考虑机舱结构的耦合作用。
综上所述,通过本文的 2 个分析技巧,在没有资源与能力条件进行试验模态对有限元模态分析进行综合评价与调整的情况下,提出了一种针对船用主机模态分析的新思路,能够更加深入的进行分析有效的将有限元计算数据提取并加以利用。该算例得出的计算结果以及计算方法还能扩展为同类型的机座结构进行针对性的动力学优化计算。
| [1] | 曹树谦, 张文德, 萧龙翔. 振动结构模态分析--理论, 试验与应用[M]. 天津: 天津大学出版社, 2014. |
| [2] | ROBERT E C (美). 试验结构动力学[M]. 北京: 清华大学出版社, 2012. |
| [3] | 长送昭男(日). 声振模态分析与控制[M]. 北京: 科学出版社, 2014. |
| [4] | 田利思. MSC NASTRAN动力分析指南[M]. 北京: 中国水利水电出版社, 2012. |
| [5] |
龙英, 腾召金, 赵福水. 有限元模态分析现状与发展趋势[J]. 湖南农机, 2009, 4 (36): 27–28.
LONG Ying, TENG Zhao-jin, ZHAO Fu-shui. The present status and development trends of finite element modal analysis[J]. Hunan Agricultural Machinery, 2009, 4 (36): 27–28. |
| [6] |
曹妍妍, 赵登峰. , 有限元模态分析理论及其应用[J]. 机械工程与自动化, 2007, 140 (1): 73–74.
CAO Yan-yan, ZHAO Deng-feng. Finite element modal analysis theory and its application[J]. Mechanical Engineering & Automation, 2007, 140 (1): 73–74. |
| [7] |
刘向东, 庞福振. 船用主机基座系统的振动特性研究[J]. 造船技术, 2009 (3): 35–40.
LIU Xiang-dong, PANG Fu-zheng. Study on vibration characteristics of main engine system for ship[J]. Shipbuilding Technology, 2009 (3): 35–40. |
| [8] |
艾松树, 周照耀, 邵明. 特种车辆发动机支架模态分析[J]. 现代制造工程, 2004 (10): 42–44.
AI Song-shu, ZHOU Zhao-yao, SHAO Ming. Modal analysis of special vehicle engine support[J]. Modern Manufacture Engineering, 2004 (10): 42–44. |
| [9] |
刘金玲, 金涛, 马宇山. 柴油机整体有限元模态分析[J]. 机械工程师, 2009 (8): 84–85.
LIU Jin-lin, JIN Tao, MA Yu-shan. The holistic finite element model analysis of diesel engine[J]. Mechanical Engineer, 2009 (8): 84–85. |
| [10] |
梅德庆. 280MW汽轮机基座振动特性的模型试验[J]. 动力工程, 2005 (5): 652–655.
MEI De-qing. Research on vibration characteristics of a 280 MW steam turbine-generator foundation by model testing[J]. Power Engineering, 2005 (5): 652–655. |
| [11] | 张洋, 数控铣床工作台预紧与其动态特性关系的研究[D]. 沈阳:沈阳工业大学, 2011. |
| [12] | 郭云春, 螺栓连接镁车架的有限元分析与结构优化[D]. 重庆:重庆大学, 2012. |
| [13] |
赖兴华. 露天旋转钻机底架有限元分析及改进研究[D]. 昆明:昆明理工大学, 2010.
LAI Xing-hua. Finite element analysis and Improvement research for chassis of the open-air rotary drilling rig[D]. Kunming:Kunming University of Acience and Technology, 2010. |
| [14] | MSC, Dynamic analysis user's guide 2014, www.mscsoftware.com, 2014 |
 2017, Vol. 39
2017, Vol. 39
