声隐身性能是潜艇生存力的重要保证。潜艇内部存在复杂的管路系统,由于管路转弯、变截面等原因,流体介质在管路传输过程中会激起管路振动,进而激起艇体振动并向外辐射噪声,从而降低潜艇的隐蔽性。因此,有必要对管路系统的振动规律进行深入研究,探求能够有效控制管路系统振动噪声的技术或措施,这对于实际潜艇管路系统声学分析和优化具有重要的实际指导意义。
文献[1]使用振动分析仪采集施加各阻尼措施后圆管末端的速度信号,得到实验振动的频域波形并分析,认为阻尼材料厚度越厚、长度越长,阻尼效果越好,并提出了最优厚度。文献[2]对管路阻尼胶带抑振效果进行了公式计算和抑振效果试验,认为阻尼胶带在高频段(800 Hz ~ 8 kHz)抑振效果明显。文献[3]应用管路振动试验测试结论,证明在管路中非金属阻尼结构与挠性接管具有相当的减振效果。文献[4]阐述了橡胶的动态力学特性和水声特性,并分析了橡胶应用于水下声隐身技术特别是管道隔振和减振的理论基础。文献[5]对管路表面阻尼处理进行了详细的理论分析,推导出管路阻尼处理后结构损耗因子计算公式,并计算出 SA-3 阻尼材料的结构损耗因子,认为这种材料高阻尼温度区正好符合潜艇工作温度,减振效果明显。
上述文献仅针对孤立管路进行了阻尼材料的减振效果分析,还缺少对管路与潜艇壳体水下流固耦合声场的研究,为更接近潜艇水下实际状态,本文选取圆柱壳这一潜艇典型结构,在其内部设置简单管路,并对管路与圆柱壳水下的振动与声学特性进行研究。
鉴于结构有限元耦合流体边界元算法针对解决流固耦合问题和预报圆柱壳水下振动与声辐射的有效性得到了较好的验证[6-9],因此,本文以内部设有管路的圆柱壳结构作为研究对象,采用结构有限元耦合流体边界元算法,针对管路内、外敷设不同厚度橡胶层时,圆柱壳结构的振动与声学特性进行数值研究,从圆柱壳结构振动位移和辐射噪声 2 个方面探讨管路内、外敷设橡胶层对圆柱壳水下振动与声辐射的影响。
1 结构有限元耦合流体边界元算法水下结构振动与声辐射是流体与结构相互作用的流固耦合过程。假设流体理想无粘性,无旋,c0 为流体声速,k 为波数,ω 为角频率。
采用有限元方法对方程进行数值离散,考虑到稳态响应问题,可以得到:
| $\left[ {{\mathit{\boldsymbol{K}}}_{s}}-{{\omega }^{2}}{{\mathit{\boldsymbol{M}}}_{s}}-i\omega {{\mathit{\boldsymbol{N}}}_{s}} \right]\mathit{\boldsymbol{a}}=\mathit{\boldsymbol{F}}+{{\mathit{\boldsymbol{F}}}_{\rm{out}}},\text{,} $ | (1) |
式中: Ms, Ns, Ks 分别为结构的质量矩阵,阻尼矩阵,刚度矩阵; a 为节点位移幅值; F 为直接作用在结构上的节点力; Fout 为外域流体作用于结构湿表面的等效节点力。
| $ {{\mathit{\boldsymbol{F}}}_{out}} = \left[ { - \left( { - {\omega ^2}{\mathit{\boldsymbol{ M}}}} \right) - \left( { - {\mathit{\boldsymbol{i}}}\omega {\mathit{\boldsymbol{ N}}}} \right)} \right]{\mathit{\boldsymbol{a}}}\text{,} $ | (2) |
式中 M 和 N 分别为外域流体对结构的附加质量和附加阻尼矩阵。将式(2)代入方程(1),得到最终的流固耦合方程为:
| $ \left[ {{{\mathit{\boldsymbol{ K}}}_s} - {\omega ^2}({{\mathit{\boldsymbol{ M}}}_s} + {\mathit{\boldsymbol{ M}}}) - {\mathit{\boldsymbol{i}}}\omega ({{\mathit{\boldsymbol{ N}}}_s} + {\mathit{\boldsymbol{ N}}})} \right]{\mathit{\boldsymbol{a}}} = {\mathit{\boldsymbol{F}}}\text{,} $ | (3) |
求解方程(3)即可求得湿表面振动位移向量,进而利用公式[9]
| $ W = \frac{1}{2}Re\{ i\omega \sum\limits_{j = 1}^{{m_e}} {{p_j}\delta _j^*{S_j}} \} \text{,} $ | (4) |
| $ < \overline {{V^2}} > = \frac{{{\omega ^2}\sum\limits_{j = 1}^{{m_e}} {\left| {{\delta _j}} \right|{S_{\rm{j}}}} }}{{\sum\limits_{j = 1}^{{m_e}} {{S_{\rm{j}}}} }} \text{,}$ | (5) |
得到结构的辐射声功率W 和结构表面的均方法向速度
| $ {L_W} = 10\lg \frac{W}{{{W_{ref}}}}\text{,} $ | (6) |
| $ {L_{\bar V}} = 10\lg \frac{{ < {{\bar V}^2} > }}{{V_{ref}^2}}\text{。} $ | (7) |
计算得到湿表面的声功率级,均方法向速度级,式中Wref = 10-12 W,Vref = 5 × 10-8 m/s。
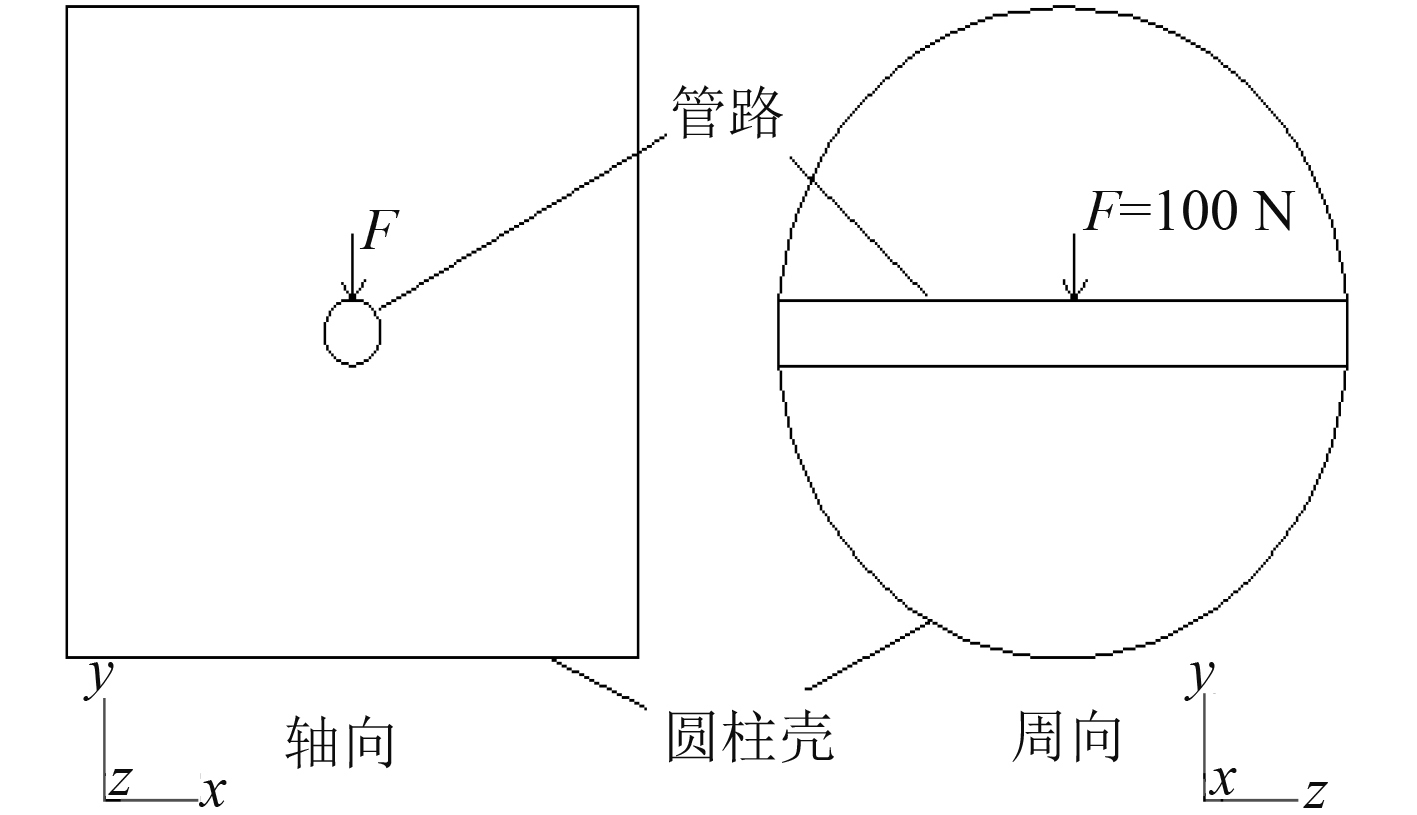
2 几何模型及有限元建模本文研究所采用的结构模型如图 1 所示,其中圆柱壳结构用于模拟潜艇舱段,管路水平布置于圆柱壳正中部,管路与圆柱壳之间采用刚性连接。结构模型具体尺寸如表 1 所示。
|
图 1 圆柱壳与管路基本结构 Fig. 1 Fundamental structure of the cylindrical shell and pipeline |
|
|
表 1 圆柱壳结构参数 Tab.1 Parameters of the cylindrical shell |
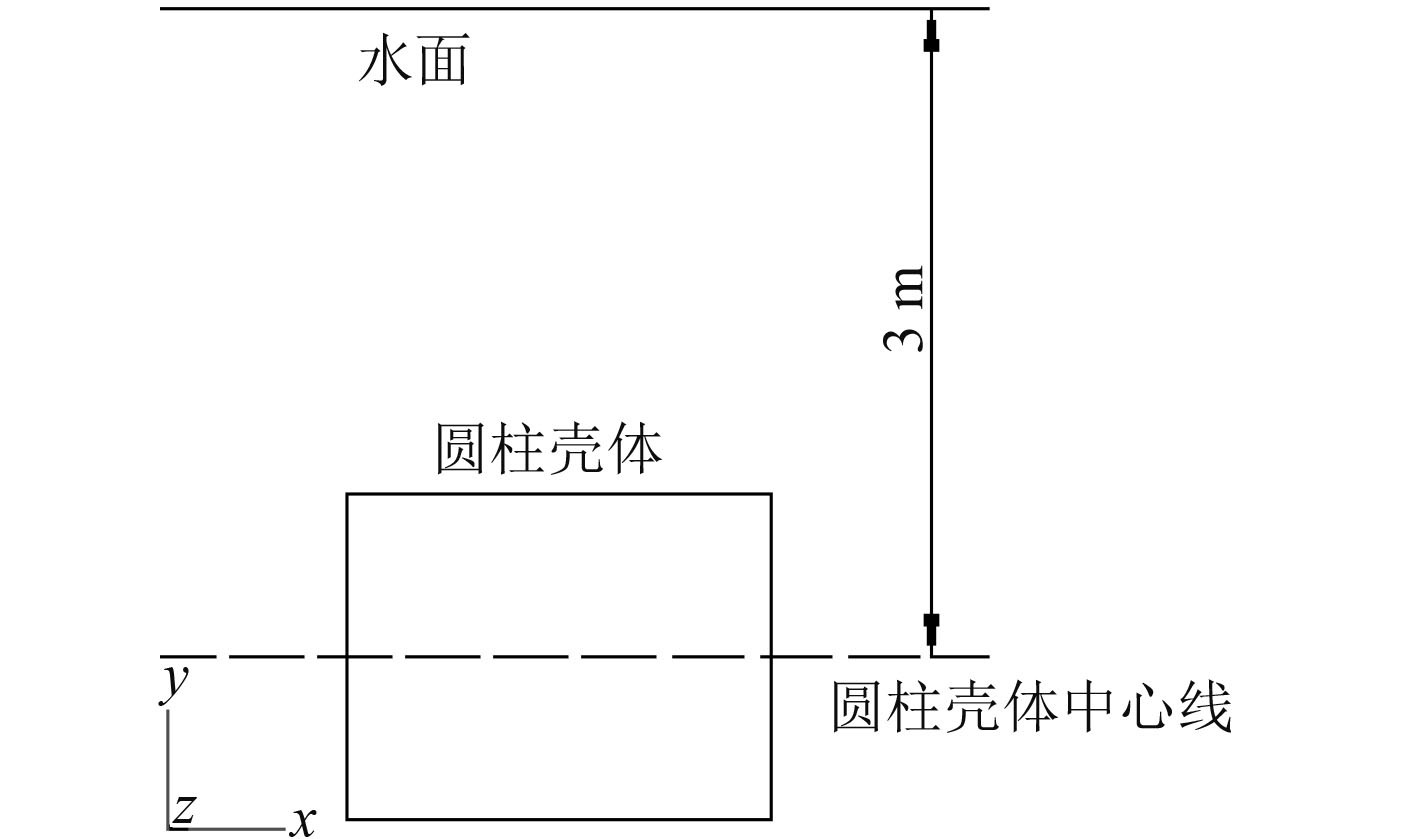
敷设橡胶层前后,幅值为 100 N 的激振力始终作用在附钢材属性的管路上表面的中心节点上,加力点为y 轴负方向(竖直向下),圆柱壳体中心距离水面 3 m(见图 2)
|
图 2 圆柱壳体在水下的位置 Fig. 2 Location of underwater cylindrical shell |
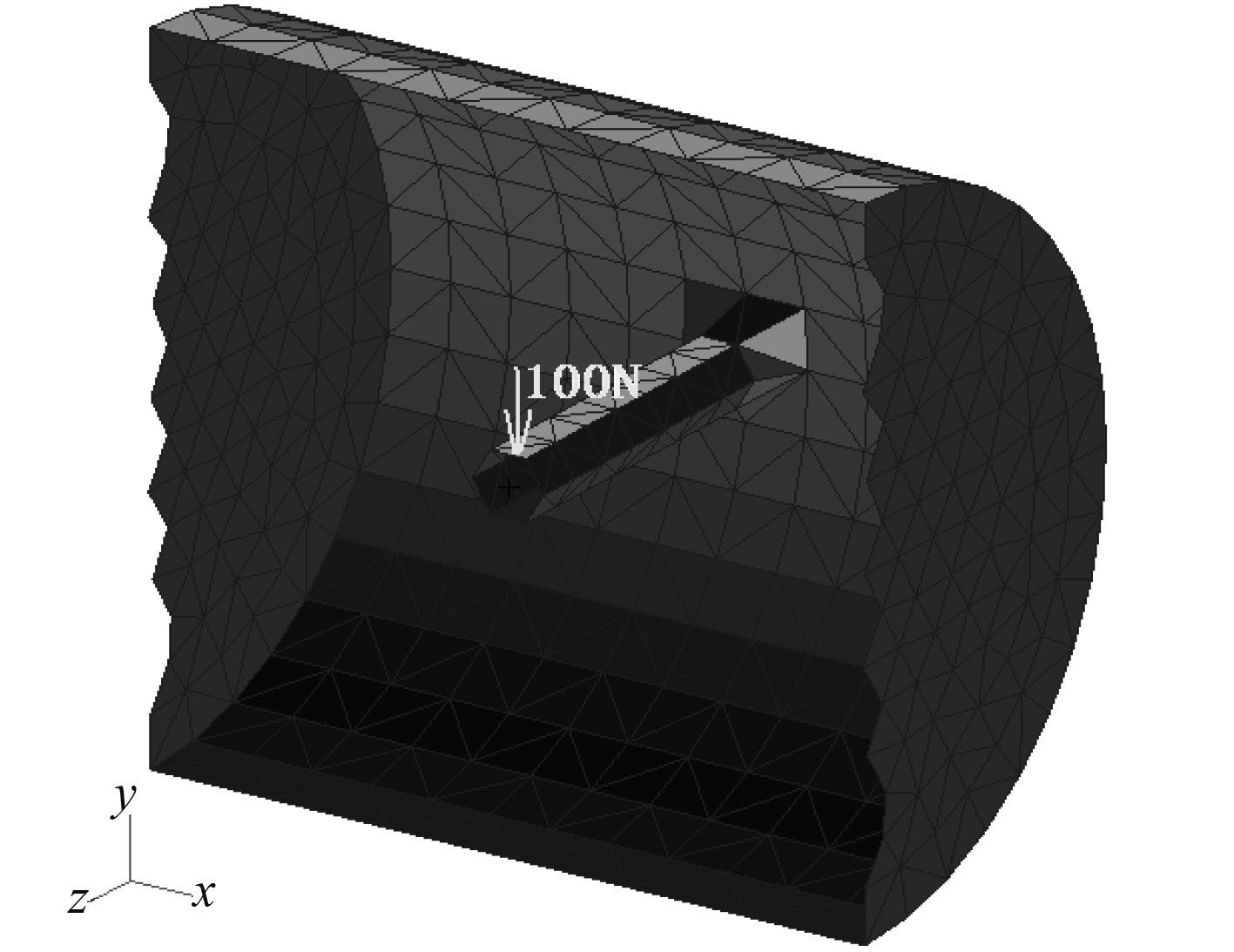
利用 MSC.PATRAN 软件对内部设有简单管路的圆柱壳进行有限元建模,如图 3 所示。模型选用三节点三角形壳单元,圆柱壳单元附钢材属性,无橡胶层的管路单元附钢材属性,敷设橡胶层的管路单元附钢材与橡胶结合的复合材料属性。材料属性见表 2。
|
图 3 结构有限元模型剖面图 Fig. 3 Structural FE model profile |
|
|
表 2 材料属性 Tab.2 Material property |
针对橡胶层敷设位置及厚度的不同,建立了 5 种不同的有限元模型,用于计算分析,如表 3 所示。
|
|
表 3 五种计算模型 Tab.3 Five calculation models |
针对 5 种不同的有限元模型,采用相同的激振力,进行了水下圆柱壳结构振动与辐射声场的仿真计算,激振频率为 50 ~ 990 Hz,步长 10 Hz。计算边界为自由边界,考虑水面反射的影响,流体密度为 1 020 kg/m3,流体中声速为 1 450 m/s。
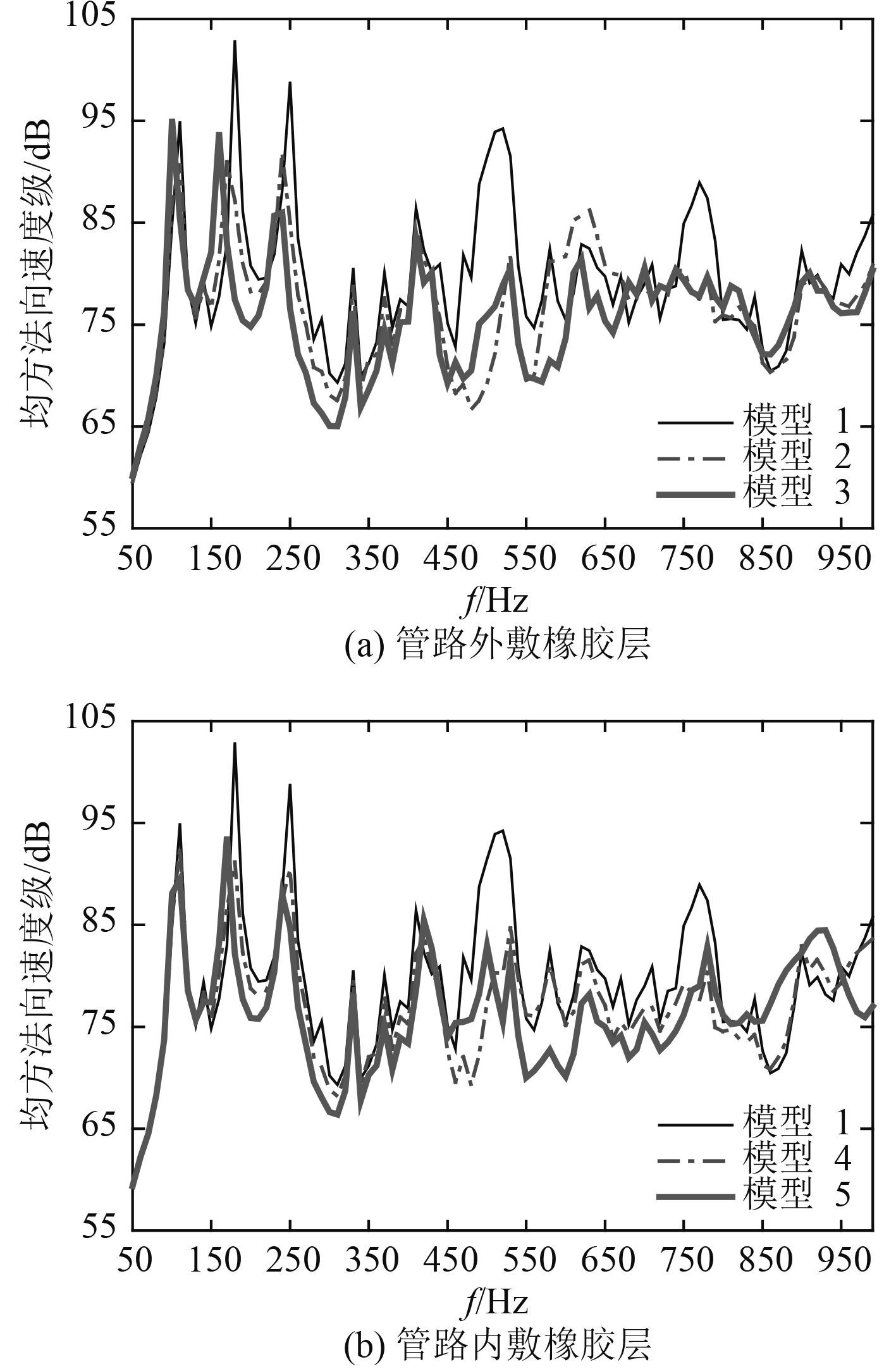
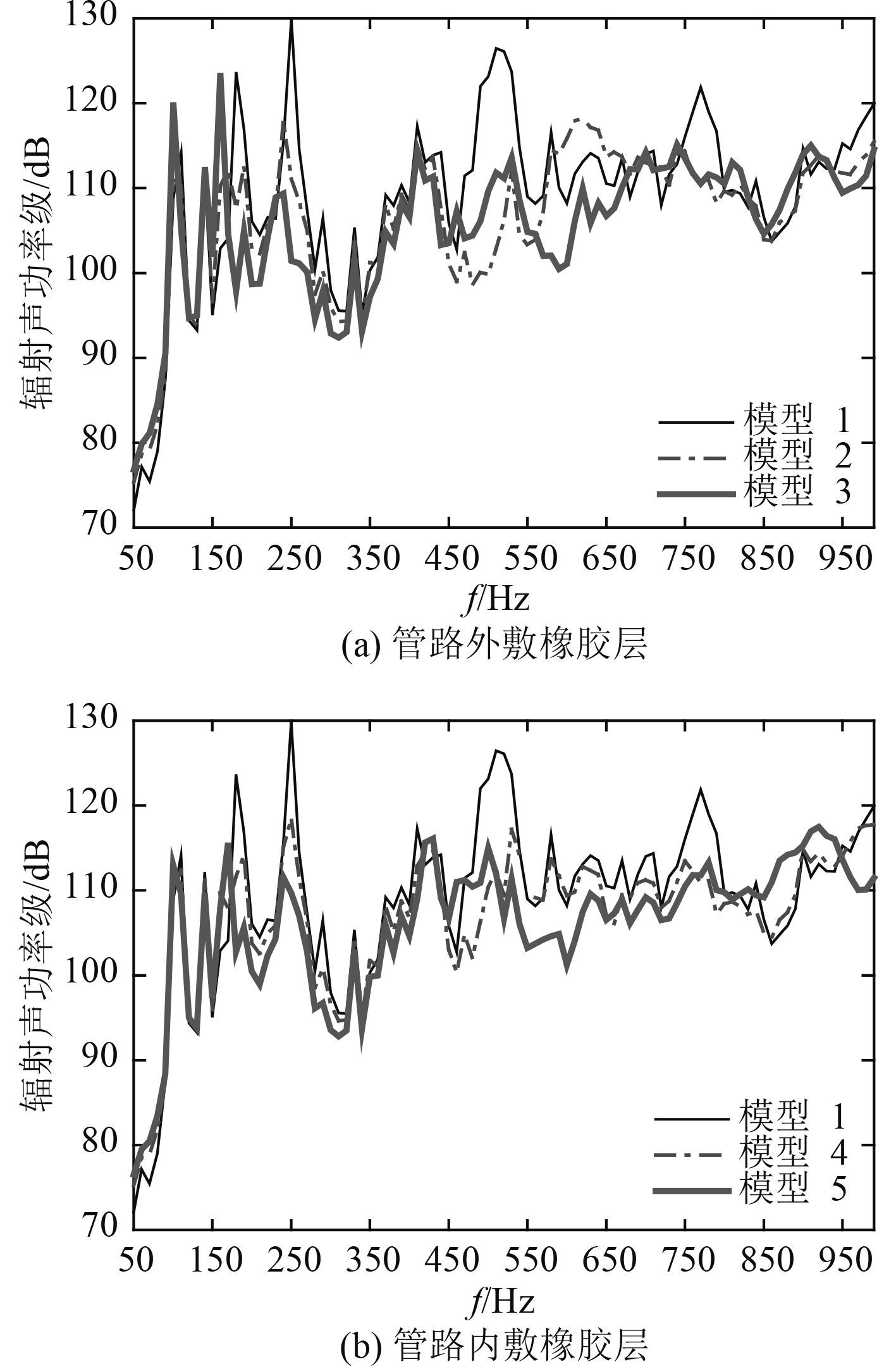
图 4 和图 5 分别为 5 种模型圆柱壳湿表面的均方法向速度级频响曲线和辐射声功率级频响曲线。
|
图 4 圆柱壳湿表面均方法向速度级频响曲线 Fig. 4 Mean-square normal velocity level frequency response curves of cylindrical shell wetted surface |
|
图 5 圆柱壳湿表面辐射声功率级频响曲线 Fig. 5 Radiated acoustic power level frequency response curves of cylindrical shell wetted surface |
从图 4 和图 5 可看出:与模型 1 相比,在 180 Hz 时,模型 2 ~ 模型 5 的圆柱壳湿表面的均方法向速度级的减小量分别为 15.8 dB,25.5 dB,11.7 dB,20.8 dB;在 250 Hz 时,模型 2 ~ 模型 5 的圆柱壳湿表面的辐射声功率级的减小量分别为 18.8 dB,28.5 dB,11.4 dB,20.7 dB。在整个计算频率范围内,与模型一相比,管路内、外敷设橡胶层后,圆柱壳湿表面的均方法向速度级和辐射声功率级都有不同程度地减小,尤其是在几个峰值频率附近最明显。管路敷设的橡胶层越厚,圆柱壳湿表面均方法向速度级和辐射声功率级减小量越大,对圆柱壳结构的减振和降低辐射噪声效果越好。
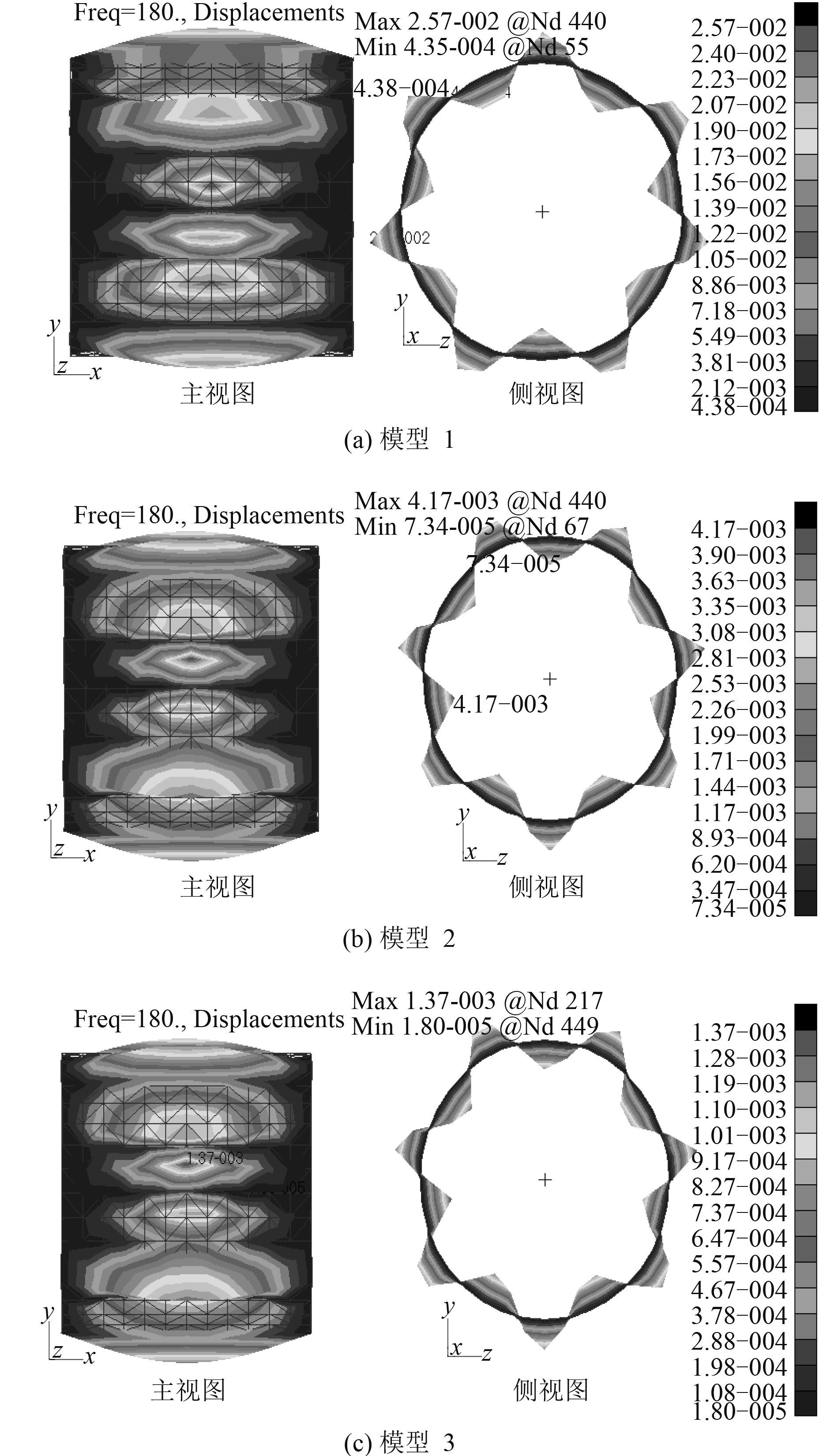
从图 5 可看出,模型 1 圆柱壳湿表面均方法向速度级在 180 Hz 时达到峰值。因此,对模型 1 ~ 模型 3 在 180 Hz 时圆柱壳(不含端盖)湿表面的位移云图进行对比,如图 6 所示。从图中可知:与模型 1 相比,管路敷设橡胶层的圆柱壳湿表面对应位置的位移较小。橡胶层越厚,圆柱壳湿表面对应位置的位移越小。模型 2 圆柱壳湿表面最大位移是模型 1 圆柱壳湿表面最大位移的 1/6。模型 3 圆柱壳湿表面最大位移是模型 1 圆柱壳湿表面最大位移的 1/19。
|
图 6 圆柱壳湿表面位移云图 Fig. 6 Displacement coutours of cylindrical shell wetted surface |
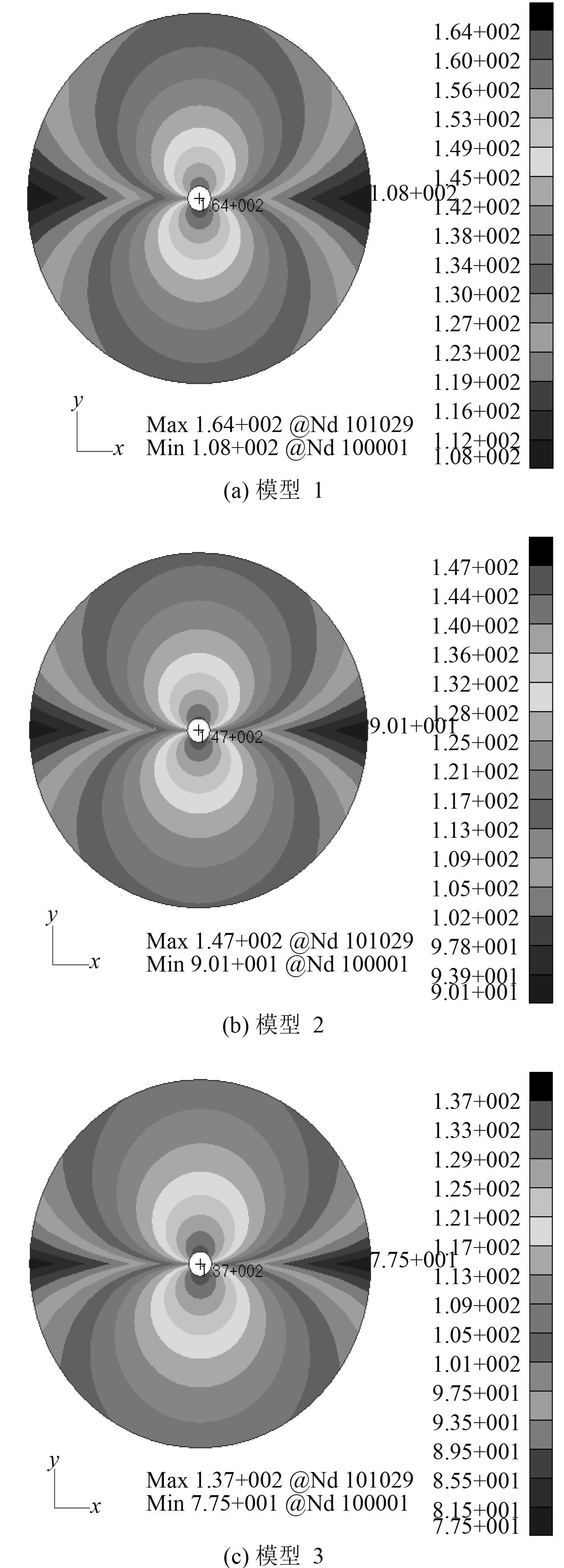
以有限元模型的中心为圆心,建立有限元声场,声场外径为 30 m,内径为 2 m,计算得到模型 1 ~ 模型 3 在 180 Hz 时的圆柱壳辐射声场声压级云图,如图 7 所示。
|
图 7 圆柱壳辐射声场声压级云图 Fig. 7 Radiated pressure coutours of acoustic filed out of cylindrical shell |
与模型 1 相比,管路敷设橡胶层的圆柱壳辐射声场中对应点的声压级减小。橡胶层越厚,辐射声场中对应点的声压级越小。
模型 2 圆柱壳辐射声场最大声压级比模型 1 圆柱壳辐射声场最大声压级减小了 17 dB,模型 3 圆柱壳辐射声场最大声压级比模型 1 圆柱壳辐射声场最大声压级减小了 27 dB。
4 结 语数值研究结果表明:就本算例而言,管路内、外敷设橡胶层对圆柱壳结构的减振和降低圆柱壳辐射噪声起到了良好的作用。与管路未敷设橡胶层的圆柱壳结构相比,管路内、外敷设橡胶层的圆柱壳湿表面的均方法向速度级、辐射声功率级和圆柱壳湿表面对应位置的位移以及圆柱壳辐射声场对应点的声压级都有不同程度的减小。
之前学者仅针对孤立管路进行了阻尼材料的减振效果分析,还缺少对管路与潜艇壳体水下流固耦合声场的研究,为了更接近潜艇水下实际状态,本文选取了圆柱壳这一潜艇典型结构,在其内部设置了简单管路,并对管路与圆柱壳水下的振动与声学特性进行了研究。在实际管路布置中要控制好敷设厚度,并解决内部敷设的技术问题。
本文为内部管路特性变化对潜艇壳体水下的振动与声学特性研究提供了一种思路,探求了有效控制管路系统振动噪声的措施,对于潜艇水下的声学结构优化具有重要的意义。为了更贴近实际情况,下一步将针对内部含复杂管路及其他强力构件的结构进行水下振动和声学特性研究,将有意义的结论向工程实践推广。
| [1] | 王仲, 陈长征, 孔祥军. 阻尼对水泵管路隔振系统的影响研究[J]. 重型机械, 2015 (1): 59–62. |
| [2] | 王育平, 张丹才, 余永丰. 通海系统管路阻尼处理降噪技术研究[J]. 噪声与振动控制, 2010, 30 (4): 40–43. |
| [3] | 梁向东, 付爱华. 非金属阻尼与挠性接管在管路减振中的作用[J]. 振动与噪声控制, 2004 (6): 18–21. |
| [4] | 张彩坤, 岳海. 橡胶在水声隐身技术中的应用[J]. 橡胶资源利用, 2007 (3): 3–6. |
| [5] | 杜冬菊, 刘爱华, 黄佳典. 阻尼减振在潜艇管路上的应用研究[J]. 中国修船, 2004 (1): 14–16. |
| [6] | 刘帆, 周其斗, 纪刚, 等. 纵桁分布方式对结构振动与声辐射的影响[J]. 兵器装备工程学报, 2006 (1): 142–146. |
| [7] | ZHOU Q, ZHANG W, JOSEPH P F. A new method for determining acoustic added mass and damping coefficients of fluid-structure interaction, in:Y. S. Wu, et al (Eds), The Eighth International Symposium on Practical Design of Ships and Other Floating Structures, Elsevier, Amsterdam, 2001, pp. 1185-1195. |
| [8] | ZHOU Q, JOSEPH P F. A numerical method for the calculation of dynamic response and acoustic radiation from an underwater structure[J]. Journal of Sound and Vibration, 2005, 283 (3/5): 853–873. |
| [9] | 纪刚, 张纬康, 周其斗. 静水压力作用的水下结构振动及声辐射[J]. 中国造船, 2006, 47 (3): 37–44. |
 2017, Vol. 39
2017, Vol. 39
