2. 船舶振动噪声重点实验室, 湖北 武汉 430060
2. National Key Laboratory on Ship Vibration and Noise, Wuhan 430064, China
随着造船技术的迅速发展,噪声问题日益受到重视,舱室噪声控制就显得尤为迫切。在船舶舱室空气噪声控制中,吸声材料被广泛应用。吸声材料可分为多孔吸声材料和共振吸声结构,多孔吸声材料以吸收中高频噪声为主,共振吸声结构在低频段吸声性能较好。为兼顾高、低频吸声效果,往往采用多孔吸声材料与共振吸声结构组成的复合结构[1-3]。在噪声控制的实际应用中,不同噪声环境降噪要求不同,噪声峰值频率亦不相同。同时,舱室敷设材料的空间和舱壁承重也有限制,如何根据噪声频谱,重量及空间的限制,选取适宜的结构参数,达到最佳的吸声效果成为亟待解决的问题。对此,复合吸声材料吸声系数理论计算研究尤为必要。目前复合吸声材料理论计算的研究取得一些成果:赵晓丹[4] 采用传递矩阵法研究空腔与薄板结构叠加问题,刘秀娟等[5]尝试用声学软件和穿孔原理计算非等厚空腔穿孔结构,而对于多层穿孔板与多孔材料的叠加结构,有学者采用声-电类比原理推导出多层复合材料吸声系数[6-7]。而对由穿孔板,多孔材料,空腔组成的多层复合结构,采用传统的声-电类比法计算忽略了本层多孔吸声材料对传播透过该层的声波的吸声作用。本文依据现有的穿孔板理论、多孔材料吸声原理,考虑这部分吸声,在传统的声-电类比法的基础上提出了一种改进计算方法,利用该方法可分析复合吸声材料各参数对吸声系数的影响。为在实际应用中针对特定吸声频带要求设计复合吸声材料结构参数提供理论依据,实现舱室空气噪声的较佳控制。
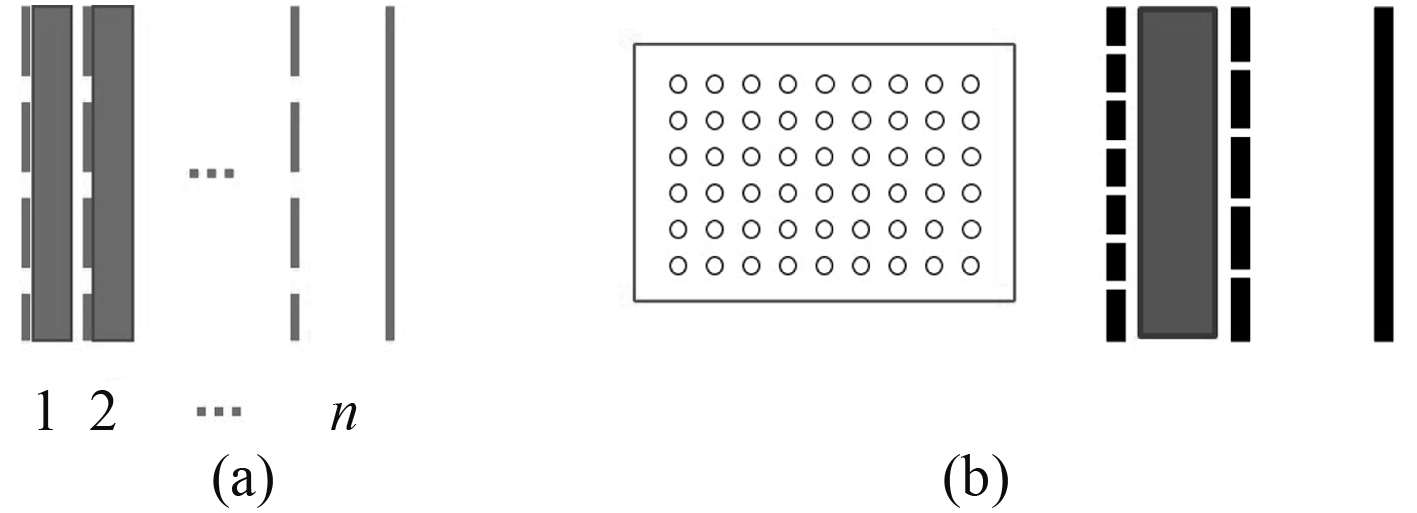
1 多孔吸声材料、穿孔板声阻抗复合吸声结构多由穿孔板,多孔材料以及空腔组成,其一般结构如图 1(a)所示。复合吸声结构声阻抗由子结构声阻抗构成。
|
图 1 复合吸声结构视图 Fig. 1 Composite sound absorption structure view |
多孔吸声材料是通过空气与材料、材料与材料之间摩擦生热消耗声能,其内部具有大量细管、缝隙、孔隙等,根据瑞丽模型,多孔材料声阻抗为[8]:
| $ {\rho _n} = \frac{N}{\delta }{\rho _O} - i\frac{{{R_n}}}{\omega }\text{,} $ | (1) |
| $ {\delta _n} = 1 - \frac{{{\rho _n}}}{{{\rho _{nm}}}}\text{,} $ | (2) |
| $ {k_n} = \frac{{{K_{nT}}}}{{{\delta _n}}}\text{,} $ | (3) |
| $ {K_{nT}} = \gamma {P_0}{\left[ {1 + \left( {\gamma - 1} \right)\frac{2}{{{k_n}\sqrt { - i} }}\frac{{{J_1}\left( {d\sqrt { - i} } \right)}}{{{J_0}\left( {d\sqrt { - i} } \right)}}} \right]^{ - 1}}\text{,} $ | (4) |
| $ {J_0}\left( x \right) \approx 1 - \frac{{{x^2}}}{4} + \frac{{{x^4}}}{{192}}\text{,} $ | (5) |
| $ {J_1}\left( x \right) \approx \frac{x}{2}\left( {1 - \frac{{{x^2}}}{2} + \frac{{{x^4}}}{{192}}} \right)\text{。} $ | (6) |
式中:ρn 为第n 层多孔材料等效密度,ρnm 为多孔材料原材料密度。kn 为波数,N 为结构常数,孔无规则分布时,取为 3;δ 为孔隙率;R 为流阻率;a 为纤维半径;P0 = 1.01 × 105 Pa 为大气压力;ρ0 = 1.295 kg/m3 为空气密度;γ = 1.4 为空气的定压比热与定容比热之比;
第n 层多孔材料特性阻抗公式为:
| $ {Z_{pcn}} = {\rho _n}{c_n}\text{,} $ | (7) |
第n 层空腔声阻抗为[7]:
| $ {Z_{cn}} = {\rho _n}{c_n}\coth \left( {i{k_n}{l_n}} \right)\text{。} $ | (8) |
式中:ln 为空腔厚度,空腔内为多孔材料,取多孔材料声阻特性值,若为空气,取ρ0,c。
1.2 复合吸声材料中第n 层穿孔板声阻抗:当复合吸声材料中第n 层穿孔板孔径为毫米级时(大于 1 mm),据 C.Zwikke 和 C.W.Kosten 研究,可当粗管情况计算,此时穿孔的声阻抗率为[9]
| $ {Z_{pn}} = i\omega {\rho _0}t + \frac{2}{d} \cdot t\sqrt {2\omega \eta {\rho _0}} \left( {1 + i} \right)\text{。} $ | (9) |
由于空气出入穿孔管时一部分声波产生摩擦损失,根据 U.Ingard 的计算[10],声阻率增加
| $ {\beta _0} = \frac{8}{{3\pi}}\left( {1 - \frac{5}{4}\sqrt \sigma + \frac{{{\sigma ^2}}}{4}} \right)\text{。} $ | (10) |
由式(9)和式(10)可得穿孔板声阻抗为:
| $ \begin{array}{l} {Z_{pn}} = \displaystyle\frac{{i\omega }}{\sigma }[{\rho _0}t + \frac{d}{2}{\beta _0}\left( {{\rho _0} + {\rho _1}} \right)] + \frac{{\sqrt {2\omega \eta {\rho _0}} }}{\sigma } \times \\[8pt] \;\;\;\;\;\;\;\;\;\;\;\left[ {\displaystyle\frac{{2t}}{d} \cdot \left( {1 + i} \right) + \frac{1}{2}\left( {1 + \frac{{\sqrt {{\rho _1}} }}{{\sqrt {{\rho _0}} }}} \right)} \right]\text{。} \end{array} $ | (11) |
式中:σ 为穿孔率;t 为板厚;d 为穿孔直径。
2 改进声电类比法及复合材料吸声系数 2.1 复合材料声阻抗计算以双层穿孔板,多孔材料,以及空腔组成的复合吸声结构为例,计算吸声系数,并分析改进声电类比法与传统声电类比法的不同,其结构如图 1(b)所示。计算采用钢板(1.0 mm),及密度为 9 kg/m3 泡沫多孔材料(流阻率为 4 800 Ns/m4)。
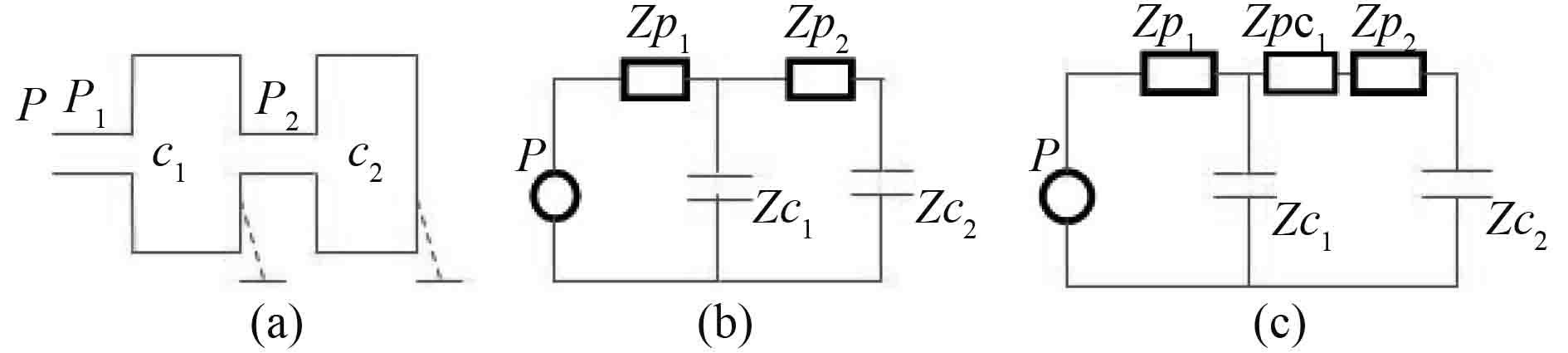
对于图 1 的复合板结构,其声学系统如图 2(a)所示。当声波穿过第 1 个短管(p1)后,一部分在充满多孔材料腔体C1 内传播消耗,终止于腔壁(“接地”)。同时另一部分穿过C1,第 2 个短管(p2),然后穿过第 2 个腔体C2,终止于刚性壁。图 2(b)图是传统声-电类比法的电路图,根据该原理,声波在短管(p1)处分支,流经短管(p2)的声波不穿过多孔材料。然本文认为,该方法有一定问题,其忽略了穿过短管(p2)的线流依然通过多孔材料,多孔材料的声阻Zpc1 对于这部分线流有消耗作用。更加合理的声-电类比图应如图 2(c)所示。
|
图 2 声电类比原理示意图 Fig. 2 Acoustic- electro analogy method schematic diagram |
结构总声阻抗为:
| $ Z = {Z_{p1}} + \frac{{\left( {{Z_{p2}} + {Z_{c2}} + {Z_{pc1}}} \right) \times {Z_{c1}}}}{{\left( {{Z_{p2}} + {Z_{c2}} + {Z_{pc1}}} \right) + {Z_{c1}}}}\text{,} $ | (12) |
由前式推导可得复合吸声材料相对声阻抗为:
| $ {Z_s} = r + jx = \frac{z}{{{\rho _0}{c_0}}}\text{,} $ | (13) |
其垂直入射时吸声系数为:
| $ \alpha = \frac{{4r}}{{{{\left( {1 + r} \right)}^2} + {x^2}}}\text{。} $ | (14) |
计算采用钢板(1.0 mm)和阻性多孔材料(流阻率为 4 800 Ns/m4),对穿孔板开孔率、空腔厚度及材料厚度影响进行分析。
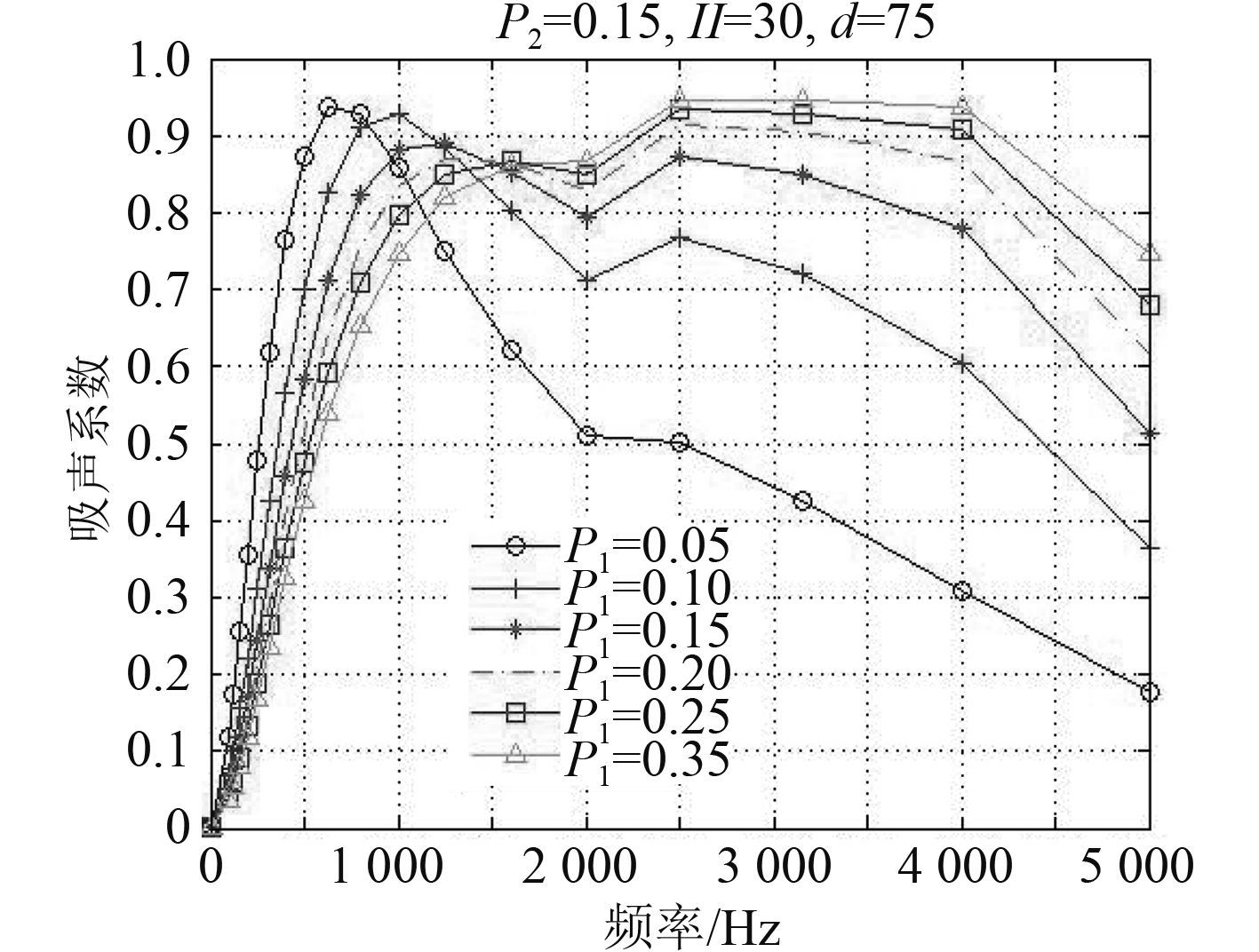
3.1 第 1 层穿孔板开孔率的影响研究取第 2 层穿孔率为 15%,多孔材料厚度为 30 mm,空腔厚度 75 mm,改变第 1 层穿孔板穿孔率大小,计算吸声系数(见图 3)。
由图 3 可得,当第 1 层板穿孔率较小时,复合吸声材料在低频有着较高的吸声系数,而在中高频阶段,吸声系数急剧下降,表明此阶段该复合材料中穿孔板组成的共振吸声结构起主要作用,而吸声材料的作用较小。因为:一层穿孔率较小时,声波进入多孔材料量较小,吸声作用没有被发挥出来,与实际情况相符。随着穿孔率逐渐增大,低频段的吸声系数逐渐减小,在中高频段,吸声系数大幅增加,而当穿孔率大于 25% 时,其吸声系数的趋于定值,此时,一般认为第 1 层穿孔板主要起支撑作用。
|
图 3 改进声电类比法 Fig. 3 Improved acoustic- electro analogy method |
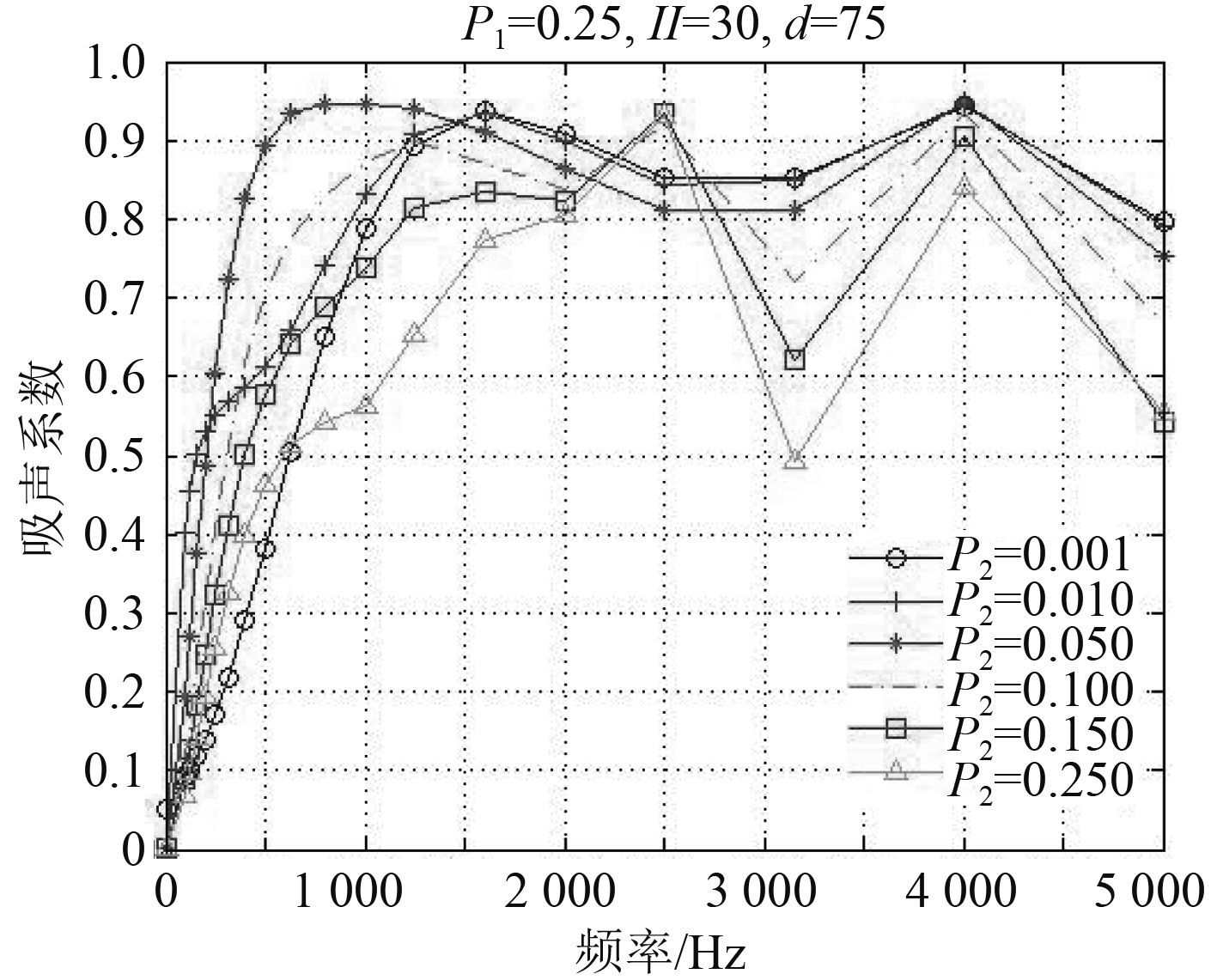
取第 1 层穿孔率为 25%,多孔材料厚度为 30 mm,空腔厚度 75 mm,改变第 2 层穿孔板穿孔率大小,计算吸声系数(见图 4 黑和图 5)。

|
图 4 改进声电类比法 Fig. 4 Improved acoustic- electro analogy method |
|
图 5 传统声电类比法 Fig. 5 Acoustic- electro analogy method |
当第 2 层穿孔板穿孔率为 0.01% 时,2 种算法的计算结果完全吻合,此种情况可以将第 2 层穿孔板看作刚性壁面,此时,该结构在中高频有着较高的吸声系数,而低频,吸声系数稍差。随着穿孔增加 2 种算法出现不同的变化规律。由改进的声-电类比法的计算结果可得,随着第 2 层穿孔板穿孔率的增大,该结构在高频段互有高低,变化不大。在 0 ~ 500 Hz 段,穿孔率为 1% 效果最好,在 500 ~ 1 000 Hz 段,穿孔率为 5% 效果较佳,之后吸声效果随着穿孔率增大而稍降低。由传统的声-电类比法计算结果可得,在高频段,当穿孔率大于 20% 时,该结构的吸声效果大幅下降,甚至远低于穿孔率为 0.1% 时的吸声效果。而由实际经验可知,当穿孔板大于 20%,即相当于透声板,多孔材料后的空腔相当于增加了材料厚度[12],其吸声效果不可能远小于无空腔时(即穿孔率为 0.01% 时)的情况。传统的声-电类比法计算结果与实际背离。传统的声-电类比法认为,多孔材料形成的等效空腔与第 2 层穿孔板及空腔形成并联,其忽视了通过第 2 层穿孔板的声波依然要通过多孔材料形成的等效空腔,多孔材料对这部分声波仍旧有吸声作用,所以该方法削弱了多孔材料的吸声作用。以上表明改进的声-电类比其合理性。
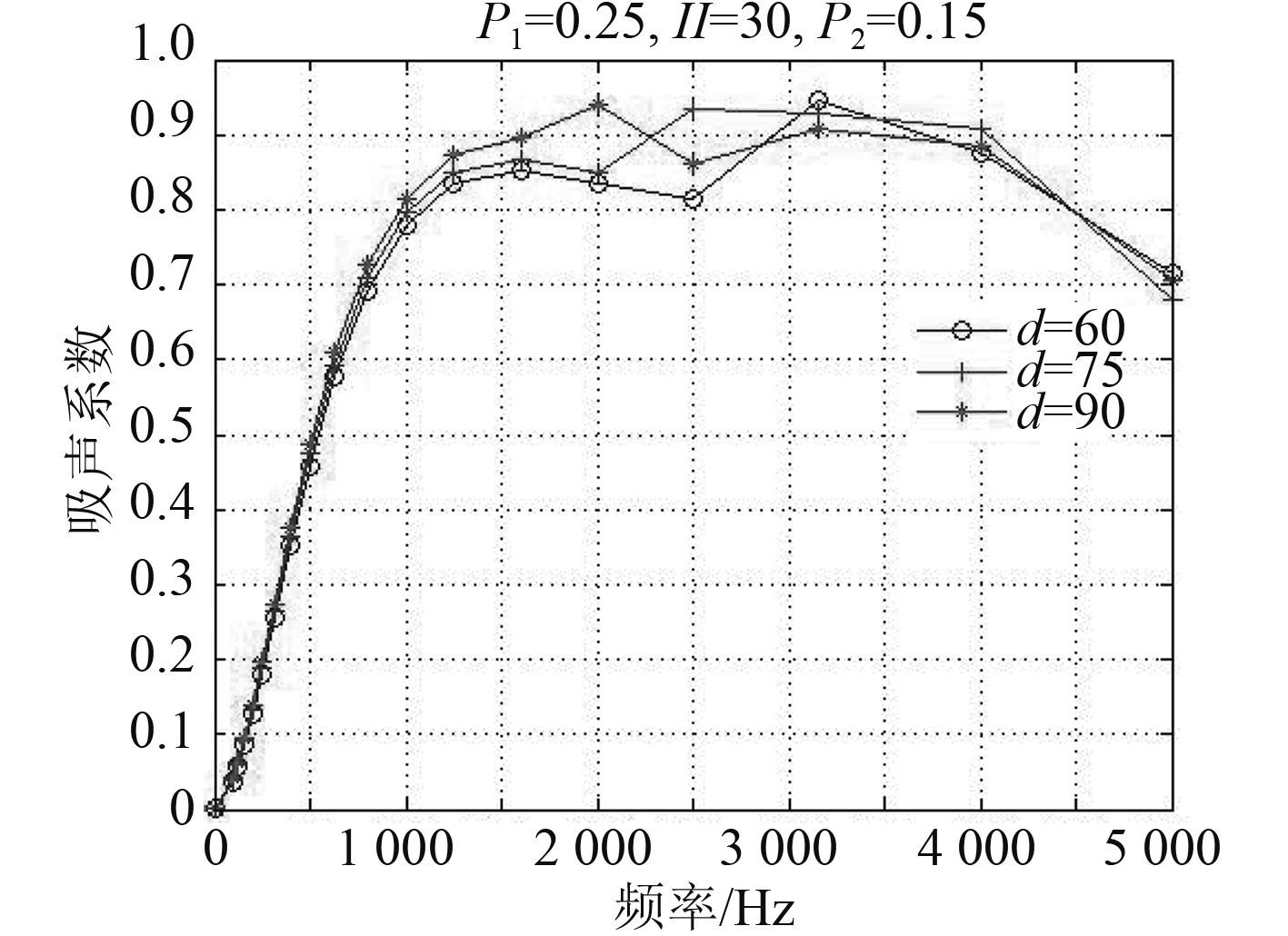
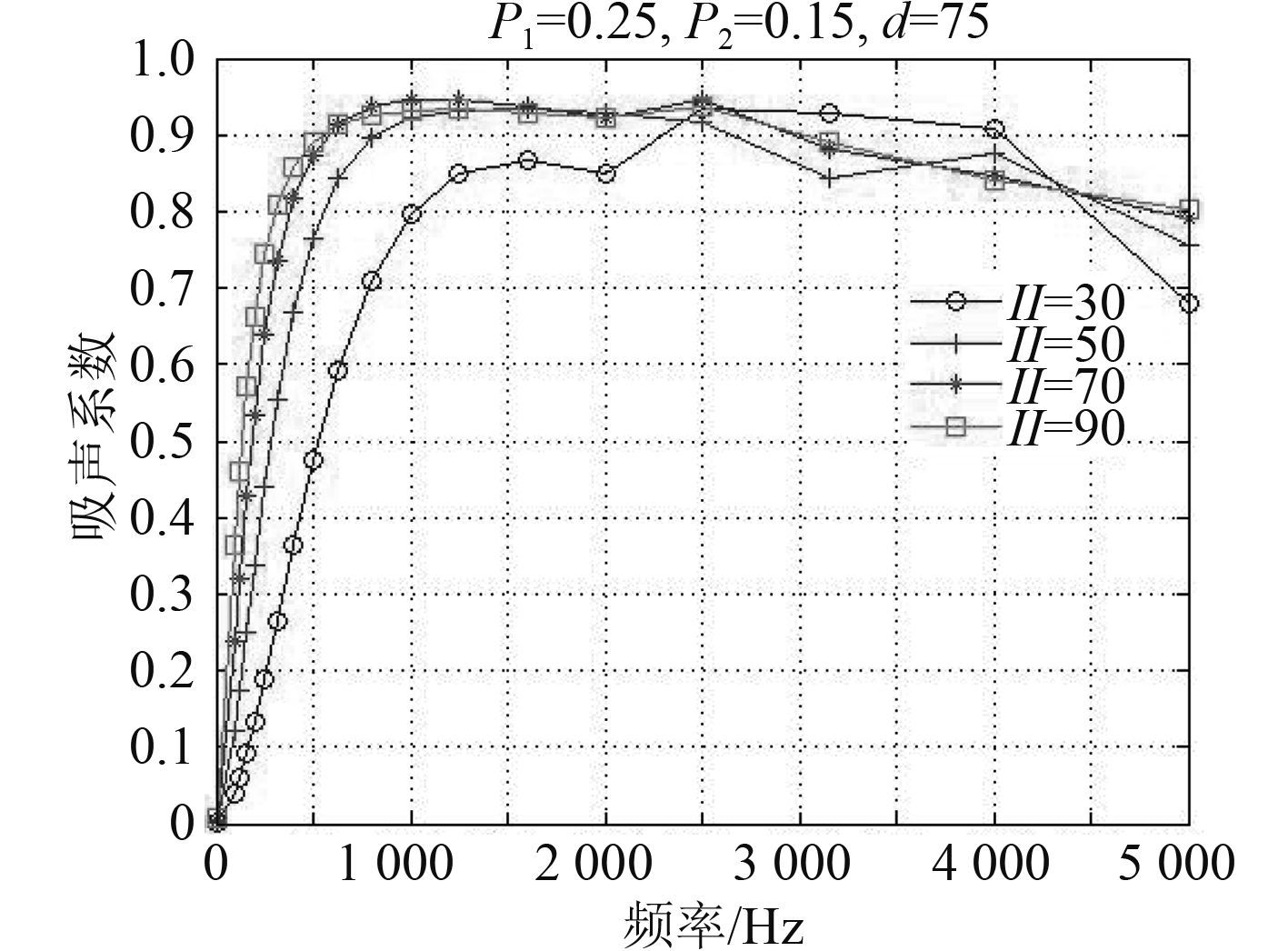
3.3 多孔材料及空腔厚度的影响研究保持第 1 层穿孔率为 25%,第 2 层穿孔率为 15%,分别改变多孔材料厚度和空腔厚度大小,计算吸声系数结果如图 6和图 7 所示。
|
图 6 空腔厚度影响图 Fig. 6 Effect of cavity thickness |
|
图 7 多孔材料厚度影响 Fig. 7 Effect of thickness of porous material |
从图 6 结果可知,吸声系数随着空腔厚度的变大而稍有增加,但影响不大,在设计时,可以与可提供空间同时考虑。图 7 则表明,增加多孔厚度会提升结构的吸声效果,然当材料厚度增大到 70 mm 以上,吸声系数增加幅度变小,趋于定值。
4 理论计算与实验本文采用实验验证所提方法的有效性,测试根据国标采用声学混响室吸声测量,在同济大学声学所混响室测试。混响室体积:268 m3,地面面积 54 m2。实验试件采用 1.0 mm 穿孔钢板(穿孔率 25%)和厚度分别为 30 mm,50 mm 的多孔材料(流阻率 4 800 Ns/m4),空腔为 75 mm,试件如图 8 所示。

|
图 8 试件与实验环境 Fig. 8 Specimen and experimental environment view |
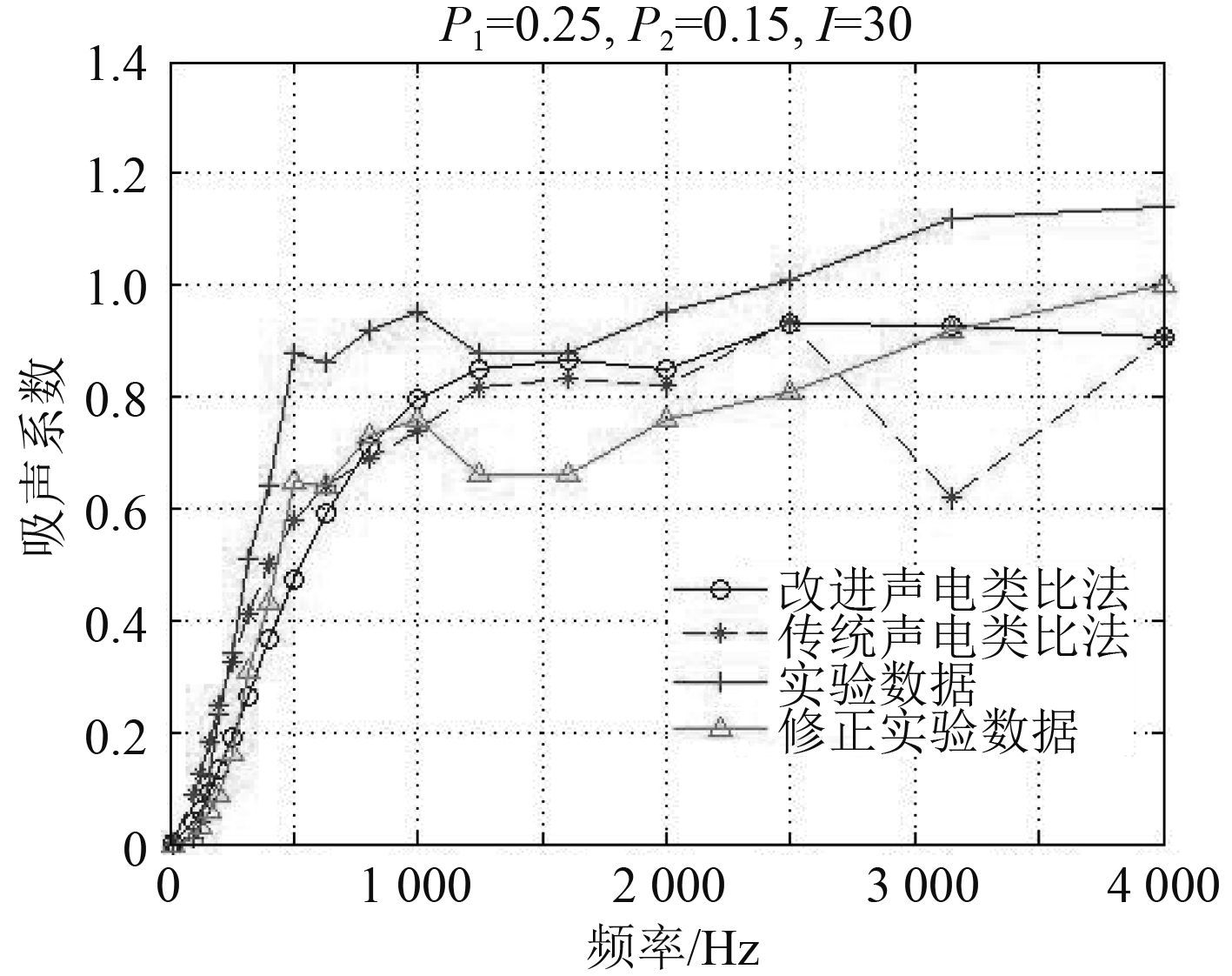
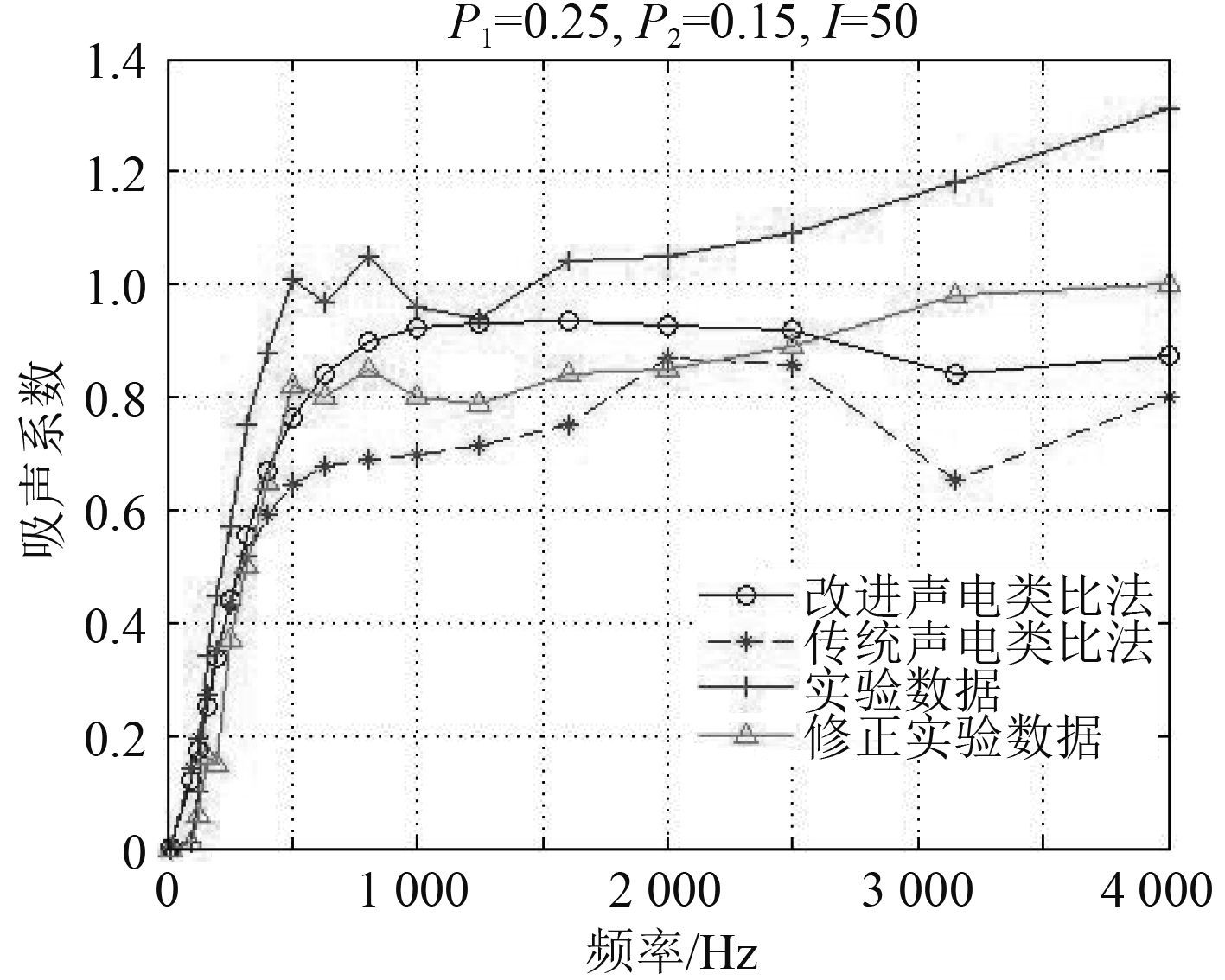
由于实验为混响测量,测定声波无规则入射时材料的吸声系数,无法保证只有材料耗能,材料的侧面,背面均有一定的吸声效果,所以会出现大于 1 的情况,这是由实验条件造成的。混响室法与驻波法结果换算可参考表 1[13],改进的声电类比法、传统声电类比法、实验结果及根据表 1 修正实验数据结果对比如图 9和图10 所示。
|
|
表 1 吸声系数换算对比表 Tab.1 Absorption coefficient conversion comparison table |
|
图 9 多孔材料厚 30 mm 时理论与实验结果对比 Fig. 9 Comparison of theoretical and experimental results of porous materials with 30 mm thickness |
|
图 10 多孔材料厚 50 mm 时理论与实验结果对比 Fig. 10 Comparison of theoretical and experimental results of porous materials with 50 mm |
根据实验结果,改进声电类比法计算结果在中低频符合很好,误差为 3.2%,而在高频误差为 9.6%。传统的声电类比法误差为 17.5%,与之相比,改进的声电类比法在中低频更加准确。而在高频,2 种算法准确度均有所下降。一是因为高频声波波长短,接近结构尺寸,穿孔板理论公式和声-电类比法计算误差大,二是另是因为实验数据按表 1 插值修正,表中αT 无大于 1 时换算值,插值计算有误差。从总体计算结果来看,与传统声电类比法相比,改进的声-电类比法更加符合实验结果,更为有效。
5 结 语本文提出的改进的声-电类比法,相较于传统的声-电类比法,考虑多孔吸声材料对流经该层,止于后层声波的吸声作用,更加全面,吸声系数计算更加精确。针对文章所研究的吸声结构,第 1 层穿孔板穿孔率、多孔材料厚度对结构吸声性能影响较大,且随频率变化。第 2 层穿孔板穿孔率及空腔厚度影响较小。在实际应用中,可据此规律,依据噪声频谱,重量限制设计最适宜的材料结构参数。该方法可指导复合材料结构参数精细化设计。
| [1] |
马大猷. 微穿孔板吸声体的准确理论和设计[J]. 声学学报, 1997, 22 (5): 385–393.
MA Da-you. General theory and design of microperforated-panel absorbers[J]. Acta Acustica, 1997, 22 (5): 385–393. |
| [2] | BERANEK L. Noise and vibration control engineering[M]. New York: John Wiley and Sorts, 1992. |
| [3] |
彭锋, 常宝军, 孙艳. 多孔吸声材料静流阻率的非线性估计[J]. 北京工业大学学报, 2012, 38 (11): 1756–1760.
PENG Feng, CHANG Bao-jun, SUN Yan. Nonlinear estimation of static flow resistivity of porous sound absor-bing materials[J]. Journal of Beijing University of Technology, 2012, 38 (11): 1756–1760. |
| [4] |
赵晓丹, 李晓, 丁瑞. 机械阻抗与声阻抗结合提高微穿孔板低频吸声性能[J]. 声学学报, 2014, 39 (3): 360–364.
ZHAO Xiao-dan, LI Xiao, DING Rui. Enhancement of low-frequency sound absorption of micro-perforated panels by adding a mechanical impedance[J]. Acta Acustica, 2014, 39 (3): 360–364. |
| [5] |
刘秀娟, 蒋伟康. 非等厚空腔微穿孔吸声结构的声学特性研究[J]. 机械科学与技术, 2010, 29 (6): 755–758.
LIU Xiu-juan, JIANG Wei-kang. Acoustic characteristics of micro-perforated panel acoustic absorbers with variable cavity depth[J]. Mechanical Science and Technology for Aerospace Engineering, 2010, 29 (6): 755–758. |
| [6] | 杜功焕. 声学基础(第三版)[M]. 南京: 南京大学出版社, 2012. |
| [7] |
朱从云, 黄其柏. 多层吸声材料吸声系数的理论计算[J]. 声学技术, 2008, 27 (1): 101–105.
ZHU Cong-yun, HUANG Qi-bai. Calculation of absorption coefficient of the multiple-layer absorbers[J]. Technical Acoustics, 2008, 27 (1): 101–105. |
| [8] |
刘新金, 刘建立, 徐伯俊, 等. 分层多孔材料吸声结构的性能分析[J]. 振动与冲击, 2012, 31 (5): 106–110.
LIU Xin-jin, LIU Jian-li, XU Bo-jun, et al. Acoustic analysis for a sound-absorbing structure with multi-layered porous material[J]. Journal of Vibration and Shock, 2012, 31 (5): 106–110. |
| [9] | P. M. 莫尔斯. K. U. 英格特, 理论声学[M]. 杨训仁译, 北京:科学出版社, 1986 |
| [10] | INGARD U. On the radiation of sound into a circular tube, with an application to resonators[J]. Acoustical Society of America, 1948, 45 (6): 665–674. |
| [11] | 徐志云. 阻抗复合吸声、消声结构的理论与声学特性研究[D]. 武汉:华中科技大学, 1999 |
| [12] | 吴九汇. 振动与噪声前沿理论及应用(第1版)[M]. 西安: 西安交通大学出版社, 2014. |
| [13] | 刘恺. 基于VA one的多孔吸声材料的应用仿真研究[D]. 武汉:武汉理工大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10497-2010164043.htm |
 2017, Vol. 39
2017, Vol. 39
