武汉第二船舶设计研究所, 湖北 武汉 430064
收稿日期: 2016-12-08.
作者简介: 张锦岚(1963-),男,研究员,研究方向为舰船总体、结构及性能设计
Analysis and optimization for sound absorption performance of porous materials based on NOVA
Wuhan Second Ship Design and Research Institute, Wuhan 430064, China
0 引 言 作为世界海洋强国重点发展的水下军事力量,潜艇具有续航能力强、作战半径大、隐蔽性好等优点,能够对陆上和海上目标实施突袭。为保证在水下完成任务而不被发现,潜艇必须尽可能降低噪声。潜艇最主要的噪声来源是机械噪声,而铺设吸声材料是降低机械噪声的重要手段之一[1]。
三聚氰胺泡沫塑料是以三聚氰胺甲醛树脂液为原料的热固型泡沫塑料,作为一种多孔材料,其具有吸声性能好、密度小、导热系数低、热稳定性高、防火性能强、安全环保以及后加工性好等一系列优点。目前,作为一种吸声材料,三聚氰胺泡沫不仅被用于建筑隔声,在飞机、舰船、汽车等交通工具中也被广泛使用[2]。
1 多孔材料声传播理论 多孔材料由固体框架部分和填充其中的流体部分组成。1956 年,Biot 提出流体饱和多孔弹性介质中的声传播理论[3-4]。该理论考虑了弹性固体框架与其内部流体之间的相对运动,并认为这种相对运动产生的摩擦导致了能量损耗。Biot 理论预测了多孔介质中 3 种波的传播,包括 2 种纵波(快波和慢波)和 1 种横波。通常认为,快波代表了液体和固体之间的同相振动,而慢波代表反相振动[5]。Biot 理论中应力-应变关系为[6],
|
$ \sigma _{ij}^s = \left[ {\left( {P - 2N} \right){\theta ^s} + Q{\theta ^f}} \right]{\delta _{ij}} + 2Ne_{ij}^s\text{,} $
|
(1) |
|
$ \sigma _{ij}^f = \left( { - \phi p} \right){\delta _{ij}} = \left( {Q{\theta ^s} + R{\theta ^f}} \right){\delta _{ij}}\text{。} $
|
(2) |
式中:
$\sigma _{ij}^s$
为框架应力张量;
$\sigma _{ij}^f$
为流体应力张量;
$e_{ij}^s$
为框架应变张量;N 为材料剪切模量;θs 和θf 分别为框架和流体的扩张量;φ 为孔隙率;p 为压力;δij 为克罗内克函数;表达如下,
|
$ \begin{array}{l} {\delta _{ij}} = 1\;\;\;\;if\;\;\;\;i = j\text{,}\\ {\delta _{ij}} = 0\;\;\;\;if\;\;\;\;i \ne j\text{。} \end{array} $
|
(3) |
P,Q,R 为弹性系数,与多孔材料的结构和属性有关。
|
$ P = \frac{{\left( {1 - \phi } \right)\left[ {1 - \phi - {K_b}/{K_s}} \right]{K_s} + \phi {K_b}{K_s}/{K_f}}}{{1 - \phi - {K_b}/{K_s} + \phi {K_s}/{K_f}}} + \frac{4}{3}N\text{,} $
|
(4) |
|
$ Q = \frac{{\left( {1 - \phi - {K_b}/{K_s}} \right)\phi {K_s}}}{{1 - \phi - {K_b}/{K_s} + \phi {K_s}/{K_f}}}\text{,} $
|
(5) |
|
$ R = \frac{{{\phi ^2}{K_s}}}{{1 - \phi - {K_b}/{K_s} + \phi {K_s}/{K_f}}}\text{。} $
|
(6) |
式中:Kb 为框架体积模量;Ks 为弹性固体体积模量;Kf 为流体体积模量。
Allard 对式(4)~ 式(6)进行了简化,对于大多数多孔介质,构成框架的材料可以认为不可压,即Ks 非常大,此时弹性系数可表示为,
|
$ P = {K_b} + \frac{{{{\left( {1 - \phi } \right)}^2}}}{\phi }{K_f} + \frac{4}{3}N\text{,} $
|
(7) |
|
$ Q = \left( {1 - \phi } \right){K_f}\text{,} $
|
(8) |
|
$ R = \phi {K_f}\text{。} $
|
(9) |
框架体积模量Kb 由下式给出,
|
$ {K_b} = \frac{{2N\left( {1 + \nu } \right)}}{{3\left( {1 - 2\nu } \right)}}\text{,} $
|
(10) |
其中ν 为框架的泊松比。
流体体积模量Kf 由下式给出:
|
$ {K_f} = {P_0}/\left( {1 - \frac{{\gamma - 1}}{{\gamma \alpha '\left( \omega \right)}}} \right)\text{,} $
|
(11) |
|
$ \gamma = {c_p}/{c_v}\text{,} $
|
(12) |
|
$ \alpha '\left( \omega \right) = \frac{{8\nu '}}{{j\omega \Lambda {'^2}}}{\left[ {1 + {{\left( {\frac{{\Lambda '}}{4}} \right)}^2}\frac{{j\omega }}{{\nu '}}} \right]^{1/2}} + 1\text{,} $
|
(13) |
|
$ \nu ' = \frac{\kappa }{{{\rho _0}{c_p}}}\text{。} $
|
(14) |
式中:P0 为环境压力;γ 为比热容比;cp 为定压比热;cv 为定容比热;ω 为频率;Λ’ 为孔隙热特征长度;κ 为流体热传导系数;ρ0 为流体密度。
2 数值计算 2.1 方法验证 NOVA 是一款由 ESI 集团推出的基于传递矩阵法(TMM)的多功能声学预报软件[7]。为验证 NOVA 计算的准确性,首先对一种多孔结构的吸声特性进行预报,并将结果与文献[6,8]中实测值进行对比。该多孔结构主要由泡沫塑料组成,其表面还覆盖着一层很薄的玻璃棉,结构背面为刚性壁,激励声源为垂直平面入射波如图 1 所示,材料参数见表 1。
表 1(Tab. 1)

表 1 多孔结构材料参数
Tab. 1 Material parameters of porous structure
| Parameters |
Plastic foam |
Glass wool |
| Thickness/mm |
38 |
0.45 |
| Porosity |
0.98 |
0.7 |
| Flow resistivity/N·s·m-4
|
5 × 103
|
1.1 × 106
|
| Tortuosity |
1.1 |
1 |
| Viscous characteristic length/μm |
151 |
9.9 |
| Thermal characteristic length/μm |
218 |
19.4 |
| Mass density of the material/kg·m-3
|
33 |
660 |
| Young’s Modulus of the material/Pa |
1.3 × 105
|
2.6 × 106
|
| Poisson’s ratio of the material |
0.1 |
0.01 |
| Structural loss factor of the material |
3.8 × 10-2
|
4.5 × 10-4
|
|
表 1 多孔结构材料参数
Tab.1 Material parameters of porous structure
|
分别计算泡沫塑料表面覆盖玻璃棉和不覆盖玻璃棉 2 种情况下结构的吸声系数,并与实测值对比(见图 2)。可以看出,NOVA 能够预报吸声系数随频率的变化趋势,并与实测值吻合较好,说明 NOVA 对多孔材料吸声性能的计算合理可靠。
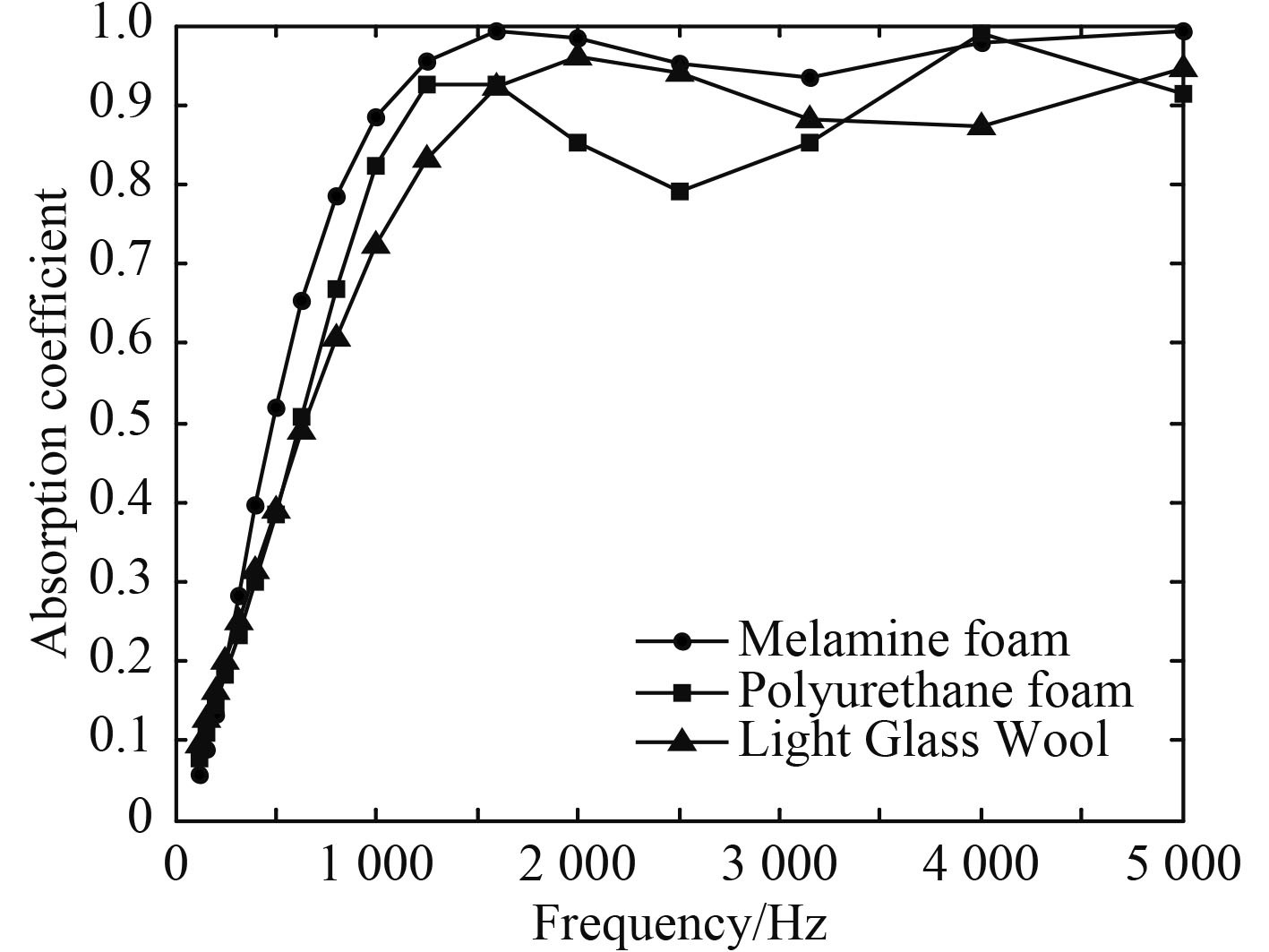
2.2 常用多孔材料吸声性能比较 图 3 是三聚氰胺泡沫、聚氨酯泡沫和玻璃棉 3 种多孔材料的吸声系数曲线。材料厚度均为 50 mm,密度分别为 8.8 kg/m3,22 kg/m3,16 kg/m3。可以看出,3 种材料均表现为低频段吸声系数较低,随着频率的升高,吸声系数逐渐增大,且增幅放缓,当频率超过某一值后,吸声系数基本不变,并出现波动。事实上,这是多孔材料吸声系数曲线的普遍趋势[9]。
从图 3 还能看出,在相同厚度下,不论是在低频区还是高频区,三聚氰胺泡沫的吸声系数普遍高于另外 2 种多孔材料,说明三聚氰胺泡沫具有良好的吸声性能。
3 正交试验 3.1 试验方案 正交试验设计是一类研究多因素水平的设计方法,可以在保证统计效果的前提下减少试验次数,提高效率。为获得具有较高吸声系数的三聚氰胺泡沫,以 NOVA 软件为基础展开正交试验,计算频率范围取 125~5 000 Hz,采用 1/3 倍频程,声源激励为垂直平面入射波,背面为刚性壁。影响因素为材料厚度、密度、孔隙率以及背面空腔厚度 4 个参数,分别记作A,B,C,D,每个因素取 4 个水平(见表 2)。不考虑因素间的相互作用,选用 L16(45)正交表[10],将 4 个因素分别放入正交表的前 4 列,第 5 列为用于统计分析的空列,共进行n = 16 组试验。
表 2(Tab. 2)

表 2 因素水平表
Tab. 2 Table of the factor leve
| Level |
Factor |
| A Density/kg·m-3
|
B Thickness/mm
|
C Porosity/%
|
D Cavity thickness/mm
|
| 1 |
5.2 |
20 |
90 |
0 |
| 2 |
7.4 |
45 |
93 |
30 |
| 3 |
8.8 |
70 |
96 |
60 |
| 4 |
10.4 |
95 |
99 |
100 |
|
表 2 因素水平表
Tab.2 Table of the factor leve
|
正交试验的方案及结果见表 3,由于不同频率下材料的吸声系数不同,以各中心频率吸声系数的算术平均值作为材料吸声性能的评价指标。
表 3(Tab. 3)

表 3 试验方案及结果
Tab. 3 Experimental scheme and results
| Number |
Factor |
Average absorption coefficient |
| A
|
B
|
C
|
D
|
Error
|
| 1 |
5.2 |
20 |
90 |
0 |
|
0.325 6 |
| 2 |
5.2 |
45 |
93 |
30 |
|
0.704 2 |
| 3 |
5.2 |
70 |
96 |
60 |
|
0.848 9 |
| 4 |
5.2 |
95 |
99 |
100 |
|
0.896 4 |
| 5 |
7.4 |
20 |
93 |
60 |
|
0.552 8 |
| 6 |
7.4 |
45 |
90 |
100 |
|
0.818 4 |
| 7 |
7.4 |
70 |
99 |
0 |
|
0.741 1 |
| 8 |
7.4 |
95 |
96 |
30 |
|
0.857 3 |
| 9 |
8.8 |
20 |
96 |
100 |
|
0.614 4 |
| 10 |
8.8 |
45 |
99 |
60 |
|
0.774 5 |
| 11 |
8.8 |
70 |
90 |
30 |
|
0.800 1 |
| 12 |
8.8 |
95 |
93 |
0 |
|
0.812 0 |
| 13 |
10.4 |
20 |
99 |
30 |
|
0.485 3 |
| 14 |
10.4 |
45 |
96 |
0 |
|
0.593 9 |
| 15 |
10.4 |
70 |
93 |
100 |
|
0.877 2 |
| 16 |
10.4 |
95 |
90 |
60 |
|
0.873 5 |
| Kj1
|
2.775 1 |
1.978 1 |
2.817 6 |
2.472 6 |
2.834 6 |
|
| Kj2
|
2.969 6 |
2.891 0 |
2.946 2 |
2.846 9 |
2.933 2 |
K = 11.575 6
|
| Kj3
|
3.001 0 |
3.267 3 |
2.914 5 |
3.049 7 |
2.964 6 |
P = 8.374 7
|
| Kj4
|
2.829 9 |
3.439 2 |
2.897 3 |
3.206 4 |
2.843 2 |
Q = 8.783 2
|
| Qj
|
8.383 5 |
8.693 5 |
8.376 9 |
8.450 1 |
8.377 8 |
|
| Sj2
|
0.008 9 |
0.318 9 |
0.002 2 |
0.075 4 |
0.003 2 |
ST2 = 0.408 5
|
|
表 3 试验方案及结果
Tab.3 Experimental scheme and results
|
3.2 数据分析 为探究 4 个因素对材料吸声性能的影响程度,对试验数据进行统计学分析[11]。将试验结果即平均吸声系数记为yi(i = 1,2,…,n),设每个因素取r 种水平,全部试验中包含某一水平的方案有m 个。对于本文所采用的试验方案,r = 4,m = 4。令Kjl 为第j 列(包括空列)中水平l(l = 1,2,…,r)所对应的全部试验结果之和,即
|
$ \left\{ \begin{array}{l} {K_{11}} = {y_1} + {y_2} + {y_3} + {y_4}\text{,}\\ {K_{12}} = {y_5} + {y_6} + {y_7} + {y_8}\text{,}\\ \;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \end{array} \right. $
|
(15) |
表 3 中其他统计量按下式计算,
|
$ K = \sum\limits_{l = 1}^r {{K_{jl}}} = \sum\limits_{i = 1}^n {{y_i}}\text{,} $
|
(16) |
|
$ Q = \sum\limits_{i = 1}^n {y_i^2} \text{,} $
|
(17) |
|
$ P = \frac{1}{n}{K^2}\text{,} $
|
(18) |
|
$ {Q_j} = \frac{1}{m}\sum\limits_{l = 1}^r {K_{_{jl}}^2} \text{,} $
|
(19) |
|
$ S_j^2 = {Q_j} - P\text{。} $
|
(20) |
|
$ S_T^2 = Q - P\text{,} $
|
(21) |
基于上述统计量,对正交试验数据进行方差分析(见表 4),取显著性水平α = 0.05。计算各因素所对应的p 值,并进行比较。
表 4(Tab. 4)

表 4 方差分析
Tab. 4 The analysis of variance
| Factor |
Quadratic Sum |
DOF |
Mean Square Deviation |
F
|
p
|
| A
|
0.008 9 |
3 |
0.003 0 |
2.803 7 |
0.209 8 |
| B
|
0.318 9 |
3 |
0.106 3 |
100.988 3 |
0.001 6 |
| C
|
0.002 2 |
3 |
0.000 7 |
0.712 0 |
0.606 6 |
| D
|
0.075 4 |
3 |
0.025 1 |
23.882 3 |
0.013 5 |
| Error
|
0.003 2 |
3 |
0.001 1 |
|
|
| Total |
0.408 5 |
15 |
|
|
|
|
表 4 方差分析
Tab.4 The analysis of variance
|
|
$ {p_B} < {p_D} < \alpha < {p_A} < {p_C}\text{。} $
|
(22) |
上述结果说明B 材料厚度(20~95 mm 范围内)和D 背面空腔厚度(0~100 mm 范围内)对材料吸声性能存在显著性影响,且材料厚度的影响更显著。而A 材料密度(5.2~10.4 kg/m3 范围内)和C 孔隙率(90%~99% 范围内)对材料吸声性能无显著性影响。
对于B 因素和D 因素,从表 3 中可看出,
|
$ \begin{array}{l} {K_{21}} < {K_{22}} < {K_{23}} < {K_{24}}\text{,}\\ {K_{41}} < {K_{42}} < {K_{43}} < {K_{44}}\text{。} \end{array} $
|
(23) |
所以 2 个因素中较优的水平分别是B4 和D4,即材料和背面空腔的厚度越大,吸声性能越好。对于A 因素和C 因素,因为影响不显著,从降低成本和便于运输的角度考虑,可选择密度较小、孔隙率较高的材料。因此,本次正交试验确定的较优的因素水平组合为A1B4C4D4,即材料密度为 5.2 kg/m3,厚度为 95 mm,孔隙率为 99%,背面空腔厚度为 100 mm。这一组合恰好是试验方案中的第 4 组,而该组方案的平均吸声系数为 0.869 4,是 16 组试验方案中结果最好的。
4 结 语 1)利用 NOVA 软件对多孔材料进行声学预报,发现三聚氰胺泡沫的吸声性能明显优于等厚度的玻璃棉和聚氨酯泡沫。
2)利用正交试验,找到使三聚氰胺泡沫吸声性能最佳且最合适的因素水平组合,即材料密度为 5.2 kg/m3,厚度为 95 mm,孔隙率为 99%,背面空腔厚度为 100 mm。
3)通过方差分析发现,材料厚度和背面空腔厚度对三聚氰胺泡沫的吸声性能有显著影响,材料密度和孔隙率则没有显著影响。


 2017, Vol. 39
2017, Vol. 39
