复合材料结构由于具有良好的力学性能,已越来越多应用于舰船结构[1-2]。舰船的上层建筑在建造中有着较高要求,其外壳可以采用复合材料代替传统钢结构。上层建筑采用分段建造吊装,可提高劳动生产效率、缩短建造周期、降低建造成本,但是复合材料上层建筑结构具有复合材料板格尺度大、刚度小的特点,使得其相较于传统的钢结构舱段,有更高的吊装工艺要求。吊装前需要对分段添加的各类加强结构,这一方面会增加整个工程施工成本,另一方面对结构进行加强的焊接等工艺不可避免的会影响原始结构的力学特性[3]。如何保证分段在吊装过程中的强度和变形要求,合理的设计起吊方案以及加强方案成为吊装中的实际问题。
ZHANG J P 等[4]对大型船舶分段吊装方案进行研究,提出船舶分段吊装的工艺要求和注意事项。杨永谦等[5] 计算了上层建筑结构在吊装过程中的变形和应力状态,并与实测值进行了比较,为上层建筑进行整体吊装的可行性提供了依据。钟兴锦[3] 运用有限元分析软件建立船舶分段模型,进行强度分析,将有限元分析结果和理论计算结果进行比较,制定出规范的分段吊装计算方法。张延昌等[6] 利用有限元软件对油船上层建筑结构在自重作用下的响应进行了分析,提出合理有效的结构加强措施。李永正等[7] 以某大型 FPSO 为研究对象,利用有限元软件对其上层建筑整体吊装进行有限元强度分析。但是关于以复合材料为主体的复合材料上层建筑分段吊装研究目前相对较少。
本文结合船舶的某一典型分段,通过有限元方法,分析复合材料上层建筑在吊装过程中的强度与刚度特性,确保上层建筑分段在吊装过程中,不发生较大的变形乃至破坏等问题;结合工程实际,给出合理的局部加强方案和最优的吊装方案。
1 复合材料板上层建筑模型 1.1 复合材料上层建筑建模复合材料上层建筑在建造过程中,首先在内场进行分段建造,然后分段吊装上船台,本文以某一典型分段(见图 1)为例介绍其结构特点。分段结构是由复合材料壳板和钢制骨架组合而成,按设计要求焊接好钢骨架后,将预制好的复合材料板格铺设于钢骨架之上,并与钢结构梁通过螺栓进行连接。铺设的复合材料板为 3 层夹芯板结构,外部 2 层为层合板,中间层为 PVC 泡沫材料。
|
图 1 上层建筑示意图 Fig. 1 Schematic diagram of superstructure |
由于本文主要考虑在吊装过程中分段的变形控制和应力控制,而螺栓本身的刚度很大,对于整个分段吊装力学性能而言,螺栓的影响较小。同时,由于实际分段中壳板安装在钢骨架上所用的螺栓的数量很多,且螺栓与骨架连接部位都存在复杂的接触关系,因此有必要对实际模型进行简化。在有限元模型中,并不直接建立螺栓结构,但考虑其质量,将其质量分摊到支撑复合材料壳板的钢骨架上。同时考虑到焊接[8] 等工艺因素,对钢骨架密度进行调整,保证分段质量合理准确。
简化后的有限元模型中钢骨架采用梁单元,复合材料壳板采用复合材料板单元。单元长度划分为 30 mm,并通过试算检验了网格大小的合理性,有限元模型如图 2 所示。

|
图 2 上层建筑有限元模型 Fig. 2 The FEM model of superstructure |
不同的起吊方式对上层建筑吊装过程中的力学特性影响不同,为了在有限元仿真计算中选择较为合理的起吊约束方式,需选择不同的起吊约束方案进行对比计算(有限元模型中约束点的位置即为初选的起吊点)。由于复合材料板是以螺栓连接的方式安装在钢骨架上,考虑到需要在分段上焊接起吊工装,起吊点只能选择在钢骨架上。对不同的起吊约束模型方案进行对比计算,从中选取偏于保守的方案作为有限元模型计算的约束方案。
首先初步设定起吊点在纵横钢骨架的 4 个交点上,如图 3 所示。图 3 和图 4 分别给出了 2 种起吊约束方案。图 3 中,在高于分段平面 5 m 处设置“固定”的假设吊钩点,将分段上的 4 个起吊点和吊钩所在的节点进行x、y 和z 三个方向的平动耦合约束(约束方案 1);图 4 中,对分段的 4 个吊装点,仅约束竖直方向上的位移(约束方案 2),相当于吊钩点位于分段正上方的无穷远处。
|
图 3 上层建筑分段吊装点平动耦合约束 Fig. 3 The translational coupling constraints of superstructure subsection hoisting point |

|
图 4 上层建筑分段吊装点的竖直约束 Fig. 4 The vertical constraints of block hoisting point |
在起吊计算中,根据船舶上层建筑吊装规范[9],考虑起吊加速度带来的惯性载荷影响,取垂向重力加速度为 1.1g(g 为重力加速度),其余方向为 0。由于起吊作业过程比较缓慢,因此可以认为是一个准静态的过程,对模型进行静力分析,并选取 Mises 应力和合成位移作为应力和变形的参考值。
对于复合材料板组成的上层建筑,吊装中主要考虑钢骨架以及复合材料壳板的变形。若复合材料板吊装时变形过大,有可能不利于后续安装,甚至对复合材料板产生破坏。因此分段吊装的主要参考指标为板格的变形,工程要求变形小于 6 mm,同时兼顾结构的应力水平。
上层建筑分段在 2 种约束方案下分别进行了静力计算,其计算应力与位移结果如图 5 和图 6 所示。
|
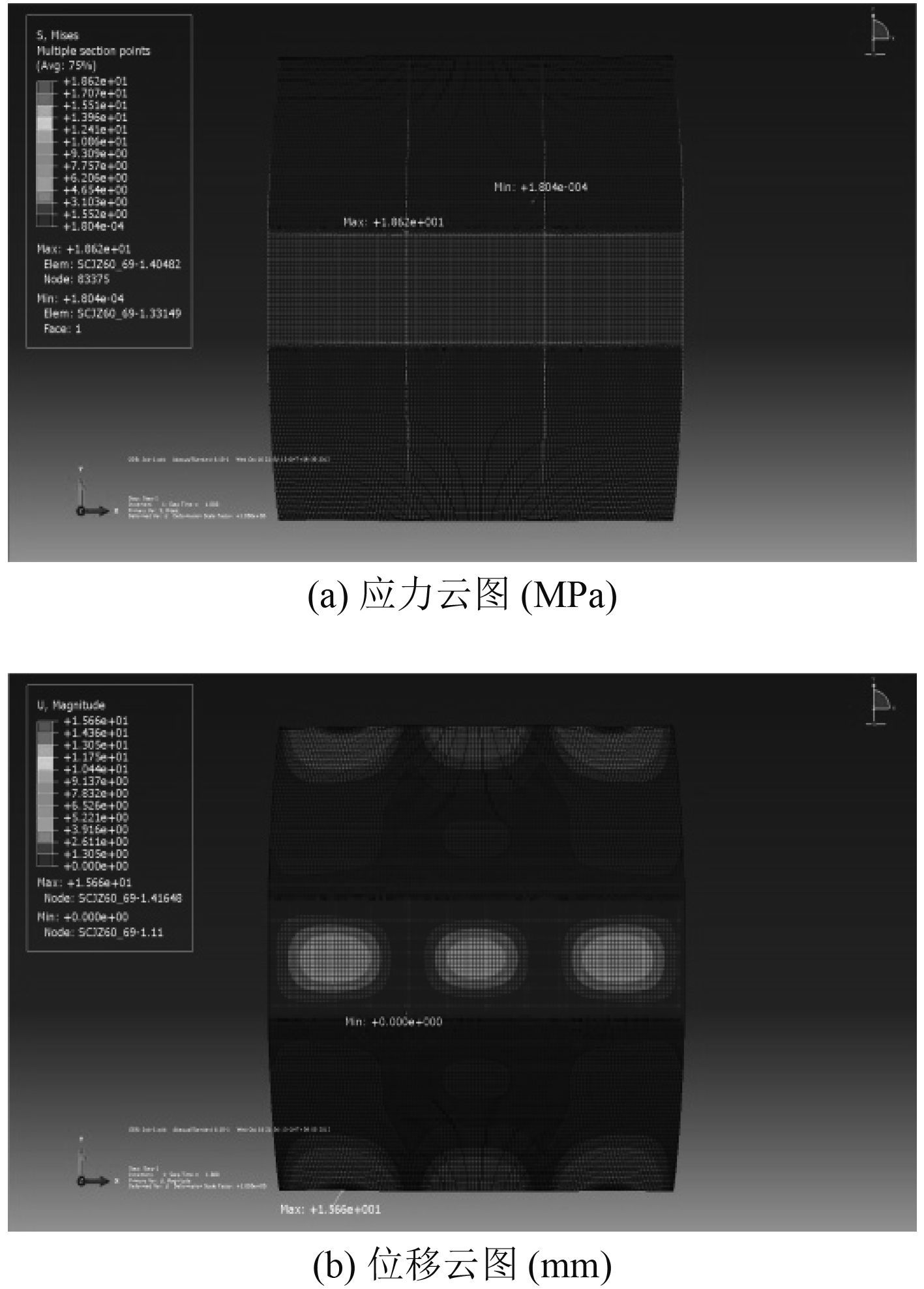
图 5 上层建筑分段采用约束方案 1 的应力和位移云图 Fig. 5 The Mises stress and Magnitude displacement nephogram of hoisting plan 1 |

|
图 6 上层建筑分段采用约束方案 2 的应力和位移云图 Fig. 6 The Mises stress and Magnitude displacement nephogram of hoisting plan 2 |
由图 5 和图 6 结果对比可知:对于起吊点竖直约束(方案 2)的情况,最大合成位移为 17 mm,位置在边界的板格自由边上;而方案 1 的耦合约束方案中板格最大合成位移 15 mm,可见方案 2 竖直起吊约束会使计算结果偏大。和方案 2 中的竖直约束相比,因为约束方案 1 会使得吊索产生较大的横向力,该力会抑制板格的变形。因此,应选取偏于保守结果的约束方案,即在分段的吊点上都采用施加竖直方向的约束作为边界条件。
1.3 加强方案的确定从 1.2 节分析可知,分段的壳板结构依然有 17 mm 的静变形,与工艺要求的最大变形控制在 6 mm 以内相差甚远,故有必要对分段进行局部加强。由图 5 和图 6 位移云图可知分段的最大位移均发生在自由边界,综合考虑实际中的吊装工艺,有必要在分段结构的自由边上进行加强,加强方案如图 7 所示(图中粗黑线标出)。考虑到实际工艺,选取 16 a 槽钢加强,其加强后的效果如图 8 所示。

|
图 7 上层建筑分段的加强方案 Fig. 7 The reinforce plan of superstructure subsection |

|
图 8 上层建筑分段加强后效果图 Fig. 8 The figure of superstructure subsection after strengthened |
根据前文选择的加强和起吊方式,需要选择合理的起吊点位置,确保起吊过程中分段的应力和变形都比较小,从而确定起吊方案。考虑工艺易于实现,选取的起吊点位置主要分布在上层建筑的钢骨架相交处以及结构的水平方向的钢骨架上。提出 4 种吊装方案:方案 1 起吊点位于中间骨材交点处,方案 2 起吊点位于边界骨材交点处,方案 3 起吊点位于中间骨材与边界骨材中点处(1/2 位置),方案 4 起吊点位于中间骨材与边界骨材靠近中间 1/4 位置处,各方案如图 9 所示。

|
图 9 上层建筑分段吊装方案 Fig. 9 The hoisting plan of superstructure subsection |
为防止分段在吊装过程中发生侧翻,要求分段重心落在 4 个吊点组成的平面的竖直投影范围内。经计算,以上提出的各方案均满足此要求。
由表 1 及图 10 应力和变形云图可知,上层建筑分段在不同的吊装方案中,吊装应力均远小于钢结构的屈服应力。比较 4 种吊装方案,方案 3 和方案 4 均为较优结果,应力变形条件均满足吊装工艺要求,方案 3 最大变形位于中部水平板上,方案 4 最大变形位于两侧水平板,考虑到在实际吊装过程中,由于绳索与板面存在夹角,故会在一定程度上会减小板两侧的变形,而会加大板中部的变形,故在实际吊装过程中,方案 4 较方案 3 更优。
|
|
表 1 上层建筑分段吊装计算结果 Tab.1 Summary of structure stress and deformation calculation results caused by lifting |

|
图 10 上层建筑分段四种吊装方案下的应力云图及变形云图 Fig. 10 The Mises stress and Magnitude displacement nephogram of superstructure subsection for four hoisting plans |
上节主要计算了上层建筑分段整体在吊装过程中的板格变形,并通过计算结果讨论,给出了上层建筑分段的预选起吊方案。然而,由于对模型螺栓连接进行的简化处理使得有限元仿真模型的刚度增大,因此本节考虑将模型中的复合材料板移除,但将其质量通过调整钢骨架密度的方式分摊到上层建筑的钢骨架上。这样,在保持模型总质量不变的情况下,移除了复合壳板部分的刚度,使得整个分段的刚度仅由钢骨架来承担,故计算出的结果偏于保守和安全。以此来考察钢骨架在吊装过程中是否会产生过大的变形。如图 11 所示,为上层建筑分段的全钢骨架有限元模型,通过改变钢骨架的密度,将复合材料壳板及螺栓的质量分摊到钢骨架上。

|
图 11 上层建筑分段全钢骨架模型 Fig. 11 The steel skeleton model of block |
|
|
表 2 上层建筑分段骨架计算结果 Tab.2 Summary of structure stress and deformation calculation results caused by lifting |
由表 2 及图 12 应力变形云图可知,对于钢骨架结构,吊装过程中的应力远小于钢结构的屈服应力。比较 4 种吊装方案,方案 3 和方案 4 均为较优结果,这与整体吊装计算的结果一致;同样,方案 3 最大变形位于骨材上下边中部,方案 4 最大变形位于骨材上下边四角。在实际吊装过程中,由于起吊的绳索与板面存在角度,故会在一定程度上减小板两侧的变形。同时考虑到上节整体计算中板格的变形,可以确定上层建筑分段吊装方案 4 为最优方案。从以上计算结果中可见,在偏于保守的计算中,提出的方案满足工艺要求,进一步说明了加强方案和起吊方案的合理性。

|
图 12 上层建筑分段骨架 4 种吊装方案下的应力云图及变形云图 Fig. 12 The Mises stress and Magnitude displacement nephogram of steel skeleton models for four hoisting plans |
上层建筑复合材料板与钢骨架是以螺栓连接,因此有必要校核上层建筑吊装过程中螺栓的强度。通过静力计算的结果提取 4 个吊点的支反力,取吊绳和分段平面的夹角为 60°,则可以得到垂向力和切向力,由于每个吊点位置布置有 4 个螺栓,选取危险的情况,假设 4 个中只有 2 个受力,计算出每个螺栓所受的拉应力、切应力和挤压应力分别为 22.814 MPa,13.171 MPa 和 7.898 MPa。
上层建筑采用的螺栓为 8.8 级螺栓,查询规范取安全系数为 3,根据机械设计手册可得螺栓的许用切应力为
本文结合舰船典型复合材料分段的吊装工艺,通过有限元方法,分析了复合材料上层建筑分段吊装过程中的力学特性,选择了较为合理的加强方案和吊装方案,结合工程实际给出了优选的吊装方案并得到如下结论:
1)对上层建筑吊装过程而言,自由边会产生较大的变形,因此需要对自由边进行加强,经计算 16 a 槽钢满足要求。
2)针对上层建筑分段,提出了 4 个吊装方案,对比分析应力和变形并考虑最大变形位置,选择了方案 4,为工程实际吊装提供参考。
3)将复合材料板和螺栓结构均简化到钢骨架上,进行偏危险的吊装方案计算,为实际吊装提供进一步参考。实际施工过程中采用本文给出的吊装方案,顺利完成了分段吊装任务。
| [1] | SMITH M C. Design of marine structures in composite materials[J]. Theoretical &Applied Mechanics, 1990, 6 (1): 293–310. |
| [2] | HE Kai. Numerical analysis for hull strength and delamination damage of composite marine structures[M]. Shanghai: Shanghai Jiao Tong University, 2012. |
| [3] |
钟兴锦. 船舶分段吊装的计算及其有限元分析[D]. 大连:大连理工大学, 2013.
ZHONG Xing-jin. The calculation and finite element analysis of ship block's lifting[D]. Dalian:Dalian University of Technology, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10141-1013201545.htm |
| [4] | ZHANG J P, TU L H. Research on combined lifting conceptual design for large-scale ship[J]. Advanced Materials Research, 2011, 295 : 473–476. |
| [5] |
杨永谦, 黄贻平, 陈超核. 29000 t货船上层建筑整体吊装变形及应力计算[J]. 武汉交通科技大学学报, 1994, 03 : 301–306.
YANG Yong-qian, HUANG Yi-ping, CHEN Chao-he. Calculation of deformation and stresses of 29000 t cargo ship's superstructure in integral assembly[J]. Journal of Wuhan Transportation University, 1994, 03 : 301–306. |
| [6] |
张延昌, 王自力, 罗广恩. 船舶上层建筑整体吊装强度有限元分析[J]. 船舶工程, 2006 (3): 62–65.
ZHANG Yan-chang, WANG Zi-li, LUO Guang-en. FE analysis of the complete lifting and mounting strength of ship superstructure[J]. Ship Engineering, 2006 (3): 62–65. |
| [7] |
李永正, 曹轶, 窦培林, 等. 基于FPSO上层建筑不同吊装方案的变形控制研究[J]. 舰船科学技术, 2015 (1): 29–33.
LI Yong-zheng, CAO Yi, DOU Pei-lin. Research on numerical simulation of superstructure integral hoisting of FPSO[J]. Ship Science and Technology, 2015 (1): 29–33. |
| [8] |
李鹏, 杨亮, 冯朝闻, 等. 船舶焊接重量控制的研究与应用[J]. 金属加工(热加工), 2015 (10): 45–48.
LI Peng, YANG Liang, FENG Zhao-wen, et al. The research and application of weight control of ship welding[J]. Metal Processing (thermal processing), 2015 (10): 45–48. |
| [9] |
中国船级社.船体结构强度直接计算[S].北京:人民交通出版社, 2001.
CCS. Direct calculation of hull structural strength[S]. Beijing:China Communications Press, 2001. |
 2017, Vol. 39
2017, Vol. 39
