2. 上海交通大学 船舶与海洋工程国家重点实验室, 上海 200240
2. State Key Laboratory of Ocean Engineering, Shanghai Jiaotong University, Shanghai 200240, China
五体船是一种由一个经过水动力优化处理的细长型主体与前后两侧配备的 4 个提供稳性的片体组成的多体船[1-2],五体船以其在耐波性、适航性、阻力性能及节能减排方面的优秀表现已引起国内外学者的关注[3-5]。但在空载或小摇荡时由于 2 个前片体在水面之上,则五体船各性能与三体船无异[6],致使空载耐波性削弱。1981 年美国华盛顿大学的 Calkins 首次提出多体水翼船的概念[7-8],多体水翼船是水翼船与多体船的融合船型,兼具多体船和水翼船的优点,目前国内外学者主要集中在双体水翼船方面的研究。
本文基于以上两点,针对水翼五体船进行耐波性优化分析。水翼五体船是以五体船为依托,通过在主船体及片体之间加装水翼构造而得的复合型五体船,静浮时前水翼横向倾斜半出水,后水翼横向水平下潜水中。本文借助耐波性通用软件 HydroSTAR 计算在波浪中的纵摇、垂荡、横摇等运动,研究加装不同攻角水翼对五体船耐波性改善情况。
1 耐波性计算方程 1.1 纵摇、垂荡耦合运动方程船舶在波浪作用下,沿z 轴的往复运动为垂荡,绕y 轴的往复转动便是纵摇。垂荡的运动情况可以用纵向位移z、纵向位移速度
根据切片法思想,某处垂向相对位置:
| $ {z_R} = z - X\theta - {\rm{\zeta }}\text{,} $ |
式中:X 为纵向位置;θ 为纵摇角。
等效波面方程为:
| $ {\zeta ^*} = {e^{ - k{T_m}}}{{\rm{\zeta }}_A}\cos \left( {kx\cos \beta - ky\sin \beta + {\omega _e}t} \right)\text{,} $ |
则可得切片所受流体动力如下:
流体静力
| $ F{'_1} = - 2{\rm{\rho}} gb\left( {{\rm{z}} - {\rm{X\theta }} - {{\rm{\zeta }}^*}} \right)\text{,} $ |
兴波阻力
| $ F{'_2} = - {N_H}\left( {\dot z - X\dot \theta + V\theta - {{{\rm{\dot \zeta }}}^{\rm{*}}}} \right)\text{,} $ |
附加惯性力
| $ F{'_3} = - {M_H}\left( {\ddot z - X\ddot \theta + 2V\dot \theta - {{{\rm{\ddot \zeta }}}^*}} \right) + V\frac{{{\rm d}{M_H}}}{{{\rm d}X}}(\dot z - X\dot \theta + V\theta - {{\rm{\ddot \zeta }}^*})\text{,} $ |
式中:NH 为阻尼系数;MH 为附加质量;V 为船速。
沿船长积分可得垂荡力及纵摇力矩:
| $ \begin{array}{l} {F_Z} = \int\limits_L {(F{'_1} + F{'_2} + F{'_3}){\rm d}X}\text{,} \\ {M_\theta } = \int\limits_L {X(F{'_1} + F{'_2} + F{'_3}){\rm d}X} \text{。} \end{array} $ |
根据牛顿第二定律可得船体垂荡和纵摇运动方程:
| $ \begin{array}{l} \displaystyle\frac{D}{{\rm{g}}}z = {F_z}\text{,}\\ {I_{YY}}\ddot \theta = {M_\theta }\text{。} \end{array} $ |
式中:D 为排水量;IYY 为纵向惯性矩。
1.2 横摇运动方程在波浪作用下,船体会绕x 轴往复转动,这种转动便是横摇。横摇的运动情况可以用横摇角度φ、横摇角速度
| $ - {I'_{xx}}\ddot \varphi - 2N\dot \varphi - Dh\varphi + Dh{a_m} = 0\text{,} $ |
式中:I’xx 为总惯性矩;φ 为横摇角;am 为有效波倾角;D 为排水量;N 为横摇阻尼力矩系数;h 为初稳性高。
由
| $ {I'_{xx}}\ddot \varphi + 2N\dot \varphi + Dh\varphi = Dh{a_{{m_0}}}\sin \omega t\text{。} $ |
将上式各项均除以I’xx,并引入新符号:
| $ \begin{array}{l} 2\upsilon = \displaystyle\frac{{2N}}{{{{I'}_{xx}}}}\text{,}\\[8pt] \omega _\varphi ^2 = \displaystyle\frac{{Dh}}{{{{I'}_{xx}}}}\text{,} \end{array} $ |
可得横摇运动方程:
| $ \ddot \varphi + 2\upsilon \dot \varphi + \omega _\varphi ^2\varphi = {a_{{m_0}}}\omega _\varphi ^2\sin \omega t \text{。}$ |
本文采用挪威船级社 BV 的 HydroSTAR 水动力分析软件进行垂荡、纵摇、横摇的分析计算。HydroSTAR 软件基于三维势流理论,能够在有限水深或无限水深的环境条件下对单个或多个船体及海洋结构物的波浪载荷及波浪诱导运动进行完整的求解。通过将 HydroSTAR 计算所得 Wigley 单体船的垂荡及纵摇响应幅值算子与 Wigley 船体模型试验结果对比,发现 HydroSTAR 的计算结果与试验值相吻合[9],用 HydroSTAR 软件对耐波性进行分析计算比较可靠。
2.2 模型参数本文研究重点为加装不同攻角水翼对五体船耐波性的改善情况,主船体及片体采用 Wigley 船型,水翼采用 NACA 四位数字标准翼型。Wigley 船型是国际上通用的一种数学船型,船型瘦长,符合线性理论小扰动假定[10],NACA 四位数字翼型是美国 NACA 最早建立的一个低速翼型系列,有较高的最大升力系数和较低的阻力系数,适合用于快速艇水翼[11]。船型参数及翼型参数见表 1和表 2。
|
|
表 1 船型参数 Tab.1 Parameter of pentamaran |
|
|
表 2 翼型参数 Tab.2 Parameter of hydrofoil |
五体船的侧体布局优化基本朝同一趋势发展,前侧体纵向位置基本稳定在主船体船中附近,后侧体纵向位置则主要集中于主船体尾部,若假定前后侧体的横向坐标一致,则其大致分布于距船中纵剖面 1.5 倍半船宽位置[9]。本文据此将前侧体置于主船体船中稍前位置,后侧体置于船尾,前后侧体横向位置一致,位于 1.5 倍船宽处。水翼均置于侧体中间部分,用于连接 4 个侧体和主船体。后水翼横向水平,前水翼从前侧体向下斜插入水中。具体船型如图 1和图 2 所示。

|
图 1 水翼五体船 Fig. 1 Hydrofoil-pentamaran |
|
图 2 水翼五体船(主视图) Fig. 2 Hydrofoil-pentamaran(Elevation) |
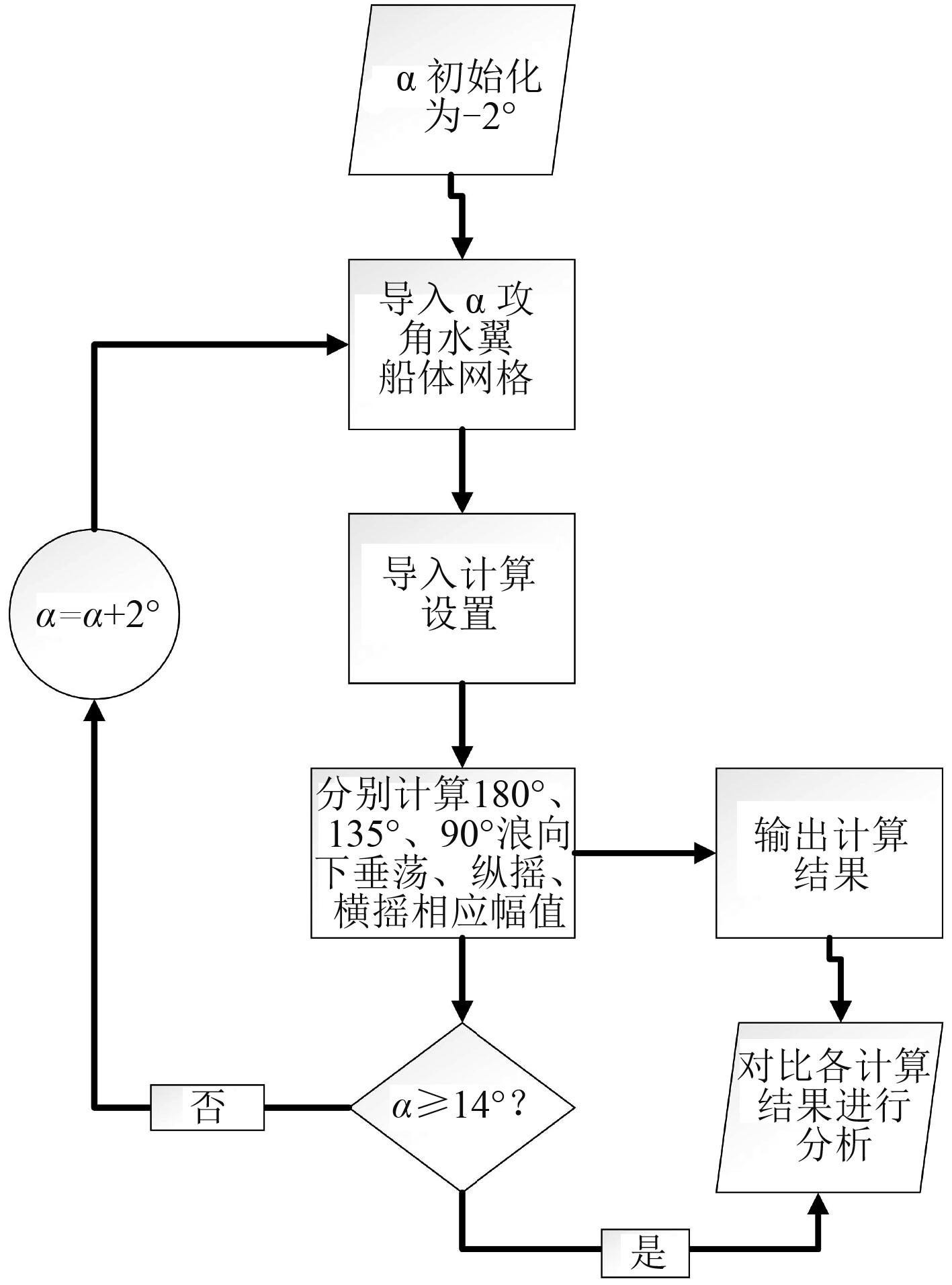
本文主要研究加装不同攻角水翼对五体船耐波性的改善,选择前水翼出水状态进行比较分析,故用小波浪海况进行计算,这里选取有义波高为 1 m 的非规则波作为计算海况。分别计算迎浪、斜浪和横浪 3 种浪向下-2°~14° 范围内各标的攻角水翼五体船耐波性指标,进行对比分析。分析计算流程如图 3 所示。
|
图 3 分析计算流程 Fig. 3 Analysis flow chart |
考虑到前后水翼的升力作用主要对垂荡、纵摇及横摇产生影响,下文便从垂荡、纵摇及横摇 3 个方面进行参数化分析。
为了便于不同尺寸模型对比分析,这里分别引入标准化变量垂荡响应因子HP、纵摇响应因子PP 和横摇响应因子RP:
| $ \begin{array}{l} {H_P} = \frac{H}{L}\text{,}\\[4pt] {P_P} = \frac{P}{L}\text{,}\\[4pt] {R_P} = \frac{R}{L}\text{。} \end{array} $ |
其中:L 为主船体船长,m;H 为垂荡响应幅值,m;P 为纵摇角度幅值,(°);R 为横摇角度幅值,(°)。
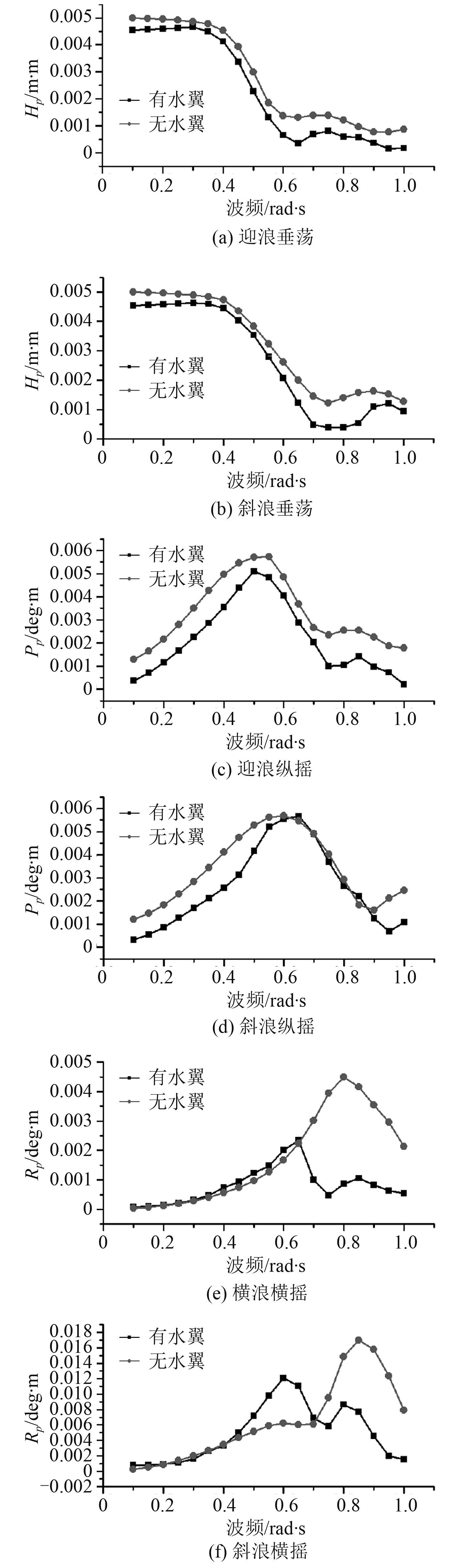
3.1 水翼五体船与五体船耐波性对比分析当相对低速时,NACA4415 翼型的失速攻角为 14°,且在-2°~14° 范围内升力系数随攻角增大而增大[13],这里选取中值 6° 攻角作为水翼五体船代表与五体船进行耐波性指标对比,计算结果如图 4 所示。
|
图 4 水翼五体船和五体船运动响应 Fig. 4 The motion responses of hydrofoil-pentamaran and normal petamaran |
由图 4 可看出,对于垂荡和纵摇,无论在迎浪还是斜浪情况下,水翼五体船响应因子明显低于五体船,这是由于在垂荡和纵摇时 2 个前水翼同时增加或减少入水比例,对应增加或减少相对升力指数,增强回复力,使得垂荡及纵摇回复性能得到明显改善。对于横摇,在高频波段水翼五体船响应因子明显低于五体船,但在低中频波段改善情况不显著,这可能是由于横倾时左右水翼出水不一致,导致低频波周期与船体自身横摇周期相接近,引起共振效应抵消了水翼带来的回复力增加值,而高频波周期远小于船体横摇周期,共振效应不明显,回复力增加减小横摇幅值。总体来说,加装水翼构造的水翼五体船相对五体船耐波性可以得到明显提高。
3.2 水翼五体船最优攻角分析据长周期统计,波浪周期在 11 s 以下的概率为 96.17%,其中波浪周期在 7~9 s 范围内出现频率最高,可达 35.87%[13]。这里对选取 0.15 rad/s 波浪下为分析对象,进行最优攻角分析,计算结果如图 5 所示。

|
图 5 各攻角水翼五体船运动响应 Fig. 5 The motion responses of hydrofoil-pentamaran with different hydrofoil angles |
由图 5 可看出,在攻角-2°~14° 范围内,不同攻角对垂荡、纵摇和横摇的影响走势相同。总体来看,攻角角度较小时随着攻角的增大各响应幅值呈减小趋势,但在 10° 以后,随着攻角的增大,各响应幅值又随之增加。水翼对耐波性的影响由其产生的升力造成,在-2°~14° 攻角范围内升力系数随攻角增大而增大[12],升力系数增加直接致使水翼升力对耐波性的改善力度增加,垂荡、纵摇及横摇时回复力矩增大,响应幅值减小;但 NACA4415 翼型的失速攻角为 14°,在静浮攻角接近失速角时,随船舶在波浪中姿态的改变,实际攻角有可能会超过失速角,致使整体升力期望值下降,对耐波性的改善程度亦会随之减小。另外,在不同浪向下不同攻角对耐波性的改善情况走势一致,这是由于水翼所产生的升力变化仅与船舶姿态及攻角直接相关,而与外部波浪情况相关度不大。综合来看,计算结果与理论预期相吻合,对于 NACA4415 翼型水翼五体船最优攻角在 10° 左右。
4 结 语本文基于 HydroSTAR 软件通过数值模拟的方法对比分析了加装水翼构造水翼五体船对耐波性的改善情况,并通过不同水翼攻角的对比分析得出了 NACA4415 翼型水翼五体船最优攻角。通过计算分析发现,加装水翼可以明显降低垂荡、纵摇及横摇的响应幅值,在低频波段 NACA4415 翼型水翼五体船最优攻角在 10° 左右。
本文是对水翼五体船耐波性优化的初步研究,基于经典 Wigley 船型及水翼船通用 NACA4415 翼型,对于不同船型及不同翼型的组合最优攻角可能会有所差别,对此有待进一步研究。
| [1] | GEE N, DUDSON E, STEIGER H. The pentamaran-A new hull concept for fast freight and car ferry applications[C]//The 13th Fast Ferry International Conference. Singapore, 1997. |
| [2] | DUDSON E, GEE N. Optimisation of the seakeeping and performance of a 40 knot Pentamaran container vessel[C]//Proceedings of the 6th International Conference on Fast Sea Transportation FAST2001, I. 2001. |
| [3] |
王泽鸿, 柳存根, 周翀剑, 等. 应用五体船型降低集装箱船EEDI[J]. 船舶工程, 2014 (4): 003.
WANG Ze-hong, LIU Cun-gen, ZHOU Cheng-ju, et al. Application of pentamaran to reduce EEDI of container ship[J]. Ship Engineering, 2014 (4): 003. |
| [4] |
贺俊松, 陈震, 黄小平, 等. 五体船纵向运动预报的一种工程算法及其在前侧体位置优化中的应用[J]. 船舶力学, 2008, 3 (3): 009–387.
HE Jun-song, CHEN Zhen, HUANG Xiao-ping, et al. An engineering method for predicting the longitudinal motion of pentamaran and its application in the fore sponsons' positional optimization[J]. Journal of Ship Mechanics, 2008, 3 (3): 009–387. |
| [5] |
彭斌. 船舶节能技术综述[J]. 舰船科学技术, 2005, 27 (S1): 3–6.
PENG Bin. Prospects for super energy-saving ship[J]. Ship Science and Technology, 2005, 27 (S1): 3–6. |
| [6] |
徐敏, 张世联. 三体船/五体船的运动及波浪载荷[J]. 大连海事大学学报(自然科学版), 2011, 37 (3): 1–4.
XU Min, ZHANG Shi-lian. Motions and wave loads of trimaran and pentamaran[J]. Journal of Dalian Maritime University, 2011, 37 (3): 1–4. |
| [7] | CALKINS D E. HYCAT:hybrid hydrofoil catamaran concept[J]. Ocean Engineering, 1984, 11 (1): 1–21. DOI: 10.1016/0029-8018(84)90021-0 |
| [8] | CALKINS D E. Development of HYCAT[M]. 1986: 86-2381. |
| [9] |
罗少泽, 马宁, 顾解忡, 等. 五体船阻力与耐波性协同优化方法研究[C]//2013年船舶水动力学学术会议论文集, 2013.
LUO Shao-ze, MA Ning, GU Xie-chong, et al. Research on collaborative optimization for resistance and seakeeping performance of a pentamaran[C]//2013 Ship Hydrodynamics Academic Conference, 2013. |
| [10] | LIU S L. Numerical simulation of large amplitude ship motions and applications to ship design and safe operation[J]. 2011. |
| [11] | KATAM V, LEBEAU R P, JACOB J D. Experimental and computational investigation of a modified NACA 4415 in low-Re flows[C]//22nd Applied Aerodynamics Conference and Exhibit. 2004:4972. |
| [12] |
曲立群, 汪建文, 朱德臣, 等. NACA4415翼型失速特性的二维数值研究[J]. 内蒙古工业大学学报(自然科学版), 2009 (1): 008.
QU Li-qun, WANG Jian-wen, ZHU De-chen, et al. A two-dimensional numerical study on stall of NACA4415 airfoil[J]. Journal of Inner Mongolia University of Technology (Natural Science), 2009 (1): 008. |
| [13] |
毛筱菲, 唐卫军, 熊云峰, 等. 舰船耐波性设计及其评价指标的计算[J]. 中国舰船研究, 2006, 1 (1): 41–45.
MAO Xiao-fei, TANG Wei-jun, XIONG Yun-feng, et al. Seakeeping design and calculation of the ship performance index[J]. Chinese Journal of Ship Research, 2006, 1 (1): 41–45. |
 2017, Vol. 39
2017, Vol. 39
