2. 高新船舶与深海开发装备协同创新中心, 上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
双体船是由 2 个细长的片体组成,片体上部用连接桥连接在一起。其作为一种新型的船型,相对于传统双体船而言具有甲板面积大、稳性好、兴波阻力小等优势[1],并且随着铝制材料广泛运用到船舶建造中,使得铝制双体船相对于普通钢质船舶具有诸多优点,比如结构重量轻、易于加工、相同的排水量可以多装载。相等的航速下所需要的推进功率比钢船低、其耐腐蚀能力和在低温海域的抗裂性能远高于钢质船舶等[2]。
双体船相对于单体船宽度较大,结构更为复杂,其在波浪中航行时,整船不仅受到顺浪和逆浪船体产生的纵向弯曲力矩,还受到由于左右片体相对横摇而产生的横向弯矩和纵摇产生的纵向转矩[2],所以对双体船的强度评估不仅要考虑总纵强度,还要考虑船体的扭转强度以及横向强度问题。而且,铝合金材料在焊接后屈服强度较低的劣势,使得铝制高速双体船的强度校核与评估尤为重要。
1 双体船结构强度评估有限元方法双体船结构强度评估的有限元方法是建立全船的有限元模型,由模型实验法或者规范给定的公式确定载荷条件,或者采用基于流体力学理论的直接计算法确定波浪载荷[2-4],并以实际情况施加到有限元模型上,模拟最佳的双体船受力情况,通过大规模有限元分析求解,最后得到船舶在不同工况下结构的应力结果。
双体船强度有限元分析中,为了反映船舶真实的受力情况,施加的外载荷需包括重力、舷外静水压力和波浪载荷。重力可采用分布质量处理,即根据单元的质量密度参数,由程序自动处理和分配到相关的节点上去;舷外静水压力以面压力的形式加载,即根据计算工况的吃水情况,建立相应的压力场函数,再分配到船体外板湿表面上[5];波浪载荷计算相对而言比较复杂。
实际双体船在波浪中航行,一方面会受到波浪冲击力的影响而在不同剖面产生较大的总纵弯矩;另一方面,由于双体船自身具有较大的侧面积以及型深,横浪下很有可能受到较大的横向波浪载荷;此外,当双体船处于斜浪状态,还会由于 2 个片体摇摆运动的不同步,受到纵摇扭矩和横摇扭矩[6]。因此在有限元计算分析中,需要模拟 3 种波浪载荷情况,即确定总纵弯矩,总横弯矩和总扭矩大小,其数值以及分布可参照《海上高速船入级与建造规范 2012》[3](以下简称《规范》)相关规定。
船中中拱的总纵弯矩计算公式为:
| $ \begin{split} & {M_{BY}} = 0.5(1 + \frac{{{a_{cg}}}}{g})(0.25L - \\ & S0.175\frac{\Delta }{{{B_s}d}}(1 + 0.2\frac{{{a_{cg}}}}{g}))\Delta g\text{。} \end{split} $ | (1) |
式中:acg 为重心处的垂向加速度,m/s2;L 为规范船长,m;d 为设计吃水,m;Δ 为排水量,t;BS 为船首尾出水,波峰冲击船中区域底部时冲击面积的宽度,m
总纵弯矩沿船长分布可按照给定的分布曲线施加到全船有限元模型的纵向主要构件上,如舷侧、纵舱壁、船底中纵桁或其他纵桁上,其值大小沿船长方向变化。
对于沿海营运限制的船长小于 50 m 的常规双体船,船中纵剖面处的横向弯矩为:
| $ {M_{BX}} = 0.135\Delta {a_{cg}}b\text{,} $ | (2) |
其中,b 为片体间距,m。
总横弯矩具体是以横向对开力Fy 的形式施加到结构模型上,横向对开力的大小主要取决于总横弯矩的大小以及所施加的位置。根据船模在水池中的实验结果可知这种横向对开力即侧向力的合力作用位置大约为整船吃水的 1/2 处[7]。所以其值为:
| $ {F_y} = \frac{{{M_{BX}}}}{{z + 0.5d}}\text{,} $ | (3) |
其中,z 为设计水线至连接桥中横剖面中和轴的距离,m。
对于沿海营运限制的双体船,总扭矩计算值为:
| $ {M_{ty}} = 0.075\Delta {a_{cg}}L\text{。} $ | (4) |
扭矩Mty 可用片体半船长上反对称分布的均匀载荷p 等效,即同一片体以中横剖面为界前后载荷方向相反,左右片体的载荷方向相反,于是等效均布载荷p 为:
| $ p = \frac{{4{M_{ty}}}}{{{L^2}}}\text{。} $ | (5) |
在有限元模型中,均布载荷以一系列集中力的形式施加在纵向主要构件上。
静力载荷和波浪载荷施加完之后,即可根据规定的工况采用通用有限元软件 MSC.Nastran 求出双体船的结构应力,并对应力结果进行校核分析。
2 若干关键点研究 2.1 总纵弯矩的分布曲线总纵弯矩的分布曲线是为了确定船舶在中拱或中垂条件下沿船长波浪弯矩的分布情况。在实际工程计算中可参照《LR 客船结构强度直接计算指南》推荐的方法[8]。其分布载荷P(x)(向下为正)和由其产生的弯矩分布BM(x)的计算公式为:
| $ \begin{split}\\[-12pt] & P(x) = \frac{{{M_{wo}}}}{{L_{ext}^2}}(20{\alpha _1}{x^3} + 12{\alpha _2}{x^2} - \\ & \quad \quad \quad \quad 6(2{\alpha _2} + 3{\alpha _1})x + 2(2{\alpha _1} + {\alpha _2})){\rm {kN/m}}\text{,} \end{split} $ | (6) |
| $ \begin{split}\\[-12pt] & BM(x) = {M_{wo}}({\alpha _1}{x^5} + {\alpha _2}{x^4} - \\ & \quad \quad \quad \quad (2{\alpha _2} + 3{\alpha _1}){x^3} + (2{\alpha _1} + {\alpha _2}){x^2}){\rm {kN/m}}\text{。} \end{split} $ | (7) |
其中,Mwo 为船中处的垂向波浪弯矩;Lext 为船的总长;
| $ \begin{aligned} {a_1} = & \frac{{{A_{22}} - {A_{12}}}}{{{A_{11}}{A_{22}} - {A_{21}}{A_{12}}}}\text{,}\\ {a_2} = & \frac{{{A_{21}} - {A_{11}}}}{{{A_{12}}{A_{21}} - {A_{11}}{A_{22}}}}\text{。} \end{aligned} $ |
而a1,a2 计算中:
| $ \begin{aligned} {x_1} =& \frac{{\alpha + 0.4}}{{\alpha + \beta + 1}}\text{,}\\ {x_2} = & \frac{{\alpha + 0.65}}{{\alpha + \beta + 1}}\text{,}\\ {A_{11}} = & x_1^5 - 3x_1^3 + 2x_1^2\text{,}\\ {A_{22}} = & x_2^4 - 2x_2^3 + x_2^2\text{,}\\ {A_{12}} = & x_1^4 - 2x_1^3 + x_1^2\text{,}\\ {A_{21}} = & x_2^5 - 3x_2^3 + 2x_2^2\text{。} \end{aligned} $ |
其中:α 为从船尾端部到尾垂线的距离与船长L 的比值,β 为从首垂线到船首端部的距离与船长L 的比值。
在《规范》中,总纵弯矩沿船长按正弦分布,弯矩分布公式为:
| $ M(x) = {M_{BY}}\sin \frac{{\pi x}}{L}{ \rm {kN/m}}\text{,} $ | (8) |
其中MBY 为船中横剖面的总纵弯矩;x 为自船尾起算的横截面的纵坐标。
M(x)可通过施加沿船长分布的垂向力q(x)实现,q(x)(向上为正)可按下式计算:
| $ q(x) = \frac{{46}}{{{L^2}}}{M_{BY}}(\sin \frac{{\pi x}}{L} - 0.637){ \rm {kN/m}}\text{。} $ | (9) |
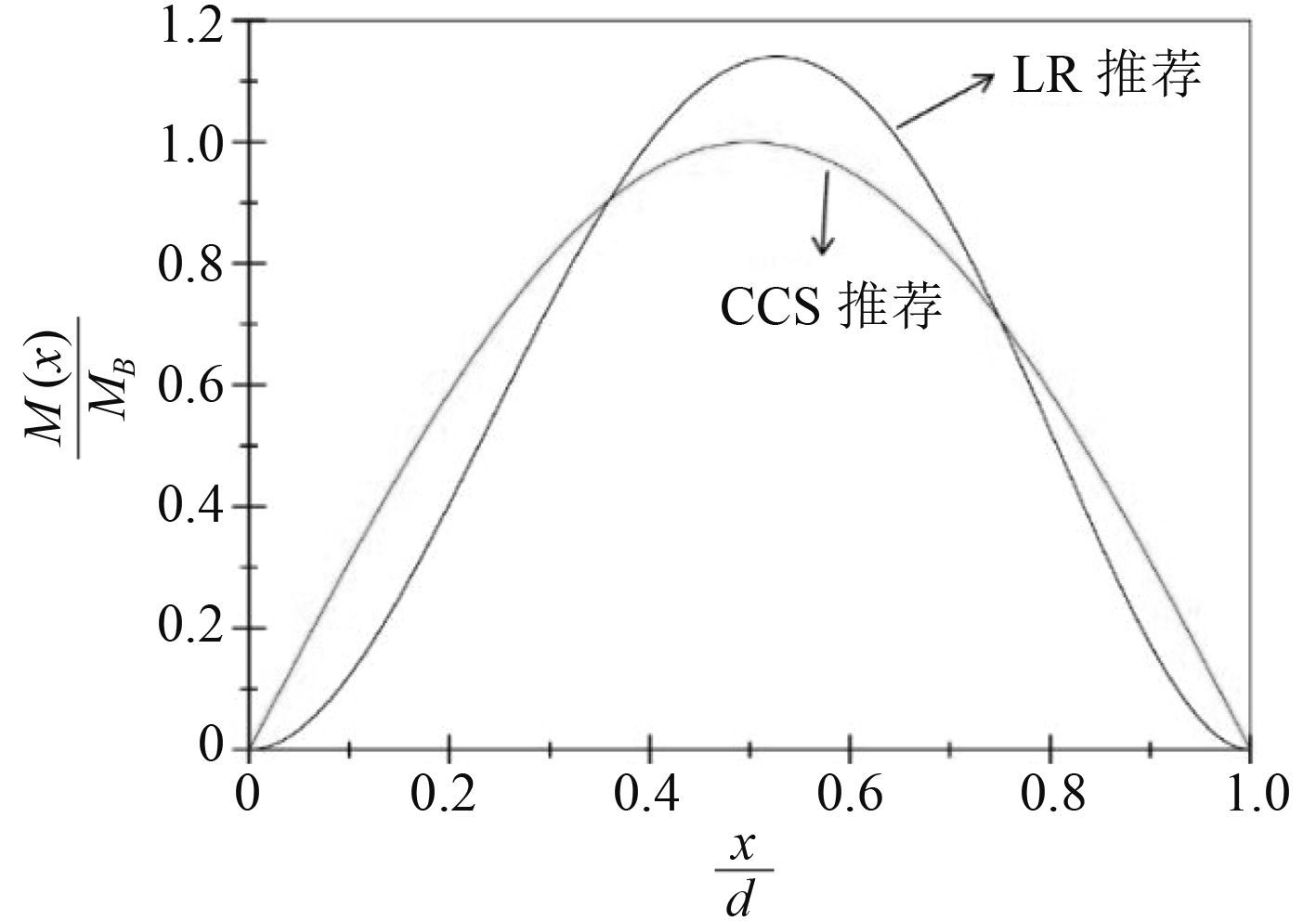
以 1 艘海洋监测高速铝制双体船为研究对象,以自船尾算起距 0 号肋位距离与船长的比值为横坐标,以总纵弯矩与中横剖面的总纵弯矩的比值为纵坐标,作出总纵弯矩曲线分布对比图,如图 1 所示。可以看出,在船中附近,CCS 推荐的方法计算得到的总纵弯矩值要略大于 LR 推荐的方法,而船首和船尾附近则相反。
|
图 1 总纵弯矩曲线分布对比图 Fig. 1 The comparison of longitudinal bending moment curves |
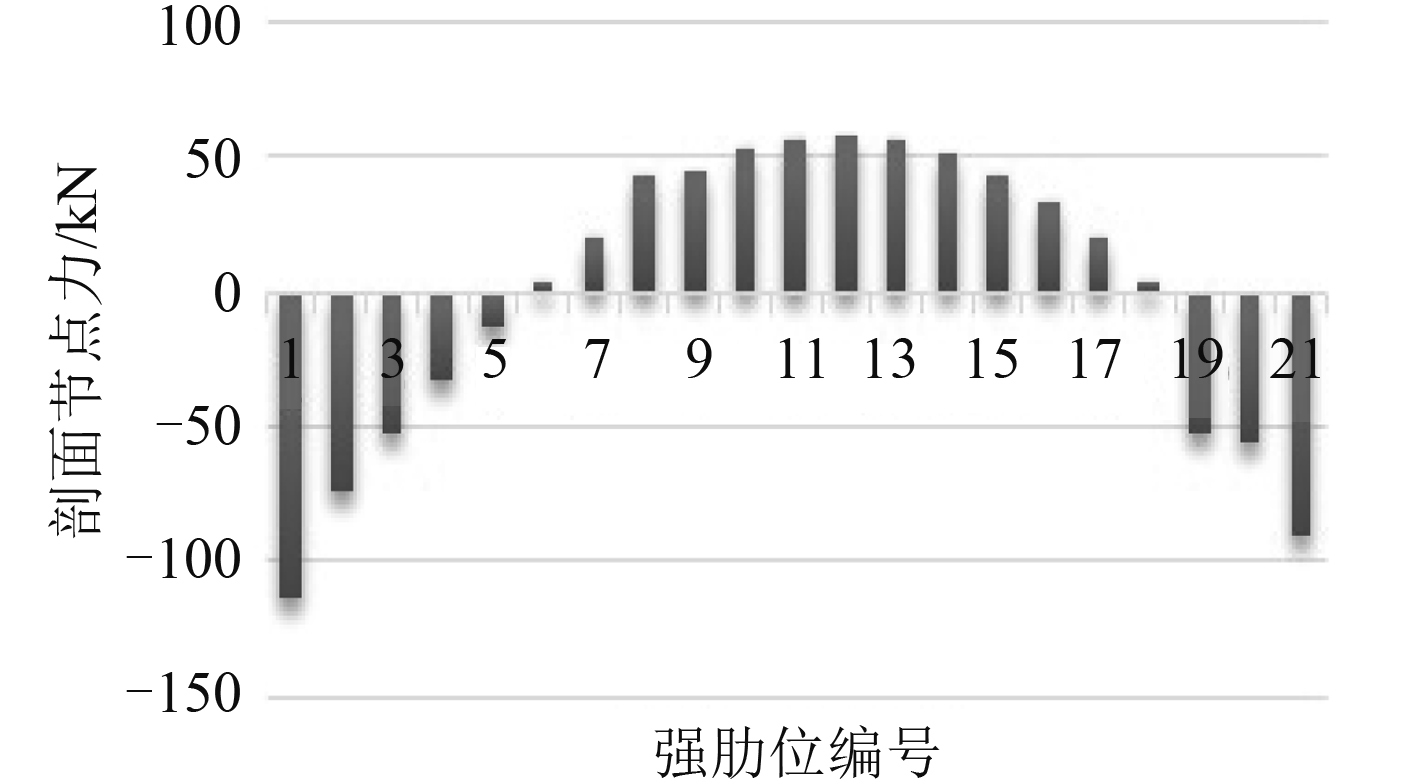
在有限元模型中,分布载荷P(x)或q(x)都是以与之等效的一系列集中力F 施加在强框架肋位的剖面节点上的,中拱强肋位剖面节点力如图 2 所示。分别采用 2 种方法计算该双体船的总纵强度,计算结果如表 1 所示。可以看到,采用 CCS 推荐的方法与 LR 推荐的方法计算得到的板单元正应力以及板单元的剪切应力的误差都在 10% 以内,故认为在校核该双体船的总纵强度时,采用 CCS 或者 LR 推荐的方法都可以。
|
图 2 中拱时不同横剖面等效节点载荷(CCS 推荐方法) Fig. 2 Equivalent nodal forces of different transverse section when hogging(recommended by CCS) |
|
|
表 1 全船不同肋位分段应力比较 Tab.1 The comparison of stresses in different fragments of the whole ship |
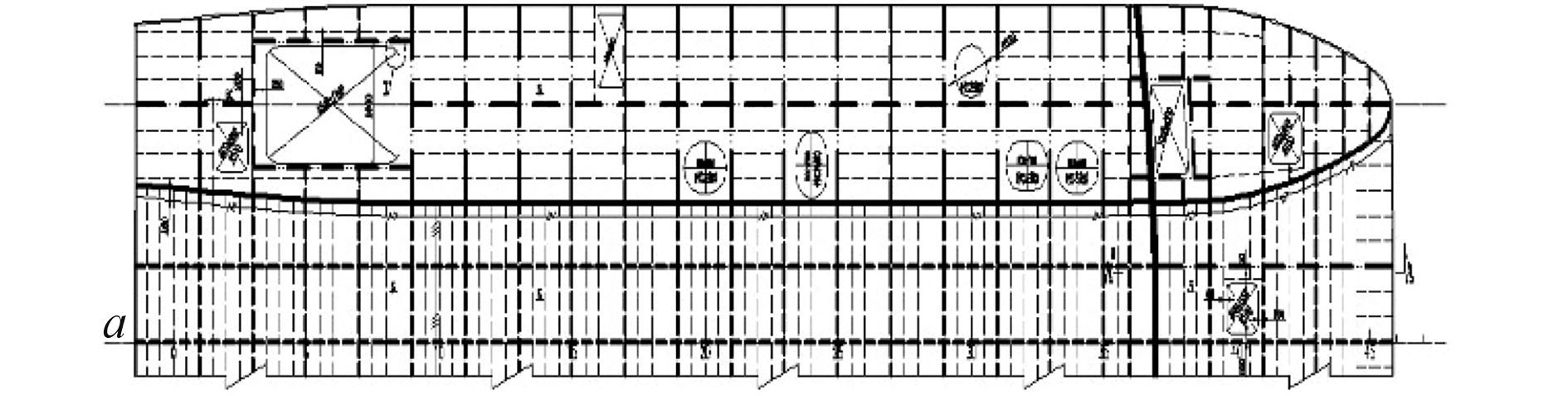
在计算模型中,总扭矩以分布力或等效的集中力的形式施加在纵向主要构件上,例如舷侧、纵舱壁、船底中纵桁或者其他纵桁上,力的作用位置应避免产生构件的局部弯曲应力,规范给出了一种施加在上甲板中心线位置的办法。但是若双体船甲板有较多的开口,如图 3 所示,则不便施加在该位置,需要寻找其他施加位置。
|
图 3 主甲板结构图 Fig. 3 The structure plan of main deck |
实际分布力或集中力分别加载在不同位置时,对结构产生的应力大小各有不同。究其具体原因,一方面是不同位置结构组成不同,应力传递程度不相同,另一方面施加位置距离船舶中心线的远近影响了分布力或集中力对整船产生的弯矩大小。
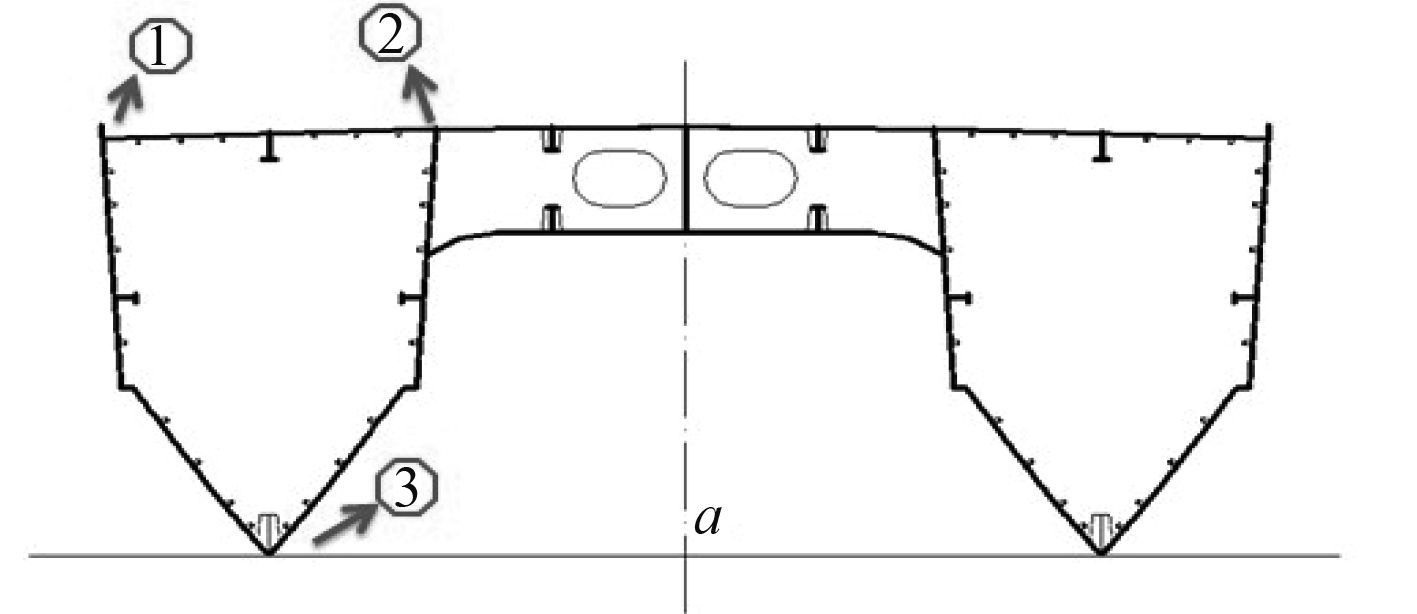
以海洋监测高速铝制双体船为研究对象,给出了 3 种典型加载位置:上甲板外舷侧、上甲板内舷侧以及船底中纵桁,如图 4 所示。通过 Nastran 计算得到应力结果,如表 2 所示。
|
图 4 总扭矩应力加载位置 Fig. 4 The loading locations of total torque |
|
|
表 2 三种方案应力结果 Tab.2 The stress results of three plans |
比较上表结果可以看出,3 种方案得到板单元正应力以及板单元剪切应力计算结果相差较小,误差小于 10%。方案 2 的应力计算结果略大于其他 2 种方案,偏于安全,本文推荐采用方案 2。
3 全船结构强度分析铝合金高速海洋监测船的主尺度为:船长LOA = 23.640 m;型宽B = 8 m;型深D = 2.65 m;设计吃水d = 1.25 m;排水量 Δ = 76.3 t。如图 5 所示。
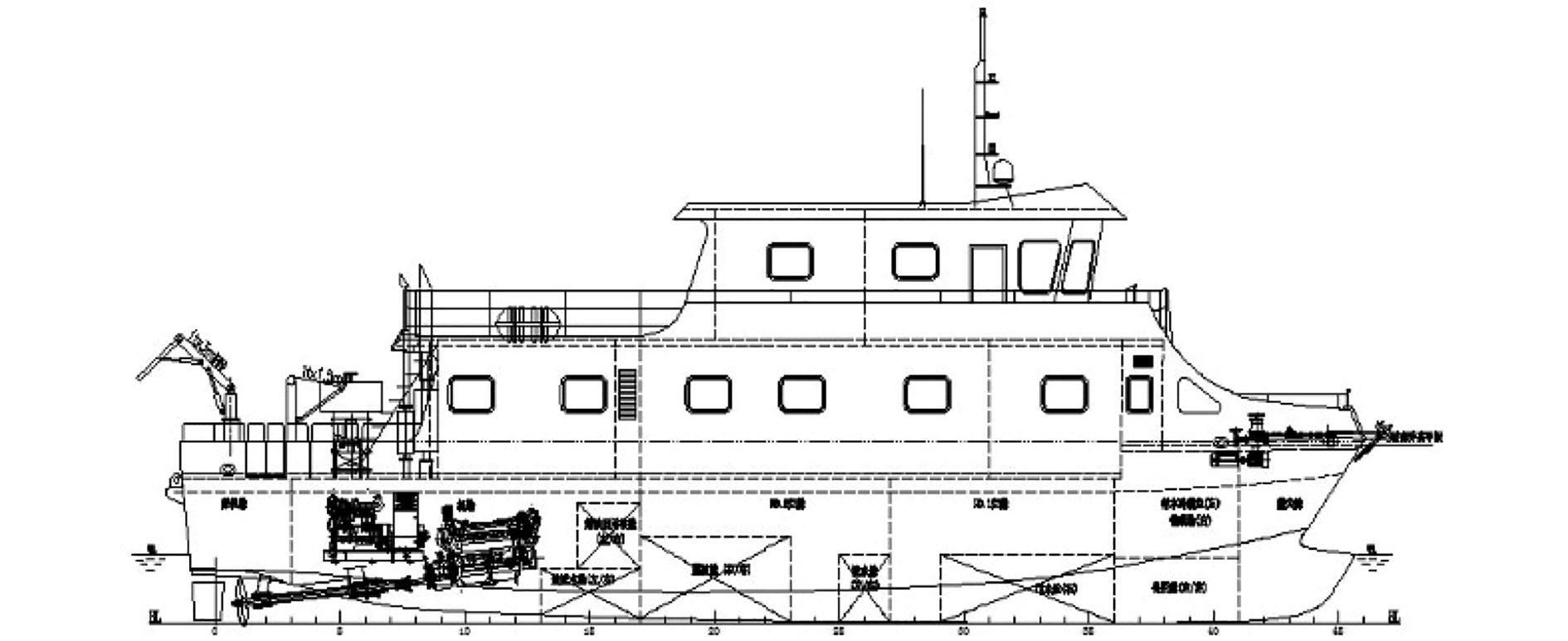
|
图 5 总布置侧视图 Fig. 5 The side view of general arrangement |
建立全船有限元模型,分别施加总纵弯矩、总横弯矩、总扭矩以及静力载荷。其中总纵弯矩的分布曲线可以参照《规范》要求,总扭矩的施加位置可选取 2.2 方案 2 所选的位置。提出 12 种工况,如表 3 所示,覆盖了总纵弯矩、总横弯矩、总扭矩以及它们的组合情况。其中Mp 表示总扭矩。
|
|
表 3 计算工况 Tab.3 Load cases |
通过全船结构有限元计算分析,在各计算工况下,船体结构板单元相当应力、板单元剪切应力、梁单元相当应力的最大应力值如表 4 所示,单位为 N/mm2,对应的部分全船结构应力计算结果云图如图 6和图 7 所示。其中应力许用值参考《规范》。
|
|
表 4 双体船全船板单元应力计算结果 Tab.4 The results of plate element stresses of the whole catamaran |

|
图 6 Von-Mise 应力云图 Fig. 6 The Von-Mise stress nephogram |
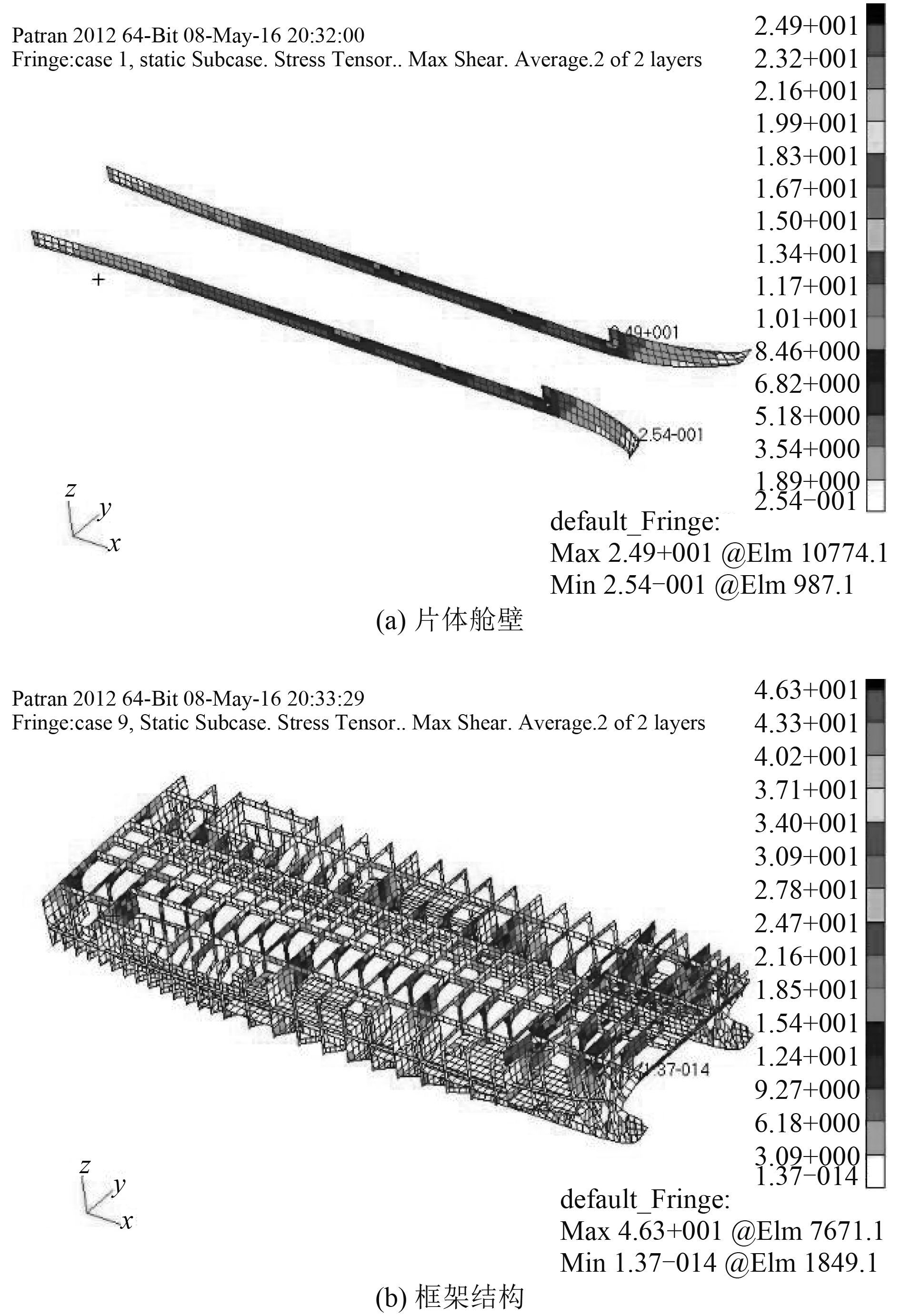
|
图 7 Max Shear 应力云图 Fig. 7 The max shear stress nephogram |
从表中的计算结果可以看出,本船的板单元相当应力和剪切应力均小于许用应力,满足衡准要求,能保证船舶的各种强度要求。12 种工况中 LC3 和 LC9 板单元的相当应力和剪切应力较大,说明总横弯矩工况及其相应的组合工况是值得关注的载况。在总横弯矩的作用下,连接桥以及其横向结构受力较大,片体相连接部分结构所受剪切应力较大,因此需要对该部分结构进行加强或优化;从图中可以看出,甲板开口处产生了应力集中,应力较大,在结构设计时应考虑这些因素。
4 结 语本文系统阐述高速铝制双体船的强度评估方法。以 1 艘高速铝制海监船为例,探究总纵弯矩的分布曲线、总扭矩施加位置选取的不同,对船舶计算强度的影响,并基于较危险的载荷施加方式对全船强度作出了评估。用有限元方法评估双体船总纵强度时,可以采用 CCS 或 LR 推荐的总纵弯矩分布曲线,2 种方法均可行。在施加扭矩时,推荐采用文中方案 2 即施加在上甲板内舷侧内侧的位置。本文选用 12 种工况进行全船有限元分析,得到了各典型工况下船体结构的应力分布特点,可为同类双体船的结构初步设计提供参考。
| [1] |
崔连琼, 吴诗寒, 禚茜萍, 等. 非高速双体船波浪载荷直接计算方法研究[J]. 中国水运, 2015, 15 (8): 21–23.
CUI Lian-qiong, WU Shi-han, ZHUO Qian-ping, et al. The research of direct calculation method for wave loading of non-high-speed catamaran[J]. China Water Transport, 2015, 15 (8): 21–23. |
| [2] | 管义锋, 黄涣青, 谷家扬, 等. 双体铝合金高速客船强强度有限元分析研究[J]. 船舶工程, 2011, 33 (6): 14–17. |
| [3] | 中国船级社. 海上高速船入级与建造规范[M]. 北京: 人民交通出版社, 2012. |
| [4] | 江雪云, 冯国庆, 张清越, 等. 小水线面双体船波浪载荷预报研究[J]. 船舶工程, 2015, 37 . |
| [5] |
徐永超, 夏利娟. 半潜驳改装海上风机吊装船结构强度评估[J]. 舰船科学技术, 2014, 36 (5): 11–14.
XU Yong-chao, XIA Li-juan. Research on structural strength evaluation of wind turbine installation vessel retrofitted from semi-submersible barge[J]. Ship science and Technology, 2014, 36 (5): 11–14. |
| [6] |
胡犇, 许晟, 梅国辉, 等. 基于Patran的高速小水线面双体船有限元结构强度分析[J]. 舰船科学技术, 2011, 33 (10): 46–49.
HU Ben, XU Sheng, MEI Guo-hui, et al. Strength analysis of overall ship FEM model based on design wave approach[J]. Ship Science and Technology, 2011, 33 (10): 46–49. |
| [7] | 林吉如, 石理国, 尤国红, 等. 小水面双体船波浪设计载荷估算方法[J]. 中国造船, 2008, 49 (3): 104–111. |
| [8] | LR. Guidance on direct calculations for primary structure of passenger ships[S]. 2004. |
| [9] | 中国船级社. 海上高速船入级与建造规范[M]. 北京: 人民交通出版社, 2005. |
| [10] |
郑杰, 谢伟, 骆伟, 等. 穿浪双体船横向强度与扭转强度的有限元计算[J]. 中国舰船研究, 2010, 5 (1): 14–18.
ZHENG Jie, XIE Wei, LUO Wei, et al. Finite element analysis on the transverse and torsion strength of a wave piercing catamaran[J]. Chinese Journal of Ship Research, 2010, 5 (1): 14–18. |
 2017, Vol. 39
2017, Vol. 39
