IMO 目前正在制定船舶第二代完整稳性衡准相关草案,瘫船稳性薄弱性衡准是 5 个薄弱性衡准中的重要组成。瘫船稳性第 1 层和第 2 层薄弱性衡准草案是由意大利和日本在 SDC1 会议上提出并得到通过的[1]。
当船舶不满足第 2 层薄弱性衡准时须进行第 3 层次的稳性直接评估,目前评估方法尚未形成。美国[2]等国家要求瘫船稳性的直接评估方法至少考虑 5 个自由度(横摇-横荡-垂荡-纵摇-首摇)。但 5 个自由度计算模型复杂,特别是计算船舶倾覆概率时,为达到置信区间可信度要求,计算样本量巨大,这导致目前多自由度计算模型目前尚难以执行。
Kubo 等[3]讨论了横风横浪联合作用下瘫船横摇运动数值模拟方案,提供了单自由度直接模拟方法。该方案模型相对简单,可以大幅缩短计算时间,经过试验验证具有一定的参考性。
本文基于 SDC1/INF.6 中瘫船稳性失效模式薄弱性衡准的单自由度横摇运动模型,对瘫船稳性第 3 层薄弱性衡准直接评估方法进行研究。通过建立瘫船横摇运动单自由度非线性方程,分解求解无风浪情况下的横摇自由衰减运动,以及规则波和不规则风浪联合作用下瘫船横摇运动响应。并进行标准模型 CEHIPAR2792相应试验,将试验数据与计算结果对比,为瘫船稳性直接评估方法研究提出建议。
1 单自由度横摇运动模型考虑非线性的横摇阻尼的横风横浪下单自由度横摇数学模型由如下非线性微分方程描述:
| $ I_{xx}'\ddot \theta + N(\dot \theta ) + D(\theta ) = M\text{,} $ | (1) |
式中:左边第 1 项为惯性力项;I’xx 为船舶横摇总惯性矩。试验模型的横摇惯性矩可根据式(2)求出:
| $ T = 2\pi \sqrt {\frac{{I_{xx}'}}{{\Delta \cdot GM}}} \text{,} $ | (2) |
式(1)中第 2 项为阻尼项。本文基于标准模型 CEHIPAR2792 试验结果发现,当使用线性项加平方项进行拟合时,会出现线性项为负的显然不符合实际情况的结果。当换成线性项加立方项(如式(3)),能够得到理想的拟合结果。
| $ N(\dot \theta ) = {N_1}\dot \theta + {N_3}{\dot \theta ^3}\text{,} $ | (3) |
式(1)中第 3 项为回复力矩项,可由静水力计算结果得到,通常用高次的奇次多项式进行曲线拟合以便编制计算程序。
| $ D(\theta ) = \Delta \cdot \sum\limits_{i = 1}^n {{C_i}{\theta ^{2i - 1}}}\text{,} $ | (4) |
式(1)中的右端为外力作用项,本文计及非定常波浪和风的共同作用。
通过以上分析确定横摇运动方程为:
| $ I_{xx}'\ddot \theta + {N_1}\dot \theta + {N_3}{\dot \theta ^3} + \Delta \cdot \sum\limits_{i = 1}^n {{C_i}{\theta ^{2i - 1}}} = M\text{。} $ | (5) |
回复力矩项的处理主要是针对船舶在大角度横摇时回复力矩项的非线性进行精确的数值拟合。
本文的研究对象是标准模型 CEHIPAR2792,其主尺度如表 1 所示,试验研究船舶模型缩尺比为 1∶65。
|
|
表 1 CEHIPAR2792 模型主尺度 Tab.1 Main Dimensions of Model CEHIPAR2792 |
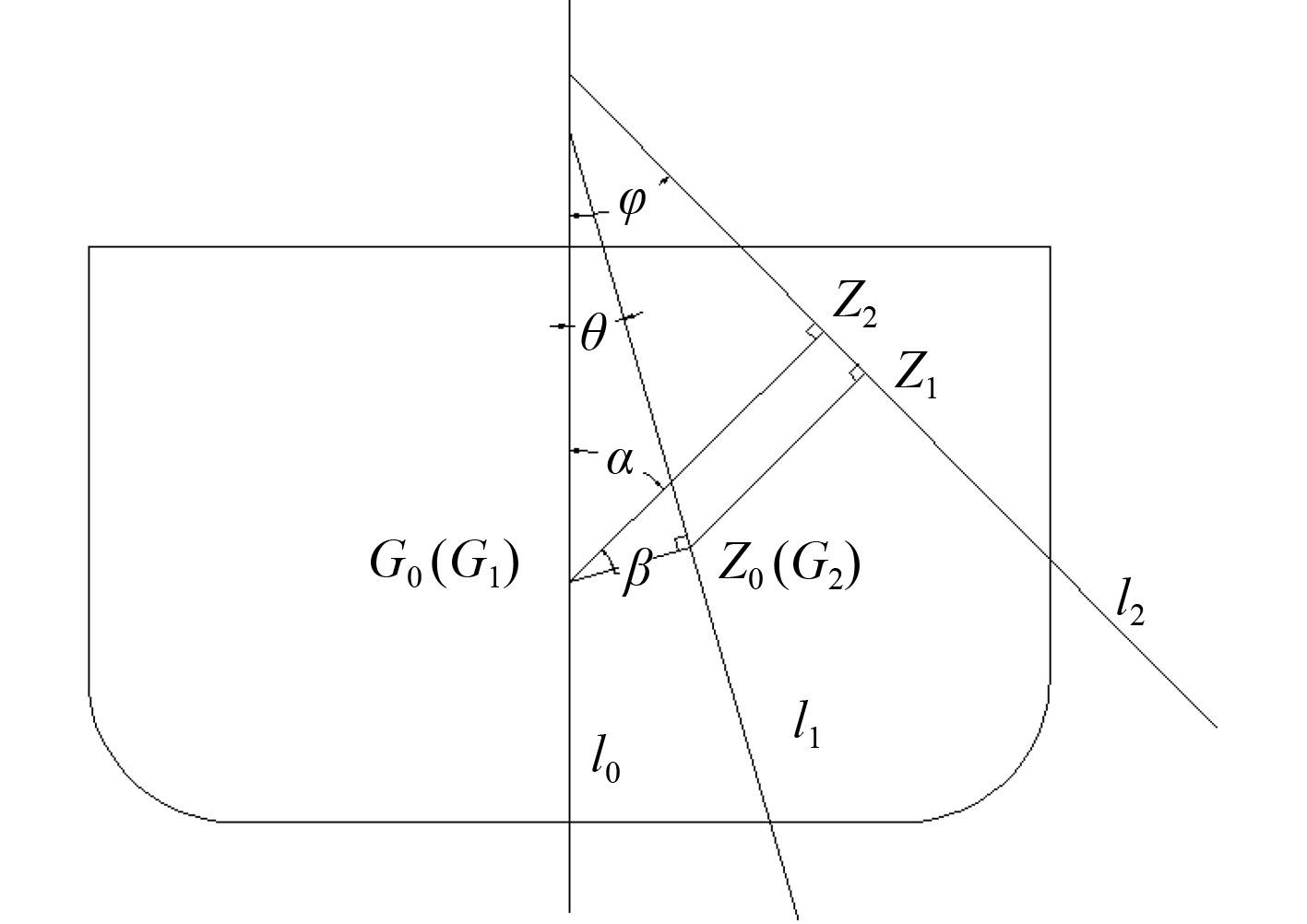
由 SDC1 INF.6 查得该船初始状态正浮时的GZ 曲线。通过几何分析,确定货物移动导致船舶具有初始的固定横倾时的GZ 曲线,其原理如图 1 所示。
|
图 1 货物移动导致的横倾使GZ 改变 Fig. 1 Cargo shift changes theGZ |
如果不考虑货物移动,横倾θ 角时,过重心G0 作l2 的垂线,垂足为Z0;横倾φ 角时,过重心G0(G1)作l3 的垂线,垂足为Z1。考虑货物移动导致了船舶初始横倾了θ 角,重心从G0 移动到G2。本试验中,θ 小于 10°,故考虑Z0 和G2 位置大致相同。则根据图 1 中的几何关系可以得到下式:
| $ \begin{array}{l} \varphi + \alpha = 90^\circ\text{,} \\[5pt] \alpha + \beta + \theta = 90^\circ \text{,}\end{array} $ |
推出
| $ \beta = \varphi - \theta \text{,} $ | (6) |
得到货物移动导致船舶重心发生改变后的船舶静稳性臂曲线表达式:
| $ {G_2}{Z_2} = G{Z_\theta } = {G_1}{Z_1} - GZ(\theta ) \times \cos (\beta ) \text{。}$ | (7) |
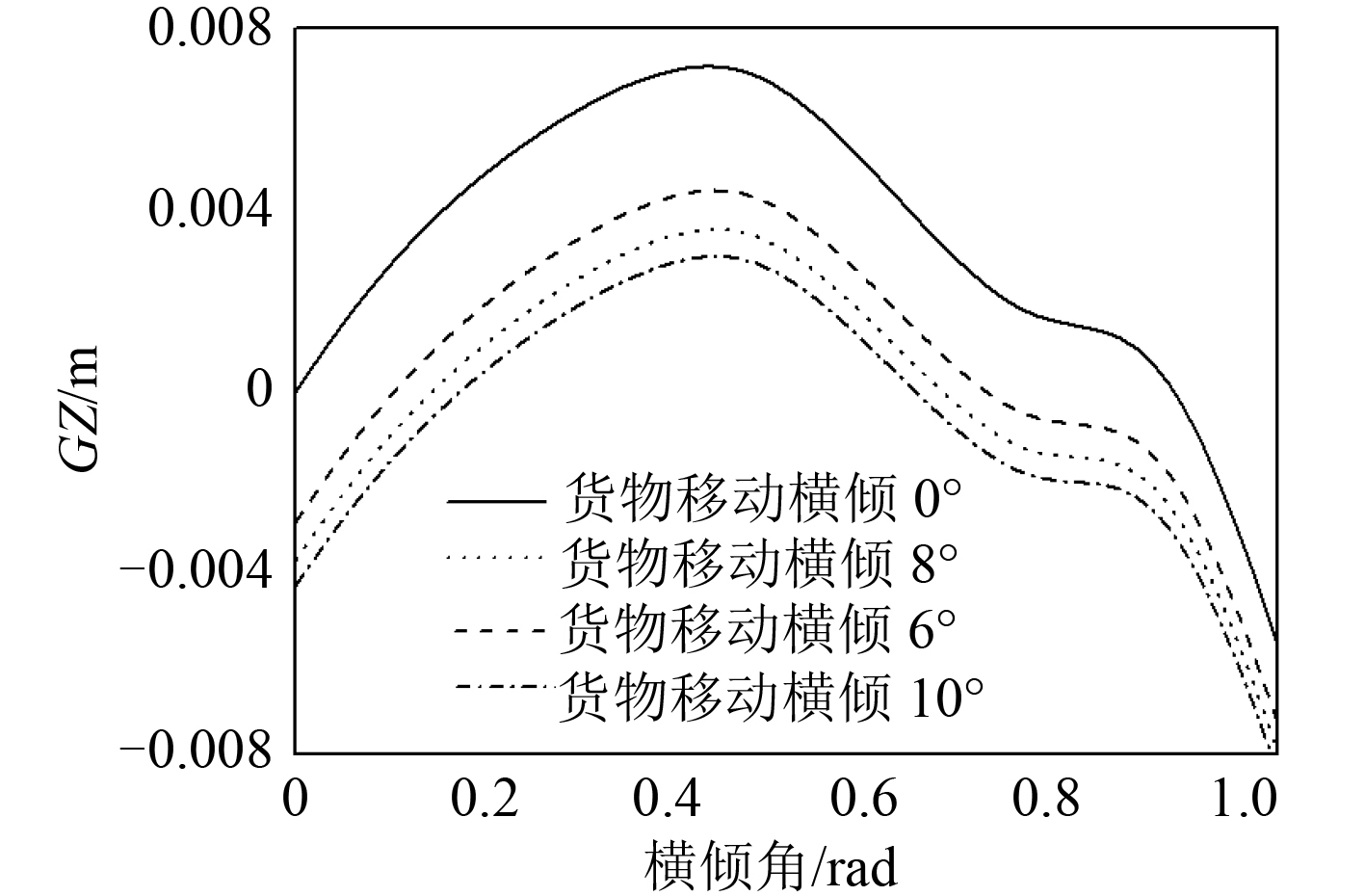
依据式(7)得到货物移动导致不同初始固有横倾状态下的船舶GZ 曲线如图 2 示。该计算结果与 Kubo 等[2]的研究吻合。
|
图 2 不同固有横倾状态下的GZ 曲线 Fig. 2 GZ with different cargo shift |
为了便于编制计算程序,使用最高 15 次的奇次多项式拟合GZ 曲线,船舶正浮状态GZ 曲线拟合结果如图 3 所示。
| $ GZ(\theta ) = \sum\limits_{i = 1}^8 {{C_i}{\theta ^{2i - 1}}} \text{,} $ | (8) |
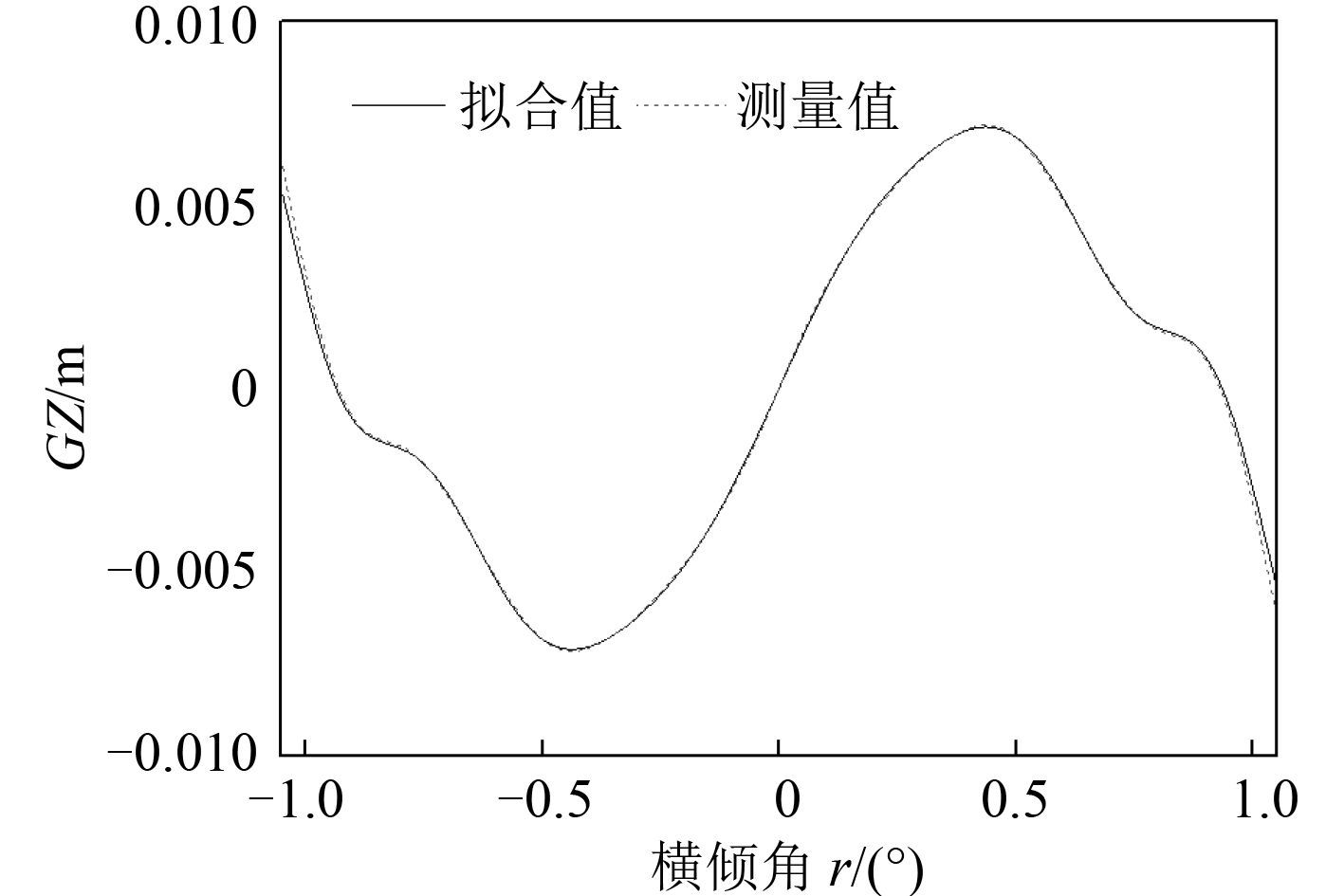
|
图 3 初始状态正浮时的GZ 曲线拟合 Fig. 3 Fitting ofGZ |
其中,Ci 如表 2 所示。
|
|
表 2 无货物移动GZ 曲线拟合系数 Tab.2 Fitting Coefficients ofGZ without cargo shift |
根据式(6),可以进行相应初始固有横倾下的GZ 曲线计算,不需要单独进行拟合。
1.2 能量法求解衰减系数横摇阻尼力矩项的处理,是针对船舶在大角度横摇时阻尼项产生的非线性进行求解。通常采用模型试验得到船舶自由衰减曲线后,用能量法或消灭曲线法获得横摇阻尼力矩系数的方法。本文用线性加立方项的形式定义阻尼力矩项,并采用能量法求解[6]。
定义阻尼力矩为线性加立方项如下:
| $ N(\dot \theta ) = {N_1}\dot \theta + {N_3}{\dot \theta ^3}\text{,} $ | (9) |
横摇过程中三体船的总能量为:
| $ E(t) = \frac{1}{2}{\dot \theta ^2} + \int_0^t {D(\theta )} \dot \theta {\rm d}t \text{。}$ | (10) |
根据能量守恒,损耗的能量用于抵消阻尼力矩所做的功,即
| $ E({t_{i + 1}}) - E({t_i}) = - \int_{{t_i}}^{{t_{i + 1}}} {N(\dot \theta )} \dot \theta {\rm d}t \text{,}$ | (11) |
令
| $ \begin{split} \!\!\!\!\!\!Q({t_i}) = E({t_{i + 1}}) - E({t_i}) = \frac{1}{2}(\dot \theta _{i + 1}^2 - \dot \theta _i^2) + \int_{{t_i}}^{{t_{i + 1}}} {D(\theta )} \dot \theta {\rm d}t \text{,}\end{split} $ | (12) |
将式(8)和式(11)代入式(10)可得:
| $ Q({t_i}) = {N_1}\int_{{t_i}}^{{t_{i + 1}}} {{{\dot \theta }^2}{\rm d}t} + {N_3}\int_{{t_i}}^{{t_{i + 1}}} {{{\dot \theta }^3}\dot \theta {\rm d}t} \text{。} $ | (13) |
其中:等式的左边为δt 时间内总能量的损失;右边为阻尼力矩消耗的功。令
| $ {u_{i1}} = \int_{{t_i}}^{{t_{i + 1}}} {{{\dot \theta }^2}{\rm d}t} ,\;\;\;\;\;{u_{i{\rm{2}}}} = \int_{{t_i}}^{{t_{i + 1}}} {{{\dot \theta }^3}\dot \theta {\rm d}t} \text{,}$ | (14) |
则式(12)可表示为:
| $ Q({t_i}) = {N_1}{u_{i1}} + {N_3}{u_{i{\rm{2}}}} \text{,}$ | (15) |
式(14)可表示为矩阵:
| $ \left[ {\begin{array}{*{20}{c}} {{u_{i1}}} & {{u_{i{\rm{2}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{N_1}}\\ {{N_3}} \end{array}} \right] ={ Q} \text{。}$ | (16) |
式(15)中未知数只有N1 和N3,其余均可用横摇衰减曲线直接计算,应用最小二乘法求解得到该矛盾方程的最小二乘解,取得阻尼力矩系数N1 和N3。
| $ \begin{array}{l} {N_1} = 0.278\text{,}\\[5pt] {N_3} = 1.74\text{。} \end{array} $ | (17) |
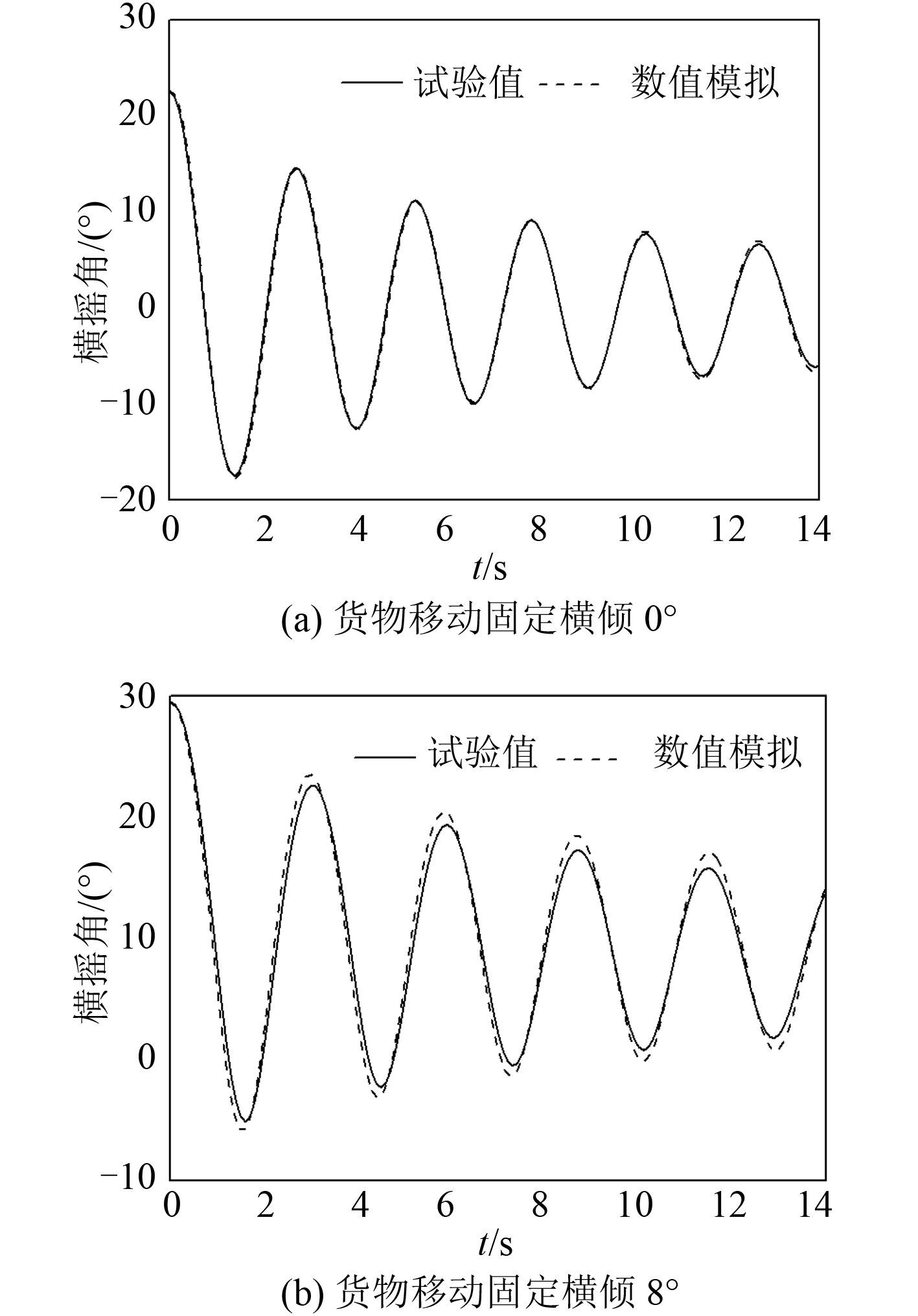
为了验证结果的正确性,令式(1)右端合外力矩项为 0,模拟船舶自由衰减,并与试验值对比如图 4 所示。
|
图 4 模拟自由衰减与实验值对比 Fig. 4 Comparison of numerical and experimental free decay |
计算结果与试验采集数据吻合,验证了横摇阻尼系数和静稳性曲线的计算准确。
2 波浪力矩的计算 2.1 波浪条件试验使用 ITTC 双参数波浪谱,特征周期T = 2.04 s,三一波高H = 0.17 m,对应实际海况为有义波高 11.04 m,特征周期 16.48 s。
随机横浪下单自由度横摇数学模型由如下非线性微分方程描述:
| $ I_{xx}'\ddot \theta + {B_1}\dot \theta + {B_3}{\dot \theta ^3} + \Delta GZ(\theta ) = M $ | (18) |
方程两边同除以I’xx,得
| $ \ddot \theta + {b_1}\dot \theta + {b_3}{\dot \theta ^3} + \frac{\Delta }{{I_{xx}'}}\sum\limits_{i = 1}^8 {{C_i}{\theta ^{2i - 1}}} = m(t)\text{,} $ | (19) |
将式(17)写成 2 个一阶微分方程形式
| $ \left\{ \begin{array}{l} \dot x(t) = y(t)\text{,}\\ \dot y(t) = - {b_1}x(t) + {b_3}{x^3}(t) + \frac{\Delta }{{I_{xx}'}}\sum\limits_{i = 1}^8 {{C_i}{\theta ^{2i - 1}}} + m(t) \end{array} \right.\text{。} $ | (20) |
在随机波浪作用下,波浪激励力矩由线性叠加原理得到。将随机海浪处理为一系列具有随机相位角的简谐波的叠加。本文将根据给出的海浪谱,确定每个简谐波的波浪要素及每个简谐波引起的波浪干扰力矩,进行叠加,得到任意瞬时总的波浪干扰力矩。
基于傅汝德-克雷洛夫和长波近似的假设上将横浪中规则波的横摇干扰力矩为:
| $ M(t) = \Delta GM \cdot {K_\phi }\Theta (t) \text{。}$ | (21) |
式中:Kϕ 为有效波倾系数;KϕΘ(t)为有效波倾。
随机波表示为一系列简谐波的叠加,干扰力矩公式变为:
| $ M(t) = \Delta GM \cdot {K_\phi }\sum\limits_{i = 1}^{{N_W}} {\frac{{{h_i}}}{{{\lambda _i}}}} s{\rm in}({\omega _i}t + {\varepsilon _i}) \text{。}$ | (22) |
式中:hi 为波幅;λi 为横浪的波长;ωi 为波浪频率。
海浪谱就是海浪平稳各态历经过程的能量在频率域中的分布形式。式(20)又可写为:
| $ M(t) = \Delta GM \cdot {K_\phi }\sum\limits_{i = 1}^{{N_W}} {\omega _i^2\sqrt {2{S_{wave}}({\omega _i})\delta \omega } } s{\rm in}({\omega _i}t + {\varepsilon _i})\text{,} $ | (23) |
ITTC 双参数谱:
| $ {S_{wave}}({\omega _i}) = 173{\rm{ }}\frac{{H_{1/3}^2}}{{{T^4}\omega _i^5}}{\rm exp}(\frac{{ - 691}}{{{T^4}\omega _i^4}})\text{。} $ | (24) |
式中:随机相位角εi 在(0-2π)内均匀分布;T 为特征周期;H1/3 为三一波高。
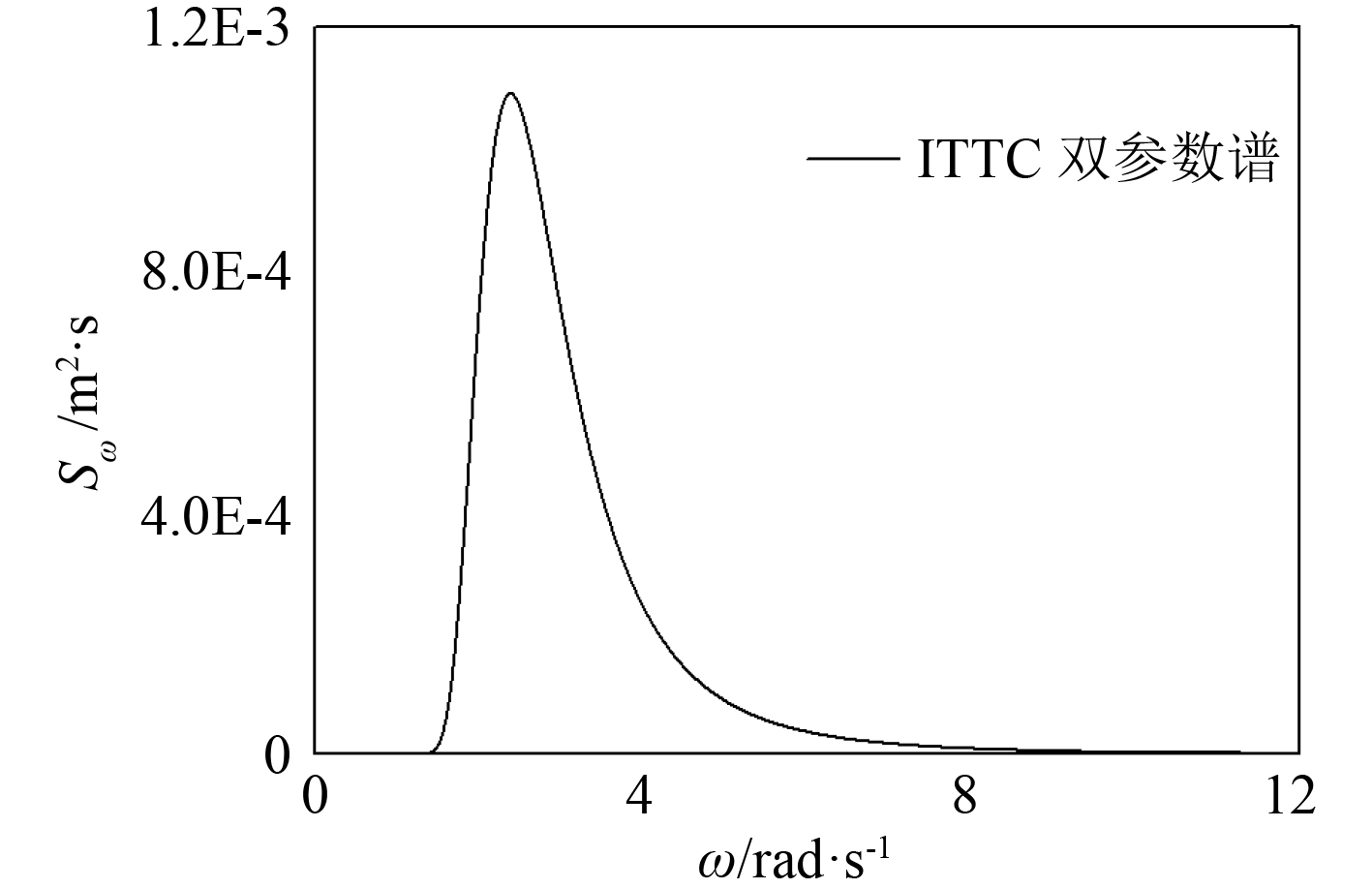
|
图 5 试验采用的 ITTC 谱 Fig. 5 ITTC spectrum used in tests |
有效波倾角αm 和表面波倾角α 存在如下关系[4]:
| $ {\alpha _m} = {K_\phi }\alpha = {K_\phi }{\alpha _0}\sin \omega t = {\alpha _{{m_0}}}\sin \omega t\text{。} $ | (25) |
式中αm0 =Kϕα0,为有效波倾角的幅值,称为有效波倾,它代表对船舶水下体积起作用的波倾,是波浪频率的函数。
对于风浪中的横摇,其响应主要集中在谐摇区的窄频带内,通常用谐摇时的Kϕ 代替整个频率区间的Kϕ 不会引起太大误差。Bulian 等[5]的研究认为,频率小的长波对船体的作用全部有效,有效波倾接近于 1,而频率高的短波作用在船体上几乎可以忽略。将有效波倾系数简化处理,在波长λ =B/2 以下取定值,波长超过这个范围后取 0。
本文根据 SDC1/INF.6 中给出的 CEHIPAR2792 有效波倾测量值数据,在谐摇周期ω = 0.342 rad/s 处取有效波倾系数 0.705,有效波倾系数取值如图 6 所示。计算规则波中的运动时取对应波浪频率下的有效波倾系数。

|
图 6 简化的有效波倾系数 Fig. 6 Simplified effective wave slope coefficient |
风倾力矩的计算式如下(包括定常风和随机阵风):
| $ \begin{array}{l} \frac{{{M_{wind}}(t)}}{{(1 - \sin \phi )}} = 0.5 \times {\rho _{air}}{C_m}U_W^2{A_L}{H_C} +\\ {\rho _{air}}{C_m}U_W{A_L}{H_C}\chi (\omega )U(t)\text{。} \end{array} $ | (26) |
式中:ρair 为空气密度;Cm 为风压倾侧力矩系数[7],取 0.84;UW 为定常风速。U(t) 为 Davenport 风谱[8]描述的非定常风速;AL 为水面以上船舶侧投影面积;HC 为风力作用点距离水动力作用点的高度;χ(ω) 为阵风影响系数。其受力分析如图 7 所示。
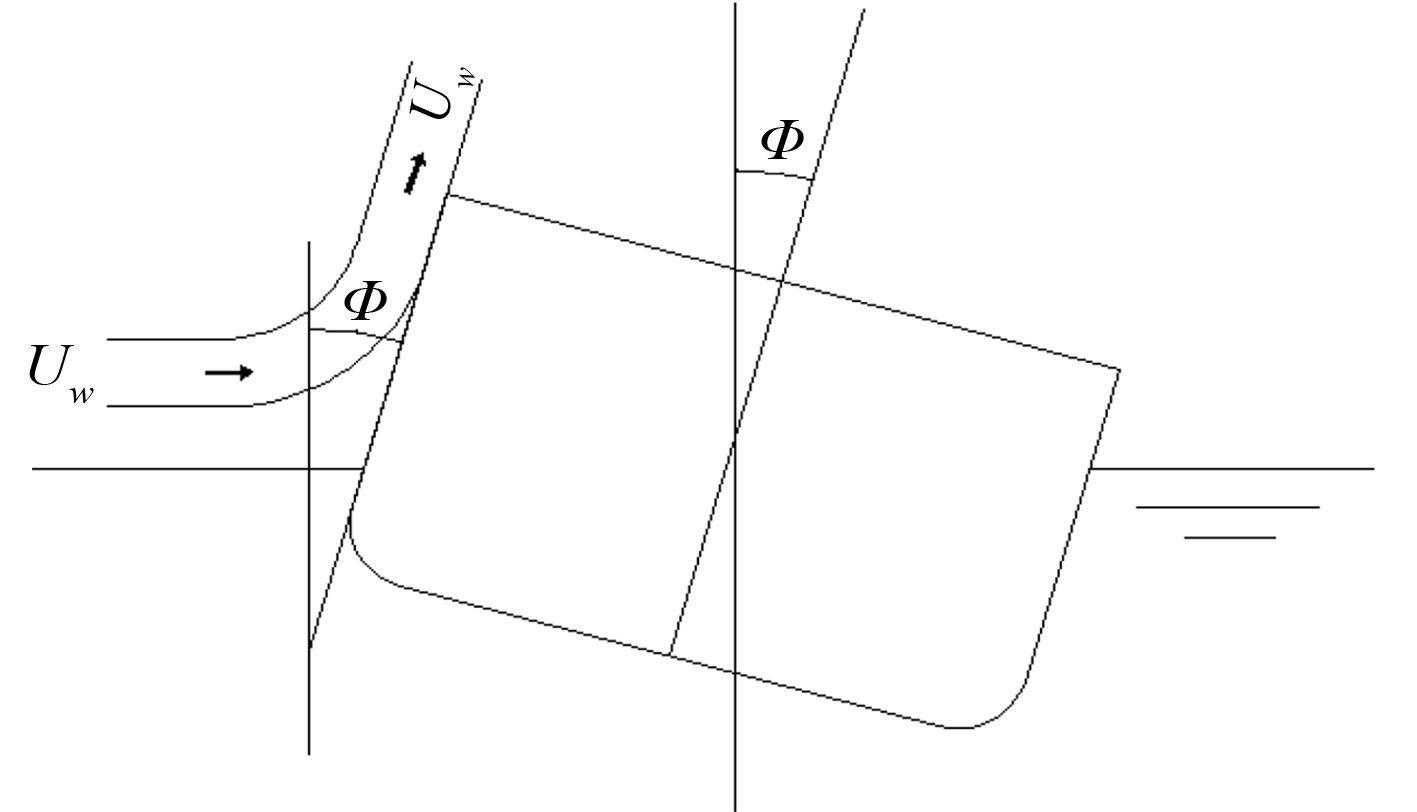
|
图 7 横风作用示意图 Fig. 7 Diagram of the transversal wind |
| $ \begin{array}{l} U(t) = \sum\limits_{i = 1}^{{N_W}} {{b_i}\sin ({\omega _{wi}}t + {\varepsilon _i})}\text{,} \\[5pt] {b_i} = \sqrt {2{S_{wind}}({\omega _{wi}})\delta \omega } \text{,}\\[5pt] {S_{wind}}({\omega _{wi}}) = 4K\frac{{U_W^2}}{\omega }\frac{{X_D^2}}{{{{(1 + X_D^2)}^{4/3}}}}\text{,}\\[5pt] \chi ({\omega _w}) = \frac{1}{{1 + {{\left( {\frac{{{\omega _w}\sqrt {{A_L}} }}{{\pi {U_W}}}} \right)}^{4/3}}}}\text{。} \end{array} $ | (27) |
计算采用下列公式:
式中:K = 0.003;
当风速为 3 m/s(实际风速 24.5 m/s)时,随机风的能量密度谱如图 8 所示。
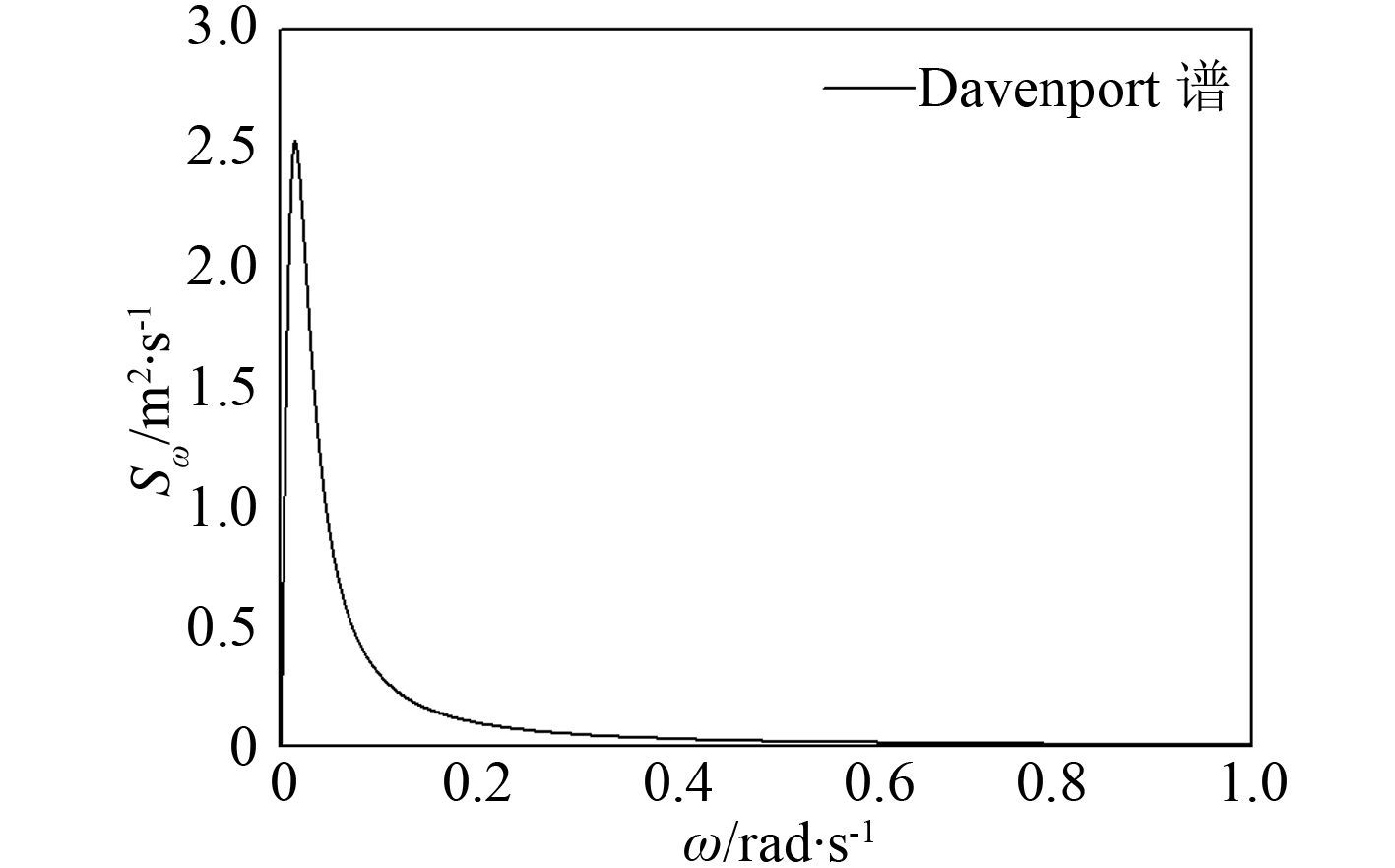
|
图 8 风速 3 m/s Davenport 风谱 Fig. 8 Davenport wind spectrum |
将风谱函数离散为 100 个频率的叠加。风的频率ωwi =(0~1 rad/s),频率间隔δωw = 0.01 rad/s。
4 计算结果 4.1 初始固定横倾为模拟货物移动导致的初始固定横倾,在式(1)的右端加上一个导致船舶初始横倾的初始力矩。
查静稳性臂曲线得到不同固定横倾对应值如表 3 所示 ,并计算横倾力矩。
|
|
表 3 不同初始横倾角对应GZ 值(模型) Tab.3 InitialGZ under different cargo shift angle(model value) |
规则波横摇运动方程:
| $ \begin{array}{l} I_{xx}'\ddot \theta + {N_1}\dot \theta + {N_3}{{\dot \theta }^3} + \Delta \cdot \sum\limits_{i = 1}^n {{C_i}{\theta ^{2i - 1}}} =\\ \quad\quad\;\;\, \Delta \cdot GM \cdot {\alpha _{m0}} \cdot \sin (\textit{Ω} t)\text{,} \end{array} $ | (28) |
| $ {\alpha _{m0}} = {K_\phi }{\alpha _0} = {K_\phi }\frac{{2\pi {\zeta _A}}}{\lambda } = {K_\phi }k{\zeta _A}\text{。} $ | (29) |
式中:αm0 为有效波倾角的幅值;Ω 为波浪频率;Kϕ 为有效波倾系数;α0 为有效波倾角;ζA 为波面抬高;λ 为波长;k 为波数。
模型在规则波中横摇运动时历如图 9 所示。统计规则波横摇计算结果和试验结果对比如 表 4所示。

|
图 9 规则波中模型试验结果与模拟对比 Fig. 9 Comparison of ship motion in regular waves between model tests and numerical results |
|
|
表 4 规则波数值模拟与试验结果对比 Tab.4 Comparison of ship motion in regular waves between model tests and numerical results |
规则波单自由横摇运用模拟结果与试验结果基本吻合,误差均小于 10%,满足不规则波横摇倾覆计算问题的精度要求。产生误差的原因主要是单自由度计算未将其他自由度运动考虑在内,相比于实际运动结果,理论结果必然存在误差。
4.3 不规则波中倾覆概率计算 4.3.1 不规则波数值模拟一般而言,随机波浪被看作是平稳随机过程,可以通过不同周期和相位的余弦波叠加得到。本文采用 ITTC 双参数谱,大部分能量集中在ωmin~ωmax 间,本文略去频率两侧总能量为 0.002 来确定波频范围。
| $ 0.002 = \frac{{\int_0^{{\omega _{\min }}} {S(\omega ){\rm d}\omega } }}{{\int_0^\infty {S(\omega ){\rm d}\omega } }} = \frac{{\int_{{\omega _{\max }}}^\infty {S(\omega ){\rm d}\omega } }}{{\int_0^\infty {S(\omega ){\rm d}\omega } }}\text{,} $ | (30) |
将频率分为 871 个规则波的叠加,波面方程为:
| $ \zeta (t) = \sum\limits_{i = 1}^N {\sqrt {2S({\omega _i})\delta \omega } } {\rm {sin}}({\omega _i}t + {\varepsilon _i})\text{。} $ | (31) |
式中:ωi 为规则波频率;δω 为分解的规则波频率间隔,取 0.01。
本文模拟模型试验有义波高 0.17 m、特征周期 2.04 s。不规则波时历数值模拟与试验测量船前波浪时历对比如图 10 所示,该种波浪情况下横摇运动时历对比如图 11 所示。不规则波三一波高统计值和横摇运动三一幅值的模拟与试验比较如表 5 所示。

|
图 10 数值模拟与试验测量波浪时历对比 Fig. 10 Comparison of irregular wave between model tests and numerical result |
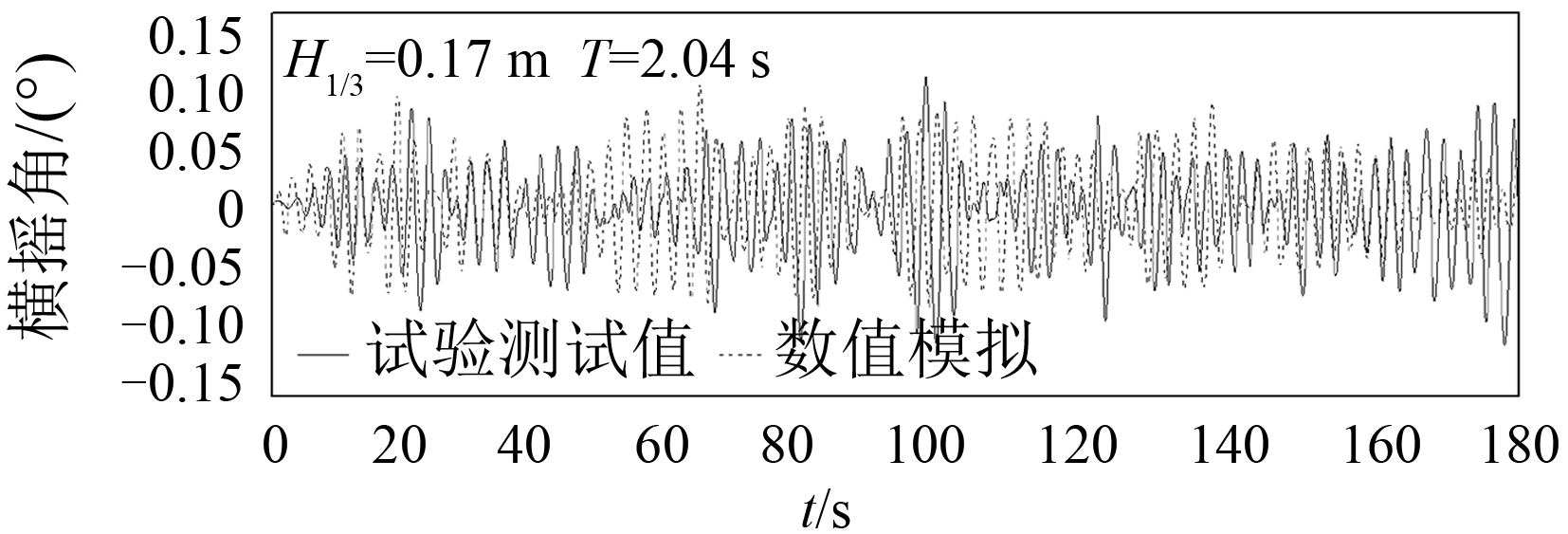
|
图 11 数值模拟与试验测量船舶横摇运动时历对比 Fig. 11 Comparison of ship rolling on the irregular wave between model tests and numerical result |
|
|
表 5 波浪和船舶横摇运动统计值验证 Tab.5 Statistics of wave amplitudes and ship motion amplitudes |
从表 5 中可看出,编制的程序在模拟不规则波和船舶横摇运动时较准确,不规则波以及运动的准确模拟是准确计算的倾覆概率的保证。
4.3.2 蒙特卡罗模拟蒙特卡罗法计算倾覆概率通过时域计算,得到足够的总样本数N,根据计算得到的倾覆次数Nc 在总样本数中的频率来计算倾覆概率的统计值P,即
| $ Pc = \frac{{Nc}}{N}\text{,} $ | (32) |
为了验证统计值的可靠行,需要计算置信区间。假定Pc 满足二项分布:
| $ P(Nc) = \frac{{N!}}{{Nc!(N - Nc)!}}{p^{Nc}}{(1 - p)^{N - Nc}}\text{,} $ | (33) |
式中p 为真实概率,当样本足够大,可认为其符合正态分布。
| $ \Delta p = \frac{2}{{\sqrt N }}\sqrt {Pc(1 - Pc)} {z_{\alpha /2}}\text{,} $ | (34) |
概率P 的置信区间可表示为:
| $ Pc - \frac{{\Delta p}}{2} \leqslant p \leqslant Pc + \frac{{\Delta p}}{2}\text{。} $ | (35) |
为使置信区间可信度为 0.95,在给定环境条件下,船舶时域样本为 1 000 次。
4.3.3 倾覆概率计算船舶实际倾覆角在统计方法被中定义为进水角、稳性消失角和 50° 的较小者,本文取倾覆角为 50°。模拟船舶在横风横浪中横摇运动暴露时间为 1 h。
本文进行了试验海况三一波高 0.17 m,特征周期 2.04 s,风速 3 m/s,改变固定横倾的倾覆概率计算,与 Kubo[2]中模型试验和数值模拟进行对比如图 12 所示。

|
图 12 船舶倾覆概率计算值和试验值对比 Fig. 12 Comparison of capsizing probability between model test and numerical result |
本文单自由度计算的结果与 Kubo 等计算的结果趋势相近,本文计算结果偏大,在货物移动导致横倾 10° 时与试验结果更加吻合。
5 结 语本文基于单自由度横摇运动模型,对瘫船风浪作用下的稳性进行了直接评估。
通过几何分析推导出船舶具有初始固定横倾时回复力臂计算方法。探讨了对于 CEHIPAR2792 标准模型大角度横摇阻尼系数的确定方法,并将数值模拟与模型自由衰减试验对比。
将风浪中横摇运动数值结果与船模的试验结果进行对比,验证了单自由度数值方法的可靠性,得到以下结论:
1)船舶在不同初始横倾下的静稳性曲线变化明显,需重新计算,本文给出了计算方法。
2)采用能量法计算船舶横摇阻尼系数能够获得良好的结果,采用一次项加三次项多项式模拟 CEHIPAR2792标准模型阻尼力矩的方法结果可靠。
3)不规则波计算中,从模拟计算时历与实验值时历图比较来看,运动幅值的误差在可接受的范围内。这种单自由度直接模拟船舶在不规则风浪中横摇运动是可行的。
4)有效波倾系数的准确取值对波浪载荷计算具有重要影响,本文采用简化模型,并使用了 SDC1/INF.6 中的有效波倾值。在未来的研究中,有条件的情况下应采用试验法测量船舶有效波倾系数,使计算结果准确。
5)当船舶具有货物移动等造成的初始横倾角时,同等海况下的倾覆概率增加。因此在实际航行中,货物绑扎的检查尤为重要,由于绑扎不牢、横摇过大等原因导致货物移动,会使船舶倾覆风险大大增加,
6)单自由度计算未将其他自由度运动(如升沉、横荡、首摇等)考虑在内,相比于实际运动结果,理论预报必然存在误差。在今后的研究中,进行多自由度耦合研究是该失效模式直接评估方法发展的必然趋势。
| [1] | IMO SDC 1/INF, 6. Vulnerability assessment for dead-ship stability failure mode[C]. Italy and Japan, 2014. |
| [2] | IMO SDC 1/INF, 8, ANNEX 16. Proposed amendments to part b of the 2008 is code to assess the Vulnerability of ships to the dead ship stability failure mode[C]. Italy and Japan, 2014. |
| [3] | KUBO T, UMEDA N, IZAWA S, et al. Total stability failure probability of a ship in irregular beam wind and waves:model experiment and numerical simulation[C]//. Proceedings of the 11th International Conference on the Stability of Ships and Oceans Vehicles, 2009:39-46. |
| [4] | 盛振邦, 刘应中. 船舶原理[M]. 上海: 上海交通大学出版社, 2003. |
| [5] | BULIAN G, FRANCESCUTTO A. A simplified modular approach for the prediction of the roll motion due to the combined action of wind and waves[J]. Proceedings of the Institution of Mechanical Engineers, Part M:Journal of Engineering for the Maritime Environment, 2004, 218 (3): 189–212. DOI: 10.1243/1475090041737958 |
| [6] | 李培勇, 冯铁城, 裘泳铭. 三体船横摇运动[J]. 中国造船, 2003, 44 (1): 24–30. |
| [7] | 汤忠谷, 韩久瑞, 施立人, 等. 海船风压试验研究[J]. 武汉水运工程学院学报, 1979 (2): 1–18. |
| [8] | DAVENPORT A G. The spectrum of horizontal gustiness near the ground in strong winds[J]. Journal of the Royal Meteorological Society, 1961, 87 : 194–211. DOI: 10.1002/(ISSN)1477-870X |
 2017, Vol. 39
2017, Vol. 39
