现代工程系统规模越来越大、系统之间的交互作用越来越精细、复杂,已很难应用传统优化方法,并通过经验来协调系统内部的耦合效应。在此背景下,MDO 技术应运而生。MDO 是 Sobieski 等[1]在研究大型结构设计优化问题时提出的一种耦合系统设计优化方法,其基本思想是通过充分探索和利用系统中相互作用的协同机制来设计复杂系统和子系统[2]。MDO 方法最先在航空航天领域获得研究和应用,已初见成效[3-6],随后迅速扩展至武器、汽车、机械、船舶等诸多领域。自 20 世纪 80 年代末以来,MDO 技术得到美国、俄罗斯、欧洲等国家政府机构、企业界和学术机构的支持和研究,MDO 作为一门正在崛起的新的工程学科,必将成为优化设计的大趋势[7]。
MDO 从理论层面解决了多系统的协同设计问题,MDO 算法则是这一理论的具体实现方法。显然,由于设计问题的不同,所要求的实现方法也就不同,从而发展了各种各具特点的 MDO 算法。这就要求设计研究人员对各不同 MDO 算法有一定的了解,为此,本文根据相关文献,对近年来发展的 MDO 算法进行总结,并重点介绍几种特殊 MDO 算法应用目的、分解方法及性能特点,为实际应用提供参考。最后,讨论了当前 MDO 算法研究中存在的问题,并提出了若干建议。
1 MDO 算法概述MDO 算法又称为 MDO 过程、MDO 体系结构(MDO Architecture),区别于传统最优化方法,MDO 算法关注优化过程的组织方式、耦合信息的传递和协同策略,而不是搜索策略本身。为便于阐述 MDO 算法原理及不同 MDO 算法的特点,首先给出 MDO 算法的一般数学表达形式,如式(1)所示,该式又被称为同时优化算法(All-at-once,AAO)[8]。
| $ \begin{array}{l} {\rm{Find: }}{\left[ {x,{y^t},y,\bar y} \right]^{{\rm{ }}{\rm T}}}{\rm{ }} \text{,}\\ {\rm{Min: }}{f_0}(x,y) + \sum\limits_i {{f_i}({x_0},{x_i},{y_i})}\text{,} \\ {\rm{ S}}{\rm{. t}}{\rm{.: }}{c_0}(x,y) \geqslant 0\text{,} \\ \;\;\;\;\;\;\;\;\;\;{c_i}(({x_0},{x_i},{y_i}) \geqslant 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1, \cdots ,N\text{;}\\ \;\;\;\;\;\;\;\;\;\;c_i^c = y_i^t - {y_i} = 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1, \cdots ,N\text{;}\\ \;\;\;\;\;\;\;\;\;\;{R_i}({x_0},{x_i},y_{j \ne i}^t,{{\bar y}_i},{y_i}) = 0\;\;\;\;\;\;i = 1, \cdots ,N\text{。} \end{array} $ | (1) |
其中:x 为设计变量,
AAO 算法对所有变量,包括设计变量、状态变量、输入/输出耦合变量,进行同时优化,问题规模大、收敛速度慢,实际应用少,但是,通过对约束条件的不同处理可得到更高效的 MDO 算法。
消除 AAO 的一致性约束后,得到同时分析和设计算法(Simulation Analysis and Design,SAND),优化问题规模明显减小,但学科分析控制方程求解依然困难;消除 SAND 中的Ri = 0 学约束可得到的多学科可行法(Multidisciplinary Discipline Feasible,MDF),该算法仅需对设计变量进行优化,每一步迭代都能够得到多学科可行解,但计算过程比较复杂,优化效率不高;消除 AAO 的Ri = 0 约束可得到单学科可行法(Individual Discipline Feasible,IDF),该算法的各子学科分析计算可并行执行,优化过程收敛能得到多学科可行解,应用梯度优化算法时,计算量大,收敛困难。
上述 4 种 MDO 算法均只有一个优化器,所有优化一次完成,称之为单级整体式 MDO 算法。这类算法结构简单,容易建模实现,但各子学科只有“分析”没有“优化”,子学科缺乏优化自主权,而实际工程系统总是希望各子学科的设计优化由学科专家来主导完成。基于这一需求,多级分布式 MDO 算法得到发展和实际应用,其最典型的结构是拥有一个系统级优化问题和多个子系统优化问题,系统层与各子系统对整个系统的设计具有不同程度的自由度,这种架构与工程设计过程相吻合。对于多级 MDO 算法,按照协同策略又可以将其分为基于 IDF 策略和 MDF 策略的多级分布式 MDO 算法两大类,前者主要通过在系统层设置关于耦合变量的一致性约束进行协同;后者则通过多学科分析来满足耦合变量的一致性。
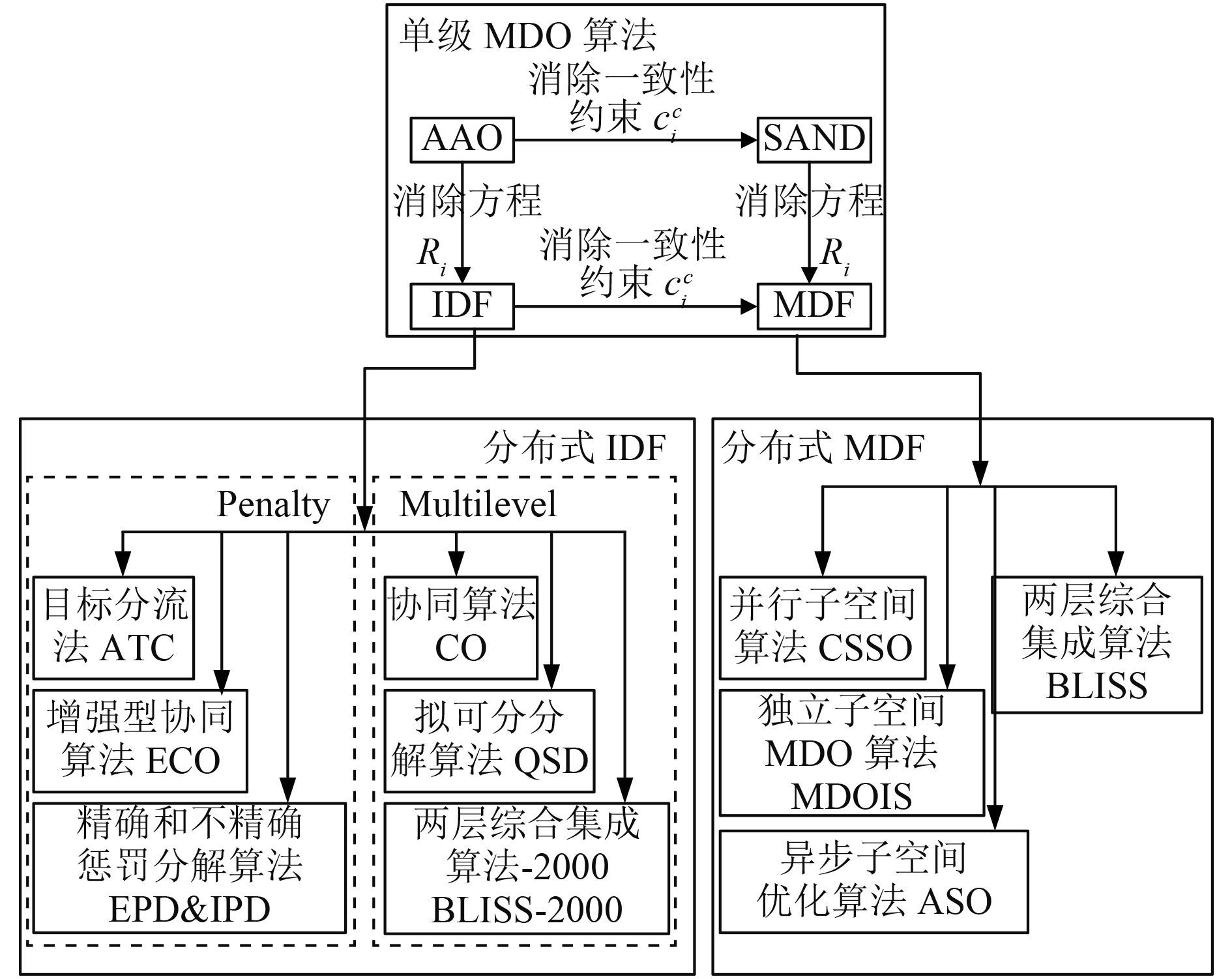
按照上述分类方法,本文对近年来发展的 MDO 算法进行归类整理,如图 1 所示。其中,单级 MDO 算法在上文已作简要介绍,文献[9-10]中也可以找到详细的阐述,本文将不再做进一步阐述;多级优化算法中,以 CO,CSSO,BLISS 的研究最多,其发展已较为成熟,本文仅对其基本原理和特性作简要介绍,重点研究几种有特殊应用要求的多级 MDO 算法基本原理和特点。
|
图 1 MDO 算法分类 Fig. 1 Classification of the MDO Architecture |
1)并行子空间算法(Concurrent Subspace Optimization,CSSO)[11-12]是最早提出的多级分布式 MDO 算法之一。其基本思想是将系统优化问题分解为若干个设计变量不相交的子优化问题,各子系统优化的目标函数均为原系统优化问题的目标函数,各子学科只对本学科局部设计变量进行优化,所需的耦合输入变量用近似模型代替。CSSO 需要进行复杂的多学科分析(Multidisciplinary Analysis,MDA),系统分解要求各子学科设计变量集不相交,在工程上较难满足,限制了该方法的实际应用。
2)协同优化算法(Collaborative Optimization,CO)是目前研究最多、应用研究最为广泛的 MDO 算法[13]。其基本思想是将系统进行层次分解,各子系统只与父系统进行数据交换,系统层目标函数为原问题目标函数,各子系统以最小化与系统分配的目标方案的差异为目标函数,系统层通过一致性约束协调各子学科进行并行优化。CO 算法,子学科优化自治性高,获得工程设计师的青睐,但其系统优化问题不满足 KKT 最优化条件,其数学收敛性尚未得到证明[14-15]。
3)增强型协同算法(Enhanced Collaborative Optimization,ECO)[16]的基本思想是将 CO 算法的系统层与子系统层目标函数对调,增强各子学科对目标函数的“影响力”。研究表明[17],ECO 比 CO 的分析次数更少,但构建及更新子学科模型需要增加额外的时间。
4)两层综合集成算法(Bilevel Integrated System Synthesis,BLISS)[18]将设计变量分为全局(系统)设计变量和学科局部设计变量,应用泰勒展开式构造原问题目标函数近似式,利用梯度指导的方法,交替优化全局设计变量和学科局部设计变量,直到获得系统最优解。这一过程需进行大量的偏导数计算,优化计算成本高,通过采用响应面方法、Kring 方法可得到缓解。
5)目标分流法(Analytical Target Cascading,ATC)[19]的基本思想是将系统设计要求,包括目标函数、约束条件,按照层次系统由上到下逐级传递到子系统,各子系统围绕系统设计要求对各学科局部设计变量进行优化,直到获得满足目标的设计方案,若无法完全满足目标值,则返回最接近目标的设计方案,ATC 与 CO 算法思想相似。目前,关于ATC算法的性能研究,目前尚不多,但已在汽车、桥梁、飞机、船舶等领域开展应用研究。
2.2 几种特殊的多级分布式 MDO 算法 2.2.1 精确和非精确惩罚分解算法若 MDO 问题中没有系统约束c0 或系统目标函数f0,可以应用 EPD 或 IPD 算法[20],其子学科i 优化问题定义如下式所示:
| $ \begin{array}{l} {\rm{Find}}:[{{\hat x}_{0i}},{x_i}]\text{,}\\ {\begin{aligned} {\rm{Min}}: & {f_i}({{\hat x}_{0i}},{x_i},{y_i}({{\hat x}_{0i}},{x_i},y_{j \ne i}^t)) +\\ & {\Phi _i}({{\hat x}_{0i}} - {x_0},y_i^t - {y_i}({{\hat x}_{0i}},{x_i},y))\text{,} \end{aligned}} \\ {\rm{S}}{\rm{.t}}{\rm{.}}:{\rm{ }}{c_i}({{\hat x}_{0i}},{x_i},{y_i}({x_{0i}},{x_i},y_{j \ne i}^t)) \geqslant 0\text{。} \end{array} $ | (2) |
其中:Φi 为关于学科i 与系统层之间不一致性的惩罚函数。在 EPD 中,Φi 为关于耦合变量的线性惩罚函数;在 IPD 中,Φi 为关于耦合变量的、带权重因子的二次非线性惩罚函数。
EPD 和 IPD 的系统优化问题相同,它是以最小化各子系统惩罚函数Φi 之和为目标的无约束优化问题,如下式所示:
| $ \begin{split} \\[-10pt] {\rm{Find}}: & [{x_0},{y^t}]\text{,}\\ {\rm{Min}}: & \sum\limits_{i = 1}^N {{\omega _i}\Phi _i^*\left( {{x_0},{y^t}} \right)} = \\ & \sum\limits_{i = 1}^N {{\omega _i}{\Phi _i}\left( {{{\hat x}_{0i}} - {x_0},y_i^t - {y_i}\left( {{{\hat x}_{0i}},{x_i},y_{j \ne i}^t} \right)} \right)} \text{。} \end{split} $ | (3) |
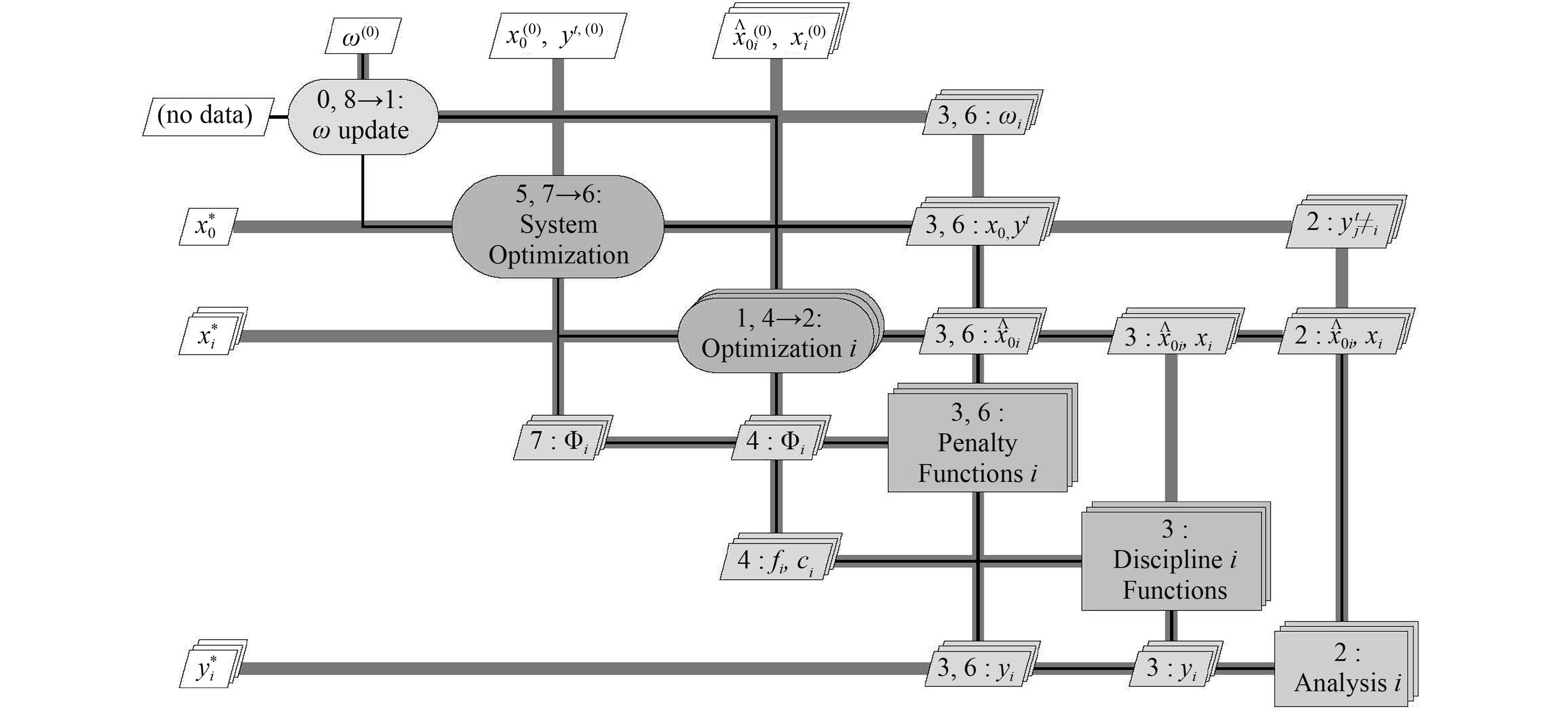
其中:ωi 为惩罚函数的权重因子,它由系统优化器进行更新,当ωi 趋于无穷大,而系统目标函数值不变(或增加量小于某给定小数)时,则表示优化过程收敛。DeMiguel 等[21]在数学上已证明了 IPD 和 EPD 的收敛性,其研究也表明,IPD 和 EPD 的计算量随共享耦合变量的增加而增加。
|
图 2 EPD&IPD算法结构图 Fig. 2 Diagram of the EPD&IPD Architecture |
若 MDO 问题没有系统约束c0 或系统目标f0,同时不存在共享设计变量x0,则可以采用独立子空间 MDO 算法(MDO of Independent Subspace,MDOIS)[22]。这种情况下,各学科之间只存在输入、输出耦合,各学科优化问题可完全分离,学科i 优化问题可定义如下:
| $ \begin{array}{l} {\rm{Find:}}[{x_i}]\text{,}\\ {\rm{Min: }}{f_i}\left( {{x_i},{y_i}\left( {{x_i},y_{j \ne i}^t} \right)} \right)\text{,}\\ {\rm{ S}}{\rm{.t}}{\rm{. : }}{c_i}\left( {{x_i},{y_i}\left( {{x_i},y_{j \ne i}^t} \right)} \right) \geqslant 0\text{。} \end{array} $ | (4) |
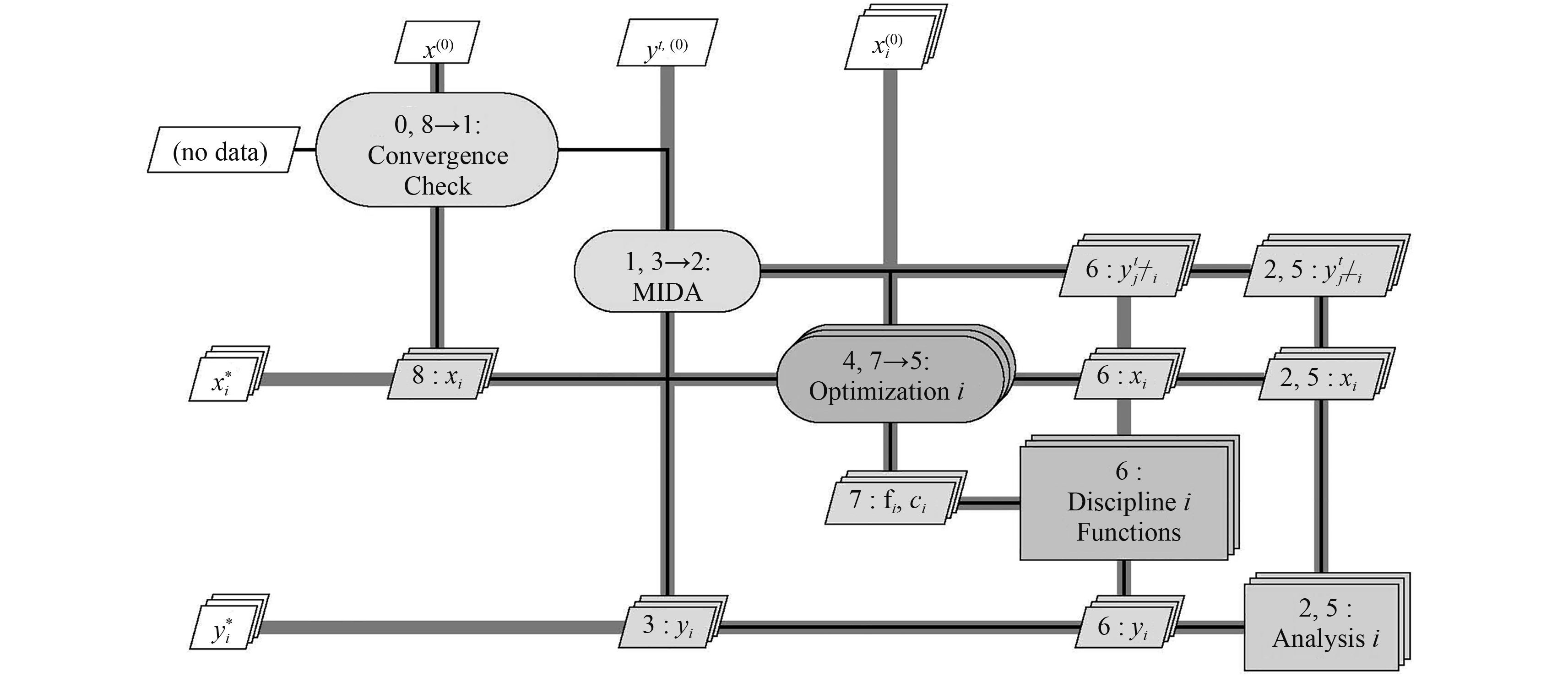
MDOIS 的最大特点是,不存在系统优化问题。如图 3 所示,它是通过 MDA 过程来引导各学科设计优化过程,当 MDA 过程收敛时,即获得系统最优解,它属于分布式 MDF 算法。研究表明,在满足假定条件的前提下,MDOIS 均能获得最优解[23];基准试验研究发现,在很多数情况下,获得同样的最优解,MDOIS 比 MDF 过程所需的分析次数还要少,但在应用的灵活性上却不及后者[24]。
|
图 3 MDOIS 算法结构图 Fig. 3 Diagram of the MDOIS Architecture |
若在 MDO 过程中,不同学科进行分析计算时所耗时间相差很大时,例如,在进行飞机机翼构型优化时,涉及空气动力学分析、结构力学分析,前者分析所需时间通常要比后者高一个数量级,为减少总的优化时间,可应用异步子空间法(Asymmetric Subspace Optimization, ASO)[25]。为了减少高精度分析计算的次数,用基于低精度分析方法的优化模块替换原分析计算模块直接进行优化;而需要进行高精度分析的学科则由系统层进行优化,其系统及子系统优化问题定义如式(5)和式(6)所示,其中,k 表示需要进行高精度分析的学科。
| $ \begin{array}{l} {\rm{Find}}:[{x_0},{x_k}]\text{,}\\ {\rm{Min}}:{f_0}(x,y(x,y)){\rm{ }} + \sum\limits_k {{f_k}({x_0},{x_k},{y_k}({x_0},{x_k},{y_{j \ne k}}))} \text{,}\\ {\rm{S}}{\rm{.t}}{\rm{.}}:{c_0}(x,y(x,y)) \geqslant 0\text{,}\\ {\rm{ }}{c_k}({x_0},{x_k},{y_k}({x_0},{x_k},{y_{j \ne k}})) \geqslant 0{\rm{ for all }}k\text{。} \end{array} $ | (5) |
| $ \begin{array}{l} {\rm{Find}}:\left[ {{x_i}} \right]\text{,}\\ {\rm{Min}}:{f_0}(x,y(x,y)) + {f_i}({x_0},{x_i},{y_i}({x_0},{x_i},{y_{j \ne i}}))\text{,}\\ {\rm{S}}{\rm{.t}}{\rm{.}}:{c_i}({x_0},{x_i},{y_i}({x_0},{x_i},{y_{j \ne i}})) \geqslant 0{\rm{ }}\text{。} \end{array} $ | (6) |
ASO 算法属于分布式 MDF 算法,有复杂的 MDA 过程,相应的,需要进行系统灵敏度计算,可应用耦合优化后灵敏度方程来计算[26],也可应用耦合伴随方程[27]计算。飞机机翼的 MDO 应用研究表明,应用 ASO 算法不仅大幅减少了空气动力学分析计算的次数,甚至一定程度上还减少了结构分析计算的次数;2 个学科分析计算耗时差距越大,总的分析计算次数减少越明显,ASO 过程的分析次数也越接近 MDF 过程。也即是说,只有当 2 个学科分析计算时间相差很大时,ASO 算法才具有优势。
3 结 语本文对近年来 MDO 算法研究成果进行较为系统的归纳总结,对主要 MDO 算法,特别是一些新的、有特殊应用环境的 MDO 算法进行重点介绍,对其特点及性能特点进行了分析评述,可为 MDO 算法的工程应用研究及创新 MDO 算法发展提供支撑和导向。
MDO 算法研究已经取得了丰硕的成果,为工程应用提供了更多的选择,但同时又带来新的挑战:即面对给定的 MDO 问题,选择哪一种 MDO 算法,建模更快捷、优化效率更高、优化质量更好,也就是说,需要了解不同 MDO 算法对于特定问题的解决能力。然而,由于不同研究人员实现同一算法的方式、计算环境、测试算例存在差异,特别是研究人员对算法的熟悉程度或偏好不同,都容易引起评估结果出现偏差,甚至相互矛盾。为客观起见,应尽可能在一套规范的方法和流程下,对不同 MDO 算法进行对比研究,从而准确把握不同 MDO 算法的应用要求和性能特点,这类似于船舶水动力性能试验研究中的标模基准试验研究,本文称之为“MDO 算法基准试验研究”,国内外在该领域已开展了一些研究[28-32],但在以下 2 个方面还需做进一步的深入研究:
1)基准测试算例简单,不利于评估 MDO 算法在处理大规模工程问题时的性能。目前发展的基准测试算例大多为简化后的工程设计模型,维度低、分析模型简单、计算复杂度低,而实际工程系统设计变量、约束模型可能达到 103 量级,一次学科分析可能需要花费几小时甚至几十小时,这些分析计算还可能是由不同的计算机采用不同的程序或软件完成,而 MDO 算法表现的性能又与问题规模密切相关[33]。因此,应进一步开展具有大工程系统特征的基准测试算例研究。
2)MDO 基准试验研究针对的对象过于集中,不利于新算法的推广应用。从发表的文献来看,目前的 MDO 基准试验比较研究大多是针对 MDF,IDF,CO,CSSO 等少数几种发展时间较长、已较成熟的算法,而对 ASO,MDOIS 等新算法的对比研究凤毛麟角,不利于新算法的推广应用。
另外,面向复杂大系统的 MDO 算法应用及新算法开发研究将是今后 MDO 算法研究的重要方向。当设计系统的规模大到一定程度时,MDO 算法建模的复杂性、收敛性、稳定性等性能可能发生根本性的改变,因此,今后的 MDO 算法研究应更紧密地结合实际工程大系统,而不是仅局限于一些数学算例或工程概念设计阶段的简单问题。
| [1] | SOBIESZCZANSKI-SOBIESKI.J. A linear decomposition method for large optimization problems-blueprint for development[R]. NASA Technical Memorandum 83248, Feb. 1982. |
| [2] | GIESING HOSEPH P, BARTHELEMY J M. A summary of industry MDO application and needs[C]//An AIAA White Paper, 7th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, 1998. |
| [3] | OLDS, JOHN R. Multidisciplinary design techniques applied to conceptual aerospace vehicle desig[D]. North Carolina State University, 1993. |
| [4] | GIUNTA A A, GOLIVIDOV O, KNILL D L, et al. Multidisciplinry design optimization of advanced aircraft configurations[R]. MAD Center Report 96-06-01. |
| [5] | JOEL M G. Multidisciplinary design optimization of a strut-braced wing aircraft[M]. Virginia Polytechnic Institute and State University, April 13, 1998. |
| [6] | 蔡伟. 不确定性多目标MDO理论及其在飞行器总体设计中的应用研究[D]. 长沙:国防科学技术大学, 2008. http://cdmd.cnki.com.cn/Article/CDMD-90002-2009213878.htm |
| [7] | SRINIVAS K, SOBIESZCZANSKI-SOBIESKI J. Multidisciplinary design optimization-some formal methods, framework requirement, and application to vehicle design[C]//Int.J.VehicleDesign(Special Issue), 3-22. |
| [8] | CRAMER E J, DENNIS Jr J E, FRANK P D, et al. Problem formulation for multidisciplinary optimization[J]. SIAM Journal on Optimization, 1994, 4 (4): 754–776. DOI: 10.1137/0804044 |
| [9] | HAFTKA R T. Simultaneous analysis and design[J]. AIAA Journal, 1985, 7 (7): 1099–1103. |
| [10] | BALLING R J, SOBIESZCZANSKI-SOBIESKI J. Optimization of coupled systems:a critical overview of approaches[J]. AIAA Journal, 1996, 34 (1): 6–17. DOI: 10.2514/3.13015 |
| [11] | SELLAR R S, BATILL S M, RENAUD J E. Response surface based, concurrent subspace optimization for multidisciplinary system design[C]//34th AIAA Aerospace Sciences and Meeting Exhibit, 1996. |
| [12] | RENAUD, JOHN E. Sequential approximation in non-hierarchic system decomposition and optimization:a multidisciplinary design tool[D]. Rensselaer Polytechnic Institute, 1992. |
| [13] | KROO J, ALTUS S, SOBIESZCZANSKI-SOBIESKI J, et al. Multidisciplinary optimization methods for aircraft preliminary design[J], AIAA-94-4325, 1994. |
| [14] | ALEXANDROV N M, LEWIS R M. Analytical and computational aspects of collaborative optimization for multidisciplinary design[J]. AIAA Journal, 2002, 40 (2): 301–309. DOI: 10.2514/2.1646 |
| [15] | DEMIGUEL A V, MURRAY W. An analysis of collaborative optimization methods[C]//8th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis &Optimization, Long Beach, CA, 2000. |
| [16] | BRIAN R, ILANKROO. Enhanced collaborative optimization:application to an analytic test problem and aircraft design[C]//In 12th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, number September, Victoria, British Columbia, Canada, September 2008. |
| [17] | BRIAN D R. Aircraft family design using enhanced collaborative optimization[D]. Stanford University, 2008. |
| [18] | JAROSLAW, SOBESZCZANSKI-SOBIESKI. Bi-level integrated system synthesis(BLISS)[J]. NASA/TM-1998-208715; |
| [19] | KIM H M, MICHELENA N F, PAPALAMBROS P Y, et al. Target cascading in optimal system design[J]. Journal of Mechanical Design, 2003, 125 (3): 474–480. DOI: 10.1115/1.1582501 |
| [20] | ANGEL-VICTOR D. Two decomposition algorithms for nonconvex optimization problems with global variables[D]. Stanford University, 2001. |
| [21] | DEMIGUEL V, MURRAY W. A local convergence analysis of bileveldecomposition algorithms[J]. Optimization and Engineering, 2006, 7 (2): 99–133. DOI: 10.1007/s11081-006-6835-3 |
| [22] | MOON-KYUN S, GYUNG-JIN P. Multidisciplinary design optimization based on independent subspaces[J]. International Journal for Numerical Methods in Engineering, 2005 (64): 599–617. |
| [23] | SI Yi, SHIN J K, PARK G J. Comparison of MDO methods with mathematical examples[J]. Structural and Multidisciplinary Optimization, 2008 (39): 391–402. |
| [24] | IAN R .Chittick, Joaquim R. R. A.Martins. An asymmetric suboptimization approach to aerostructural optimization[J]. Optimization and Engineering, 2009, 10 (1): 133–152. DOI: 10.1007/s11081-008-9046-2 |
| [25] | MARTINS J R R A, ALONSO J J, REUTHER J J. A coupled-adjoint sensitivity analysis method for high-fidelity aero-structural design[J]. Optimization and Engineering, 2005, 6 (1): 33–62. DOI: 10.1023/B:OPTE.0000048536.47956.62 |
| [26] | SRINIVAS KODIYALAM. Evaluation of methods for multidisciplinary design optimization(MDO), PhaseⅠ[C]//NASA/CR-1998-20876. |
| [27] | SRINIVAS KODIYALAM, CHARLES YUAN. Evaluation of methods for multidisciplinary design optimization(MDO), Phase Ⅱ[C]//NASA/CR-2000-210313. |
| [28] | 赵敏, 操安喜, 崔维成. 多学科设计优化方法的比较[J]. 中国造船, 2008, 49 (3): 68–78. |
| [29] | 孔凡国, 李钰. 多学科设计优化方法与传统设计优化方法的比较研究[J]. 计算机工程与科学, 2008, 30 (7): 136–138. |
| [30] | HULME K F, BOLEBAUM C L. A comparison of solution strategies for simulation-based multidisciplinary design optimization[C]//AIAA-98-4977; |
| [31] | 龚春林, 谷良贤, 袁建平. 基于全局优化算法的多学科优化计算构架[J]. 西北工业大学学报, 2009, 27 (1): 52–56. |
| [32] | 李世海. 多学科设计优化(MDO)算法研究[D]. 中国地质大学(北京)硕士学位论文, 2009. http://cdmd.cnki.com.cn/Article/CDMD-11415-2009076095.htm |
| [33] | Nathan P. Tedford, Joaquim R.R.A.Martins. Benchmarking multidisciplinary design optimization algorithms[J]. Optim Eng, 2010 (11): 159–183. |
 2017, Vol. 39
2017, Vol. 39
