0 引言

对水域的径流预测一直都是船舶航运安全管理中的重要环节，预测的准确程度受到多种不确定性因素的影响，而目前国际上通用的预测方法都基于相关向量回归模型，该模型的准确性与其中的不确定变化量具有非线性的关系^[1-2]。本文首先建立径流的自回归分析模型，然后建立了相对稳定的非线性矩阵，对径流的变量关系进行预测，并基于历史数据对该模型的预测准确度进行仿真。

1 径流向量自回归模型的建立

下面建立径流的多变量随机模型。首先确定一般的相关向量平稳函数：

${Y_t}=({Y_{1t}}, {Y_{2t}}, \cdots, {Y_{mt}})'{\rm{ }}t=0, \pm 1, \pm 2, \cdots \cdots。$

其中${Y_t}$协差矩阵为：

$ \boldsymbol \varGamma(k)={\mathop{\rm cov}}({Y_t}, {Y_{t - k}})=E[({Y_t}-\mu)({Y_{t-k}}-\mu)']。 $

(2)

与k相关。设矩阵

$ \boldsymbol\varGamma(k)={\left({\begin{array}{*{20}{c}} {{\gamma _{11}}}&{{\gamma _{12}}}&\cdots &{{\gamma _{1m}}}\\ {{\gamma _{21}}}&{{\gamma _{22}}}&\cdots &{{\gamma _{2m}}}\\ \vdots &\vdots &\vdots &\vdots \\ {{\gamma _{m1}}}&{{\gamma _{m2}}}&\cdots &{{\gamma _{mm}}} \end{array}} \right)_k}。 $

(3)

得到相关序列$\{ \Gamma(k)\} $，满足

$ {\gamma _{ij}}(k)={\gamma _{ji}}(- k)\;\Gamma(k)=\Gamma '(- k)。 $

(4)

设$\varOmega=\sum\limits_{k=- \infty }^{+\infty } {\Gamma(k)} $，则$\varOmega=\Gamma(0)+\sum\limits_{k=1}^\infty {[\Gamma(k)}+\Gamma(k)']$。上式为${Y_t}$的协差矩阵。${Y_t}$的输出谱函数为：

$ \begin{array}{l} {f_{{Y_t}}}(\omega)=\frac{1}{{2{\rm{\pi }} }}\sum\limits_{k=- \infty }^{+\infty } {\Gamma(k)} {e^{ - i\omega k}}=\\[14pt] \;\;\;\;\;\;\;\;\;\;\frac{1}{{2{\rm{\pi }} }}\{ {\Gamma _0}+\sum\limits_{k=1}^\infty {[\Gamma(k)} {e^{-i\omega k}}+\Gamma(k)'{e^{i\omega k}}]\}。\end{array} $

(5)

则$\hat {\boldsymbol\varGamma}(k)=\frac{1}{T}\sum\limits_{t=k+1}^T {({Y_t} - \bar Y)}({Y_{t - k}} - \bar Y)', {\rm{ }}k=0, 1, 2, \cdots $为$\boldsymbol\varGamma(k)$的估计式，满足当$M \to \infty, \frac{M}{T} \to 0$。

设

$ \hat \varOmega=\hat \Gamma(0)+\sum\limits_{k=1}^M {(1 - \frac{k}{{M+1}})[\hat \Gamma(k)}+\hat \Gamma '(k)]， $

(6)

为Ω的一致估计式。

设径流的估计式为单稳定的过程，则其中应加入干扰的白噪声过程WN向量。对两者建立统一的线性过程函数，从而能够增强预测的准确程度^[3-4]。共有4种过程，其预测向量的实现过程如下：

1）$VAR(1)$过程，回归模型为${Y_t}=\phi {Y_{t - 1}}+{\varepsilon _t}$。其中$\boldsymbol\phi $为$m \times m$矩阵，${\boldsymbol\varepsilon _t}$为向量WN。由于是线性关系，因此模型的平稳性$\phi $特征值小于1。

2）VMA(1)过程，回归模型为${Y_t}={\varepsilon _t}+\theta {\varepsilon _{t - 1}}$。其中$ \boldsymbol\theta $为$m \times m$矩阵，${ \boldsymbol\varepsilon _t}$为向量WN 。为满足可逆性要求，$ \boldsymbol\theta $的特征值小于1。因此，$VMA(1)$过程绝对平稳。

3）$VARMA(p, q)$过程，回归模型为

$ {Y_t}={\phi _1}{Y_{t - 1}}+\cdots+{\phi _p}{Y_{t - p}}+{\varepsilon _t}+{\theta _1}{\varepsilon _{t - 1}}+\cdots+{\theta _q}{\varepsilon _{t - q}}。 $

(7)

式中，${\boldsymbol\phi _i}$和${\boldsymbol\theta _j}$均为$m \times m$矩阵。为满足平稳性要求，要求$\det(I - {\phi _1}Z - \cdots - {\phi _p}{Z^p})=0$复根的模必大于1，则模型可逆。

4）$VMA(\infty)$过程，回归函数为

$ {Y_t}=\mu+{\varepsilon _t}+\sum\limits_{j=1}^\infty {{\theta _j}{\varepsilon _{t - j}}} \;{\varepsilon _t} \sim WN(0, \Omega)\;E{Y_t}=\mu。 $

(8)

计算得到${Y_t}$的协差矩阵为

$ \boldsymbol\varGamma(k)=\sum\limits_{j=0}^\infty {{\theta _{j+k}}} \Omega {\theta _j}, {\rm{ }}k=0, 1, 2, \cdots。 $

(9)

因此，$VMA(\infty)$的过程平稳。

2 不确定性的预测分析 2.1 冲击函数

下面对VMA过程建立冲击函数

$ {Y_t}={\varepsilon _t}+\sum\limits_{j=1}^\infty {{\theta _j}{\varepsilon _{t - j}}}, {\varepsilon _t} \sim WN(0, \varOmega)。 $

(10)

由于${Y_t}$为单变量函数，因此在冲击响应函数中$\frac{{\partial {Y_{t+s}}}}{{\partial {\varepsilon _t}}}={\theta _s}$，表示${\varepsilon _t}$在t时刻每增加一个时间单位，然后经过s个时间单位后的${Y_t}$变化情况。由于${Y_t}$为向量实现过程中的唯一冲击函数，因此冲击响应$\frac{{\partial {Y_{t+s}}}}{{\partial {\varepsilon _t}}}={\boldsymbol\theta _s}$为$m \times m$矩阵。在此矩阵中，元素${\theta _{kl}}$为${\varepsilon _t}$的第l个冲击分量对${Y_{t+s}}$的影响大小。

2.2 不确定量的空间表示

下面对上述相关向量回归模型中的随机过程建立不确定状态空间^[5-6]。因此，对状态空间的模型进行确定。

设系统中${Z_t}$表示状态量，${{{Y}}_{{t}}}$表示可观测量，满足：

$ \begin{array}{l} {Z_{t+1}}={F_t}{Z_t}+{u_t}\;\;{\mu _t} \sim WN(0, {\varOmega _\mu })，\\ {Y_t}={H_t}{Z_t}+{v_t}\;\;{v_t} \sim WN(0, {\varOmega _\nu })，\end{array} $

(11)

式中，${F_t}$和${H_t}$是非随机产生的，且当F_t =F，H_t =H时，其与时间无关联，并且对任意的t都成立。所以应采用合适的非随机初始量。

2.3 径流状态的卡尔曼滤波处理

通过卡尔曼滤波算法对径流状态的变量进行过滤处理，首先以${Z_0}$为起点，分别计算${Y_1}, \cdots, {Y_T}$的状态估计量${Z_1}, \cdots, {Z_T}$，得到

$\begin{array}{l}\! {Z_{t+1\left| t \right.}}={{E(}}{Z_{t+1}}{\rm{|}}{I_t}{\rm{), }}{Y_{t+1\left| t \right.}}={{E(}}{{\rm{Y}}_{t+1}}{\rm{|}}{I_t}{\rm{)}}，\\ \!\! {\varOmega _z}(t \!+\! 1\left| t \right.)\!=\! Var{\rm{(}}{{\rm{Z}}_{t+1}}{\rm{|}}{I_t}{\rm{)}}\;{\varOmega _y}(t+1\left| t \right.)\!=\! Var{\rm{(}}{{\rm{Y}}_{t+1}}{\rm{|}}{I_t}{\rm{)}}。\end{array}$

因此，在${I_t}$条件下，可以得到在$t+1$时刻状态Z与Y的预测方差值。

$ {Z_{t\left| t \right.}}={{E(}}{Z_t}{\rm{|}}{I_t}{\rm{)}}\;{\varOmega _z}(t\left| t \right.)=Var{\rm{(}}{{\rm{Z}}_t}{\rm{|}}{I_t}{\rm{)}}\;t=1, \cdots, T。 $

(13)

式（13）为在${I_t}$状态下的Z的更新方差。

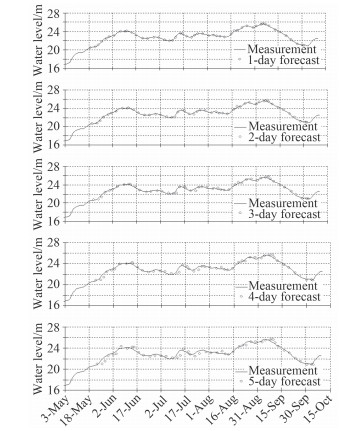
图 1为某河流的5天洪水径流预测值与实测值。该预测算法采用了本文提出的相关向量回归模型，从第一天的预测曲线可以看出，其与实测值的不确定误差很小。随着天数的增多，该河流的径流预测值与实测值不确定性误差渐渐扩大，5天的量化不确定误差值分别为0.04 m，0.07 m，0.13 m，0.19 m和0.30 m。

3 结语

本文对船舶航道的径流模型进行研究，设计了基于相关向量回归模型的预测算法，从冲击响应的仿真来看，此预测算法的误差控制在非常小的范围内，应用效果良好。