0 引言

在现代化的航运事业中，随着航道越来越拥挤，而船舶的体积、吨位越来越大，为了保证航行的安全，船舶的航速往往较低，这导致了航运成本的提升。一旦发生交通事故，往往会导致严重的经济损失，甚至造成大范围的航道停运，危害了海洋环境^[1-2]。因此，本文为了实现对船舶航行的有效预测，设计采用了混沌理论对船舶的交通安全事故进行预测分类，并通过建立合适的空间预测模型，对此算法的预测性能进行更深一步的仿真，结果表明误差处于合理的范围之内。

1 船舶时空距离数学模型

在确定船舶时空关系之前，由G-P算法得到两者的关联维度为d，并得到嵌入维数为m，需满足（m≥2d+1），接着可以得到时空维度的平均时间为τ_ω，通过公式τ_ω=（m-1）τ，得到具体的时间延迟为τ。因此，可以根据系统的时间序列$\{ x({t_i}), i=1, 2, \cdots, N\} $对m维相空间进行重新构建为：

$ \begin{array}{l} {Y_i}(t)=(x({t_i}), x({t_i}+\tau), \cdots, x({t_i}+(m - 1)\tau))，\\ i=1, 2, \cdots, M, \;\;\;M=N -(m - 1)\tau。\end{array} $

(1)

式中：Y_M为空间预报的中心点，Y_M为相空间，其邻近点Y_k通过如下方式确定：首先根据一定的算法计算出最大的指数，然后假设空间的一个点Y_M-1与Y_（M-1）a相似度最高，Y_M-1与Y_（M-1）a的空间距离表示为L_M-1，经过一定时间的进化，Y_M-1变成为Y_M，Y_（M-1）a变成为Y_（M-1）a+1，L_M-1变成为L′_M。经过上述的变化后，由Y_M接近点Y_Ma去判断出两者的距离：若基准点的相当距离L_M达到最小，此时的L’_M与L_M夹角θ也达到最小。则L_M满足：

$ {L_M}=\mathop {\min }\limits_j \left\| {{Y_M} - {Y_j}} \right\|=\left\| {{Y_M} - {Y_{Ma}}} \right\|， $

(2)

其中，$\left\| {{Y_M} - {Y_{M+1}}} \right\|=\left\| {{Y_{Ma}} - {Y_{Ma+1}}} \right\|{e^{{\lambda _1}}}$。

然后计算Y_M+1时，需要知道分量x（t_n+1）的大小，而x（t_n+1）是已知的。

假设在系统的相空间中两点的平均距离为

$ \overline L=\frac{1}{{{{(N - m+1)}^2}}}\sum\limits_{i, j=1}^{N - m+1} {\left\| {{Y_i} - {Y_j}} \right\|}， $

(3)

与Y_M-1的最近距离为

$ {\rm{\{ }}{L_{(M - 1)zj}}=\mathop {\min }\limits_j \left\{ {\left\| {{Y_{M - 1}} - {Y_j}} \right\|} \right\}， $

(4)

式中，$\left\| \bullet \right\|$表示欧氏模大小。两者的差值为：

$ \Delta L=\overline L - {L_{(M - 1){zj}}}， $

(5)

对空间设置搜索上界：

$ {\varepsilon _0}={L_{(M - 1){zj}}}+\beta \Delta L， $

(6)

下界：

$ {\varepsilon _n}={\varepsilon _0}+n\beta \Delta L， $

(7)

式中：β为分离系数大小；n为系统的放大级数，n=1，2，…。

下面对Y_k的求解进行阐述：

若系统满足

$ \{ {Y_j}|{\varepsilon _0} <\left\| {{Y_M} - {Y_j}} \right\| \leqslant {\varepsilon _n}, j=1, 2, \cdots, N - m+1\}， $

(8)

其中j至少应为2，设$Y_{Ma}^i$，i=1，2，…，令n=n+1；在对空间进行定位的过程中，坐标点的范围应满足：

$ \left| {j - M} \right| >P， $

(9)

其中P为搜索的平均周期。

当空间向量$Y_{Ma}^i - {Y_M}$与${Y_{(M - 1)a+1}} - {Y_M}$的夹角小于45°时，可以计算得到cosθ_i，i=1，2，…，令$Y_{Ma}^i$为Y_Ma：

$ \cos {\theta _i}=\frac{{(Y_{Ma}^i - {Y_M})\bullet({Y_{(M - 1)a+1}} - {Y_M})}}{{\left\| {Y_{Ma}^i - {Y_M}} \right\| \times \left\| {{Y_{(M - 1)a+1}} - {Y_M}} \right\|}}。 $

(10)

下一次循环时，令n=n+1。

重复以上步骤Y_Ma，最终得到：${L_M}=\left\| {{Y_M} - {Y_{Ma}}} \right\|$。

2 交通事故的混沌预测算法 2.1 采样周期设置

在交通事故预测时，需要设置检测系统的采样周期，越短的采样周期越有利于提高系统的灵敏度。但是这会导致噪声信号的增加。因此，在对空间中的距离进行预测时，需要尽可能选取适当的采样时间周期，从而降低发生事故的概率^[3-4]。

2.2 空间预测重构

在确定系统的相空间位置时，需要对嵌入维数m，进行混沌预测，从而能够显著降低预测位置导致的误差^[5-6]。

通过混沌信息提取，可以得到延迟时间τ的大小，然后根据时间和空间位置的相对关系，进一步确定输入维数的大小，从而减少了重构过程中的时间延迟。

设计本系统的重构相空间为：

$ X\!=\!\left[\begin{array}{l} x(1)x(2)..........x(l)\\ x(1+\tau)x(2+\tau)..........x(l+\tau)\\..\\..\\ x(1\!+\!(m\!-\!1)\tau)x(2\!+\!(m\!-\!1)\tau)..........x(l\!+\!(m\!-\!1)\tau)\end{array} \right]， $

(11)

式中， $\left[{x(1), x(2), .........x(l+(m-1)\tau)} \right]$ 为船舶交通事故预测的时间序列，l表示相空间坐标的分布。在仿真时，采用如下的采样周期信号：

$ \begin{array}{l} x(t)=5 \times(0.7 \times \sin(2\pi \times 50 \times t)+\\ \;\;\;\;\;\;\;\;\;\sin(2{\rm{\pi }} \times 100 \times t))，\end{array} $

(12)

对预测信号的混沌量设计为：

$ \begin{array}{l} y(t)=4 \times(1 - y(t - 1))\times y(t - 1)，\\ y(0)=0.41，\end{array} $

(13)

混合量为：

$ s(t)=x(t)+y(t)， $

(14)

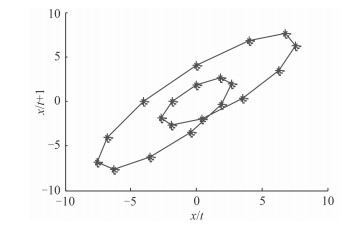
系统的预测空间维度为2，获得的相图如图 1所示。

为了增强预测精度，设计如下的优化算法：

$ \begin{array}{l} {E_{mse}}=\sqrt {\frac{1}{n}\sum\limits_{i=1}^n {{{\left({\frac{{{L_i} - {L_i}'}}{{{L_i}}}} \right)}^2}} } \times 100\%，\\ {E_{mape}}=\frac{1}{n}\sum\limits_{i=1}^n {\left| {\frac{{{L_i} - {L_i}'}}{{{L_i}}}} \right|} \times 100\%，\\ {E_{ape}}=\left| {\frac{{{L_i} - {L_i}'}}{{{L_i}}}} \right| \times 100\%。\end{array} $

(15)

式中：E_mse为均方根误差；E_mape为系统的平均误差；E_ape为绝对百分比的误差；L_i和L’_i分别为船舶交通系统的实际轨迹和预测轨迹。

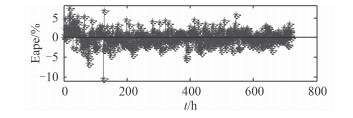
通过上述算法进行优化后，得到了如图 2所示的预测误差分布图，可以发现整个交通事故预测系统的误差范围被控制在5%的范围之内。

3 结语

船舶的交通航行预测对航运业的发展至关重要，本文提出的混沌预测算法，解决了预测过程中遇到的误差过大，稳定程度较低的问题，应用前景广泛。