0 引言

船舶齿轮箱是船舶传动系统的重要组成部分，若其发生故障会导致船舶不能运行，因此研究机械旋转故障非常重要。从以往的研究结果可以看出，从机械旋转振动信号的时域、频域等方面获取能够反映机械旋转的运动情况，从而有效的辨识机械旋转的故障情况。由于获取的信号量大，得到的特征值维数较高，在处理的过程中就会面临着降维的问题。

1 等距离映射算法

等距离映射算法是一种流形学习降维方法，其实现过程是：高维数据会在观测空间中形成一个流形，然后找出其中的主要变量，最后实现了数据的降维。

令X，Y是空间的拓扑结构，f：X→Y是连续映射，在f存在映射的情况下，若逆映射也连续，则说明X和Y同胚，那么f是同胚映射。对于空间M是流形的定义为：对于N维空间M中的任何一个点都有一个邻域U∈M，使得此邻域为N维欧氏空间的同胚映射^[1]。

在欧氏空间R^d中存在d维的域Y，f：Y→R^N是光滑嵌入，且N > d。随机生成数据$\{ {y_i}\} \subset Y$，那么在经过f映射后得到数据空间$\{ {x_i}=f({y_i})\} \subset {R^N}$，则Y是隐空间，{y_i}是隐数据。

等距离映射法是在多维尺度分析和邻域图的基础上发展起来的全局非线性流形学习方法。其实现过程为：

1）建立邻域图G：计算观测数据集X中数据x_i，i=1，2，…，n，x_i∈R^D，中任意2点的欧氏距离d_E（x_i，x_j），根据k近邻定理，得到x_i的邻域点$x_i^1,x_i^2,...,x_i^k$，即为N_i。从而将采样点邻域拓扑结构G表示为，节点是采样点，边是欧氏距离。

2）计算流形邻域中的测地距离矩阵D：令流形分割中初始的测地距离矩阵为d_G（x_i，x_j）=d_E（x_i，x_j），根据最短路径法可以得到邻域拓扑结构G中的x_i，x_j两点的最短距离为d_G（x_i，x_j），于是可得：

$ {d_{ij}}=\left\{ \begin{array}{l} {d_{ij}},\forall {x_j} \in {N_i}or{x_i} \in {N_j}\\ \mathop {\min \left\{ {{d_{ij}},{d_{ik}}+{d_{kj}}} \right\} others} \limits_k。\end{array} \right.$

(1)

从而得到整个流形邻域的测地距离矩阵D。

3）根据多维尺度分析法对X降维，利用矩阵B=HDH实现测地矩阵D的中心化，式中$H=I - \frac{1}{n}L{L^{\text{T}}}$，于是得到矩阵中的元素b_ij：

$ {b_{ij}}={a_{ij}} - \frac{1}{n}\sum\limits_{j=1}^n {{a_{ij}}} - \frac{1}{n}\sum\limits_{i=1}^n {{a_{ij}}}+\frac{1}{{{n^2}}}\sum\limits_{i=1}^n {\sum\limits_{j=1}^n {{a_{ij}}} }。$

(2)

对矩阵B进行基本集分解可得$B \!\!=\!\! HDH \!\!=\!\! X{X^{\text{T}}} \!\!=\!\! L \wedge { \wedge ^{\text{T}}}$，式中$ \wedge=diag\left\{ {{\lambda _1},{\lambda _2},...,{\lambda _d}} \right\}$，矩阵大于0的特征值是d个，分别是${\lambda _1},{\lambda _2},...,{\lambda _d}$，由此可以得到特征值对应的特征向量为Y={y_i}，i=1，2，…，n，那么y_i∈R^d（d < D）是高维数据的低维流形数据^[2]。

在等距离映射中，可以将2个数据间的测地距离为邻域点扩展的近似值。令流形中极为接近的2个高维距离f（y）与降维后的距离f（y^*）满足下式：

$ \mathop {\lim }\limits_{y \to {y^*}} \frac{{\left\| {f(y)- f({y^*})} \right\|}}{{\left\| {y - {y^*}} \right\|}}=1。$

(3)

其中，y，y^*∈R^D。

2 KNN加权近邻分类器

KNN加权是数理统计中的分类算法。令具有n训练样本的训练集为$X=\{({x_i},{l_i}),{x_i} \in {R^d},i=1,2,...,n\} $，且已知任意样本x_i的分类标识为l_i。令待测试样本x_t的分类标识为l_t。加权KNN分类算法的实现思路为：对于测试样本x_t，找到其k个最近邻，然后通过这k个最近邻的分类特点选出测试样本x_t的分类l_t^[3]。通过加权KNN分类使得分类误差M得到最小值，则对于每一个分类l_t∈L，其分类误差M（l_j）是：

$ M({l_j})=\sum\limits_{{l_j} \in L} {P({l_i}\left| {{x_t}} \right.)R({l_i},{l_j})}，$

(4)

其中，P（l_i|x_t）表示测试样本x_t属于l_i的概率，R（l_i，l_j）是属性为l_i的样本分类到l_j中的误差，在KNN加权分类中产生误分类的误差是相同的，即

$ R({l_i},{l_j})=\left\{ \begin{array}{l} 0,i=j，\\ 1,i \ne j。\end{array} \right.$

(5)

因此可得利用KNN加权分类的实现流程

1）计算测试样本x_t与测试集中每个样本x_i间的欧氏距离d（x_t，x_i），即

$ d({x_t},{x_i})={(\sum\limits_{j=1}^d {{{\left\| {{x_{tj}} - {x_{ij}}} \right\|}^2}})^{1/2}}。$

(6)

对距离进行由大到小的排列，找出训练集X中x_t的k+1个近邻样本是${x_{t,1}},{x_{t,2}},...,{x_{t,k+1}}$。

2）令k+1个近邻样本中和x_t距离最大的样本是x_{t, k+1}，其对应距离是d（x_t，x_{t, k+1}），然后用此距离对其余k个距离进行标准化，则

$ D({x_t},{x_i})=\frac{{d({x_t},{x_i})}}{{d({x_t},{x_{t,k+1}})}},i=1,2,...,k。$

(7)

3）在得到标准化的距离D（x_t，x_i）后，根据高斯核函数将此距离转变为x_t和x_i的同胚概率p（x_i|x_t）：

$ p({x_i}\left| {{x_t}} \right.)=\frac{1}{{\sqrt {2\pi } }}\exp \left({ - \frac{{D({x_t},{x_i})}}{2}} \right)。$

(8)

4）根据得到的同胚概率p（x_i|x_t）可以得到x_t属于类别l_i（i=1，2，…，r）的后验概率P（l_i|x_t）：

$ P({l_i}\left| {{x_t}} \right.)=\frac{{\sum\limits_{{x_i} \in X} {\left\{ \begin{array}{l} p({x_i}\left| {{x_t}} \right.),{l_i}={l_t}\\ 0,others \end{array} \right.} }}{{\sum\limits_{{x_i} \in X} {p({x_i}\left| {{x_t}} \right.)} }}。$

(9)

KNN加权算法并不能给出x_t的分类属性值，但是可以得出x_t分类到某一类的分类结果KNN（x_t）：

$ KNN({x_t})=\mathop {\arg \max }\limits_{{l_i} \in L} \left\{ {P({l_i}\left| {{x_t}} \right.)J} \right\}。$

(10)

3 机械旋转故障诊断结果分析

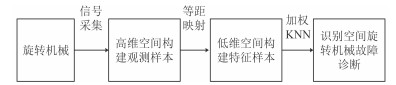
利用等距离映射算法和KNN加权算法进行机械旋转故障诊断的流程如图 1所示。

首先，利用本文所设计的算法将高维空间数据$\{ {x_i}\} _{i=1}^l \subset {R^d}$降维，得到低维特征空间$\{ {y_i}\} _{i=1}^l \subset {R^N}$；其次，根据KNN加权算法对低维训练数据$\{ {y_i},{z_i}\} _{i=1}^l$进行学习，得到分类决策规则；最后对低维测试样本{y_t}进行KNN加权分类。

在进行机械旋转故障诊断时，选择故障特征向量是非常重要的。本文利用经验模式分解法，得到原始机械旋转信号的8个内禀模态分量，然后在时频域中计算其能量，将其作为故障诊断特征。

本文在实验过程中，选取的船舶齿轮箱的输入轴是55个齿轮数，输出的齿轮数量是75，旋转的转速是1 250 r/min，机械的振动信号采样频率是10 kHz。在采用的过程中，根据时间发生的早晚，每9 600个连续采样值形成一个采样单元。在实验过程中分别测了4种情况，如齿轮箱正常运作、齿面磨损、齿根断裂和轴承外圈有损，每种情况得到了60组振动数据。

为了验证本文算法的有效性，本文对经处理的原始振动信号进行了小波去噪、故障特征提取、采用本文算法降维，然后依次是主元分析法、多维尺度法和本文算法进行模式识别，识别结果如表 1所示。

通过表 1的对比可知，正常运作时信号平缓，3种方法都有很优的诊断率，在齿轮断裂中得到的信号特征明显，3种方法识别效果都较好。而其他2种故障特征变化不是很明显，每个状态的边界不明晰，导致识别效果差。本文算法的测地距离有利于变量的稳健估算，从而提高了诊断效果。