随着经济的发展,大宗货物运输量不断地增加,集装箱作为一种最为经济实惠的运输方式得到广泛的使用。集装箱装船顺序是保证货物运输安全、快捷的重要组成部分。在集装箱运输过程中按照一定的顺序将其装载,能够使得船舶装载的货物量增大,并且使得船舶的稳定性增高,降低货场的翻箱情况。
装船顺序问题是近年来的研究热点,Chen等[1]在单个装船问题的0-1顺序模型的基础上研究了特殊集装箱的装船问题。Ambrosino等[2]构建了集装箱装船的约束条件,对特殊集装箱装船算法进行求解。Bortfeldt等[3]通过定点禁忌长度解决了局部最优解的问题。
1 建立模型在装船问题上是将港口货场的集装箱按照一定的顺序搬运到船舶上,在货场中集装箱是按照行、列、层的顺序摆放的,其中重量大、运输路程远的集装箱会放在船舶的最下方,这样可以避免多次翻箱,以此降低运输成本,在这个运输过程尽量减少翻箱,保持处于船舶稳定状态。
为了更好的研究装船问题,本文对所研究的集装箱作出一些假设:
1)集装箱的尺寸都是20尺的箱子。
2)不适用吊桥和集卡进行船舶操作。
3)在装船的集装箱中没有生鲜箱等特殊箱体。
4)在堆场中进对同一行或同一列的集装箱进行翻箱。
在装船模型中令各个变量参数为:
1)堆场中集装箱的数量为n,设In ={1,2,…,n}是指标集。
2)第i个集装箱的质量是mi ,且已知,i∈In 。
3)第i个集装箱到达目的港的时间标号是ui ,且已知,i∈In
4)第i个集装箱在堆场的行列层分别是bi ,li ,hi ,为已知,i∈In 。
5)B,L,H为船舶上所有集装箱的总的行、列和层。
6)第i个集装箱在船上的位置可以表示为Bi ,Hi ,Li ,i∈In 。
7)第i个集装箱的装船时间是ti ,i∈In 。
船舶在没有装船时的中心为船舶的几何中心表示为:
| $ \!\min z = {\left( {\frac{{\sum\limits_{n = 1}^n {{B_i}{m_i}} }}{{\sum\limits_{n = 1}^n {{m_i}} }} - \frac{B}{2}} \right)^2} \!\!+\! {\left( {\frac{{\sum\limits_{n = 1}^n {{L_i}{m_i}} }}{{\sum\limits_{n = 1}^n {{m_i}} }} - \frac{L}{2}} \right)^2} \!\!+\! \frac{{\sum\limits_{n = 1}^n {{H_i}{m_i}} }}{{\sum\limits_{n = 1}^n {{m_i}} }}\text{,} $ | (1) |
通常情况下堆场的集装箱不能摆放的均匀,并且还有重量和航程的原因,所以应减少翻箱,当处于同行、同列、不同层的集装箱,低层的集装箱要先于高层的,那么就会产生翻箱的问题,即
| $ \zeta _{ij}^1 = \left\{ \begin{array}{l} 1 \text{,} ({b_i} = {b_j}) \wedge ({h_i} = {h_j}) \wedge ({t_i} = {t_j})\text{,}\\ 0\text{,} else\text{,} \end{array} \right. $ | (2) |
式中:i ≠j;i,j∈In 。
由此可以得到整个堆场中装船中总的翻箱率为:
| $ {\rho _1} = \frac{{\sum\limits_{i < j} {\zeta _{ij}^1} }}{n}\text{,} $ | (3) |
2个集装箱不能摆放在船舱的同一个位置上,因此:
| $ {({B_i} - {B_j})^2} + {({L_i} - {L_j})^2} + {({H_i} - {H_j})^2} > 0\text{,} $ | (4) |
2个集装箱在装船时要有先后顺序,则:
| $ {t_i} \ne {t_j},i \ne j,\;\;\;\;i,j \in {I_n}\text{,} $ | (5) |
在同一行同一列,不同层的集装箱,会先让下层的集装箱装船,因此:
| $ {t_i} > {t_j} if ({B_i} = {B_j}) \wedge ({L_i} = {L_j}) \wedge ({H_i} = {H_j})\text{,} $ | (6) |
集装箱在装船时,会使重量大的箱体放在下面,于是可得:
| $ {H_i} > {H_j} if ({B_i} = {B_j}) \wedge ({L_i} = {L_j}) \wedge ({m_i} = {m_j})\text{。} $ | (7) |
式中:i ≠j;i,j∈In 。
在卸载的过程中,同行同列,低层的集装箱先到达港口,则需要进行翻箱,因此:
| $ \zeta _{ij}^2 = \left\{ \begin{array}{l} 1 \text{,} ({B_i} = {B_j}) \wedge ({L_i} = {L_j}) \wedge ({H_i} = {H_j}) \wedge ({u_i} = {u_j})\text{,}\\ 0 \text{,} else\text{,} \end{array} \right. $ | (8) |
产生总的翻箱率是:
| $ {\rho _2} = \frac{{\sum\limits_{i < j} {\zeta _{ij}^2} }}{n}\text{,} $ | (9) |
由上述描述可以建立装船顺序整数规划模型为:
| $\begin{split}\\[-12pt] \min \left\{ \begin{array}{l} {f_1} = {\rho _1} + {\rho _2}\\ {f_2} = \min z = {\left( {\frac{{\sum\limits_{n = 1}^n {{B_i}{m_i}} }}{{\sum\limits_{n = 1}^n {{m_i}} }} - \frac{B}{2}} \right)^2} \!+\! {\left( {\frac{{\sum\limits_{n = 1}^n {{L_i}{m_i}} }}{{\sum\limits_{n = 1}^n {{m_i}} }} - \frac{L}{2}} \right)^2}\! +\! \\ \frac{{\sum\limits_{n = 1}^n {{H_i}{m_i}} }}{{\sum\limits_{n = 1}^n {{m_i}} }}\text{。} \end{array} \right. \end{split}$ | (10) |
| $ {\rm {s.t}}. {({B_i} - {B_j})^2} + {({L_i} - {L_j})^2} + {({H_i} - {H_j})^2} > 0\text{,} $ | (11) |
| $ {({t_i} = {t_j})^2} > 0\text{,} $ | (12) |
| $ {t_i} > {t_j} if ({B_i} = {B_j}) \wedge ({L_i} = {L_j}) \wedge ({H_i} > {H_j})\text{,} $ | (13) |
| $ {H_i} > {H_j} if ({B_i} = {B_j}) \wedge ({L_i} = {L_j}) \wedge ({m_i} \le {m_j})\text{,} $ | (14) |
其中:1≤Bi ≤B,1≤Li ≤L,1≤Hi ≤H,1≤ti ≤n;Bi ,Li ,Hi ,ti ∈In 。
2 利用粒子群算法进行集装箱装船顺序本文利用粒子群算法对上述装船顺序整体规划模型进行求解,利用二次平方和加权将原目标函数转化为:
| $ f = {\lambda _1}{({f_1} - 0.3)^2} + {\lambda _2}{({f_2} - 3)^2}\text{。} $ | (15) |
式中:λ1,λ2 > 0,λ1 +λ2=1。翻箱率和稳定性是影响装船顺序的两大因素,本文令λ1=λ2=0.5。
利用粒子算法进行装船顺序求解可以描述为[4]:
1)设定初值bi
,li
,hi
,mi
,ui
(i=1,2,…,n)和B,L,H,以及最大迭代次数是Nmax,种群大小是M,粒子的边界和最小最大速度为
2)种群中M个粒子的初始位置和速度分别是
3)令p:=1,
4)通过bi
,li
,hi
,mi
,可以得到第p个粒子的适应值
5)如果
6)如果p < M,则p:p + 1,执行步骤1。
7)令
8)通过
9)如果k < Nmax,则k:=k + 1,转到步骤3。
将粒子算法应用于本文所建立的装船模型,设定的迭代次数是200次,学习因子都是1.494,粒子数为48,求得的最优适度值是0.368,其粒子最优适度值曲线如图 1所示。
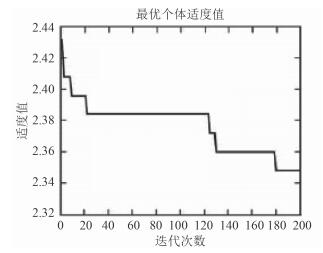
|
图 1 粒子最优适度值曲线 Fig. 1 Particle optimal appropriate value curve |
本文的实验结果可以看出,通过粒子群算法进行装船顺序整体规模,收敛速度快,并且在不断更新粒子位置和速度的过程中,扩大了搜索空间,具有很好的应用效果。
| [1] | CHEN C S, LEE S M, SHEN Q S. An analytical model for the container loading problem[J]. European Journal of Operational Research, 1995, 80 (1): 68–76. DOI: 10.1016/0377-2217(94)00002-T |
| [2] | AMBROSINO D, SCIOMACHEN A, TANFANI E. Stowing a containership:the master bay plan problem[J]. Transportation Research Part A Policy & Practice, 2004, 38 (2): 81–99. |
| [3] | BORTFELDT A, GEHRING H, MACK D. A parallel tabu search algorithm for solving the container loading problem[J]. Parallel Computing, 2003, 29 (5): 641–662. DOI: 10.1016/S0167-8191(03)00047-4 |
| [4] | 潘峰, 陈杰, 甘明刚, 等. 粒子群优化算法模型分析[J]. 自动化学报, 2006, 32 (3): 368–377. |
 2017, Vol. 39
2017, Vol. 39
