舰船电力需求越来越高,迫切需求开发出一款性能稳定,故障率低的船舶电力系统,而在电力系统中,潮流分布常常对整个系统的效能有着非常大的影响[1 -3]。因此本文的主要目标是建立电力系统的最优潮流模型,对其网络结构中的潮流分布和电能传输效率进行研究,从而建立其合理的潮流分布模型。本文从多个角度分析电力系统潮流模型中的非线性规划问题,并通过仿真对问题解的误差进行分析,仿真结果表明,本文提出的潮流优化算法已经达到较为优秀的水平。
1 电力系统最优潮流模型船舶电力系统的最优潮流模型建立过程如下:
1)确定电力系统中所有发电机组的输出功率容量[4];
2)确定系统中用电设备的功率分布;
3)对电力网络分布结构进行建模。
通常所谓的电力系统潮流最优模型,主要是为了实现以下目标:在电力系统的网络结构已经确定的情况下,对每个用电设备的调度策略进行优化;下面建立电力系统的目标函数和约束方程[5 -6]。
由矩阵表示的电力系统目标方程为:
| $ f{(x)_{\min }} = \sum\limits_{i \in {S_G}} {\left( {{a_{2i}}P_{{G_i}}^2 + {a_{1i}}{P_{{G_i}}} + {a_{0i}}} \right)} = {F_{COST}}\text{。} $ | (1) |
式中ai 为电力系统发电机组的消耗系数,注意(i=1,2,0)。
设计系统的潮流方程f(x)满足:
| $ h(x) = {P_G} - {P_D} - e. * (Ge - Bf) - f. * (Gf - Be)\text{,} $ | (2) |
式(2)中的约束条件为:
| $ g(x) = \left[ {\begin{array}{*{20}{c}} {{g_p}}\\ {{g_v}} \end{array}} \right]\text{,} $ | (3) |
式中:gp
=pGI
;I∈SG
;
用矩阵表示为:
| $ J(x) = h{(x)^T} = \left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{{\partial P}}{{\partial {P_G}}}} & {\displaystyle\frac{{\partial P}}{{\partial e}}} & {\displaystyle\frac{{\partial P}}{{\partial f}}} \end{array}} \right]\text{,} $ | (4) |
上式中满足:
| $ \begin{aligned} & \frac{{\partial {P_I}}}{{\partial {P_G}}} = {I_{{n_g}}},I \in {S_G} \text{,}\\ & \frac{{\partial P}}{{\partial e}} = - (EG + FB) - {D_{iag}}\left[ {Ge - Bf} \right] \text{,}\\ & \frac{{\partial P}}{{\partial f}} = - (EB + FG) + {D_{iag}}\left[ {Gf + Be} \right] \text{。} \end{aligned} $ | (5) |
对上述的目标函数求一阶偏导:
| $ \nabla f(x) = \left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{{\partial f(x)}}{{\partial {P_G}}}}\\ \\ {\displaystyle\frac{{\partial f(x)}}{{\partial e}}}\\ \\ {\displaystyle\frac{{\partial f(x)}}{{\partial f}}} \end{array}} \right] \text{,} $ | (6) |
其中:
| $ \begin{array}{l} \displaystyle\frac{{\partial f(x)}}{{\partial {P_G}}} = 2{a_2}. * {P_G} + {a_1} \text{,}\\ \\ \displaystyle\frac{{\partial f(x)}}{{\partial e}} = 2\sum\limits_{} {G. * (\overline E } - \overline E ') \text{,}\\ \displaystyle\frac{{\partial f(x)}}{{\partial f}} = 2\sum\limits_{} {G. * (\overline F } - \overline F ') \text{。} \end{array} $ | (7) |
约束条件为:
| $ \nabla g(x) = \left[ {\begin{array}{*{20}{c}} {{I_{{N_g}}}} & 0 & 0\\ 0 & 0 & {\displaystyle\frac{{\partial {g_v}}}{{\partial e}}}\\ 0 & 0 & {\displaystyle\frac{{\partial {g_v}}}{{\partial f}}} \end{array}} \right] \text{,} $ | (8) |
其中:
| $ \frac{{\partial {g_v}}}{{\partial e}} = 2Diag[e]\;\;\frac{{\partial {g_v}}}{{\partial f}} = 2Diag[f] \text{,} $ | (9) |
对潮流方程进行二阶偏导求解:
| $ \begin{aligned} {\nabla ^2}h(x)y = \left[ {\begin{array}{*{20}{c}} 0 & 0 & 0\\[10pt] 0 & {\displaystyle\frac{{{\partial ^2}h(x)}}{{\partial {e^2}}}y} & {\displaystyle\frac{{{\partial ^2}h(x)}}{{\partial e\partial f}}y}\\[10pt] 0 & {\displaystyle\frac{{{\partial ^2}h(x)}}{{\partial f\partial e}}y} & {\displaystyle\frac{{{\partial ^2}h(x)}}{{{\partial ^{}}{f^2}}}y} \end{array}} \right] \text{,} \end{aligned} $ | (10) |
其中满足:
| $ \begin{aligned} \frac{{{\partial ^2}h(x)}}{{\partial {e^2}}}y = & \frac{{{\partial ^2}h(x)}}{{\partial {f^2}}}y =\\ & - \overline G .*\overline Y + \overline B .*\overline {{Y_N}} + ( - \overline G .*\overline Y + \overline B .*\overline {{Y_N}} )' \text{,}\\ \frac{{{\partial ^2}h(x)}}{{\partial e\partial f}}y = & \left( {\frac{{{\partial ^2}h(x)}}{{\partial f\partial e}}y} \right)' =\\ & (\overline B .*\overline Y + \overline G .*{\overline Y _N}) - (\overline B .*\overline Y + \overline G .*{\overline Y _N})' \text{,}\\ & \overline Y = \left[ {\begin{array}{*{20}{c}} {y1} & \ldots & {y1}\\ \vdots & \ddots & \vdots \\ {{y_N}} & \cdots & {{y_N}} \end{array}} \right] = y(1toN){I_N} \text{。} \end{aligned} $ | (11) |
对电力系统的潮流方程进行非线性求解,从而可以得到一个具有约束条件的解,因此设计如下的数学模型:
| $ \begin{aligned} & \min f(x)\;h(x) = 0\;\;\underline g \leqslant g(x) \leqslant \overline g \text{,}\\ & x \in {R^n},h(x) = \left[ {{h_1}(x), \cdots {h_m}(x)} \right]' \text{,}\\ & g(x) = \left[ {{g_1}(x) \cdots {g_r}(x)} \right]' \text{,}\\ & x \in {R^n},f:{R^n} \to R,h:{R^n} \to {R^m};y \in {R^m} \text{,} \end{aligned} $ | (12) |
通过拉格朗日进行变换:
| $ \begin{aligned} L(x, & l,u,y,z,w,\overline z ,\overline z ) \equiv f(x) - {y^T}h(x) -\\ & {z^T}\left[ {g(x) - l - \underline g } \right] - {w^T}\left[ {g(x) + u - \overline g } \right] - \overline z 'l - \overline w 'u \text{。} \end{aligned} $ | (13) |
式中
通过最优方程的求导,得到:
| $ \left\{ {\begin{array}{*{20}{c}} {\displaystyle\frac{{\partial L(x)}}{{\partial l}} = z - \overline z = 0\text{,}}\\[10pt] {\displaystyle\frac{{\partial L(x)}}{{\partial u}} = - w - \overline w = 0\text{,}} \end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}} {\overline z = z} \text{,}\\ {\overline w = - w} \text{。} \end{array}} \right. $ | (14) |
从而可以得到最优方程解为:
| $ \begin{array}{l} \left\{ {\begin{aligned} & {{L_x} = \nabla f(x) - \nabla h(x)y - \nabla g(x)(z + w) = 0} \text{,}\\ & {{L_y} = h(x) = 0} \text{,}\\ & {{L_z} = g(x) - l - \underline g = 0} \text{,}\\ & {{L_w} = g(x) + u - \overline g = 0} \text{,} \end{aligned}} \right.\\ \\ \left\{ {\begin{array}{*{20}{c}} \!\!\!\!\!{{L_l} = LZe = 0} \text{,}\\ \\ \!\!\!{{L_u} = UWe = 0} \text{。} \end{array}} \right. \end{array} $ | (15) |
式中:
建立船舶电力系统仿真环境,并就上文提出的算法性能进行仿真验证,由于潮流算法中的多数计算步骤都已经转化为线性方程的求导,因此节约了大量的仿真时间,同时该算法的综合性能得到了提高,稳定性也得到了改善。
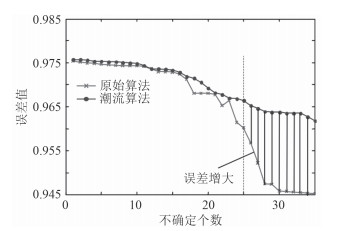
如图 1所示为原始算法和潮流算法的误差仿真结果。当系统的不确定量缓慢增加后,系统的电压输出也会随之降低,当系统的不确定数超过20后,2种算法之间的仿真误差会随之增加;特别是当不确定数达到35以后,两者的误差值已经达到了0.03。从曲线的平滑程度看,潮流算法的整体误差范围更小,系统的稳定性也更好。
|
图 1 误差分析 Fig. 1 Error Analysis |
本文重点研究了船舶电力系统中的潮流分布问题,建立了合理的状态模型,并通过对最优非线性方程组的求解,得到了误差范围可控的分布模型,具有一定的实用价值。
| [1] | 冮明颖, 鲁宝春, 姜丕杰, 等. 基于广义Tellegen定理的小扰动定理在含光伏源的电力系统潮流算法中的应用研究[J]. 电力系统保护与控制, 2015 (18): 31–36. |
| [2] | 刘光梅, 王锡淮, 肖建梅. 基于混合蛙跳算法的舰船电力系统网络重构[J]. 科技风, 2014 (8): 75–76. |
| [3] | 王丛佼, 王锡淮, 肖建梅. 改进差分进化算法在舰船电力系统网络重构中的应用[J]. 船舶工程, 2013 (6): 55–59+67. |
| [4] | SUEYOSHI T, GOTO M. Undesirable congestion under natural disposability and desirable congestion under managerial disposability in U. S. electric power industry measured by DEA environmental assessment[J]. Energy Economics, 2016, 234 : 432–440. |
| [5] | JIANG Ping, MA Xue-jiao. A hybrid forecasting approach applied in the electrical power system based on data preprocessing, optimization and artificial intelligence algorithms[J]. Applied Mathematical Modelling, 2016 (12): 345–350. |
| [6] | Mário César Giacco Ramos, Carlos Márcio Vieira Tahan. An Assessment of the electric power quality and electrical installation impacts on medical electrical equipment operations at health care facilities[J]. American Journal of Applied Sciences, 2009 (64): 65–70. |
 2017, Vol. 39
2017, Vol. 39
