船舶的运动控制一直都是船舶系统中的重中之重,尤其在复杂的海洋环境中,要实现对船舶的航迹控制,必须对控制系统中的各种不确定因素做到非常精确的把握[1-3]。因此本文对船舶运动奇异系统的工作原理进行了研究,并设计了相应的控制器,从内部的稳定度控制和非线性跟踪2个方面对此系统的鲁棒性能展开深入的研究。
1 船舶运动奇异系统控制器的设计本文设计的系统控制器,满足如下的奇异系统:
| $ \begin{array}{l} \mathop E\nolimits_{\sigma (t)} \dot x(t) = \mathop A\nolimits_{\sigma (t)} x(t),\\ x(0) = \mathop x\nolimits_0 。 \end{array} $ | (1) |
上述系统的初始值为
| $ \sigma (t):\mathop R\nolimits^ + \to \{ 1,2,...,p\} , $ | (2) |
上述的转换规则表示的是分段且连续的函数,p为系统交换模式的数量,并且满足i∈{1,2,…,p},Ei和Ai为转换规则中的常数矩阵。
假设运动系统中的阶数表示为Ei=r≤n,采用(Ei,Ai)为第i个子系统的控制状态。设系统的转换常数ti,满足
| $ \begin{array}{l} 0{\rm{ = }}\mathop t\nolimits_0 < \mathop t\nolimits_1 < \ldots < \mathop t\nolimits_i < \mathop t\nolimits_{i + 1} < \ldots ,\\ \sigma (t) = \mathop \sigma \nolimits_i ,t \in [\mathop t\nolimits_i ,\mathop t\nolimits_{i + 1} ),\mathop \sigma \nolimits_i \in \{ 1,2,...,p\} 。 \end{array} $ | (3) |
注意到,σ(t)的平均停留时间为τa,若存在正数N0,需要使Nσ(τ,t)满足
| $ \mathop N\nolimits_\sigma (\tau ,t) \leqslant \mathop N\nolimits_0 + \frac{{t- \tau }}{{\mathop \tau \nolimits_a }},t \geqslant \tau \geqslant 0, $ | (4) |
式中N0为系统的最佳约束距离。
对于系统中的每个i∈{1,2,...,p},船舶运动奇异系统(Ei,Ai)需要满足2个条件:
1)奇异系统中的行列式(sEi-Ai)非0;
2)在行列式sEi-Ai中的多项式与Ei的秩相等。但是,在船舶运动奇异系统中,由于鲁棒性的要求,奇异系统(Ei,Ai)一般为无脉冲的常规控制信号[4]。
对于控制信号矩阵|Ei|=r≤n,系统中必然存在非奇异矩阵Mi和Ni,令(Ei,Ai)的分解形式满足如下形式:
| $ \begin{array}{l} \mathop {\mathit{\boldsymbol{M}}}\nolimits_i \mathop {\mathit{\boldsymbol{E}}}\nolimits_i \mathop {\mathit{\boldsymbol{N}}}\nolimits_i = \left[ {\begin{array}{*{20}{c}} {\mathop I\nolimits_r } & 0\\ 0 & 0 \end{array}} \right] = :\bar {\mathit{\boldsymbol{E}}},\\[10pt] \mathop {\mathit{\boldsymbol{M}}}\nolimits_i \mathop {\mathit{\boldsymbol{A}}}\nolimits_i \mathop {\mathit{\boldsymbol{N}}}\nolimits_i = \left[ {\begin{array}{*{20}{c}} {\mathop A\nolimits_{11} (i)} & {\mathop A\nolimits_{12} (i)}\\ {\mathop A\nolimits_{21} (i)} & {\mathop A\nolimits_{22} (i)} \end{array}} \right] = :\mathop {\bar {\mathit{\boldsymbol{A}}}}\nolimits_i 。\\[10pt] \mathop A\nolimits_{22} (i) \in \mathop R\nolimits^{(n- r) \times (n- r)} \end{array} $ | (5) |
上述的船舶运动奇异系统中,每个部分的转换都是分段且光滑的,因此,在奇异系统中,并不会出现所谓的狄拉克脉冲[5-6]。
假设系统的状态转换方程为:
| $ \bar x(t) = \left[ {\begin{array}{*{20}{c}} {\mathop {\bar x}\nolimits_1 (t)}\\ {\mathop {\bar x}\nolimits_2 (t)} \end{array}} \right] = \mathop N\nolimits_{\mathop \sigma \nolimits_i }^{- 1} x(t),t \in [\mathop t\nolimits_i ,\mathop t\nolimits_{i + 1} ), $ | (6) |
坐标系统下变换为新的形式为:
| $ \begin{array}{*{20}{l}} {{{\bar{\dot{x}}}_1}\left( t \right)= {\rm{ }}{A_{11}}(\sigma (t)){{\bar x}_1}(t) + {\rm{ }}{A_{12}}(\sigma (t)){{\bar x}_2}(t)},\\ {0 = {\rm{ }}{A_{21}}(\sigma (t)){{\bar x}_1}(t) + {\rm{ }}{A_{22}}(\sigma (t)){{\bar x}_2}(t)}。 \end{array} $ | (7) |
建立新的鲁棒时滞系统:
| $ \begin{array}{*{20}{l}} {dx\left( t \right)\!=\![{A_0}x(t) \!+\!{A_1}x(t- \tau )\!+\!{B_0}u(t)\!+\!{G_0}v(t)]dt\!+\!}\\ {[{A_2}x(t)\!+\!{A_3}x(t- \tau )\!+\!{B_1}u(t)\!+\!{G_1}v(t)]d\omega (t)},\\ {z(t)\!=\!Cx(t)\!+\!Du(t)}。 \end{array} $ | (8) |
得到状态反馈控制器状态方程为:
| $ u(t) = Kx(t)。 $ | (9) |
船舶运动系统的奇异系统,其控制器表达式为
| $ u(t) = Kx(t), $ | (10) |
上述的控制器方向在系统的内部随机稳定,此时若v(t)=0,则可能存在某个维数的矩阵X > 0,S > 0,Y满足:
| $ \left[\!\!\!\! {\begin{array}{*{20}{c}} {{A_0}X \!+\! XA_0^{\rm{T}} \!+\! {B_0}Y \!+\! {Y^{\rm{T}}}B_0^{\rm{T}} \!+\! S} \,\,\,\,\, {{A_1}X} \,\,\,\,\, {XA_2^{\rm{T}} \!+\! {Y^{\rm{T}}}B_1^{\rm{T}}}\\[4pt] \quad\quad{XA_1^{\rm{T}}} \quad \quad\quad\quad\quad\quad{- S}\quad\quad {XA_3^{\rm{T}}}\\[3pt] {{A_2}X + {B_1}Y}\quad\quad\quad\quad\quad {{A_3}X} \quad\quad{- X} \end{array}}\!\! \right] < 0。 $ | (11) |
此时的系统也是随机稳定的。
通常,会采用变换矩阵K=YX-1对系统运动的状态反馈控制器进行变换。
2.2 控制器仿真设计反馈控制器方程为:
| $ \tau = \alpha (\dot \theta ,\theta ,\xi ), $ | (12) |
在运动奇异闭环系统中满足:
1)当输入系统的随机扰动处于合理范围内时,此时具备了鲁棒稳定性。
2)对于运动的位置指令θd,船舶的预测跟踪误差为
| $ e(t) = \theta- {\theta _d}, $ | (13) |
并且逐渐接近0。
因此,设计变量参数ji与di,随上述的奇异系统进行非线性补偿:
| $ \tau = J(\theta ){\rm{u}} + f(\theta ,\dot \theta ) + D\dot \theta , $ | (14) |
式中,
| $ \ddot \theta = {\mathit{\boldsymbol{u}}} $ | (15) |
为了能够对运动轨迹进行精确的跟踪,同时误差控制在合理范围内,对系统的状态变量进行优化,得到:
| $ x = {[{\dot \theta _1}\;\;{\dot \theta _2}\;\;{\theta _1}\;\;{\theta _2}]^{\rm{T}}}, $ | (16) |
变换后的状态方程为:
| $ \dot x = {\mathit{\boldsymbol{A}}}x + {\mathit{\boldsymbol{B}}}u。 $ | (17) |
为了克服在建模过程中引入的干扰信号,需要在奇异系统中加入一定的时滞补偿,其输入量的方程表示为:
| $ dx(t)\!=\![{\mathit{\boldsymbol{A}}}x(t)\!+\!{{\mathit{\boldsymbol{A}}}_1}x(t- 1)\!+\!{\mathit{\boldsymbol{B}}}u(t)]dt\!+\!{{\mathit{\boldsymbol{A}}}_2}x(t)d\omega (t), $ | (18) |
仿真时,设计了如下2个子系统进行验证:
| $ \begin{array}{l} \mathop {\mathit{\boldsymbol{E}}}\nolimits_1 = \left[ {\begin{array}{*{20}{c}} 0 & 1 & 0\\ 1 & 0 & 1\\ 0 & 0 & 0 \end{array}} \right],\mathop {\mathit{\boldsymbol{A}}}\nolimits_1 = \left[ {\begin{array}{*{20}{c}} 2 & 1 & 4\\ {- 1} & {- 1} & 1\\ 1 & 0 & 0 \end{array}} \right],\\ \mathop {\mathit{\boldsymbol{E}}}\nolimits_2 = \left[ {\begin{array}{*{20}{c}} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 0 \end{array}} \right],\mathop {\mathit{\boldsymbol{A}}}\nolimits_1 = \left[ {\begin{array}{*{20}{c}} {- 1} & 2 & 0\\ {- 4} & {- 1} & 0\\ 0 & 1 & 1 \end{array}} \right]。 \end{array} $ | (19) |
假设子系统(E1,A1)是不稳定的,而子系统(E2,A2)是稳定的,都满足:
| $ \mathop \lambda \nolimits_1 = \mathop \lambda \nolimits^U = 1\;\;且\;\;\mathop \lambda \nolimits_2 = \mathop \lambda \nolimits^S =- 0.9, $ | (20) |
则可以断定
当设置参数满足λ=0.5,λ*=0.65,发现转换条件
| $ \frac{{\mathop T\nolimits^S (0,t)}}{{\mathop T\nolimits^U (0,t)}} \geqslant \frac{{\mathop \lambda \nolimits^U + \mathop \lambda \nolimits^* }}{{- \mathop \lambda \nolimits^S- \mathop \lambda \nolimits^* }} = 5.7。 $ | (21) |
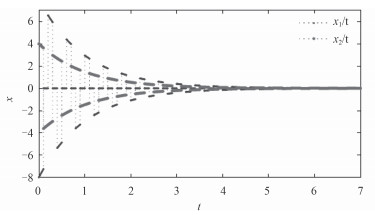
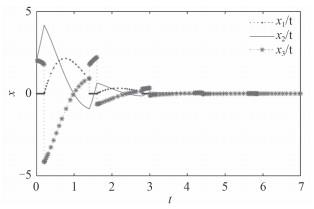
上述的x1,x2状态响应如图 1所示,而加入了干扰信号的x1,x2,x3状态响应如图 2所示。
|
图 1 x1,x2状态响应图 Fig. 1 x1, x2 state response diagram |
|
图 2 x1,x2,x3状态响应图 Fig. 2 x1, x2, x3 state response graphs |
船舶运动控制系统的复杂度决定了其必须具备极高的稳定度,只有这样才会满足人们对航行安全的需求,本文基于奇异系统的控制器,具备了良好的鲁棒H∞性质,仿真结果也满足要求。
| [1] | 彭秀艳, 贾书丽. 船舶横向运动鲁棒PID控制及优化[J]. 控制工程, 2014 (3): 455–458. |
| [2] | 马磊, 张显库. 基于混沌分析的船舶参数激励横摇运动及其减摇鳍控制研究[J]. 船舶力学, 2013 (7): 741–747. |
| [3] | 李红星, 陆安山, 陆益民. 鲁棒滤波在船舶横摇随机控制系统中的应用[J]. 西南大学学报(自然科学版), 2016 (6): 153–158. |
| [4] | 丁福光, 马燕芹, 王元慧, 李江军. 基于状态观测器的多艘船舶鲁棒同步控制[J]. 哈尔滨工程大学学报, 2015 (6): 789–794. |
| [5] | LEE Jae-man, LEE Chun-ju, KIM Young-sik, et al. Determination of global ice loads on the ship using the measured full-scale motion data[J]. International Journal of Naval Architecture and Ocean Engineering, 2016, 453 : 178–182. |
| [6] | WANG Xin, ARAI M. A numerical study on coupled sloshing and ship motions of a liquefied natural gas carrier in regular and irregular waves[J]. Proceedings of the Institution of Mechanical Engineers, 2015, 2291 : 587–590. |
 2017, Vol. 39
2017, Vol. 39
