船舶运动控制技术的发展对人类的航行安全起着非常重要的作用,而智能化的自动控制系统能够极大地提高船舶的控制能力。而船舶在水面航行时,波浪的扰动对船舶的运动有着巨大的影响[1-2]。因此本文重点研究了波浪谱对船舶运动的作用机理,采用了参数控制法,结合各种因素建立了统一的响应方程,极大地提高了船舶运动控制的仿真精度。
1 船舶运动控制方程一般采用非线性模型对船舶的运动状态进行建模研究,通过在模型中充分考虑海洋流体的动力函数,并在X,Y,N坐标系中建立起每个方向状态变量的关系函数,然后计算出其泰勒级数展开式,如下所示:
| $\begin{array}{l} f1(uvr\delta ) = X0 + Xu\Delta u + \frac{1}{2}Xuu\Delta {u^2} + \frac{1}{6}Xuuu\Delta {u^3} + \\ \frac{1}{2}Xvv{v^2} + (\frac{1}{2}Xrr + mXG){r^2} + \frac{1}{2}X\delta \delta {\delta ^2} + \\ \frac{1}{2}Xrru{r^2}\Delta u + \frac{1}{2}Xvvu{v^2}\Delta u + \frac{1}{2}X\delta \delta u{\delta ^2}\Delta u + \\ (Xvr + m)vr + Xv\delta v\delta + Xr\delta r\delta + Xvruvr\Delta u + \\ Xv\delta uv\delta \Delta u + Xr\delta ur\delta \Delta u,\\ f2(uvr\delta ) = Yp0 + Ypou\Delta u + Ypou\Delta {u^2} + Ypouuu\Delta {u^3} + \\ Yvv + \frac{1}{6}Yvvv{v^3} + \frac{1}{2}Yvrrv{r^2} + \frac{1}{2}Yv\delta \delta v{\delta ^2} + Yvuv\Delta u + \\ \frac{1}{2}Yvuuv\Delta {u^2} + (Yr - mu)r + \frac{1}{6}Yrrr{r^3} + \frac{1}{2}Yrvvr{v^2} + \\ \frac{1}{2}Yr\delta \delta r{\delta ^2} + Yrur\Delta u + \frac{1}{2}Yruu。\\ r\Delta {u^2} + Y\delta \delta + \frac{1}{6}Y\delta \delta \delta {\delta ^3} + \\ \frac{1}{2}Y\delta vv\delta {v^2} + \frac{1}{2}Y\delta rr\delta {r^2} + \\ Y\delta u\delta \Delta u + \frac{1}{2}Y\delta uu\delta \Delta {u^2} + Yvr\delta vr\delta + \frac{1}{6}Y\delta \delta \delta u{\delta ^3}\Delta u,\\ f3(uvr\delta ) = Np0 + Npou\Delta u + Ypou\Delta {u^2} + Npouuu\Delta {u^3} + \\ Nvv + \frac{1}{6}Nvvv{v^3} + \frac{1}{2}Nvrrv{r^2} + \frac{1}{2}Nv\delta \delta v{\delta ^2} + Nvuv\Delta u + \\ \frac{1}{2}Nvuuv\Delta {u^2} + (Nr - mxGu)r + \frac{1}{6}Nrrr{r^3} + \frac{1}{2}Nrvvr{v^2} + \\ \frac{1}{2}Nr\delta \delta r{\delta ^2} + Nrur\Delta u + \frac{1}{2}Nruur\Delta {u^2} + N\delta \delta + \frac{1}{6}N\delta \delta \delta {\delta ^3} + \\ \frac{1}{2}N\delta vv\delta {v^2} + \frac{1}{2}N\delta rr\delta {r^2} + N\delta u\delta \Delta u + \frac{1}{2}N\delta uu\delta \Delta {u^2} + \\ Nvr\delta vr\delta + \frac{1}{6}N\delta \delta \delta u{\delta ^3}\Delta u。 \end{array}$ | (1) |
对上述的非线性方程组进行联立求解,得到:
| $\begin{aligned} & \frac{{{\rm{d}}u}}{{{\rm{d}}t}}\!=\!\dot u\!=\!\frac{{f1(u、v、r、\delta )}}{{m - X\mathop {_u}\limits^ \cdot }},\\ & \frac{{{\rm{d}}v}}{{{\rm{d}}t}}\!=\!\dot v\!=\!\frac{{(Iz\!-\!N\mathop {_r}\limits^ \cdot ) \cdot f2(u、v、r、\delta ) \!-\! (mxG - Y\mathop {_r}\limits^ \cdot ) \cdot f3(u、v、r、\delta )}}{{{\rm{(m\!-\!Y}}\mathop {_{\rm{v}}}\limits^ \cdot {\rm{)(Iz - N}}\mathop {_{\rm{r}}}\limits^ \cdot {\rm{) \!-\! (mxG\!-\!N}}\mathop {_{\rm{v}}}\limits^ \cdot {\rm{)(mxG\!-\!Y}}\mathop {_{\rm{r}}}\limits^ \cdot {\rm{)}}}},\!\\ & \frac{{{\rm{d}}v}}{{{\rm{d}}t}}\!=\!\dot r\!=\!\frac{{(m\!-\!Y\mathop {_{\rm{v}}}\limits^ \cdot ) \cdot f3(u、v、r、\delta ) \!-\! (mxG\!-\!N\mathop {_v}\limits^ \cdot ) \cdot f2(u、v、r、\delta )}}{{{\rm{(m\!-\!Y}}\mathop {_{\rm{v}}}\limits^ \cdot {\rm{)(Iz\!-\!N}}\mathop {_{\rm{r}}}\limits^ \cdot {\rm{) \!-\! (mxG\!-\!N}}\mathop {_{\rm{v}}}\limits^ \cdot {\rm{)(mxG\!-\!Y}}\mathop {_{\rm{r}}}\limits^ \cdot {\rm{)}}}}。\! \end{aligned}$ | (2) |
上述3组一阶微分方程可以通过程序进行快速的求解。并得到与时间相关的
| $\begin{array}{l} \mathop {x0}\limits^ \bullet (t) = u(t) \cdot \cos \psi (t) - v(t) \cdot \sin \psi (t),\\ \mathop {y0}\limits^ \bullet (t) = u(t) \cdot \sin \psi (t) + v(t) \cdot \cos \psi (t)。 \end{array}$ | (3) |
积分得到:
| $\begin{array}{l} \psi (t)\!=\!\psi (0)\!+\!\sum\limits_{r = 0}^{t - \Delta t} {r(\tau ) \cdot \Delta t} ,\\ x0(t)\!=\!{x_0}(0)\!+\!\sum\limits_{r = 0}^{t - \Delta t} {\{ u(\tau\!) \cdot \cos\!\psi\!(\tau )\!-\!v(\tau )\sin \psi (\tau )\} } \Delta t,\\ y0(t)\!=\!{y_0}(0)\!+\!\sum\limits_{r = 0}^{t - \Delta t} {\{ u(\tau\!) \cdot \sin\!\psi (\tau )\!+\!v(\tau )\cos \psi (\tau )\} } \Delta t。 \end{array}$ | (4) |
式中:
本文采用了基于概率统计理论的方法对船舶运动时的海洋方向谱进行建模研究[5-6]。下面介绍了一种较为精确的随机波浪力建模方法,即所谓的Jonswap谱,该方向谱模型的建立过程如下:
首先建立时域响应模型
| $\begin{aligned} & {\rm{s}}\left( \omega \right) = \frac{{a{g^2}}}{{{\omega ^5}}}\exp \left[ { - \frac{5}{4}{{\left( {\frac{{{\omega _m}}}{\omega }} \right)}^4}} \right]\gamma ,\\ & a = \exp \left[ { - \frac{{\omega - {\omega _m}}}{{2{\sigma ^2}\omega _m^2}}} \right]。 \end{aligned}$ | (5) |
式中,γ为方向谱峰的升高因子,表达式为
| $\gamma = \frac{{{S_\eta }\left( {{\omega _m}} \right)}}{{{S_\eta }{{\left( {{\omega _m}} \right)}_{{\rm{P - M}}}}}},$ | (6) |
σ为方向谱波峰系数,满足
| $\begin{array}{l} \omega \leqslant {\omega _m}\;\;\;\;\;\;\sigma = 0.07,\\ \omega \geqslant {\omega _m}\;\;\;\;\;\;\sigma = 0.09, \end{array}$ | (7) |
海浪方向谱的波峰频率为:
| ${\omega _m} = 22\frac{g}{{{U_w}}}。$ | (8) |
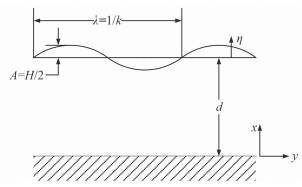
方向谱的模型如图 1所示,图中x轴表示与水面垂直的方向;A表示有关参数,H表示方向谱的波高;k表示波数大小,y轴表示水平面方向;d表示水的深度;λ表示波长;η表示波面的高程。通过对上述变量进行建模,其中的速度势和波面高分别为:
| $\left\{ \begin{array}{l} {\eta _1}\left( {y,t} \right) = A\;\cos \;\psi ,\\ {\phi _1}\left( {x,y,t} \right) = \frac{{A\omega {\rm{ch}}\;kx}}{{k\;{\rm{sh}}\;kd}}\sin \;\psi 。 \end{array}\right.$ | (9) |
式中,λ为波浪谱的圆频率,Ψ=ky -ωt +ε,ε为初相位。当海浪波满足2倍的A时,满足
| ${\omega ^2} = {\rm{g}}k\;{\rm{th}}\;kd,$ | (10) |
相应波速关系式为
| $\left\{ \begin{aligned} & {u_{y1}}\left( {x,y,t} \right) = A\omega \frac{{{\rm{c}}{\rm{h}}kx}}{{{\rm{s}}{\rm{h}}kd}}\cos \psi ,\\ & {u_{x1}}\left( {x,y,t} \right) = A\omega \frac{{{\rm{s}}{\rm{h}}kx}}{{{\rm{s}}{\rm{h}}kd}}\sin \psi 。 \end{aligned} \right.$ | (11) |
式中,uy1和ux1分别为在x轴和y轴方向的速度。
|
图 1 方向谱模型 Fig. 1 Directional spectral model |
下面对波浪方向谱的特性进行仿真,设仿真环境中的水体深度d=500.0 m,波浪的角频率ω分别为0.3、0.4 (rad/s),由上述的方向谱模型可以得到k,并满足Ψ=ky -ωt +ε,设定仿真系统的初相位ε为0。浪的波高分别为H=10 (m)和20 (m)。
下面对
| $\begin{array}{l} {\eta _1}\left( {0,t} \right) = A\cos \psi ,\\ {\eta _1}\left( {y,0} \right) = A\cos \psi 。 \end{array}$ | (12) |
2种环境下的
|
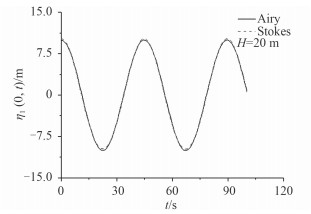
图 2 时域响应曲线 Fig. 2 Time domain response curve |
从上述时域响应曲线可以发现,在不同的波面高程环境中,波浪的角频率状态曲线和理论的预测能够实现良好的吻合。
3 结语本文研究的基于参数法的海浪方向谱预测模型,实现了基本的角频率和波高程的预测功能,同时该模型还能在较少的参数变量环境下,实现较为精确的船舶运动速度预测,具有一定的实用价值。
| [1] | 赵大威, 丁福光, 谢业海, 等. 利用船舶运动数据估计海浪方向谱的研究[J]. 哈尔滨工程大学学报, 2014 (10): 1219–1223. |
| [2] | 杨惠珍, 康凤举, 褚彦军, 等. 基于海浪谱的随机海浪仿真及验证[J]. 系统仿真学报, 2005 (10): 17–19. |
| [3] | 胡渊, 潘皎, 刘彦. 船舶遭遇角频率的估算[J]. 自动化与仪器仪表, 2014 (11): 121–123. |
| [4] | CHARLES MANIÈRE, LISE DURAND, ALICIA WEIBEL, et al. Spark-plasma-sintering and finite element method:From the identification of the sintering parameters of a submicronic α-alumina powder to the development of complex shapes[J]. Acta Materialia, 2016, 102 : 365–370. |
| [5] | LIU Xin-rong, LIU Yong-quan, QU Wan-bo, et al. Internal force calculation and supporting parameters sensitivity analysis of side piles in the subway station excavated by Pile-Beam-Arch method[J]. Tunnelling and Underground Space Technology incorporating Trenchless Technology Research, 2016, 56 : 1432–1436. |
| [6] | ALONSO H, MAGALHÃES H, MENDONÇA T, et al. Multiple strategies for parameter estimation via a hybrid method:a comparative study[J]. IFAC Proceedings Volumes, 2006, 3918 : 760–765. |
 2017, Vol. 39
2017, Vol. 39
