船舶机舱环境监测报警系统是组成船舶自动化的重要部分,现阶段我国拥有较高自动化水平的船舶自动控制和机舱报警系统等,但在火灾预警等方面的自动化研究则相对较浅,导致现有的船舱环境监测系统无法进行及时的火灾预警[1]。传统的船舱测温方式主要是直接测温法,该方法响应时间长,不能及时反映船舱温度的变化规律,而要想达到温度预测,进而进行火警预警,目前采用的方法是基于实验数据和采用线性回归的方法,该方法需要根据大量的实验数据建立模型,使得该方法受到一定的应用限制[2]。
目前应用于环境数据预测方面的研究大多是基于数学模型的建立,而一般基于实验数据的线性回归的温度预测方法需要大量的实验数据来预先建立数学模型,使得该方法受到一定限制。BP 神经网络能通过误差反传误差反向传播算法学习,按照减少目标输出与实际误差的方向,逐层修正输出层与个输出层之间的连接权值,不断完善数学模型,使之实现温度预测的功能[3]。
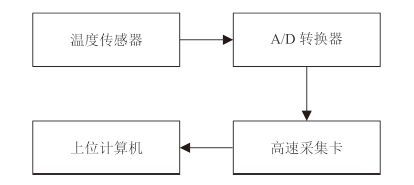
1 基于 BP 神经网络的温度预测方法设计 1.1 现有的船舱环境温度测试方法现有的船舶机舱环境监控测量系统通过温度传感器采集船舱各个位置的温度参数,得到输入模拟量,通过 A/D 转换成为数字信号,接着经高速采集卡采集存储数据,单片机对采集到的温度数据进行分析处理,并将处理所得的实时温度通过显示模块显示(见图 1)。
|
图 1 温度测量原理图 Fig. 1 Schematic diagram of temperature measurement |
现有的船舱环境温度测试方法采用的温度采集方法和数据处理方法较为简单,可以实时显示舱内各位置的温度变化,但是不能起到也测温度变化的功能,无法起到提前预警的作用[4]。
1.2 BP 神经网络在本船舱温度预测模型中,利用 BP 神经网络对温度传感器所测得的温度进行预测的温度预测算法,替代了传统的温度数据处理方法,与传统的温度预测方法相比,减少了大量建模所需的的数据,有明显的优势[5]。
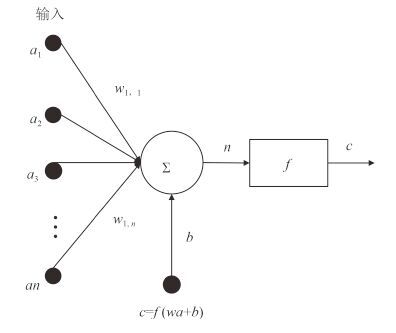
BP 神经网络的拓扑模型包括输入层、隐层和输出层,首先输入样本从输入层单元传到隐含层单元,经隐含层单元处理后产生一个输出,传输至输出层[6](见图 2)。
|
图 2 典型的 BP 神经网络模型 Fig. 2 Typical BP neural network model |
BP 神经网络的基础模型,第 1 层为输入层,中间为隐含层,第T 层为输出层,假设隐含层中的某一层为第t 层,第t 层有p 个神经元,从前 1 层输入到第t 层的第i 个神经元的权值为
| $ \begin{array}{l} y_j^{(t)} = f(\sum\limits_i {w_{ji}^{(t)}} {x_i}-{\theta _j}) = f(ne{t_t})\text{,}\\[10pt] \quad \quad \left( {x_0^{(t-1)} = \theta _i^{(t)},w_{j0}^{(t)} =-1} \right)\text{。} \end{array} $ | (1) |
其中
| $ ne{t_j} = \sum\limits_i {w_{ij}^{(t)}{x_i}-{\theta _j}}\text{,}\;\;\;\left( {i = 1,2, \cdots ,p} \right)\text{,} $ | (2) |
下一节点的输出计算公式如下:
| $ y_j^{(t + 1)} = f(\sum\limits_j {w_{ji}^{(t + 1)}{y_j}-{\theta _1}} ) = f(ne{t_{t + 1}})\text{,} $ | (3) |
其中
| $ ne{t_{t + 1}} = \sum\limits_j {w_{ji}^{(t + 1)}{y_j}-{\theta _1}} \text{。} $ | (4) |
|
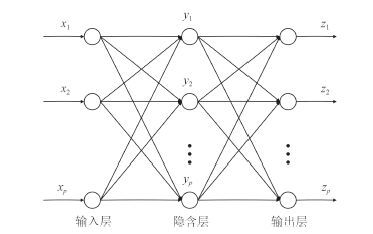
图 3 基于 BP 网络的温度预测模型 Fig. 3 Temperature prediction model based on BP network |
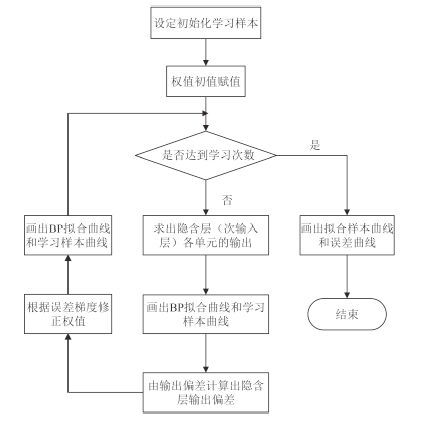
本温度预测模型为 3 层 BP 神经网络,由输入层、隐含层和输出层组成,输入层为单层输入,含a 个神经元,隐含层为单层,神经元个数为b,输出层为单输出,神经元个数为c[8]。本模型选取的学习样本,输入样本点xi(i = 1,2,…,a)为船舱内测得的实时温度数据,隐含层输出节点为yj(j = 1,2,…,b),输出层输出节点为zk(k = 1,2,…,c)。程序流程如图 4 所示。
|
图 4 程序流程图 Fig. 4 Program flow chart |
首先利用传统的温度测试方法测得船舶机舱某个位置的温度值,以获得的温度数据为基础,在 LabVIEW 内建立的 BP 神经网络模型内进行训练。通过温度测量获得一组从无机器运行-主机启动-平稳运行机舱机组工作状态下的温度变化数据。待运行稳定之后获得一组温度数据如表 1,并用传统的线性回归的温度预测方法进行数据预测。
|
|
表 1 实际测量温度 Tab.1 practical measuring temperature |
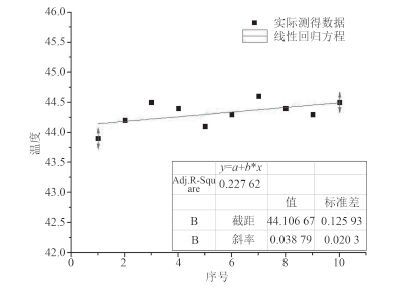
根据已测得的这组温度数据求出线性回归方程(见图 5),利用线性回归方程,得出预测的 10 个温度数据。
|
图 5 线性回归方程 Fig. 5 linear regression equation |
|
|
表 2 预测温度与实际温度 Tab.2 predicted temperature and actual temperature |
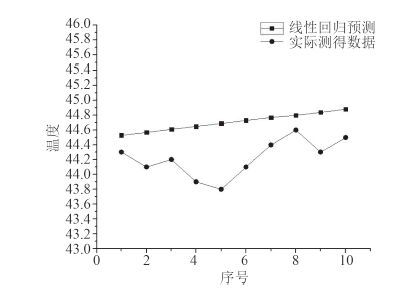
由表 2 中数据比较可知,实时测得的温度数据在某一稳定值附近波动变化,而用线性回归方程预测的温度数据是线性增加的。所以采用线性回归的方法预测温度变化存在一定误差,且与实际情况不符。
|
图 6 预测温度与实际温度比较 Fig. 6 Comparison of predicted temperature and actual temperature |
本文提取表 1 中实际测得的一组温度数据作为训练集,利用表 2 的数据作为测试集。本文构建 3 层 BP 神经网络,由输入层、隐含层和输出层组成,输入层为单层输入,含a 个神经元,隐含层为单层,神经元个数为b,输出层为单输出,神经元个数为c[9]。
本模型选取的学习样本,输入样本点xi(i = 1,2,…,a)为船舱内测得的实时温度数据,隐含层输出节点为yj(j = 1,2,…,b),输出层输出节点为zk(k = 1,2,…,c)。wij(i = 1,2,…,a,j = 1,2,…,b)为输入层到隐层的权值,vjk(j = 1,2,…,b,k = 1,2,…,c)为中间层至输出层的连接权值,相应的,∆wij,∆vjk 分别为wij,vjk 的增量,θj(j = 1,2,…,b)为中间层各单元的输出阈值,γk(k = 1,2,…,c)为输出层各单元的输出阈值。
2.2.2 算法步骤1) 初始化输入数据
由于神经网络的输入要求其输入样本值在 0~1 之间。在网络训练开始之前,首先对直接测得的数据进行归一化处理:
设x’i = 原始的温度数据,xi = 归一化后的数据,(i = 1,2,…,a)。
xi = (x’i-μ)/σ,其中μ 为原始数据的算术平均值,
2) 初始化权值、权值增量和阈值
连接权值wij,vjk 赋予区间(-0.5,0.5)之间的随机数;阈值θj,γk 赋予区间(-1,1)之间的随机值。∆wij = 0,∆vjk = 0(i = 1,2,…,a,j = 1,2,…,b,k = 1,2,…,c)。设置学习率α = 0.075,动态参数η = 0.075。
① 计算隐层输入:
② 计算隐层输出:
yj = (sj-μ)/σ,其中μ 为原始数据的算术平均值,
步骤 2 :根据隐层输出、连接权值vjk 和阈值γk 计算输出层各单元的输入hj,然后利用Lj 计算输出层各单元的输出zk。
① 计算输出层输入:
② 计算输出层输出:
zk = (hk-μ)/σ,其中μ 为原始数据的算术平均值,
步骤 3 :误差估计。
① 根据目标输出值tk 和实际输出zk,计算输出层各单元的一般化误差dk。
| $ {d_k} = ({t_k}-{z_k}) \cdot {z_k}(1-{z_k})\;\;\left( {k = 1,2, \cdots ,c} \right)\text{,} $ | (5) |
② 根据连接权值vjk、输出层的一般化误差dk 和中间层的输出yj 计算中间层各单元的一般化误差ej。
| $ {e_j} = \left[ {\sum\limits_{k = 1}^n {{d_k} \cdot {v_{jk}}} } \right]{y_j}(1-{y_j})\;\;\;\left( {j = 1,2, \cdots ,b} \right)\text{。} $ | (6) |
步骤 4 :
① 根据输出层各单元的一般化误差dk 与中间层各单元输出yj 来计算中间层至输入层的连接权值vjk 的增量 ∆vjk 并修正权值:
| $ \begin{array}{l} \Delta {v_{jk}}\!=\!-\delta {d_k}/\delta \Delta {v_{jk}}\!=\!eta \times \left\{ {\begin{array}{*{20}{l}} {\left[ {{x_i}(i + 1)\!-\!{z_k}} \right] \times {z_k}}\\ { \times (1.0-{z_k}) \times {y_j}} \end{array}} \right\} + \\ \;\;\;\;\;\;\;\;\;\;\; alph\alpha \times \Delta {v_{jk}}\text{。} \end{array} $ | (7) |
② 根据中间层各单元的一般化误差ej 与输入层各单元输入xi 来计算中间层至输入层的连接权值wij 的增量 ∆wij 并修正权值:
| $ \begin{array}{l} \Delta {w_{ij}}\!=\!-\delta {e_j}/\delta \Delta {w_{ij}}\!=\!\eta \times \left\{ {\begin{array}{*{20}{l}} {\left[ {{x_i}(i + 1)-{z_k}} \right] \times {z_k}}\\ { \times (1.0-{z_k}) \times {y_j}}\\ { \times \left[ {1.0-{y_j} \times {x_i}} \right]} \end{array}} \right\} + \\ \;\;\;\;\;\;\;\;\;\;\; alph\alpha \times \Delta {w_{ij}}\text{。} \end{array} $ | (8) |
③ 修正权值:
| $ \begin{array}{l} v{'_{jk}} = {v_{jk}} + \Delta {v_{jk}}\text{;}\\[5pt] w{'_{ij}} = {w_{ij}} + \Delta {w_{ij}}\text{。} \end{array} $ | (9) |
步骤 5 :根据修正的新权值,重新开始循环计算。
3 温度数据分析与预测采用温度测量装置测得的一组轮机平稳运行之后的创藏温度数据作为输入数据,依次从这组输入数据中读取数据,通过建立的神经元模型获得预测温度。将实验所得的预测温度与实际温度比较后计算得到一般化误差,修改权值,重新开始神经网络训练,直到得到期望的温度数据为止[10]。表 3 是一组数据的预测结果。
|
|
表 3 温度预测结果与误差 Tab.3 Results of temperature prediction and error |
|
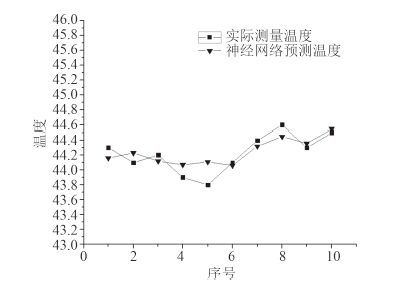
图 7 预测温度与实际测量温度比较 Fig. 7 Comparison between predicted and measured temperature |
实验结果的数据表明,依照上述原理建立的 BP 神经网络,预测得到的温度数据误差较小,平均误差不超过 1%。
4 结 语基于 BP 神经网络建立的温度预测模型具有很好的温度预测效果,当系统运行时,首先由温度测量系统测量一组船舶平稳运行后的温度数据,通过系统分析该组数据得到的船舱预测温度超出正常变化范围时,系统可以提前发出火灾预警。该预测系统的提前预警功能不仅能提高船舱安全性,降低船舱维护成本,减少因为船上火灾带来的损失,提高船舶运营的经济性。
| [1] |
曹玉姣. 船舶机舱自动化监控系统研究[J]. 中国水运, 2010 :107–109.
CAO Yu-jiao. Research on automatic monitoring system of marine engine room[J]. China Water Transport, 2010 :107–109. |
| [2] |
刘跃. 基于. NET的船舶机舱自动化及智能故障诊断技术研究[D]. 镇江:江苏科技大学, 2007:2-8.
LIU Yue. Research on marine engine room automation and intelligent fault diagnosis technology based on. NET[D]. Zhenjiang:Jiangsu University of Science and Technology, 2007:2-8. |
| [3] |
阎平凡, 张长水.
人工神经网络与模拟进化计算[M]. 北京: 清华大学出版社, 2000.
YAN Ping-fan, ZHANG Chang-shui. Artificial neural network and evolutionary computing[M]. Beijing: Tsinghua University Press, 2000. |
| [4] | 孟建伟, 黄学武. 基于CAN总线的船舶机舱综合监控系统[J]. 科技向导, 2012 (8):91–93. |
| [5] |
徐丽娜.
神经网络控制[M]. 哈尔滨: 哈尔滨工业大学出版社, 1999.
XU Li-na. Neural network control[M]. Harbin: Harbin Institute of Technology press, 1999. |
| [6] |
许中华, 杨伟丰, 蒋伟进. BP神经网络学习算法的改进与应用[J]. 计算机工程与科学, 2004, 26 (12):61–6.
XU Zhong-hua, YANG Wei-feng, JIANG Wei-jin. BP neural network learning algorithm improvement and application of[J]. Computer Engineering and Science, 2004, 26 (12):61–6. |
| [7] |
高隽.
人工神经网络原理及仿真实例[M]. 北京: 机械工业出版社, 2003: 49-70.
GAO Jun. Artificial neural network principle and simulation examples[M]. Beijing: Mechanical Industry Press, 2003: 49-70. |
| [8] |
Silnon Haykin著. 叶世伟, 史忠植译. 神经网络原理[M]. 北京:机械工业出版社, 2004, 60-80.
SILNON H, YE Shi-wei, SHI Zhong-zhi, translated. Neural network theory[M]. Beijing:Mechanical Industry Press, 2004, 60-80. |
| [9] | ZHANG Shou-chun, GAO Jun-bo. Design of autopilot steering alarm system on ship based on CAN-bus[C]//International Conference on Electronic and Mechanical Engineering and Information Technology (EMEIT), 2011:4085-4088. |
| [10] |
MARITIN T, HAGAN H B, DEMUTH M B著. 戴葵等译. 神经网络设计[M]. 北京:机械工业出版社, 2005, 30-45.
MARITIN T, HAGAN H B, DEMUTH M B et al. Dai Kui translated. neural network design[M]. Beijing:Mechanical Industry Press, 2005, 30-45. |
 2017, Vol. 39
2017, Vol. 39
